北师大版九年级数学上册 同步练习 1.2 矩形的性质与判定(Word版含答案)
文档属性
| 名称 | 北师大版九年级数学上册 同步练习 1.2 矩形的性质与判定(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 112.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 07:37:00 | ||
图片预览

文档简介
1.2
矩形的性质与判定
一.选择题
1.下列说法中,不正确的是( )
A.四边相等的四边形是菱形
B.同位角相等
C.一组对边平行,另一组对角相等的四边形是平行四边形
D.矩形的对角线相等且互相平分
2.如图,点E与点F是矩形ABCD两条对边AD与BC的中点,分别过点D,B作对角线AC的垂线,垂足为点G,H,顺次连接E,H,F,G,得到四边形EHFG,若AB=4,BC=8,则四边形EHFG的面积是( )
A.
B.8
C.
D.
3.如图,∠BOD=45°,BO=DO,点A在OB上,四边形ABCD是矩形,连接AC、BD交于点E,连接OE交AD于点F.下列4个判断:①OE平分∠BOD;②OF=BD;③DF=AF;④若点G是线段OF的中点,则△AEG为等腰直角三角形.正确判断的个数是( )
A.4
B.3
C.2
D.1
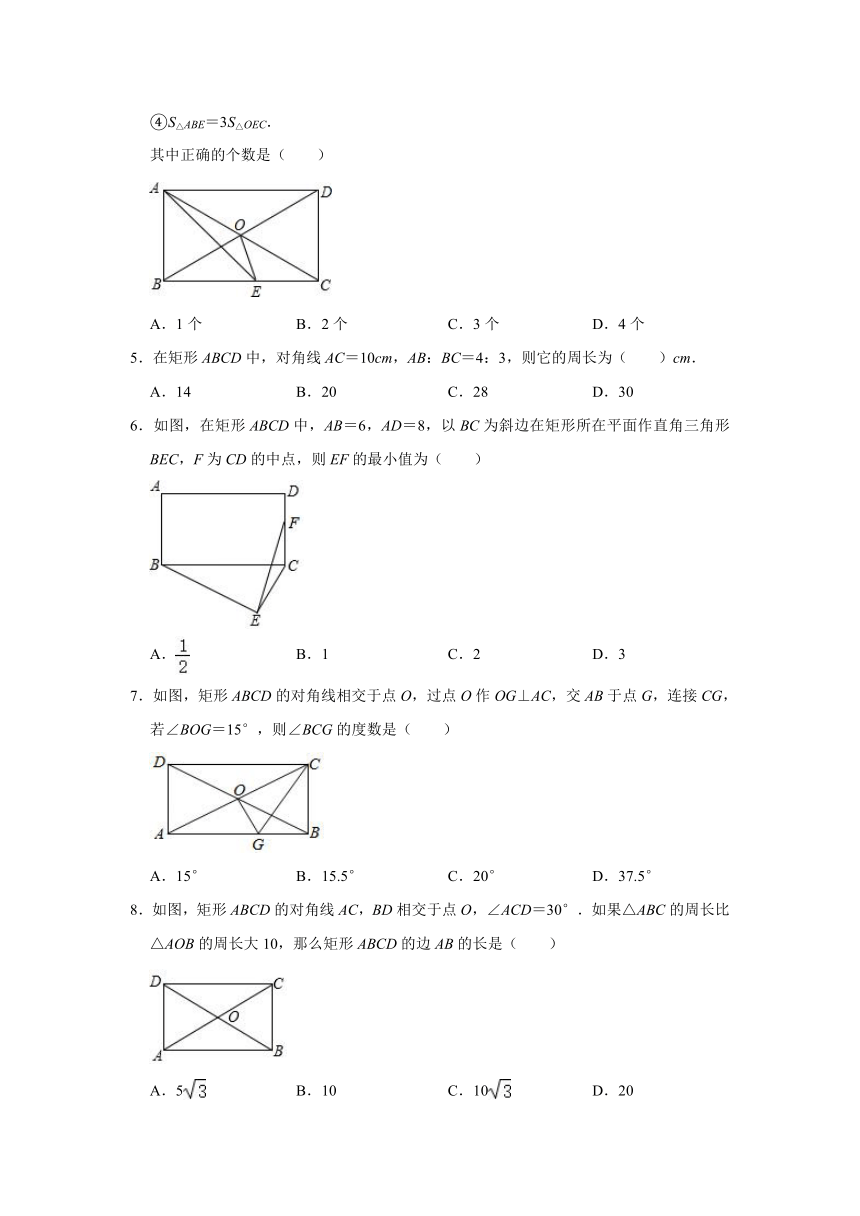
4.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOD=120°,AE平分∠BAD,AE交BC于E.则下列的结论:
①△OBE是等腰三角形;
②BE=2OE;
③∠AEO=30°;
④S△ABE=3S△OEC.
其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
5.在矩形ABCD中,对角线AC=10cm,AB:BC=4:3,则它的周长为( )cm.
A.14
B.20
C.28
D.30
6.如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形所在平面作直角三角形BEC,F为CD的中点,则EF的最小值为( )
A.
B.1
C.2
D.3
7.如图,矩形ABCD的对角线相交于点O,过点O作OG⊥AC,交AB于点G,连接CG,若∠BOG=15°,则∠BCG的度数是( )
A.15°
B.15.5°
C.20°
D.37.5°
8.如图,矩形ABCD的对角线AC,BD相交于点O,∠ACD=30°.如果△ABC的周长比△AOB的周长大10,那么矩形ABCD的边AB的长是( )
A.5
B.10
C.10
D.20
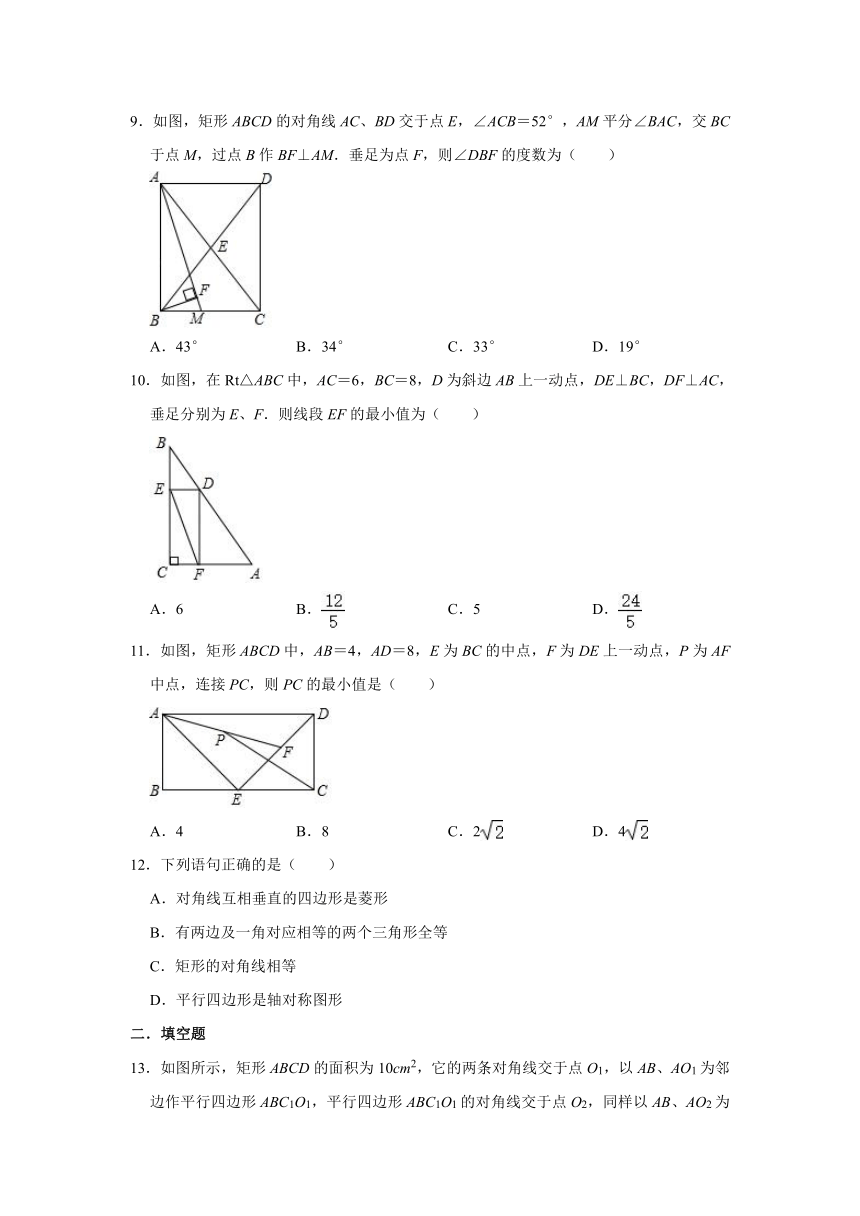
9.如图,矩形ABCD的对角线AC、BD交于点E,∠ACB=52°,AM平分∠BAC,交BC于点M,过点B作BF⊥AM.垂足为点F,则∠DBF的度数为( )
A.43°
B.34°
C.33°
D.19°
10.如图,在Rt△ABC中,AC=6,BC=8,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E、F.则线段EF的最小值为( )
A.6
B.
C.5
D.
11.如图,矩形ABCD中,AB=4,AD=8,E为BC的中点,F为DE上一动点,P为AF中点,连接PC,则PC的最小值是( )
A.4
B.8
C.2
D.4
12.下列语句正确的是( )
A.对角线互相垂直的四边形是菱形
B.有两边及一角对应相等的两个三角形全等
C.矩形的对角线相等
D.平行四边形是轴对称图形
二.填空题
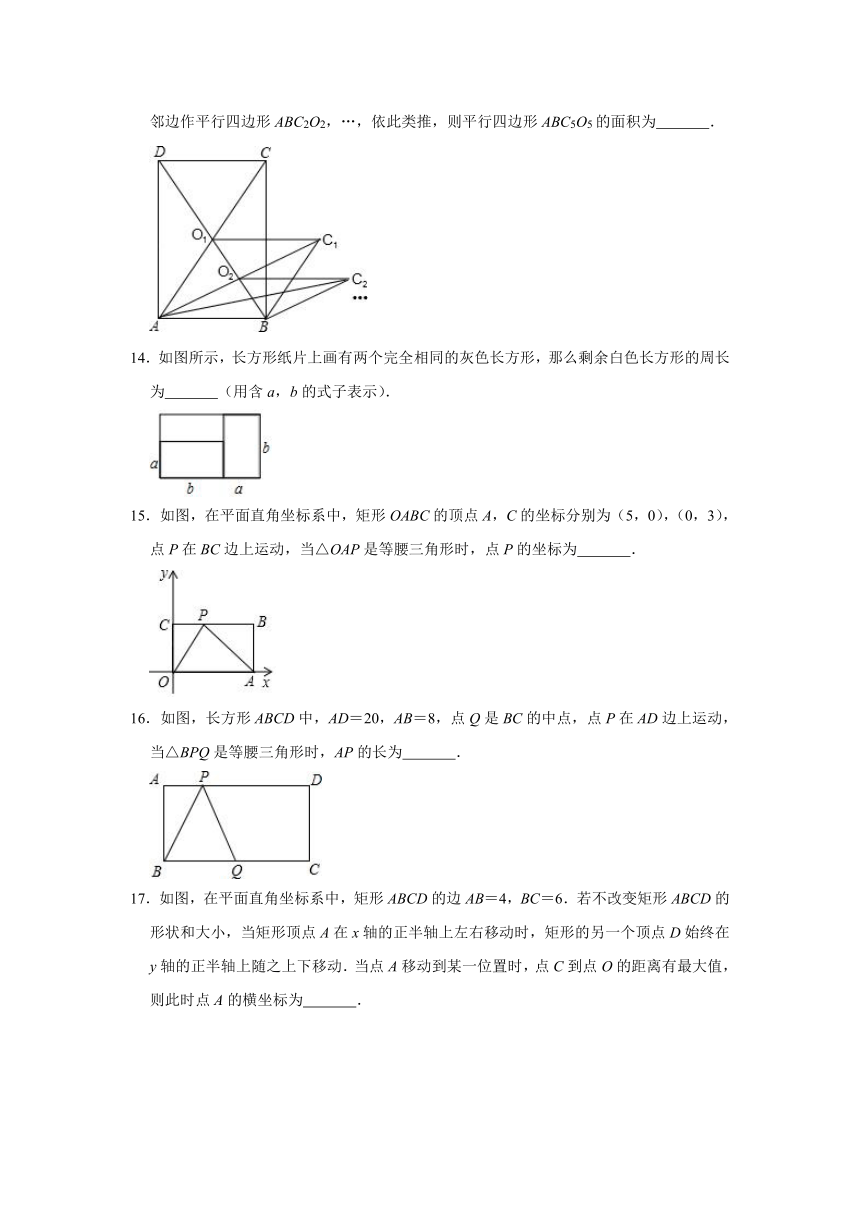
13.如图所示,矩形ABCD的面积为10cm2,它的两条对角线交于点O1,以AB、AO1为邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABC5O5的面积为
.
14.如图所示,长方形纸片上画有两个完全相同的灰色长方形,那么剩余白色长方形的周长为
(用含a,b的式子表示).
15.如图,在平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为(5,0),(0,3),点P在BC边上运动,当△OAP是等腰三角形时,点P的坐标为
.
16.如图,长方形ABCD中,AD=20,AB=8,点Q是BC的中点,点P在AD边上运动,当△BPQ是等腰三角形时,AP的长为
.
17.如图,在平面直角坐标系中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.当点A移动到某一位置时,点C到点O的距离有最大值,则此时点A的横坐标为
.
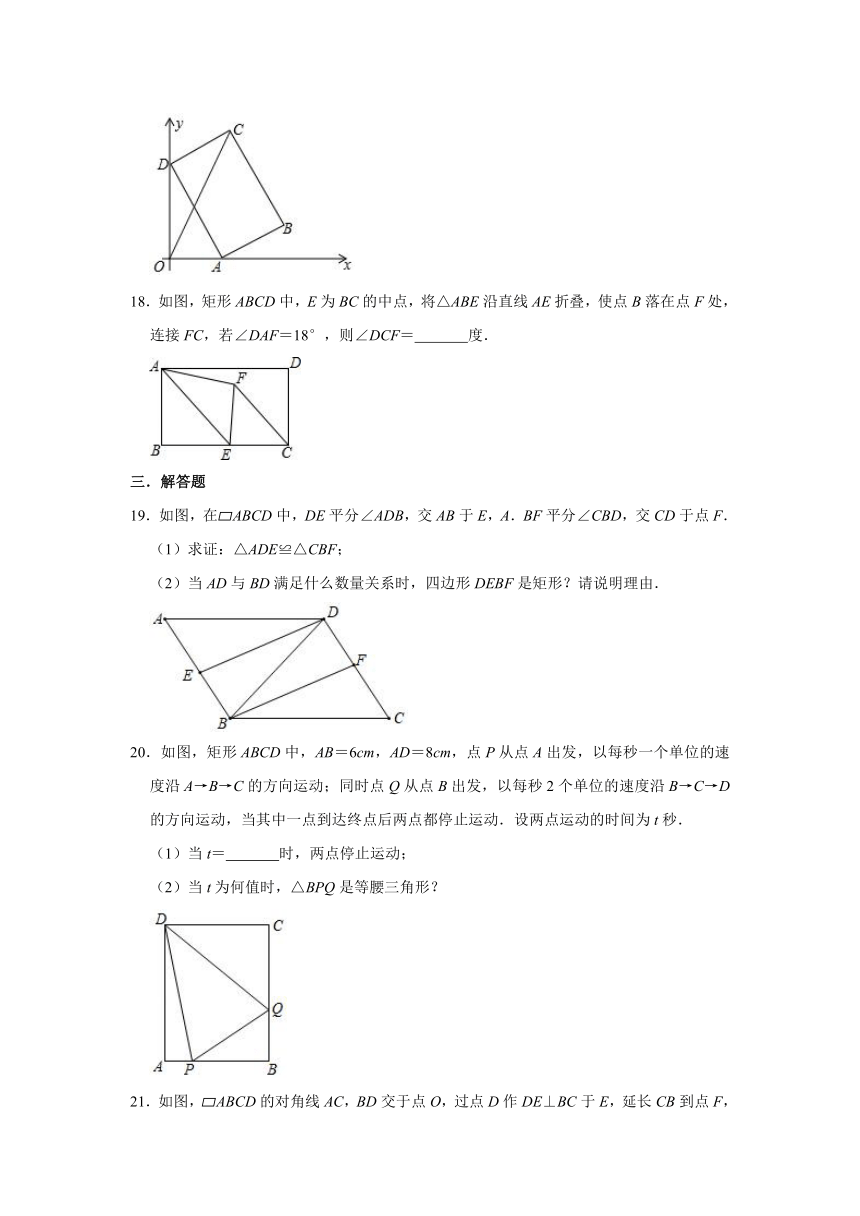
18.如图,矩形ABCD中,E为BC的中点,将△ABE沿直线AE折叠,使点B落在点F处,连接FC,若∠DAF=18°,则∠DCF=
度.
三.解答题
19.如图,在?ABCD中,DE平分∠ADB,交AB于E,A.BF平分∠CBD,交CD于点F.
(1)求证:△ADE≌△CBF;
(2)当AD与BD满足什么数量关系时,四边形DEBF是矩形?请说明理由.
20.如图,矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发,以每秒一个单位的速度沿A→B→C的方向运动;同时点Q从点B出发,以每秒2个单位的速度沿B→C→D的方向运动,当其中一点到达终点后两点都停止运动.设两点运动的时间为t秒.
(1)当t=
时,两点停止运动;
(2)当t为何值时,△BPQ是等腰三角形?
21.如图,?ABCD的对角线AC,BD交于点O,过点D作DE⊥BC于E,延长CB到点F,使BF=CE,连接AF,OF.
(1)求证:四边形AFED是矩形.
(2)若AD=7,BE=2,∠ABF=45°,试求OF的长.
22.如图,在平行四边形ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形.
(2)若AB=14,DE=8,求BE的长.
参考答案
一.选择题
1.
B
2.D.
3.
A.
4.
B.
5.
C.
6.
B.
7.
A.
8.
C.
9.
C.
10.
D.
11.
D.
12.
C.
二.填空题
13.
0.3125cm2.
14.
4b﹣2a.
15.(,3)或(4,3)或(1,3).
16.
4或5或6或16.
17.
.
18.
36.
三.解答题
19.(1)证明:在?ABCD中,AD∥BC,AD=BC,∠A=∠C,
∴∠ADB=∠CBD,
∵DE平分∠ADB,BF平分∠CBD,
∴∠ADE=∠FBC,
在△ADE和△CBF中,,
∴△ADE≌△CBF(ASA);
(2)解:AD=BD,四边形DEBF是矩形.理由如下:
∵△ADE≌△CBF,
∴DE=BF,AE=CF,
又∵AB=CD,
∴BE=DF,
∴四边形DEBF是平行四边形,
∵AD=BD,DE平分∠ADB,
∴DE⊥AB,
∴平行四边形ABCD是矩形.
20.解:(1)∵四边形ABCD是矩形,
∴CD=AB=6,BC=AD=8,
∴AB+BC=BC+CD=14,
∵14÷2=7,
∴t=7;
故答案为:7;
(2)由题意得:AP=t,BQ=2t,
分情况讨论:
当0<t≤4时,若BP=BQ,则6﹣t=2t,
∴t=2;
当4<t≤6时,
若PQ=BQ,则PB=2CQ,6﹣t=2(2t﹣8),
∴t=;
当6<t<7时,由题意可知不存在;
综上所述,当t为2或时,△BPQ是等腰三角形.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵BF=CE,
∴FE=BC,
∴四边形AFED是平行四边形,
∵DE⊥BC,
∴∠DEF=90°,
∴四边形AFED是矩形.
(2)解:由(1)得:∠AFE=90°,FE=AD,
∵AD=7,BE=2,
∴FE=7,
∴FB=FE﹣BE=5,
∴CE=BF=5,
∴FC=FE+CE=7+5=12,
∵∠ABF=45°,
∴△ABF是等腰直角三角形,
∴AF=FB=5,
在Rt△AFC中,由勾股定理得:AC===13,
∵四边形ABCD是平行四边形,
∴OA=OC,
∴OF=AC=.
22.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAF=∠F.
∵∠F=45°,
∴∠DAE=45°.
∵AF是∠BAD的平分线,
∴∠EAB=∠DAE=45°.
∴∠DAB=90°.
又∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
(2)∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠DCB=∠D=90°.
∵AB=14,DE=8,
∴CE=6.
在Rt△ADE中,∠DAE=45°,
∴∠DEA=∠DAE=45°.
∴AD=DE=8.
∴BC=8.
在Rt△BCE中,由勾股定理得:
矩形的性质与判定
一.选择题
1.下列说法中,不正确的是( )
A.四边相等的四边形是菱形
B.同位角相等
C.一组对边平行,另一组对角相等的四边形是平行四边形
D.矩形的对角线相等且互相平分
2.如图,点E与点F是矩形ABCD两条对边AD与BC的中点,分别过点D,B作对角线AC的垂线,垂足为点G,H,顺次连接E,H,F,G,得到四边形EHFG,若AB=4,BC=8,则四边形EHFG的面积是( )
A.
B.8
C.
D.
3.如图,∠BOD=45°,BO=DO,点A在OB上,四边形ABCD是矩形,连接AC、BD交于点E,连接OE交AD于点F.下列4个判断:①OE平分∠BOD;②OF=BD;③DF=AF;④若点G是线段OF的中点,则△AEG为等腰直角三角形.正确判断的个数是( )
A.4
B.3
C.2
D.1
4.如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOD=120°,AE平分∠BAD,AE交BC于E.则下列的结论:
①△OBE是等腰三角形;
②BE=2OE;
③∠AEO=30°;
④S△ABE=3S△OEC.
其中正确的个数是( )
A.1个
B.2个
C.3个
D.4个
5.在矩形ABCD中,对角线AC=10cm,AB:BC=4:3,则它的周长为( )cm.
A.14
B.20
C.28
D.30
6.如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形所在平面作直角三角形BEC,F为CD的中点,则EF的最小值为( )
A.
B.1
C.2
D.3
7.如图,矩形ABCD的对角线相交于点O,过点O作OG⊥AC,交AB于点G,连接CG,若∠BOG=15°,则∠BCG的度数是( )
A.15°
B.15.5°
C.20°
D.37.5°
8.如图,矩形ABCD的对角线AC,BD相交于点O,∠ACD=30°.如果△ABC的周长比△AOB的周长大10,那么矩形ABCD的边AB的长是( )
A.5
B.10
C.10
D.20
9.如图,矩形ABCD的对角线AC、BD交于点E,∠ACB=52°,AM平分∠BAC,交BC于点M,过点B作BF⊥AM.垂足为点F,则∠DBF的度数为( )
A.43°
B.34°
C.33°
D.19°
10.如图,在Rt△ABC中,AC=6,BC=8,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E、F.则线段EF的最小值为( )
A.6
B.
C.5
D.
11.如图,矩形ABCD中,AB=4,AD=8,E为BC的中点,F为DE上一动点,P为AF中点,连接PC,则PC的最小值是( )
A.4
B.8
C.2
D.4
12.下列语句正确的是( )
A.对角线互相垂直的四边形是菱形
B.有两边及一角对应相等的两个三角形全等
C.矩形的对角线相等
D.平行四边形是轴对称图形
二.填空题
13.如图所示,矩形ABCD的面积为10cm2,它的两条对角线交于点O1,以AB、AO1为邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABC5O5的面积为
.
14.如图所示,长方形纸片上画有两个完全相同的灰色长方形,那么剩余白色长方形的周长为
(用含a,b的式子表示).
15.如图,在平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为(5,0),(0,3),点P在BC边上运动,当△OAP是等腰三角形时,点P的坐标为
.
16.如图,长方形ABCD中,AD=20,AB=8,点Q是BC的中点,点P在AD边上运动,当△BPQ是等腰三角形时,AP的长为
.
17.如图,在平面直角坐标系中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.当点A移动到某一位置时,点C到点O的距离有最大值,则此时点A的横坐标为
.
18.如图,矩形ABCD中,E为BC的中点,将△ABE沿直线AE折叠,使点B落在点F处,连接FC,若∠DAF=18°,则∠DCF=
度.
三.解答题
19.如图,在?ABCD中,DE平分∠ADB,交AB于E,A.BF平分∠CBD,交CD于点F.
(1)求证:△ADE≌△CBF;
(2)当AD与BD满足什么数量关系时,四边形DEBF是矩形?请说明理由.
20.如图,矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发,以每秒一个单位的速度沿A→B→C的方向运动;同时点Q从点B出发,以每秒2个单位的速度沿B→C→D的方向运动,当其中一点到达终点后两点都停止运动.设两点运动的时间为t秒.
(1)当t=
时,两点停止运动;
(2)当t为何值时,△BPQ是等腰三角形?
21.如图,?ABCD的对角线AC,BD交于点O,过点D作DE⊥BC于E,延长CB到点F,使BF=CE,连接AF,OF.
(1)求证:四边形AFED是矩形.
(2)若AD=7,BE=2,∠ABF=45°,试求OF的长.
22.如图,在平行四边形ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形.
(2)若AB=14,DE=8,求BE的长.
参考答案
一.选择题
1.
B
2.D.
3.
A.
4.
B.
5.
C.
6.
B.
7.
A.
8.
C.
9.
C.
10.
D.
11.
D.
12.
C.
二.填空题
13.
0.3125cm2.
14.
4b﹣2a.
15.(,3)或(4,3)或(1,3).
16.
4或5或6或16.
17.
.
18.
36.
三.解答题
19.(1)证明:在?ABCD中,AD∥BC,AD=BC,∠A=∠C,
∴∠ADB=∠CBD,
∵DE平分∠ADB,BF平分∠CBD,
∴∠ADE=∠FBC,
在△ADE和△CBF中,,
∴△ADE≌△CBF(ASA);
(2)解:AD=BD,四边形DEBF是矩形.理由如下:
∵△ADE≌△CBF,
∴DE=BF,AE=CF,
又∵AB=CD,
∴BE=DF,
∴四边形DEBF是平行四边形,
∵AD=BD,DE平分∠ADB,
∴DE⊥AB,
∴平行四边形ABCD是矩形.
20.解:(1)∵四边形ABCD是矩形,
∴CD=AB=6,BC=AD=8,
∴AB+BC=BC+CD=14,
∵14÷2=7,
∴t=7;
故答案为:7;
(2)由题意得:AP=t,BQ=2t,
分情况讨论:
当0<t≤4时,若BP=BQ,则6﹣t=2t,
∴t=2;
当4<t≤6时,
若PQ=BQ,则PB=2CQ,6﹣t=2(2t﹣8),
∴t=;
当6<t<7时,由题意可知不存在;
综上所述,当t为2或时,△BPQ是等腰三角形.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵BF=CE,
∴FE=BC,
∴四边形AFED是平行四边形,
∵DE⊥BC,
∴∠DEF=90°,
∴四边形AFED是矩形.
(2)解:由(1)得:∠AFE=90°,FE=AD,
∵AD=7,BE=2,
∴FE=7,
∴FB=FE﹣BE=5,
∴CE=BF=5,
∴FC=FE+CE=7+5=12,
∵∠ABF=45°,
∴△ABF是等腰直角三角形,
∴AF=FB=5,
在Rt△AFC中,由勾股定理得:AC===13,
∵四边形ABCD是平行四边形,
∴OA=OC,
∴OF=AC=.
22.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAF=∠F.
∵∠F=45°,
∴∠DAE=45°.
∵AF是∠BAD的平分线,
∴∠EAB=∠DAE=45°.
∴∠DAB=90°.
又∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
(2)∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠DCB=∠D=90°.
∵AB=14,DE=8,
∴CE=6.
在Rt△ADE中,∠DAE=45°,
∴∠DEA=∠DAE=45°.
∴AD=DE=8.
∴BC=8.
在Rt△BCE中,由勾股定理得:
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
