人教版九年级上册数学 22.1.1 二次函数(解析式的求法)课件(17张)
文档属性
| 名称 | 人教版九年级上册数学 22.1.1 二次函数(解析式的求法)课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 93.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
二次函数解析式的求法
二次函数解析(常见的三种表示形式)
(1)一般式
(2)顶点式
(3)交点式
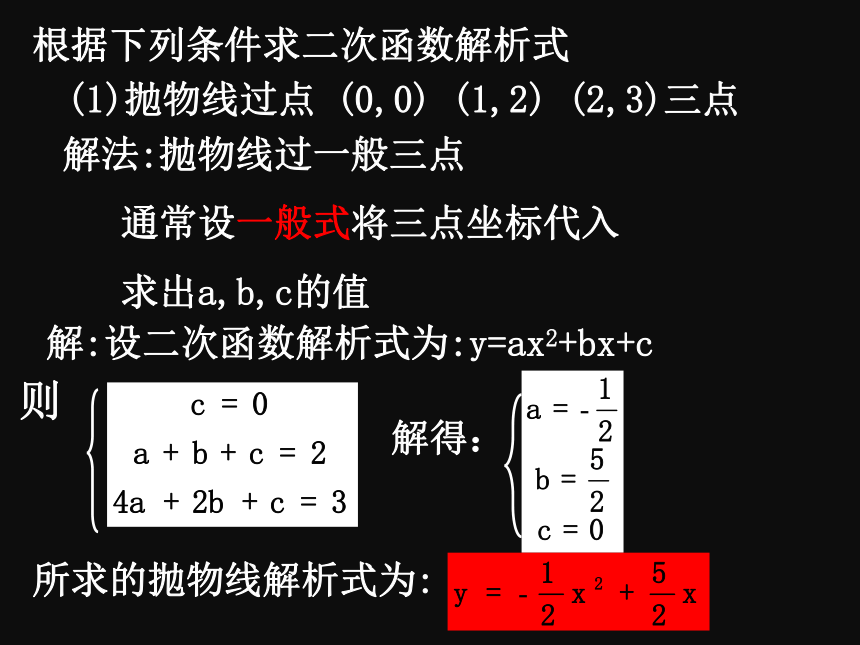
根据下列条件求二次函数解析式
(1)抛物线过点
(0,0)
(1,2)
(2,3)三点
解法:抛物线过一般三点
通常设一般式将三点坐标代入
求出a,b,c的值
解:设二次函数解析式为:y=ax2+bx+c
则
解得:
所求的抛物线解析式为:
(2)抛物线顶点是(2,-1)且过点(-1,2)
解法(一)可设一般式列方程组求a,b,c
解法(二)可设
解:∵抛物线的顶点为(2,-1)
∴设解析式为:y=a(x-2)2-1
把点(-1,2)代入
a(-1-2)2-1=2
顶点式
(3)图象与X轴交于(2,0)
(-1,0)且过点(0,-2)
解法(一)可设一般式
解法(二)可设
解:∵抛物线与X轴交于点(2,0)(-1,0)
∴设解析式为:y=a(x-2)(x+1)
把点(0,-2)代入
a(0-2)(0+1)=-2
解得
a=1
∴y=(x-2)(x+1)
即:y=x2-x-2
交点式
另一些例题讲解:
1.若抛物线y=x2-4x+c
(1)过点A(1,3),求c;
(2)顶点在x轴上,求c。
解:(1)∵A点在抛物线上,将A(1,3)代入解析式
求得
c=6
(2)x轴上的点的特点
(x,0)
根据顶点的纵坐标为0求得:c=4
2.若抛物线
y=ax2+2x+c的对称轴是直线
x=2,且函数的最大值是
-3,求
a,c
分析:由题意知道顶点坐标(2,-3)且为最高点,抛物线开口向下,∴a<0
解:
解得
3.图象与x轴交于(2,0)(3,0)且函数最小值是-3
分析:函数最小值:-3即顶点纵坐标,但隐藏着抛物线开口向上这个条件
可设一般式来解.但比较繁琐
可设交点式来解
求得的解析式为:y=12x2-60x+72
4,练习:求下列二次函数解析式
(1)抛物线
y=x2-5(m+1)x+2m的对称轴是y轴
所求的解析式为:y=x2-2
(2)y=(m-3)x2+mx+m+3的最大值是0
(3)y=ax2+bx+c且a:b:c=2:3:4,函数有最
小值
解得:y=4x2+6x+8
(4)抛物线y=ax2+bx+c的顶点是(-1,2),且a+b+c+2=0
5,思考题:(求下列二次函数解析式)
(1)若抛物线y=(m2-2)x2-4mx+n对称轴是
直线x=2,且最高点在直线
上。
上
解法:可先求出顶点坐标(2,2)
再由题意得
解得:
m=-1
n=-2
即:y=-x2+4x-2
(2)若抛物线y=2x2+bx+c过点(2,3)
且顶点在直线y=3x-2上
解法:可抓住顶点在直线y=3x-2上
设抛物线的顶点坐标为(m,3m-2)来解
所求得的抛物线解析式为:
6.
(1)抛物线y=ax2+bx+c与y=-x2形状相同,对称轴是直线x=3,
最高点在直线y=x+1上,求抛物线解析式;
(2)若(1)中求得的抛物线的顶点在直线y=x+1上移动到点P时,它与x轴交于(x1,0)(x2,0),且x12+x22=6,求P点坐标。
(1)
y=-(x-3)2+4
(2)①
y=-x2+2x+1
P(1,2)
②y=-x2-4x-5
P(-2,-1)【∵△﹤0,∴舍去】
7.已知直线y=kx+b与x轴相交于点A的横坐标为2,与抛物线y=ax2相交于B、C两点,且点B与点P(-1,1)关于y轴对称。
(1)求直线和抛物线的解析式;
(2)若抛物线上有一点D,使S△AOD
=S△BOC,求点D的坐标。
8
已知抛物线
y=ax2+bx+c
与直线y=kx+4
相交于点A(1,m),B(4,8),与x轴交于坐标原点O和点C.
(1)求直线和抛物线解析式.
(2)在x轴上方的抛物线是否存在D点,使得S△OCD
=S△OCB.若存在,求出所有符合条件的点;若不存在,说明理由。
已知当x=-1时,抛物线最高点的纵坐标为4,且与x轴两交点之间的距离为6,求此函数的解析式。
x
y
O
x=-1
小结(1)二次函数解析式的三种表示形式
(1)一般式
(2)顶点式
(3)交点式
二次函数解析式的求法
二次函数解析(常见的三种表示形式)
(1)一般式
(2)顶点式
(3)交点式
根据下列条件求二次函数解析式
(1)抛物线过点
(0,0)
(1,2)
(2,3)三点
解法:抛物线过一般三点
通常设一般式将三点坐标代入
求出a,b,c的值
解:设二次函数解析式为:y=ax2+bx+c
则
解得:
所求的抛物线解析式为:
(2)抛物线顶点是(2,-1)且过点(-1,2)
解法(一)可设一般式列方程组求a,b,c
解法(二)可设
解:∵抛物线的顶点为(2,-1)
∴设解析式为:y=a(x-2)2-1
把点(-1,2)代入
a(-1-2)2-1=2
顶点式
(3)图象与X轴交于(2,0)
(-1,0)且过点(0,-2)
解法(一)可设一般式
解法(二)可设
解:∵抛物线与X轴交于点(2,0)(-1,0)
∴设解析式为:y=a(x-2)(x+1)
把点(0,-2)代入
a(0-2)(0+1)=-2
解得
a=1
∴y=(x-2)(x+1)
即:y=x2-x-2
交点式
另一些例题讲解:
1.若抛物线y=x2-4x+c
(1)过点A(1,3),求c;
(2)顶点在x轴上,求c。
解:(1)∵A点在抛物线上,将A(1,3)代入解析式
求得
c=6
(2)x轴上的点的特点
(x,0)
根据顶点的纵坐标为0求得:c=4
2.若抛物线
y=ax2+2x+c的对称轴是直线
x=2,且函数的最大值是
-3,求
a,c
分析:由题意知道顶点坐标(2,-3)且为最高点,抛物线开口向下,∴a<0
解:
解得
3.图象与x轴交于(2,0)(3,0)且函数最小值是-3
分析:函数最小值:-3即顶点纵坐标,但隐藏着抛物线开口向上这个条件
可设一般式来解.但比较繁琐
可设交点式来解
求得的解析式为:y=12x2-60x+72
4,练习:求下列二次函数解析式
(1)抛物线
y=x2-5(m+1)x+2m的对称轴是y轴
所求的解析式为:y=x2-2
(2)y=(m-3)x2+mx+m+3的最大值是0
(3)y=ax2+bx+c且a:b:c=2:3:4,函数有最
小值
解得:y=4x2+6x+8
(4)抛物线y=ax2+bx+c的顶点是(-1,2),且a+b+c+2=0
5,思考题:(求下列二次函数解析式)
(1)若抛物线y=(m2-2)x2-4mx+n对称轴是
直线x=2,且最高点在直线
上。
上
解法:可先求出顶点坐标(2,2)
再由题意得
解得:
m=-1
n=-2
即:y=-x2+4x-2
(2)若抛物线y=2x2+bx+c过点(2,3)
且顶点在直线y=3x-2上
解法:可抓住顶点在直线y=3x-2上
设抛物线的顶点坐标为(m,3m-2)来解
所求得的抛物线解析式为:
6.
(1)抛物线y=ax2+bx+c与y=-x2形状相同,对称轴是直线x=3,
最高点在直线y=x+1上,求抛物线解析式;
(2)若(1)中求得的抛物线的顶点在直线y=x+1上移动到点P时,它与x轴交于(x1,0)(x2,0),且x12+x22=6,求P点坐标。
(1)
y=-(x-3)2+4
(2)①
y=-x2+2x+1
P(1,2)
②y=-x2-4x-5
P(-2,-1)【∵△﹤0,∴舍去】
7.已知直线y=kx+b与x轴相交于点A的横坐标为2,与抛物线y=ax2相交于B、C两点,且点B与点P(-1,1)关于y轴对称。
(1)求直线和抛物线的解析式;
(2)若抛物线上有一点D,使S△AOD
=S△BOC,求点D的坐标。
8
已知抛物线
y=ax2+bx+c
与直线y=kx+4
相交于点A(1,m),B(4,8),与x轴交于坐标原点O和点C.
(1)求直线和抛物线解析式.
(2)在x轴上方的抛物线是否存在D点,使得S△OCD
=S△OCB.若存在,求出所有符合条件的点;若不存在,说明理由。
已知当x=-1时,抛物线最高点的纵坐标为4,且与x轴两交点之间的距离为6,求此函数的解析式。
x
y
O
x=-1
小结(1)二次函数解析式的三种表示形式
(1)一般式
(2)顶点式
(3)交点式
同课章节目录
