人教版九年级数学上册 24.1 圆的有关性质复习讲义(Word版 无答案)
文档属性
| 名称 | 人教版九年级数学上册 24.1 圆的有关性质复习讲义(Word版 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 538.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 21:54:49 | ||
图片预览



文档简介
第二十四章
圆
圆的有关性质
知识点一
1.圆的定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的封闭曲线叫做圆。固定的端点O叫做圆心,线段OA叫做半径,以点O为圆心的圆,记作☉O,读作“圆O”.
2.与圆有关的概念
(1)弦和直径(连结圆上任意两点的线段叫做弦,经过圆心的弦叫做直径)
弧和半圆(圆上任意两点间的部分叫做弧,圆的任意一条直径的两个端点分圆成两条
弧,每一条弧都叫做半圆),大于半圆的弧叫优弧(优弧用⌒和三个字母表示)、小于半圆的弧叫劣弧(用⌒和两个字母表示).
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
运用垂径定理解题时的模型如下:如图,设⊙O的半径为r,圆心到弦的距离是d,弦长是a,三者之间的关系是
常见的辅助线:(1)连半径,构造直角三角形;(2)作弦心距,构造直角三角形.
注:用于计算时,一般先连结过弦的一个端点的半径或者作弦心距,构造Rt△,再结合勾股定理求解.
典例精析
例1.如图,AB
为圆
O
的直径,弦
CD⊥AB,垂足为点
E,连结
OC,若
AB=10,CD=8,则
AE
的长度为(
)
A.2.5
B.3
C.2
D.1
或4
【变式1】如图,AB
为圆
O
的直径,弦
CD⊥AB,垂足为点
E,连结
OC。若AE长为2,CD长为8,半径为
.
【变式2】如图,⊙O的半径为10,M是AB的中点,且OM=6,则⊙O的弦AB等于(
)
A.8
B.10
C.12
D.16
【变式3】在⊙O中,P为圆内一点,过点P的最长弦的长为8cm,最短的弦的长为4cm,则OP的长为( )
A.2
cm
B.2
cm
C.2cm
D.1cm
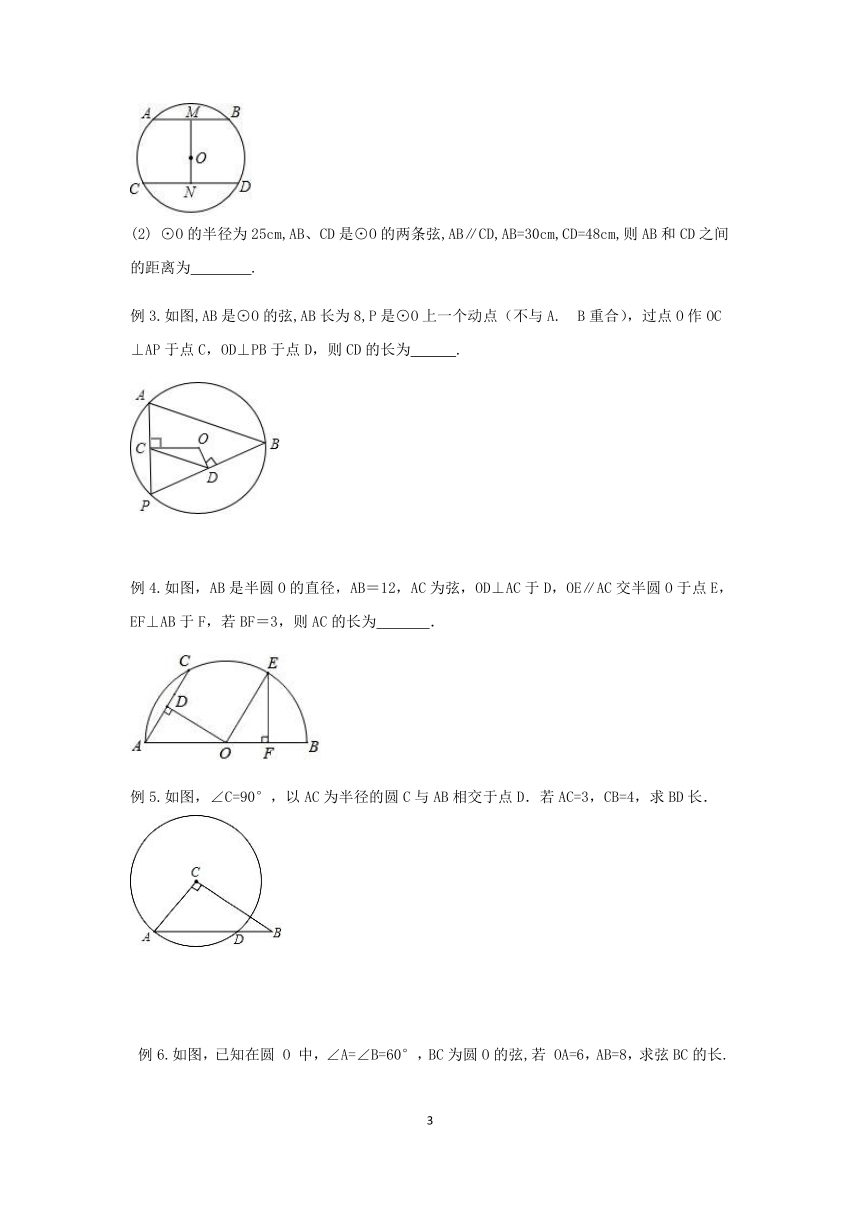
例2.(1)如图,⊙O的半径为5,弦AB∥CD,且AB=6,CD=8,过点O作OM⊥AB于点M,交CD于点N,则MN的长是_________.
⊙O的半径为25cm,AB、CD是⊙O的两条弦,AB∥CD,AB=30cm,CD=48cm,则AB和CD之间的距离为
.
例3.如图,AB是⊙O的弦,AB长为8,P是⊙O上一个动点(不与A.?B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为
.
例4.如图,AB是半圆O的直径,AB=12,AC为弦,OD⊥AC于D,OE∥AC交半圆O于点E,EF⊥AB于F,若BF=3,则AC的长为
.
例5.如图,∠C=90°,以AC为半径的圆C与AB相交于点D.若AC=3,CB=4,求BD长.
例6.如图,已知在圆
O
中,∠A=∠B=60°,BC为圆O的弦,若
OA=6,AB=8,求弦BC的长.
基础训练
1.下列命题中,正确的是(
)
A.平分一条直径的弦必垂直于这条直径
B.平分一条弧的直线垂直于这条弧所对的弦
C.弦的垂线必经过这条弦所在圆的圆心
D.在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心
2.点
P
到⊙O
的最近点的距离为
4cm,最远点的距离为
9cm,则⊙O
的半径是(
)
A.2.5cm
或
6.5cm
B.2.5cm
C.6.5cm
D.13cm
或
5cm
3.P
为⊙O
内一点,OP=3cm,⊙O
半径为
5cm,则经过
P
点的最短弦长为
;最长弦长为
.
4.已知AB是⊙O的弦,AB=8cm,OC⊥AB与C,OC=3cm,则⊙O的半径为
cm.
5.在直径为10cm的圆中,弦AB的长为8cm,则它的弦心距为
cm.
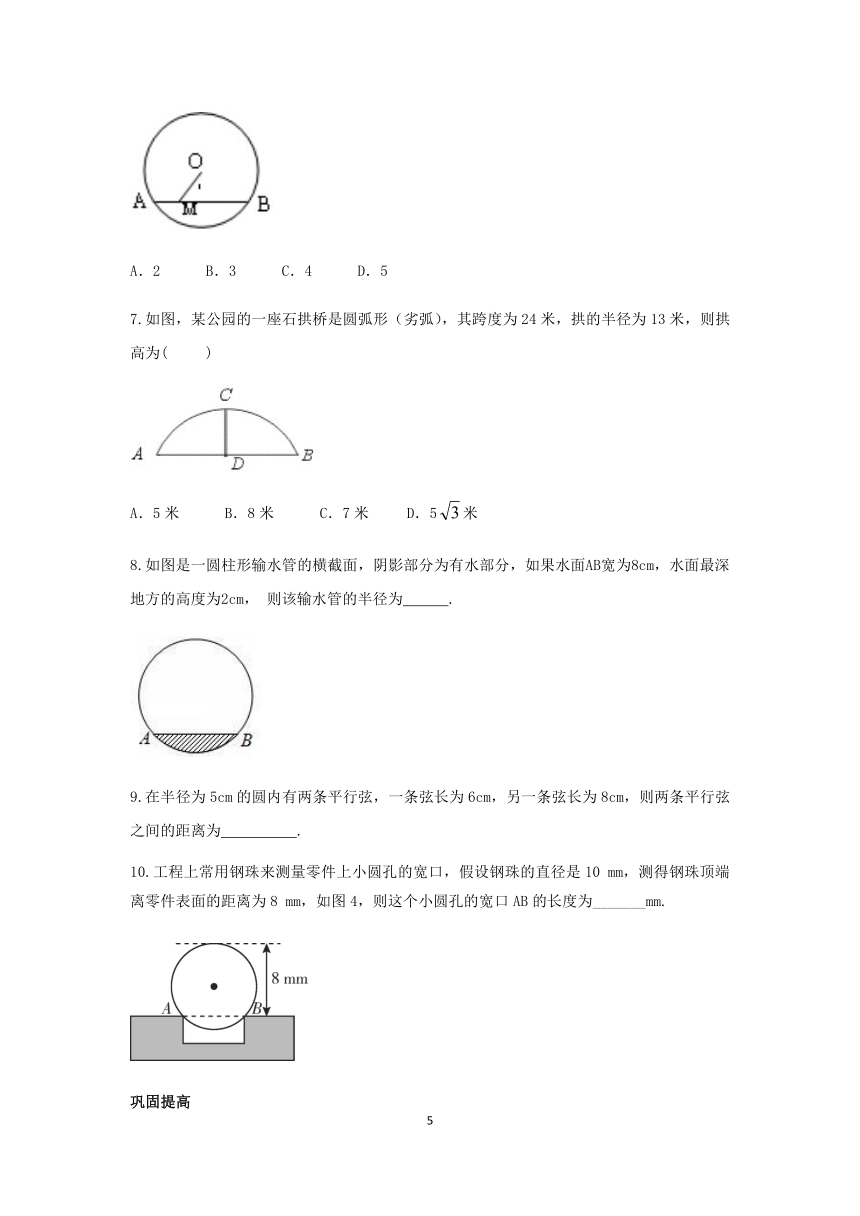
6.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的一个动点,则线段OM长的最小值为( )
A.2
B.3
C.4
D.5
7.如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为(
)
A.5米
B.8米
C.7米
D.5米
8.如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面
AB
宽为
8cm,水面最深地方的高度为
2cm,
则该输水管的半径为
.
9.在半径为5cm的圆内有两条平行弦,一条弦长为6cm,另一条弦长为8cm,则两条平行弦之间的距离为??
?
?.
10.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10
mm,测得钢珠顶端离零件表面的距离为8
mm,如图4,则这个小圆孔的宽口AB的长度为_______mm.
巩固提高
1.如图,在☉O中,弦AB⊥AC,OD⊥AB于点D,OE⊥AC于点E,若AB=8
cm,AC=6
cm,则☉O的半径OA的长为( )
A.7
cm B.6
cm C.5
cm D.4
cm
2.如图,⊙O的直径AB垂直于弦CD,垂足为E,若∠COD=120°,OE=3cm,则CD=
cm.
3.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EB.若AB=4,CD=1,则EB的长为( )
A.3
B.4
C.5
D.2.5
4.如图,的直径垂直弦于,且是半径的中点,,则直径的长是( )
A.
B.
C.
D.
5.如图,O的半径OA=6,以A为圆心,OA为半径的弧交O于B、C点,则BC=(
)
A.6
B.6
C.?3
D.3
6.已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,那么BC边上的高为(
)
A.2
B.8
C.2或8
D.2或3
7.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在弧MN上,且不与M,N重合,当P点在弧MN上移动时,矩形PAOB的形状、大小随之变化,则的值(
)
A.
变大
B.
变小
C.
不变
D.
不能确定
8.如图,AB为☉O的弦,P为AB上一点,且PA=8,PB=6,OP=4,则☉O的半径为 .?
9.下图是由两个长方形组成的工件平面图(单位:mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是 mm.?
10.如图,AB
是⊙O
的直径,弦
CD⊥AB
于点
E,∠CDB=30°,⊙O
的半径为cm,则弦
CD
的长为
.
11.如图,已知⊙O
的直径
AB
和弦
CD
交于
E,已知
AE=6cm,EB=2cm,∠CEA=30°.求弦
CD
的长.
12.如图,⊙O是△ABC的外接圆,圆心O在这个三角形的高AD上,AB=10,BC=12.
求⊙O的半径.
13.如图,已知
Rt△ABC
中,∠C=90°,以
C
为圆心,CA
为半径作圆
C,与
AB、BC
分别交于
D、E
两点.若
AC=4,
BC=8,求
AB
及
AD
的长度.
14.如图,在半径为5的四分之一圆中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=6时,求线段OD的长;
(2)连接AB,求DE的长.
尖子培优
1.如图,点C是⊙O上一点,⊙O的半径为,D,E分别是弦AC,BC上一动点,且OD=OE=,则AB的最大值为( )
A.2 B.2 C.2 D.4
2.在平面直角坐标系中,以原点O为圆心的圆过点A(0,3),直线y=kx-3k+4(k≠0)与☉O交于B,C两点,则弦BC的长的最小值为 .?
3.如图,在半径为1米,圆心角为60°的扇形中有一内接正方形CDEF,正方形CDEF面积为
.
4.如图,⊙O
过点
B、C,圆心
O
在等腰直角△ABC
的内部,∠BAC=90°,OA=1,BC=6,则圆
O
的半径为
.
5.如图,AB、CD
是半径为
5
的⊙O
的两条弦,AB=8,CD=6,MN
是直径,AB⊥
MN
于点
E,CD⊥M
N
于点
F,P
为
EF
上的任意一点,则
PA+PC
的最小值为多少.
知识点二
1.
圆心角:顶点在圆心的角叫做圆心角.将整个圆分为等份,每一份的弧对应的圆心角,我们也称这样的弧为的弧.圆心角的度数和它所对的弧的度数相等.
2.
圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角.
3.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧相等.
推论2:半圆(或直径)所对的圆周角是直角,的圆周角所对的弦是直径.
推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
4.
圆心角、弧、弦、弦心距之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量分别相等.
5.定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角.
典例精析
例1.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有(
)
①=;②=;③AC=BD;④∠BOD=∠AOC.
A.1个
B.2个
C.3个
D.4个
例2.如图,A,B,C,D是⊙O上的四点,且AD=BC,则AB与CD的大小关系为(
)
A.AB>CD
B.AB=CD
C.ABD.不能确定
例3.如图,A、B、C是⊙O上的三点,∠BAC=30°,则∠BOC的大小是(
)
A.60°
B.45°
C.30°
D.15°
例4.如图,A,B,C为⊙O上三点,∠OAB=50°,∠ACB=_______度.
例5圆的一条弦长等于它的半径,那么这条弦所对的圆周角的度数是________.
例6.已知,△ABC内接于O,BC是O的直径,点E在O上,OE∥AC,连结AE,若∠AEO=20°,则∠B的度数是_________.
例7.如图,半径为5的☉A经过点C和点O,点B是y轴右侧☉A的优弧上一点,∠OBC=30°,则点C的坐标为
.
?
例8.如图,半径为5的圆A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于(
)
A.
B.?
C.4
D.3
例9.如图,四边形ABCD内接于⊙O,F是上一点,且,连接CF并延长交AD的延长线于点E,连接AC。若∠ABC=105°,∠BAC=25°,则∠E的度数为
.
例10.如图,在O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=
.
例11.如图,∠AOB=90°,CD是弧AB的三等分点,连接AB分别交OC,OD于点E,F.?
求证:AE=BF=CD.
例12.如图,△ABC
内接于⊙O,∠BAC
与∠ABC
的角平分线
AE,BE
相交于点
E,延长
AE
交⊙O
于点
D,连接
BD,CD,
且∠BCA=60°.
(1)求∠BED的大小;
(2)求证:△BED为等边三角形;
(3)若∠ADC=30°,⊙O的半径为r,求等边三角形BED的边长.
基础训练
1.如图,在⊙O中,点C是的中点,∠A=50°,则∠BOC=(
)
A.40°
B.45°
C.50°
D.60°
2.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是(
)
A.51°
B.56°
C.68°
D.78°
3.
如图,直径AB垂直于弦CD,垂足为E,∠AOC=130°,
则弧AD的度数为_______,
∠CAD的度数为_____________,∠ACD的度数为
___________.
4.如图,是半圆的直径,为圆心,是半圆上一点,且,是延长线上一点,与半圆相交于点,如果,则
,
,
.
5.
如图,弧ACB与弧ADB的度数比是4:5,则
,
,
,
.
6.如图,△内接于圆O,,点,分别在弧AC和弧BC上,若,则
,
.
7.如图,已知:圆O是△的外接圆,,,则=_____度.
8.如图所示,四边形ABCD内接于圆O,∠BCD=120°,则∠BOD=____________度.
9.
若圆的一条弦把圆分成度数的比为1:3的两条弧,则劣弧所对的圆周角等于_____________.
10.在△ABC中,∠C=90°,AC=BC=4cm,D是AB边的中点,以点C为圆心,4cm为半径作圆。则A、B、C、D四点在圆内有_____________个.
11.如图,等边三角形ABC的三个顶点都在⊙O上,D是上任一点(不与A、C重合),则
∠ADC的度数是________.毛
12.如图四边形ABCD的四个顶点都在⊙O上,且AD∥BC,对角线AC与BC相交于点E,那么图中有______对相等的角.
13.已知,如图,∠BAD=100°,则∠BOC=_______度.
14.如图,AB是⊙O的直径,
,∠A=25°,则∠BOD的度数为________.
巩固提高
1.如图所示,△内接于⊙O,点是弧AC上任意一点(不与重合),的取值范围是
.
第1题
第2题
第4题
2.如图,AB是⊙O的直径,已知AB=2,C,D是⊙O上的两点,且+=,M是AB上一点,则MC+MD的最小值是 .?
3.已知在半径为2的O中,圆内接△ABC的边AB=2,则∠C的度数为
.
4.如图,A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB=_______度.
如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=
30°,
则点O
到CD
的距离OE=______,
OD=
.
第5题
第6题
第8题
6.如图所示,⊙O中,弦的延长线相交于点,如果,,那么
.
7.若O为的外心,且,则.
8.如图,⊙O的直径AB为4,点C在⊙O上,∠ACB的平分线交☉O于点D,连接AD、BD,则AD的长等于
.
综合题
1.如图,△ABC为等边三角形,点O在过点A且平行于BC的直线上运动,以△ABC的高为半径的⊙O分别交线段AB、AC于点E、F,则弧EF所对的圆周角的度数为 ( )
A.从0°到30°变化 B.从30°到60°变化
C.总等于30° D.总等于60°
2.如图,AB
是⊙O
直径,CD
是⊙O
弦,AB,CD
的延长线交于
E,AB=2DE,∠E=18°,∠C=
,
∠AOC=
_____________.
3.如图,AB是☉O的弦,AB=10,点C是☉O上的一个动点,且∠ACB=45°,若点M、N分别是AB、BC的中点,则MN长的最大值是 .?
4.如图,AB是☉O的一条弦,点C是☉O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与☉O交于G、H两点.若☉O的半径为7,则GE+FH的最大值为 .?
5.如图,AB是半圆O的直径,点C在半圆O上,AB=4
cm,∠CAB=60°,P是弧BC上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是 cm.?
如图,⊙O
的直径
AB=8,P
是圆上任一点(A、B
除外),∠APB
的平分线交⊙O
于
C,弦
EF
过
AC、BC
的中点
M、N,
则
EF
的长是
.
如图,⊙O
的半径是
2,直线
l
与⊙O
相交于
A、B
两点,M、N
是⊙O
上的两个动点,且在直线
l
的异侧,若∠
AMB=45°,则四边形
MANB
面积的最大值是
.
如图,已知⊙O
为△ABC
的外接圆,CE
是⊙O
的直径,CD⊥AB,D
为垂足.
求证:∠ACD=∠BCE.
9.已知四边形ABCD内接于O,∠D=90°,P为弧CD上一动点(不与点C,D重合).
(1)若∠BPC=30°,BC=3,求O的半径;
(2)若∠A=90°,弧AD=弧AB,求证:PB?PD=PC.
10.如图,点C为△ABD的外接圆上的一动点(点C不在弧BAD上,且不与点B,D重合),∠ACB=∠ABD=45°
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究,,三者之间满足的等量关系,并证明你的结论.
11.如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与A,C重合),延长BD至E.?
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30?,且△ABC底边BC边上高为1,求△ABC外接圆的周长.
12.如图,四边形ABCD是⊙O的内接四边形,点F
是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.?
?
⑴
求证:AB=AC.?
⑵
若BD=11,DE=2,求CD的长.
圆
圆的有关性质
知识点一
1.圆的定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的封闭曲线叫做圆。固定的端点O叫做圆心,线段OA叫做半径,以点O为圆心的圆,记作☉O,读作“圆O”.
2.与圆有关的概念
(1)弦和直径(连结圆上任意两点的线段叫做弦,经过圆心的弦叫做直径)
弧和半圆(圆上任意两点间的部分叫做弧,圆的任意一条直径的两个端点分圆成两条
弧,每一条弧都叫做半圆),大于半圆的弧叫优弧(优弧用⌒和三个字母表示)、小于半圆的弧叫劣弧(用⌒和两个字母表示).
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
运用垂径定理解题时的模型如下:如图,设⊙O的半径为r,圆心到弦的距离是d,弦长是a,三者之间的关系是
常见的辅助线:(1)连半径,构造直角三角形;(2)作弦心距,构造直角三角形.
注:用于计算时,一般先连结过弦的一个端点的半径或者作弦心距,构造Rt△,再结合勾股定理求解.
典例精析
例1.如图,AB
为圆
O
的直径,弦
CD⊥AB,垂足为点
E,连结
OC,若
AB=10,CD=8,则
AE
的长度为(
)
A.2.5
B.3
C.2
D.1
或4
【变式1】如图,AB
为圆
O
的直径,弦
CD⊥AB,垂足为点
E,连结
OC。若AE长为2,CD长为8,半径为
.
【变式2】如图,⊙O的半径为10,M是AB的中点,且OM=6,则⊙O的弦AB等于(
)
A.8
B.10
C.12
D.16
【变式3】在⊙O中,P为圆内一点,过点P的最长弦的长为8cm,最短的弦的长为4cm,则OP的长为( )
A.2
cm
B.2
cm
C.2cm
D.1cm
例2.(1)如图,⊙O的半径为5,弦AB∥CD,且AB=6,CD=8,过点O作OM⊥AB于点M,交CD于点N,则MN的长是_________.
⊙O的半径为25cm,AB、CD是⊙O的两条弦,AB∥CD,AB=30cm,CD=48cm,则AB和CD之间的距离为
.
例3.如图,AB是⊙O的弦,AB长为8,P是⊙O上一个动点(不与A.?B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为
.
例4.如图,AB是半圆O的直径,AB=12,AC为弦,OD⊥AC于D,OE∥AC交半圆O于点E,EF⊥AB于F,若BF=3,则AC的长为
.
例5.如图,∠C=90°,以AC为半径的圆C与AB相交于点D.若AC=3,CB=4,求BD长.
例6.如图,已知在圆
O
中,∠A=∠B=60°,BC为圆O的弦,若
OA=6,AB=8,求弦BC的长.
基础训练
1.下列命题中,正确的是(
)
A.平分一条直径的弦必垂直于这条直径
B.平分一条弧的直线垂直于这条弧所对的弦
C.弦的垂线必经过这条弦所在圆的圆心
D.在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心
2.点
P
到⊙O
的最近点的距离为
4cm,最远点的距离为
9cm,则⊙O
的半径是(
)
A.2.5cm
或
6.5cm
B.2.5cm
C.6.5cm
D.13cm
或
5cm
3.P
为⊙O
内一点,OP=3cm,⊙O
半径为
5cm,则经过
P
点的最短弦长为
;最长弦长为
.
4.已知AB是⊙O的弦,AB=8cm,OC⊥AB与C,OC=3cm,则⊙O的半径为
cm.
5.在直径为10cm的圆中,弦AB的长为8cm,则它的弦心距为
cm.
6.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的一个动点,则线段OM长的最小值为( )
A.2
B.3
C.4
D.5
7.如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为(
)
A.5米
B.8米
C.7米
D.5米
8.如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面
AB
宽为
8cm,水面最深地方的高度为
2cm,
则该输水管的半径为
.
9.在半径为5cm的圆内有两条平行弦,一条弦长为6cm,另一条弦长为8cm,则两条平行弦之间的距离为??
?
?.
10.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10
mm,测得钢珠顶端离零件表面的距离为8
mm,如图4,则这个小圆孔的宽口AB的长度为_______mm.
巩固提高
1.如图,在☉O中,弦AB⊥AC,OD⊥AB于点D,OE⊥AC于点E,若AB=8
cm,AC=6
cm,则☉O的半径OA的长为( )
A.7
cm B.6
cm C.5
cm D.4
cm
2.如图,⊙O的直径AB垂直于弦CD,垂足为E,若∠COD=120°,OE=3cm,则CD=
cm.
3.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EB.若AB=4,CD=1,则EB的长为( )
A.3
B.4
C.5
D.2.5
4.如图,的直径垂直弦于,且是半径的中点,,则直径的长是( )
A.
B.
C.
D.
5.如图,O的半径OA=6,以A为圆心,OA为半径的弧交O于B、C点,则BC=(
)
A.6
B.6
C.?3
D.3
6.已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,那么BC边上的高为(
)
A.2
B.8
C.2或8
D.2或3
7.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在弧MN上,且不与M,N重合,当P点在弧MN上移动时,矩形PAOB的形状、大小随之变化,则的值(
)
A.
变大
B.
变小
C.
不变
D.
不能确定
8.如图,AB为☉O的弦,P为AB上一点,且PA=8,PB=6,OP=4,则☉O的半径为 .?
9.下图是由两个长方形组成的工件平面图(单位:mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是 mm.?
10.如图,AB
是⊙O
的直径,弦
CD⊥AB
于点
E,∠CDB=30°,⊙O
的半径为cm,则弦
CD
的长为
.
11.如图,已知⊙O
的直径
AB
和弦
CD
交于
E,已知
AE=6cm,EB=2cm,∠CEA=30°.求弦
CD
的长.
12.如图,⊙O是△ABC的外接圆,圆心O在这个三角形的高AD上,AB=10,BC=12.
求⊙O的半径.
13.如图,已知
Rt△ABC
中,∠C=90°,以
C
为圆心,CA
为半径作圆
C,与
AB、BC
分别交于
D、E
两点.若
AC=4,
BC=8,求
AB
及
AD
的长度.
14.如图,在半径为5的四分之一圆中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=6时,求线段OD的长;
(2)连接AB,求DE的长.
尖子培优
1.如图,点C是⊙O上一点,⊙O的半径为,D,E分别是弦AC,BC上一动点,且OD=OE=,则AB的最大值为( )
A.2 B.2 C.2 D.4
2.在平面直角坐标系中,以原点O为圆心的圆过点A(0,3),直线y=kx-3k+4(k≠0)与☉O交于B,C两点,则弦BC的长的最小值为 .?
3.如图,在半径为1米,圆心角为60°的扇形中有一内接正方形CDEF,正方形CDEF面积为
.
4.如图,⊙O
过点
B、C,圆心
O
在等腰直角△ABC
的内部,∠BAC=90°,OA=1,BC=6,则圆
O
的半径为
.
5.如图,AB、CD
是半径为
5
的⊙O
的两条弦,AB=8,CD=6,MN
是直径,AB⊥
MN
于点
E,CD⊥M
N
于点
F,P
为
EF
上的任意一点,则
PA+PC
的最小值为多少.
知识点二
1.
圆心角:顶点在圆心的角叫做圆心角.将整个圆分为等份,每一份的弧对应的圆心角,我们也称这样的弧为的弧.圆心角的度数和它所对的弧的度数相等.
2.
圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角.
3.
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧相等.
推论2:半圆(或直径)所对的圆周角是直角,的圆周角所对的弦是直径.
推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
4.
圆心角、弧、弦、弦心距之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量分别相等.
5.定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角.
典例精析
例1.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有(
)
①=;②=;③AC=BD;④∠BOD=∠AOC.
A.1个
B.2个
C.3个
D.4个
例2.如图,A,B,C,D是⊙O上的四点,且AD=BC,则AB与CD的大小关系为(
)
A.AB>CD
B.AB=CD
C.AB
例3.如图,A、B、C是⊙O上的三点,∠BAC=30°,则∠BOC的大小是(
)
A.60°
B.45°
C.30°
D.15°
例4.如图,A,B,C为⊙O上三点,∠OAB=50°,∠ACB=_______度.
例5圆的一条弦长等于它的半径,那么这条弦所对的圆周角的度数是________.
例6.已知,△ABC内接于O,BC是O的直径,点E在O上,OE∥AC,连结AE,若∠AEO=20°,则∠B的度数是_________.
例7.如图,半径为5的☉A经过点C和点O,点B是y轴右侧☉A的优弧上一点,∠OBC=30°,则点C的坐标为
.
?
例8.如图,半径为5的圆A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于(
)
A.
B.?
C.4
D.3
例9.如图,四边形ABCD内接于⊙O,F是上一点,且,连接CF并延长交AD的延长线于点E,连接AC。若∠ABC=105°,∠BAC=25°,则∠E的度数为
.
例10.如图,在O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=
.
例11.如图,∠AOB=90°,CD是弧AB的三等分点,连接AB分别交OC,OD于点E,F.?
求证:AE=BF=CD.
例12.如图,△ABC
内接于⊙O,∠BAC
与∠ABC
的角平分线
AE,BE
相交于点
E,延长
AE
交⊙O
于点
D,连接
BD,CD,
且∠BCA=60°.
(1)求∠BED的大小;
(2)求证:△BED为等边三角形;
(3)若∠ADC=30°,⊙O的半径为r,求等边三角形BED的边长.
基础训练
1.如图,在⊙O中,点C是的中点,∠A=50°,则∠BOC=(
)
A.40°
B.45°
C.50°
D.60°
2.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是(
)
A.51°
B.56°
C.68°
D.78°
3.
如图,直径AB垂直于弦CD,垂足为E,∠AOC=130°,
则弧AD的度数为_______,
∠CAD的度数为_____________,∠ACD的度数为
___________.
4.如图,是半圆的直径,为圆心,是半圆上一点,且,是延长线上一点,与半圆相交于点,如果,则
,
,
.
5.
如图,弧ACB与弧ADB的度数比是4:5,则
,
,
,
.
6.如图,△内接于圆O,,点,分别在弧AC和弧BC上,若,则
,
.
7.如图,已知:圆O是△的外接圆,,,则=_____度.
8.如图所示,四边形ABCD内接于圆O,∠BCD=120°,则∠BOD=____________度.
9.
若圆的一条弦把圆分成度数的比为1:3的两条弧,则劣弧所对的圆周角等于_____________.
10.在△ABC中,∠C=90°,AC=BC=4cm,D是AB边的中点,以点C为圆心,4cm为半径作圆。则A、B、C、D四点在圆内有_____________个.
11.如图,等边三角形ABC的三个顶点都在⊙O上,D是上任一点(不与A、C重合),则
∠ADC的度数是________.毛
12.如图四边形ABCD的四个顶点都在⊙O上,且AD∥BC,对角线AC与BC相交于点E,那么图中有______对相等的角.
13.已知,如图,∠BAD=100°,则∠BOC=_______度.
14.如图,AB是⊙O的直径,
,∠A=25°,则∠BOD的度数为________.
巩固提高
1.如图所示,△内接于⊙O,点是弧AC上任意一点(不与重合),的取值范围是
.
第1题
第2题
第4题
2.如图,AB是⊙O的直径,已知AB=2,C,D是⊙O上的两点,且+=,M是AB上一点,则MC+MD的最小值是 .?
3.已知在半径为2的O中,圆内接△ABC的边AB=2,则∠C的度数为
.
4.如图,A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB=_______度.
如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=
30°,
则点O
到CD
的距离OE=______,
OD=
.
第5题
第6题
第8题
6.如图所示,⊙O中,弦的延长线相交于点,如果,,那么
.
7.若O为的外心,且,则.
8.如图,⊙O的直径AB为4,点C在⊙O上,∠ACB的平分线交☉O于点D,连接AD、BD,则AD的长等于
.
综合题
1.如图,△ABC为等边三角形,点O在过点A且平行于BC的直线上运动,以△ABC的高为半径的⊙O分别交线段AB、AC于点E、F,则弧EF所对的圆周角的度数为 ( )
A.从0°到30°变化 B.从30°到60°变化
C.总等于30° D.总等于60°
2.如图,AB
是⊙O
直径,CD
是⊙O
弦,AB,CD
的延长线交于
E,AB=2DE,∠E=18°,∠C=
,
∠AOC=
_____________.
3.如图,AB是☉O的弦,AB=10,点C是☉O上的一个动点,且∠ACB=45°,若点M、N分别是AB、BC的中点,则MN长的最大值是 .?
4.如图,AB是☉O的一条弦,点C是☉O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与☉O交于G、H两点.若☉O的半径为7,则GE+FH的最大值为 .?
5.如图,AB是半圆O的直径,点C在半圆O上,AB=4
cm,∠CAB=60°,P是弧BC上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是 cm.?
如图,⊙O
的直径
AB=8,P
是圆上任一点(A、B
除外),∠APB
的平分线交⊙O
于
C,弦
EF
过
AC、BC
的中点
M、N,
则
EF
的长是
.
如图,⊙O
的半径是
2,直线
l
与⊙O
相交于
A、B
两点,M、N
是⊙O
上的两个动点,且在直线
l
的异侧,若∠
AMB=45°,则四边形
MANB
面积的最大值是
.
如图,已知⊙O
为△ABC
的外接圆,CE
是⊙O
的直径,CD⊥AB,D
为垂足.
求证:∠ACD=∠BCE.
9.已知四边形ABCD内接于O,∠D=90°,P为弧CD上一动点(不与点C,D重合).
(1)若∠BPC=30°,BC=3,求O的半径;
(2)若∠A=90°,弧AD=弧AB,求证:PB?PD=PC.
10.如图,点C为△ABD的外接圆上的一动点(点C不在弧BAD上,且不与点B,D重合),∠ACB=∠ABD=45°
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究,,三者之间满足的等量关系,并证明你的结论.
11.如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与A,C重合),延长BD至E.?
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30?,且△ABC底边BC边上高为1,求△ABC外接圆的周长.
12.如图,四边形ABCD是⊙O的内接四边形,点F
是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.?
?
⑴
求证:AB=AC.?
⑵
若BD=11,DE=2,求CD的长.
同课章节目录
