人教版数学八年级上册数学 11.2.2三角形的外角 课件(共19张)
文档属性
| 名称 | 人教版数学八年级上册数学 11.2.2三角形的外角 课件(共19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-13 10:53:15 | ||
图片预览



文档简介
(共19张PPT)
§11.2.2
三角形的外角(1)
学习目标
会识别三角形的外角;
能探索出三角形的外角与内角的关系;
3.
会证明探索出来的结论;
4.运用三角形外角的性质进行有关计算。
一、温故知新
1、三角形三个内角的和等于多少度?
三角形的内角和等于180度
2、见导学案
A
B
C
D
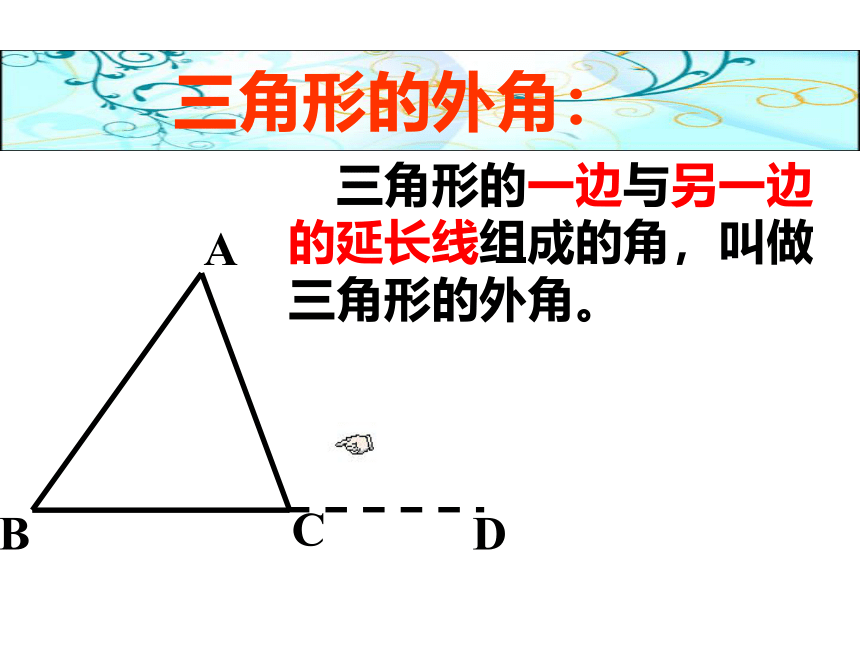
三角形的外角:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角。
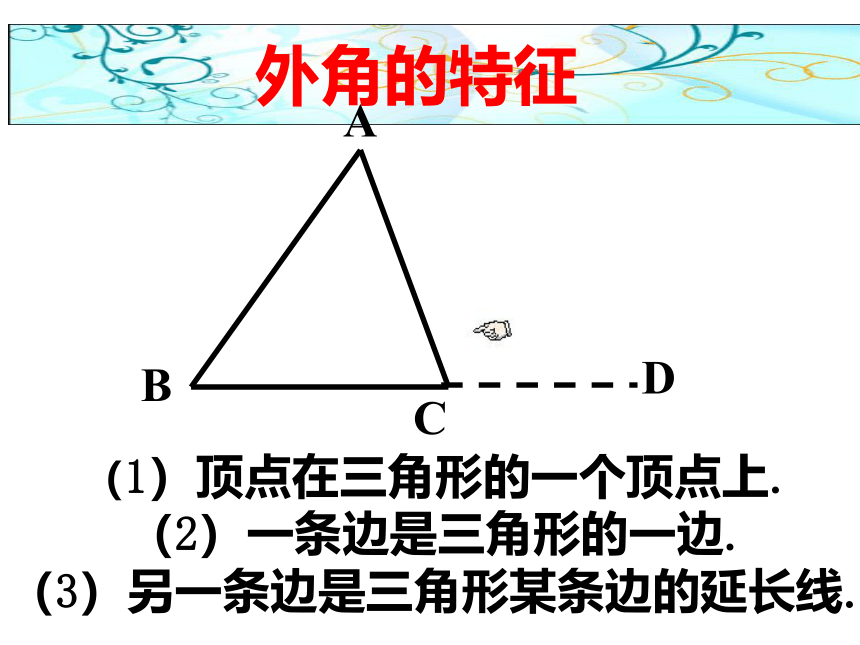
外角的特征
D
A
B
C
(1)顶点在三角形的一个顶点上.
(2)一条边是三角形的一边.
(3)另一条边是三角形某条边的延长线.
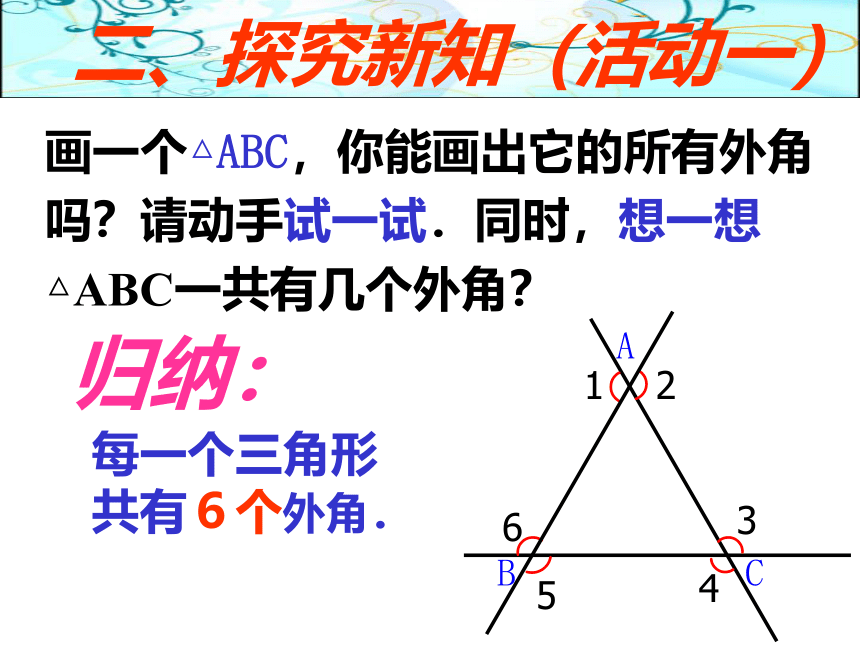
画一个△ABC,你能画出它的所有外角吗?请动手试一试.同时,想一想△ABC一共有几个外角?
归纳:
每一个三角形共有6个外角.
二、探究新知(活动一)
A
B
C
1
2
3
4
5
6
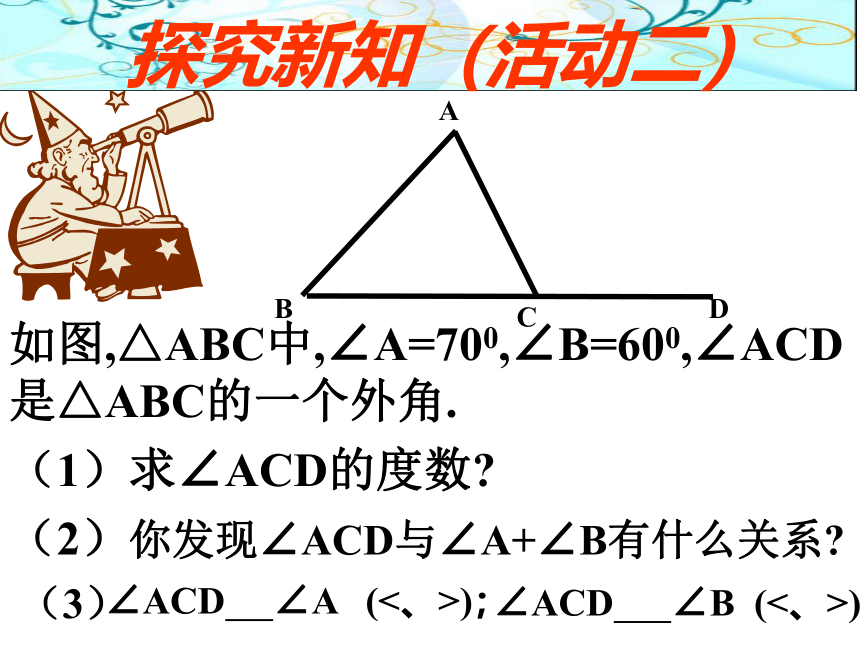
如图,△ABC中,∠A=700,∠B=600,∠ACD是△ABC的一个外角.
(1)求∠ACD的度数?
(2)你发现∠ACD与∠A+∠B有什么关系?
(3)
A
B
C
D
探究新知(活动二)
∠ACD
∠A
(<、>);
∠ACD
∠B
(<、>)
D
A
B
C
不相邻内角
1
2
3
4
.
1、外角与相邻内角有什么特殊关系?
外角
∠4+∠3=180°
相邻内角
探索,猜想:
2、外角与不相邻内角有什么关系?
(1)
∠4=∠1+∠2,
(2)∠4﹥∠1
,∠4﹥∠2。
A
B
D
C
1
2
E
已知:∠ACD是△ABC的一个外角
求证:
∠A+
∠B=
∠ACD
∠ACD
﹥A
、∠ACD
﹥B
证明:过C作CE∥AB
∴∠1=
∠A
(两直线平行,内错角相等)
∠2=∠B(两直线平行,同位角角相等)
∴
∠1
+∠2=∠A+∠B(等式性质)
即∠A+
∠B=
∠ACD
(等量代换)
∴
∠ACD
﹥A
、∠ACD
﹥B
(不等式性质)
三、合作交流(证明命题)
外角的性质
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任何一个内角.
四、应用新知(活动三)
∠BAE
∠CBF
∠ACD
是△ABC的三个外角,他们的和是多少?
三角形的外角和等于360°
F
C
B
D
E
A
1
2
3
基本思想:转化
让
我
们
展
开
想
象
的
翅
膀
解:∵
∠BAE
∠CBF
∠ACD
是△ABC的三个外角(已知)
∴
∠BAE
=∠3
+
∠2
∠CBF
=∠1+∠3
∠ACD
=∠1+∠2
∴
∠BAE
+∠CBF
+
∠ACD
=
2(∠3
+
∠2
+∠1)
∵∠3
+
∠2
+∠1=180°
∠BAE
+∠CBF
+
∠ACD=360°
F
C
B
D
E
A
1
2
3
谁最快:
1.求下列图中∠1的度数。
1
1
1
2、∠1,∠2,∠3各是哪个三角形的外角?
3、
∠1
,∠3和∠A哪个最大?为什么?
A
B
C
D
E
1
2
3
4、已知图中∠A、
∠B、
∠C分别为80°,
20°
,
30°
,求∠1的度数?
B
3
2
1
A
C
D
E
如图,计算∠BOC
拓展延伸
谈谈你有哪些收获!
1、三角形的一个外角与它相邻的内角互补
\
2、三角形的一个外角等于与它不相邻
的两个内角的和。
3、三角形的一个外角大于任何一个与它不相邻的内角。
4、三角形的外角和是360度
再见
§11.2.2
三角形的外角(1)
学习目标
会识别三角形的外角;
能探索出三角形的外角与内角的关系;
3.
会证明探索出来的结论;
4.运用三角形外角的性质进行有关计算。
一、温故知新
1、三角形三个内角的和等于多少度?
三角形的内角和等于180度
2、见导学案
A
B
C
D
三角形的外角:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角。
外角的特征
D
A
B
C
(1)顶点在三角形的一个顶点上.
(2)一条边是三角形的一边.
(3)另一条边是三角形某条边的延长线.
画一个△ABC,你能画出它的所有外角吗?请动手试一试.同时,想一想△ABC一共有几个外角?
归纳:
每一个三角形共有6个外角.
二、探究新知(活动一)
A
B
C
1
2
3
4
5
6
如图,△ABC中,∠A=700,∠B=600,∠ACD是△ABC的一个外角.
(1)求∠ACD的度数?
(2)你发现∠ACD与∠A+∠B有什么关系?
(3)
A
B
C
D
探究新知(活动二)
∠ACD
∠A
(<、>);
∠ACD
∠B
(<、>)
D
A
B
C
不相邻内角
1
2
3
4
.
1、外角与相邻内角有什么特殊关系?
外角
∠4+∠3=180°
相邻内角
探索,猜想:
2、外角与不相邻内角有什么关系?
(1)
∠4=∠1+∠2,
(2)∠4﹥∠1
,∠4﹥∠2。
A
B
D
C
1
2
E
已知:∠ACD是△ABC的一个外角
求证:
∠A+
∠B=
∠ACD
∠ACD
﹥A
、∠ACD
﹥B
证明:过C作CE∥AB
∴∠1=
∠A
(两直线平行,内错角相等)
∠2=∠B(两直线平行,同位角角相等)
∴
∠1
+∠2=∠A+∠B(等式性质)
即∠A+
∠B=
∠ACD
(等量代换)
∴
∠ACD
﹥A
、∠ACD
﹥B
(不等式性质)
三、合作交流(证明命题)
外角的性质
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任何一个内角.
四、应用新知(活动三)
∠BAE
∠CBF
∠ACD
是△ABC的三个外角,他们的和是多少?
三角形的外角和等于360°
F
C
B
D
E
A
1
2
3
基本思想:转化
让
我
们
展
开
想
象
的
翅
膀
解:∵
∠BAE
∠CBF
∠ACD
是△ABC的三个外角(已知)
∴
∠BAE
=∠3
+
∠2
∠CBF
=∠1+∠3
∠ACD
=∠1+∠2
∴
∠BAE
+∠CBF
+
∠ACD
=
2(∠3
+
∠2
+∠1)
∵∠3
+
∠2
+∠1=180°
∠BAE
+∠CBF
+
∠ACD=360°
F
C
B
D
E
A
1
2
3
谁最快:
1.求下列图中∠1的度数。
1
1
1
2、∠1,∠2,∠3各是哪个三角形的外角?
3、
∠1
,∠3和∠A哪个最大?为什么?
A
B
C
D
E
1
2
3
4、已知图中∠A、
∠B、
∠C分别为80°,
20°
,
30°
,求∠1的度数?
B
3
2
1
A
C
D
E
如图,计算∠BOC
拓展延伸
谈谈你有哪些收获!
1、三角形的一个外角与它相邻的内角互补
\
2、三角形的一个外角等于与它不相邻
的两个内角的和。
3、三角形的一个外角大于任何一个与它不相邻的内角。
4、三角形的外角和是360度
再见
