苏科版八年级数学上学期 2.2 轴对称的性质 同步练习(Word版 含答案)
文档属性
| 名称 | 苏科版八年级数学上学期 2.2 轴对称的性质 同步练习(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 199.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 00:00:00 | ||
图片预览


文档简介
2.2
轴对称的性质
一.选择题
1.两个图形关于某直线对称,对称点一定在( )
A.直线的两旁
B.直线的同旁
C.直线上
D.直线两旁或直线上
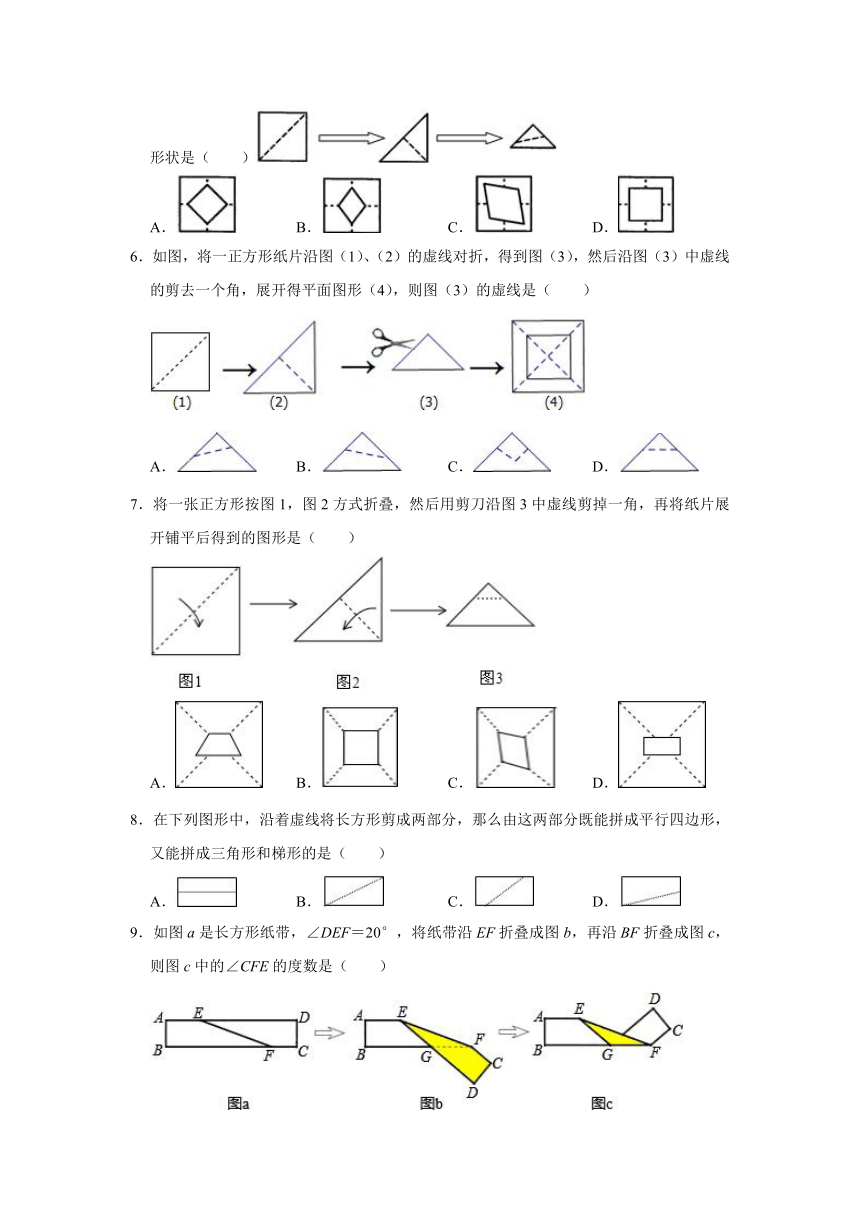
2.如图的2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有( )
A.2个
B.3个
C.4个
D.5个
3.如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
A.60°
B.50°
C.40°
D.70°
4.如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为( )
A.5cm
B.10cm
C.20cm
D.15cm
5.黄帅拿一张正方形的纸按如图所示沿虚线连续对折后剪去带直角的部分,然后打开后的形状是( )
A.
B.
C.
D.
6.如图,将一正方形纸片沿图(1)、(2)的虚线对折,得到图(3),然后沿图(3)中虚线的剪去一个角,展开得平面图形(4),则图(3)的虚线是( )
A.
B.
C.
D.
7.将一张正方形按图1,图2方式折叠,然后用剪刀沿图3中虚线剪掉一角,再将纸片展开铺平后得到的图形是( )
A.
B.
C.
D.
8.在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形,又能拼成三角形和梯形的是( )
A.
B.
C.
D.
9.如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.110°
B.120°
C.140°
D.150°
10.如图,在△ABC中,AC=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是( )
A.90°
B.120°
C.135°
D.150°
二.填空题
11.如图所示,已知O是∠APB内的一点,点M,N分别是O点关于PA,PB的对称点,MN与PA,PB分别相交于点E,F,已知MN=5cm,则△OEF的周长
cm.
12.已知∠AOB=45°,点P在∠AOB的内部,P1与P关于OB对称,P2与P关于OA对称,则P1,O,P2三点构成的三角形是
.
13.△ABC和△DEF关于直线l对称,若△ABC的周长为12cm,△DEF的面积为8cm2,则△DEF的周长为
,△ABC的面积为
.
14.如图是一个经过改造的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是
号袋.
15.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于
°.
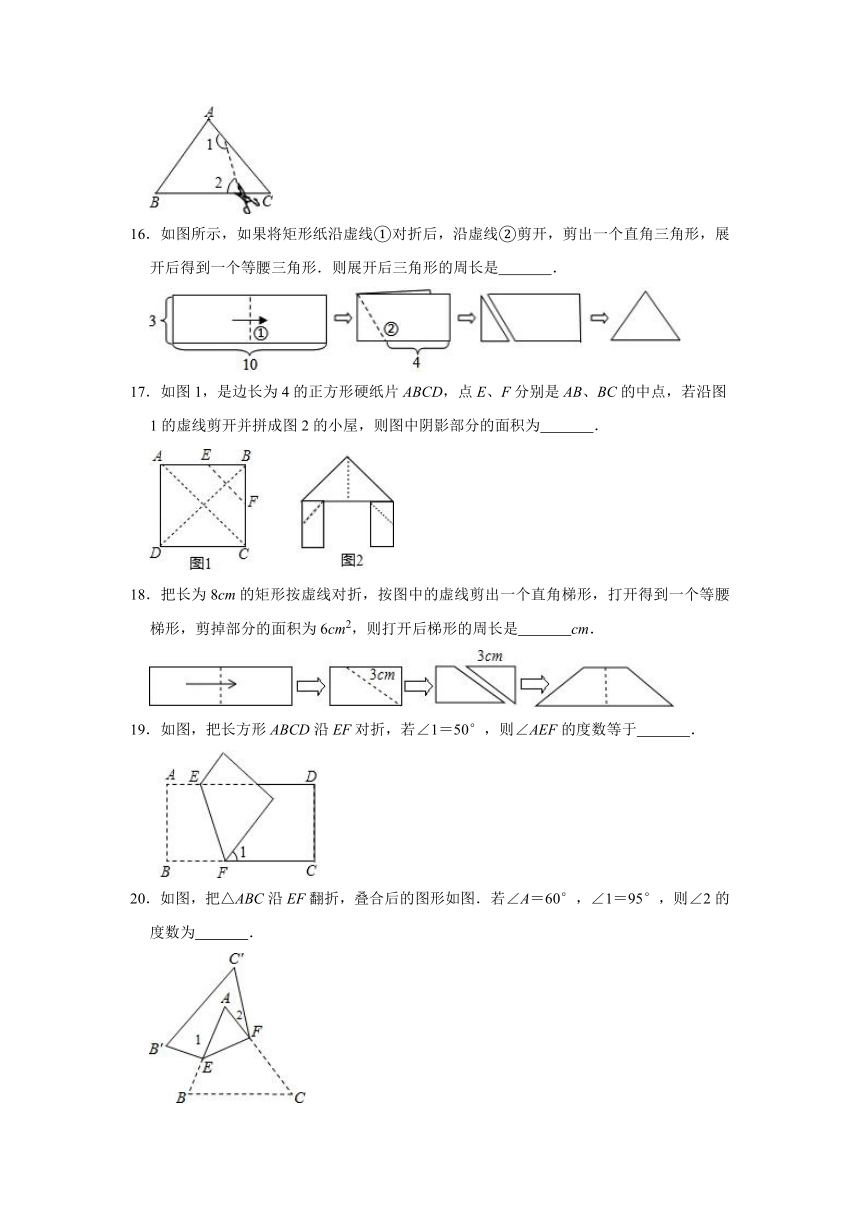
16.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是
.
17.如图1,是边长为4的正方形硬纸片ABCD,点E、F分别是AB、BC的中点,若沿图1的虚线剪开并拼成图2的小屋,则图中阴影部分的面积为
.
18.把长为8cm的矩形按虚线对折,按图中的虚线剪出一个直角梯形,打开得到一个等腰梯形,剪掉部分的面积为6cm2,则打开后梯形的周长是
cm.
19.如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于
.
20.如图,把△ABC沿EF翻折,叠合后的图形如图.若∠A=60°,∠1=95°,则∠2的度数为
.
三.解答题
21.如图所示,已知Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点落在AB边上的点D、要使点D恰为AB的中点,问在图中还要添加什么条件?(直接填写答案)
(1)写出两条边满足的条件:
;
(2)写出两个角满足的条件:
;
(3)写出一个除边、角以外的其他满足条件:
.
22.如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
23.图①是一张画有小方格的等腰直角三角形纸片,将图①按箭头方向折叠成图②,再将图②按箭头方向折叠成图③.
(1)请把上述两次折叠的折痕用实线画在图④中;
(2)在折叠后的图形③中,沿直线l剪掉标有A的部分,把剩余部分展开,将所得到的图形在图⑤中用阴影表示出来.
参考答案
一.选择题
1.
D.
2.
B.
3.
A.
4.
B.
5.
C.
6.
D.
7.
B.
8.
D.
9.
B.
10.
B.
二.填空题
11.
5.
12.等腰直角三角形.
13.
12cm,8cm2.
14.2.
15.
230°.
16.
2+2.
17.
4.
18.
10+2.
19.
115°.
20.
25°.
三.解答题
21.解:(1)①AB=BC
证明:由轴对称的性质可得:BC=BD,又因为BC=AB=BD
∴可得D在AB的中点位置.
(2)①∠ABC=2∠A.
∵∠C=90°,
∴∠ABC+∠A=90°.
∵∠ABC=2∠A,
∴∠A=30°.
由轴对称的性质得:BC=BD,CE=DE,∠CBE=∠DBE=∠A=30°.
∴△ADE≌△BCE,AD=BC=BD.
即点D在AB的中点;
(3)△BEC≌△AED
证明:∵△BEC≌△AED
∴可得:AD=DB
故证得点D在AB的中点.
22.解:(1)如图所示:△ABC的面积:×3×5=7.5;
(2)如图所示:
(3)A1(1,5),B1(1,0),C1(4,3).
23.解:(1)动手操作后只把折痕画出;
(4分)
(2)注意应折叠后,剪去该剪去的部分,再展开画出剩下部分.
(9分)
轴对称的性质
一.选择题
1.两个图形关于某直线对称,对称点一定在( )
A.直线的两旁
B.直线的同旁
C.直线上
D.直线两旁或直线上
2.如图的2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有( )
A.2个
B.3个
C.4个
D.5个
3.如图,如果直线是多边形的对称轴,其中∠A=130°,∠B=110°,那么∠BCD的度数等于( )
A.60°
B.50°
C.40°
D.70°
4.如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为( )
A.5cm
B.10cm
C.20cm
D.15cm
5.黄帅拿一张正方形的纸按如图所示沿虚线连续对折后剪去带直角的部分,然后打开后的形状是( )
A.
B.
C.
D.
6.如图,将一正方形纸片沿图(1)、(2)的虚线对折,得到图(3),然后沿图(3)中虚线的剪去一个角,展开得平面图形(4),则图(3)的虚线是( )
A.
B.
C.
D.
7.将一张正方形按图1,图2方式折叠,然后用剪刀沿图3中虚线剪掉一角,再将纸片展开铺平后得到的图形是( )
A.
B.
C.
D.
8.在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形,又能拼成三角形和梯形的是( )
A.
B.
C.
D.
9.如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.110°
B.120°
C.140°
D.150°
10.如图,在△ABC中,AC=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是( )
A.90°
B.120°
C.135°
D.150°
二.填空题
11.如图所示,已知O是∠APB内的一点,点M,N分别是O点关于PA,PB的对称点,MN与PA,PB分别相交于点E,F,已知MN=5cm,则△OEF的周长
cm.
12.已知∠AOB=45°,点P在∠AOB的内部,P1与P关于OB对称,P2与P关于OA对称,则P1,O,P2三点构成的三角形是
.
13.△ABC和△DEF关于直线l对称,若△ABC的周长为12cm,△DEF的面积为8cm2,则△DEF的周长为
,△ABC的面积为
.
14.如图是一个经过改造的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是
号袋.
15.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于
°.
16.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是
.
17.如图1,是边长为4的正方形硬纸片ABCD,点E、F分别是AB、BC的中点,若沿图1的虚线剪开并拼成图2的小屋,则图中阴影部分的面积为
.
18.把长为8cm的矩形按虚线对折,按图中的虚线剪出一个直角梯形,打开得到一个等腰梯形,剪掉部分的面积为6cm2,则打开后梯形的周长是
cm.
19.如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于
.
20.如图,把△ABC沿EF翻折,叠合后的图形如图.若∠A=60°,∠1=95°,则∠2的度数为
.
三.解答题
21.如图所示,已知Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点落在AB边上的点D、要使点D恰为AB的中点,问在图中还要添加什么条件?(直接填写答案)
(1)写出两条边满足的条件:
;
(2)写出两个角满足的条件:
;
(3)写出一个除边、角以外的其他满足条件:
.
22.如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
23.图①是一张画有小方格的等腰直角三角形纸片,将图①按箭头方向折叠成图②,再将图②按箭头方向折叠成图③.
(1)请把上述两次折叠的折痕用实线画在图④中;
(2)在折叠后的图形③中,沿直线l剪掉标有A的部分,把剩余部分展开,将所得到的图形在图⑤中用阴影表示出来.
参考答案
一.选择题
1.
D.
2.
B.
3.
A.
4.
B.
5.
C.
6.
D.
7.
B.
8.
D.
9.
B.
10.
B.
二.填空题
11.
5.
12.等腰直角三角形.
13.
12cm,8cm2.
14.2.
15.
230°.
16.
2+2.
17.
4.
18.
10+2.
19.
115°.
20.
25°.
三.解答题
21.解:(1)①AB=BC
证明:由轴对称的性质可得:BC=BD,又因为BC=AB=BD
∴可得D在AB的中点位置.
(2)①∠ABC=2∠A.
∵∠C=90°,
∴∠ABC+∠A=90°.
∵∠ABC=2∠A,
∴∠A=30°.
由轴对称的性质得:BC=BD,CE=DE,∠CBE=∠DBE=∠A=30°.
∴△ADE≌△BCE,AD=BC=BD.
即点D在AB的中点;
(3)△BEC≌△AED
证明:∵△BEC≌△AED
∴可得:AD=DB
故证得点D在AB的中点.
22.解:(1)如图所示:△ABC的面积:×3×5=7.5;
(2)如图所示:
(3)A1(1,5),B1(1,0),C1(4,3).
23.解:(1)动手操作后只把折痕画出;
(4分)
(2)注意应折叠后,剪去该剪去的部分,再展开画出剩下部分.
(9分)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
