北师大版九年级数学上册 第3章 概率的进一步认识 单元练习卷(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学上册 第3章 概率的进一步认识 单元练习卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 157.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 21:00:01 | ||
图片预览



文档简介
第3章
概率的进一步认识
一.选择题
1.在一个不透明的盒子里装有200个红、黄两种颜色的小球,这些球除颜色外其他完全相同,每次摸球前先将盒子里的球摇匀,任意摸出一个球,记下颜色后再放回盒子,通过大量重复试验后发现,摸到黄球的频率稳定在45%,那么估计盒子中黄球的个数为( )
A.80
B.90
C.100
D.110
2.某射击运动员在同一条件下的射击成绩记录如下:
射击次数
20
80
100
200
400
1000
“射中九环以上”的次数
18
68
82
168
327
823
“射中九环以上”的频率(结果保留两位小数)
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.90
B.0.82
C.0.85
D.0.84
3.从马鸣、杨豪、陆畅、江宽四人中抽调两人参加“寸草心”志愿服务队,恰好抽到马鸣和杨豪的概率是( )
A.
B.
C.
D.
4.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )
A.5
B.10
C.12
D.15
5.小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )
A.掷一枚质地均匀的硬币,正面朝上的概率
B.任意买一张电影票,座位号是2的倍数的概率
C.从一个装有4个黑球和2个白球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到白球的概率
D.从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率
6.在两个袋内,分别装着写有1、2、3、4四个数字的4张卡片,今从每个袋中各任取一张卡片,则所取两卡片上数字之积为偶数的概率是( )
A.
B.
C.
D.
7.如图.随机闭合开关K1、K2、K3中的两个,则能让两盏灯泡L1、L2同时发光的概率为( )
A.
B.
C.
D.
8.在一个不透明的布袋中装有52个白球和若干个黑球,除颜色外其他都相同,小强每次摸出一个球记录下颜色后并放回,通过多次试验后发现,摸到黑球的频率稳定在0.2左右,则布袋中黑球的个数可能有( )
A.11
B.13
C.24
D.30
9.在两个不透明的口袋中分别装有两把不同的钥匙和三把锁,其中两把钥匙分别能打开两把锁,且不能打开第三把锁,随机取出一把钥匙和一把锁,能打开的概率是( )
A.
B.
C.
D.
10.四张看上去无差别的卡片上分别印有正方形、正五边形、正六边形和圆,现将印有图形的一面朝下,混合均匀后从中随机抽取两张,则抽到的卡片上印有的图形都是中心对称图形的概率为( )
A.
B.
C.
D.
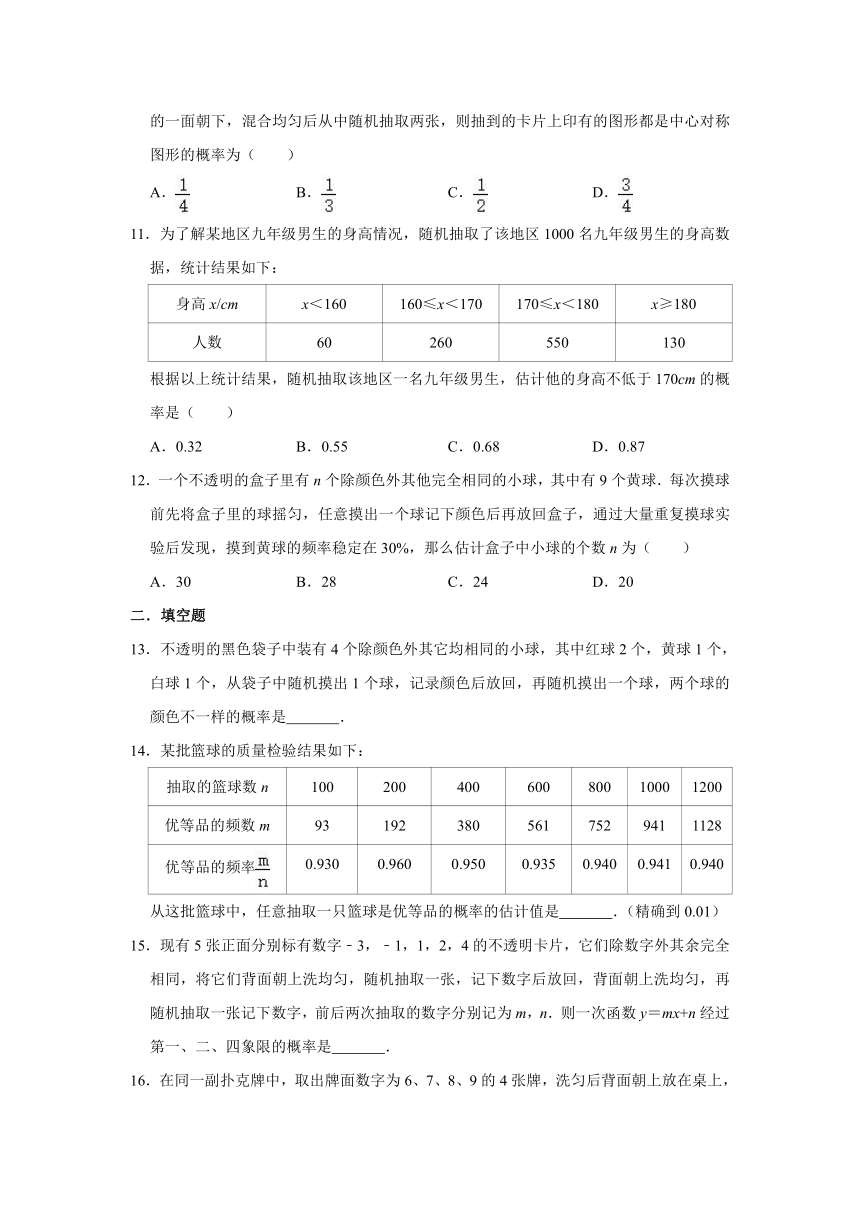
11.为了解某地区九年级男生的身高情况,随机抽取了该地区1000名九年级男生的身高数据,统计结果如下:
身高x/cm
x<160
160≤x<170
170≤x<180
x≥180
人数
60
260
550
130
根据以上统计结果,随机抽取该地区一名九年级男生,估计他的身高不低于170cm的概率是( )
A.0.32
B.0.55
C.0.68
D.0.87
12.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )
A.30
B.28
C.24
D.20
二.填空题
13.不透明的黑色袋子中装有4个除颜色外其它均相同的小球,其中红球2个,黄球1个,白球1个,从袋子中随机摸出1个球,记录颜色后放回,再随机摸出一个球,两个球的颜色不一样的概率是
.
14.某批篮球的质量检验结果如下:
抽取的篮球数n
100
200
400
600
800
1000
1200
优等品的频数m
93
192
380
561
752
941
1128
优等品的频率
0.930
0.960
0.950
0.935
0.940
0.941
0.940
从这批篮球中,任意抽取一只篮球是优等品的概率的估计值是
.(精确到0.01)
15.现有5张正面分别标有数字﹣3,﹣1,1,2,4的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为m,n.则一次函数y=mx+n经过第一、二、四象限的概率是
.
16.在同一副扑克牌中,取出牌面数字为6、7、8、9的4张牌,洗匀后背面朝上放在桌上,现从中随机摸出两张牌,则这两张牌上的数字之和为偶数的概率为
.
17.在一个不透明的盒子中装有红、白两种除颜色外完全相同的球,其中有a个白球和20个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在0.4左右,则a的值约为
.
18.经过人民中路十字路口红绿灯处的两辆汽车,可能直行,也可能向左转,如果这两种可能性大小相同,则至少有一辆向左转的概率是
.
三.解答题
19.一个不透明的口袋中装有2个红球和1个白球,小球除颜色外其余均相同.从口袋中随机摸出一个小球,记下颜色后放回,再随机摸出一个小球.请用画树状图(或列表)的方法,求两次摸出的小球颜色不同的概率.
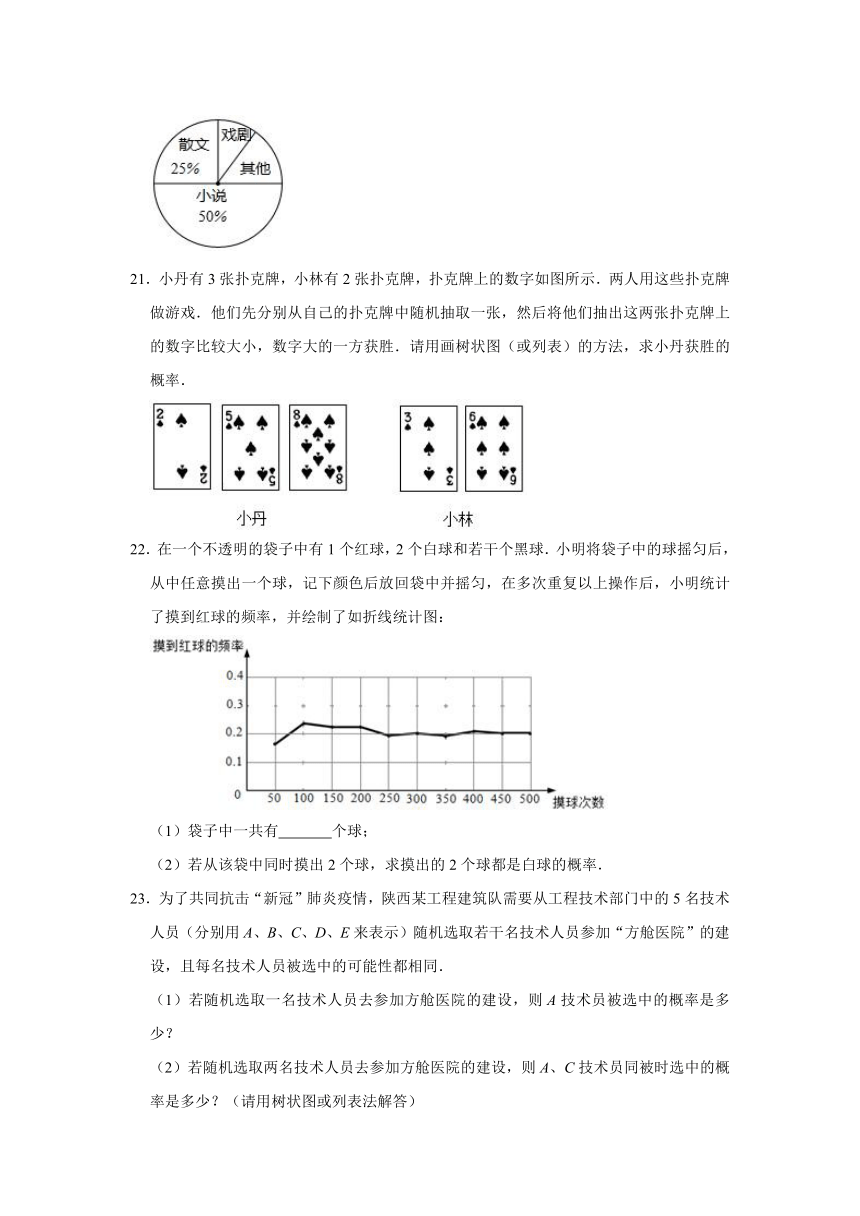
20.光明中学八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
(1)八年级一班一共有多少名学生?
(2)请补全频数分布表,在扇形统计图中,“戏剧”类对应的扇形圆形角是多少度?
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是甲和丙的概率.
类别
频数(人数)
频率
小说
0.5
戏剧
4
散文
10
0.25
其他
6
合计
m
1
21.小丹有3张扑克牌,小林有2张扑克牌,扑克牌上的数字如图所示.两人用这些扑克牌做游戏.他们先分别从自己的扑克牌中随机抽取一张,然后将他们抽出这两张扑克牌上的数字比较大小,数字大的一方获胜.请用画树状图(或列表)的方法,求小丹获胜的概率.
22.在一个不透明的袋子中有1个红球,2个白球和若干个黑球.小明将袋子中的球摇匀后,从中任意摸出一个球,记下颜色后放回袋中并摇匀,在多次重复以上操作后,小明统计了摸到红球的频率,并绘制了如折线统计图:
(1)袋子中一共有
个球;
(2)若从该袋中同时摸出2个球,求摸出的2个球都是白球的概率.
23.为了共同抗击“新冠”肺炎疫情,陕西某工程建筑队需要从工程技术部门中的5名技术人员(分别用A、B、C、D、E来表示)随机选取若干名技术人员参加“方舱医院”的建设,且每名技术人员被选中的可能性都相同.
(1)若随机选取一名技术人员去参加方舱医院的建设,则A技术员被选中的概率是多少?
(2)若随机选取两名技术人员去参加方舱医院的建设,则A、C技术员同被时选中的概率是多少?(请用树状图或列表法解答)
24.某校组织开展运动会,小明和扎西两名同学准备从100米短跑(记为项目A),800米中长跑(记为项目B),跳远(记为项目C),跳高(记为项目D),即从A,B,C,D四个项目中,分别选择一个项目参加比赛.请用画树状图或列表法求两名同学选到相同项目的概率.
25.某市林业局要移植一种树苗.对附近地区去年这种树苗移植成活的情况进行调查统计,并绘制了如图折线统计图:
(1)这种树苗成活概率的估计值为
.
(2)若移植这种树苗6000棵,估计可以成活
棵.
(3)若计划成活9000棵这种树苗,则需移植这种树苗大约多少棵?
26.某公司有甲、乙、丙三辆车去南京,它们出发的先后顺序随机.张先生和李先生乘坐该公司的车去南京出差,但有不同的需求.
请用所学概率知识解决下列问题:
(1)写出这三辆车按先后顺序出发的所有可能结果;
(2)两人中,谁乘坐到甲车的可能性大?请说明理由.
参考答案
一.选择题
1.
B.
2.
B.
3.
C.
4.
A.
5.
D.
6.
D.
7.
D.
8.
B.
9.
B.
10.
C.
11.
C.
12.
A.
二.填空题
13.
.
14.
0.94.
15.
.
16.
.
17.
30.
18.
.
三.解答题
19.
.
20.解:(1)10÷25%=40,
所以八年级一班一共有40名学生;
(2)阅读“小说”的人数为0.5×40=20(人);
阅读“戏剧”的人数的频率为=0.1;
阅读其它的人数的频率为=0.15;
在扇形统计图中,“戏剧”类对应的扇形圆形角的度数为360°×=36°;
故答案为20;0.1;0.15;
(3)画树状图为:
共有12种等可能的结果,其中选取的2人恰好是甲和丙的结果数为2,
所以选取的2人恰好是甲和丙的概率==.
21.解:画树状图得:
∵共有6种等可能的结果,小丹获胜的情况有3种,
∴P(小丹获胜)==.
22.解:(1)观察折线统计图可知:
摸到红球的频率稳定在0.2,
设袋子中有x个黑球,
所以=0.2,
解得x=2,
所以袋子中一共有5个球.
故答案为:5;
(2)解:将2个白球分别记作“白1”、“白2”,
2个黑球分别记作“黑1”、“黑2”.
从袋中同时摸出2个球,
可能出现的结果有10种,
即(红,白1),(红,白2),(红,黑1),(红,黑2),(白1,白2),(白1,黑1),(白1,黑2),(白2,黑1),(白2,黑2),(黑1,黑2),
并且它们出现的可能性相同.
其中2个球都是白球(记为事件A)的结果有1种,即(白1,白2),
所以P(A)=.
23.解:(1)A技术员被选中的概率为;
(2)画树状图为:
共有20种等可能的结果,其中A、C技术员同被时选中的结果数为2,
所以A、C技术员同被时选中的概率==.
24.解:画树状图得:
∵共有16种等可能的结果,两名同学选到相同项目的为4种情况,
∴P(两名同学选到相同项目)==.
25.解:(1)从折线统计图中的发展趋势,随着实验次数的增加,频率越稳定在0.9附近波动,根据频率估计概率,这种树苗成活概率约为0.9,
故答案为:0.9;
(2)6000×0.9=5400(棵),
故答案为:5400;
(3)9
000÷0.9=10000(棵),
答:需移植这种树苗大约10000棵.
26.解:(1)甲、乙、丙;甲、丙、乙;乙、甲、丙;乙、丙、甲;丙、甲、乙;丙、乙、甲;共6种;
(2)由(1)可知张先生坐到甲车有两种可能,乙、丙、甲,丙、乙、甲,
则张先生坐到甲车的概率是=;
由(1)可知李先生坐到甲车有两种可能,甲、乙、丙,甲、丙、乙,
则李先生坐到甲车的概率是=;
所以两人坐到甲车的可能性一样.
概率的进一步认识
一.选择题
1.在一个不透明的盒子里装有200个红、黄两种颜色的小球,这些球除颜色外其他完全相同,每次摸球前先将盒子里的球摇匀,任意摸出一个球,记下颜色后再放回盒子,通过大量重复试验后发现,摸到黄球的频率稳定在45%,那么估计盒子中黄球的个数为( )
A.80
B.90
C.100
D.110
2.某射击运动员在同一条件下的射击成绩记录如下:
射击次数
20
80
100
200
400
1000
“射中九环以上”的次数
18
68
82
168
327
823
“射中九环以上”的频率(结果保留两位小数)
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A.0.90
B.0.82
C.0.85
D.0.84
3.从马鸣、杨豪、陆畅、江宽四人中抽调两人参加“寸草心”志愿服务队,恰好抽到马鸣和杨豪的概率是( )
A.
B.
C.
D.
4.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )
A.5
B.10
C.12
D.15
5.小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )
A.掷一枚质地均匀的硬币,正面朝上的概率
B.任意买一张电影票,座位号是2的倍数的概率
C.从一个装有4个黑球和2个白球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到白球的概率
D.从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率
6.在两个袋内,分别装着写有1、2、3、4四个数字的4张卡片,今从每个袋中各任取一张卡片,则所取两卡片上数字之积为偶数的概率是( )
A.
B.
C.
D.
7.如图.随机闭合开关K1、K2、K3中的两个,则能让两盏灯泡L1、L2同时发光的概率为( )
A.
B.
C.
D.
8.在一个不透明的布袋中装有52个白球和若干个黑球,除颜色外其他都相同,小强每次摸出一个球记录下颜色后并放回,通过多次试验后发现,摸到黑球的频率稳定在0.2左右,则布袋中黑球的个数可能有( )
A.11
B.13
C.24
D.30
9.在两个不透明的口袋中分别装有两把不同的钥匙和三把锁,其中两把钥匙分别能打开两把锁,且不能打开第三把锁,随机取出一把钥匙和一把锁,能打开的概率是( )
A.
B.
C.
D.
10.四张看上去无差别的卡片上分别印有正方形、正五边形、正六边形和圆,现将印有图形的一面朝下,混合均匀后从中随机抽取两张,则抽到的卡片上印有的图形都是中心对称图形的概率为( )
A.
B.
C.
D.
11.为了解某地区九年级男生的身高情况,随机抽取了该地区1000名九年级男生的身高数据,统计结果如下:
身高x/cm
x<160
160≤x<170
170≤x<180
x≥180
人数
60
260
550
130
根据以上统计结果,随机抽取该地区一名九年级男生,估计他的身高不低于170cm的概率是( )
A.0.32
B.0.55
C.0.68
D.0.87
12.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )
A.30
B.28
C.24
D.20
二.填空题
13.不透明的黑色袋子中装有4个除颜色外其它均相同的小球,其中红球2个,黄球1个,白球1个,从袋子中随机摸出1个球,记录颜色后放回,再随机摸出一个球,两个球的颜色不一样的概率是
.
14.某批篮球的质量检验结果如下:
抽取的篮球数n
100
200
400
600
800
1000
1200
优等品的频数m
93
192
380
561
752
941
1128
优等品的频率
0.930
0.960
0.950
0.935
0.940
0.941
0.940
从这批篮球中,任意抽取一只篮球是优等品的概率的估计值是
.(精确到0.01)
15.现有5张正面分别标有数字﹣3,﹣1,1,2,4的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为m,n.则一次函数y=mx+n经过第一、二、四象限的概率是
.
16.在同一副扑克牌中,取出牌面数字为6、7、8、9的4张牌,洗匀后背面朝上放在桌上,现从中随机摸出两张牌,则这两张牌上的数字之和为偶数的概率为
.
17.在一个不透明的盒子中装有红、白两种除颜色外完全相同的球,其中有a个白球和20个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色后再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在0.4左右,则a的值约为
.
18.经过人民中路十字路口红绿灯处的两辆汽车,可能直行,也可能向左转,如果这两种可能性大小相同,则至少有一辆向左转的概率是
.
三.解答题
19.一个不透明的口袋中装有2个红球和1个白球,小球除颜色外其余均相同.从口袋中随机摸出一个小球,记下颜色后放回,再随机摸出一个小球.请用画树状图(或列表)的方法,求两次摸出的小球颜色不同的概率.
20.光明中学八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
(1)八年级一班一共有多少名学生?
(2)请补全频数分布表,在扇形统计图中,“戏剧”类对应的扇形圆形角是多少度?
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是甲和丙的概率.
类别
频数(人数)
频率
小说
0.5
戏剧
4
散文
10
0.25
其他
6
合计
m
1
21.小丹有3张扑克牌,小林有2张扑克牌,扑克牌上的数字如图所示.两人用这些扑克牌做游戏.他们先分别从自己的扑克牌中随机抽取一张,然后将他们抽出这两张扑克牌上的数字比较大小,数字大的一方获胜.请用画树状图(或列表)的方法,求小丹获胜的概率.
22.在一个不透明的袋子中有1个红球,2个白球和若干个黑球.小明将袋子中的球摇匀后,从中任意摸出一个球,记下颜色后放回袋中并摇匀,在多次重复以上操作后,小明统计了摸到红球的频率,并绘制了如折线统计图:
(1)袋子中一共有
个球;
(2)若从该袋中同时摸出2个球,求摸出的2个球都是白球的概率.
23.为了共同抗击“新冠”肺炎疫情,陕西某工程建筑队需要从工程技术部门中的5名技术人员(分别用A、B、C、D、E来表示)随机选取若干名技术人员参加“方舱医院”的建设,且每名技术人员被选中的可能性都相同.
(1)若随机选取一名技术人员去参加方舱医院的建设,则A技术员被选中的概率是多少?
(2)若随机选取两名技术人员去参加方舱医院的建设,则A、C技术员同被时选中的概率是多少?(请用树状图或列表法解答)
24.某校组织开展运动会,小明和扎西两名同学准备从100米短跑(记为项目A),800米中长跑(记为项目B),跳远(记为项目C),跳高(记为项目D),即从A,B,C,D四个项目中,分别选择一个项目参加比赛.请用画树状图或列表法求两名同学选到相同项目的概率.
25.某市林业局要移植一种树苗.对附近地区去年这种树苗移植成活的情况进行调查统计,并绘制了如图折线统计图:
(1)这种树苗成活概率的估计值为
.
(2)若移植这种树苗6000棵,估计可以成活
棵.
(3)若计划成活9000棵这种树苗,则需移植这种树苗大约多少棵?
26.某公司有甲、乙、丙三辆车去南京,它们出发的先后顺序随机.张先生和李先生乘坐该公司的车去南京出差,但有不同的需求.
请用所学概率知识解决下列问题:
(1)写出这三辆车按先后顺序出发的所有可能结果;
(2)两人中,谁乘坐到甲车的可能性大?请说明理由.
参考答案
一.选择题
1.
B.
2.
B.
3.
C.
4.
A.
5.
D.
6.
D.
7.
D.
8.
B.
9.
B.
10.
C.
11.
C.
12.
A.
二.填空题
13.
.
14.
0.94.
15.
.
16.
.
17.
30.
18.
.
三.解答题
19.
.
20.解:(1)10÷25%=40,
所以八年级一班一共有40名学生;
(2)阅读“小说”的人数为0.5×40=20(人);
阅读“戏剧”的人数的频率为=0.1;
阅读其它的人数的频率为=0.15;
在扇形统计图中,“戏剧”类对应的扇形圆形角的度数为360°×=36°;
故答案为20;0.1;0.15;
(3)画树状图为:
共有12种等可能的结果,其中选取的2人恰好是甲和丙的结果数为2,
所以选取的2人恰好是甲和丙的概率==.
21.解:画树状图得:
∵共有6种等可能的结果,小丹获胜的情况有3种,
∴P(小丹获胜)==.
22.解:(1)观察折线统计图可知:
摸到红球的频率稳定在0.2,
设袋子中有x个黑球,
所以=0.2,
解得x=2,
所以袋子中一共有5个球.
故答案为:5;
(2)解:将2个白球分别记作“白1”、“白2”,
2个黑球分别记作“黑1”、“黑2”.
从袋中同时摸出2个球,
可能出现的结果有10种,
即(红,白1),(红,白2),(红,黑1),(红,黑2),(白1,白2),(白1,黑1),(白1,黑2),(白2,黑1),(白2,黑2),(黑1,黑2),
并且它们出现的可能性相同.
其中2个球都是白球(记为事件A)的结果有1种,即(白1,白2),
所以P(A)=.
23.解:(1)A技术员被选中的概率为;
(2)画树状图为:
共有20种等可能的结果,其中A、C技术员同被时选中的结果数为2,
所以A、C技术员同被时选中的概率==.
24.解:画树状图得:
∵共有16种等可能的结果,两名同学选到相同项目的为4种情况,
∴P(两名同学选到相同项目)==.
25.解:(1)从折线统计图中的发展趋势,随着实验次数的增加,频率越稳定在0.9附近波动,根据频率估计概率,这种树苗成活概率约为0.9,
故答案为:0.9;
(2)6000×0.9=5400(棵),
故答案为:5400;
(3)9
000÷0.9=10000(棵),
答:需移植这种树苗大约10000棵.
26.解:(1)甲、乙、丙;甲、丙、乙;乙、甲、丙;乙、丙、甲;丙、甲、乙;丙、乙、甲;共6种;
(2)由(1)可知张先生坐到甲车有两种可能,乙、丙、甲,丙、乙、甲,
则张先生坐到甲车的概率是=;
由(1)可知李先生坐到甲车有两种可能,甲、乙、丙,甲、丙、乙,
则李先生坐到甲车的概率是=;
所以两人坐到甲车的可能性一样.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
