苏科版八年级数学上册第2章轴对称图形专题训练(Word版 含解析)
文档属性
| 名称 | 苏科版八年级数学上册第2章轴对称图形专题训练(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 104.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-11 00:00:00 | ||
图片预览

文档简介
国庆训练专题《轴对称》卷
一.选择题(共4小题)
1.如图,在△ABC中,∠B=90°,AC=10,AD为此三角形的一条角平分线,若BD=3,则三角形ADC的面积为( )
A.3
B.10
C.12
D.15
2.如图,△ABC中,AB=AC,∠A=50°,P是△ABC内一点,且∠PBC=∠PCA,则∠BPC的度数等于( )
A.100°
B.115°
C.130°
D.140°
3.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A.变小
B.不变
C.变大
D.无法判断
4.如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为( )
A.5
B.6
C.7
D.8
第1题
第2题
第3题
第4题
二.填空题(共4小题)
5.已知等腰三角形的一个内角等于20°,则它的一个底角是
.
6.如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是
.
7.如图,在直角三角形ABC中,∠BCA=90°,BC=3,D为AB上一点,连接CD,如果三角形BCD沿直线CD翻折后,点B恰好与边AC的中点E重合,那么点D到直线AC的距离为
.
8.如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为2cm/s和1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为ts,则当t=
s时,△PBQ为直角三角形.
第6题
第7题
第8题
三.解答题(共4小题)
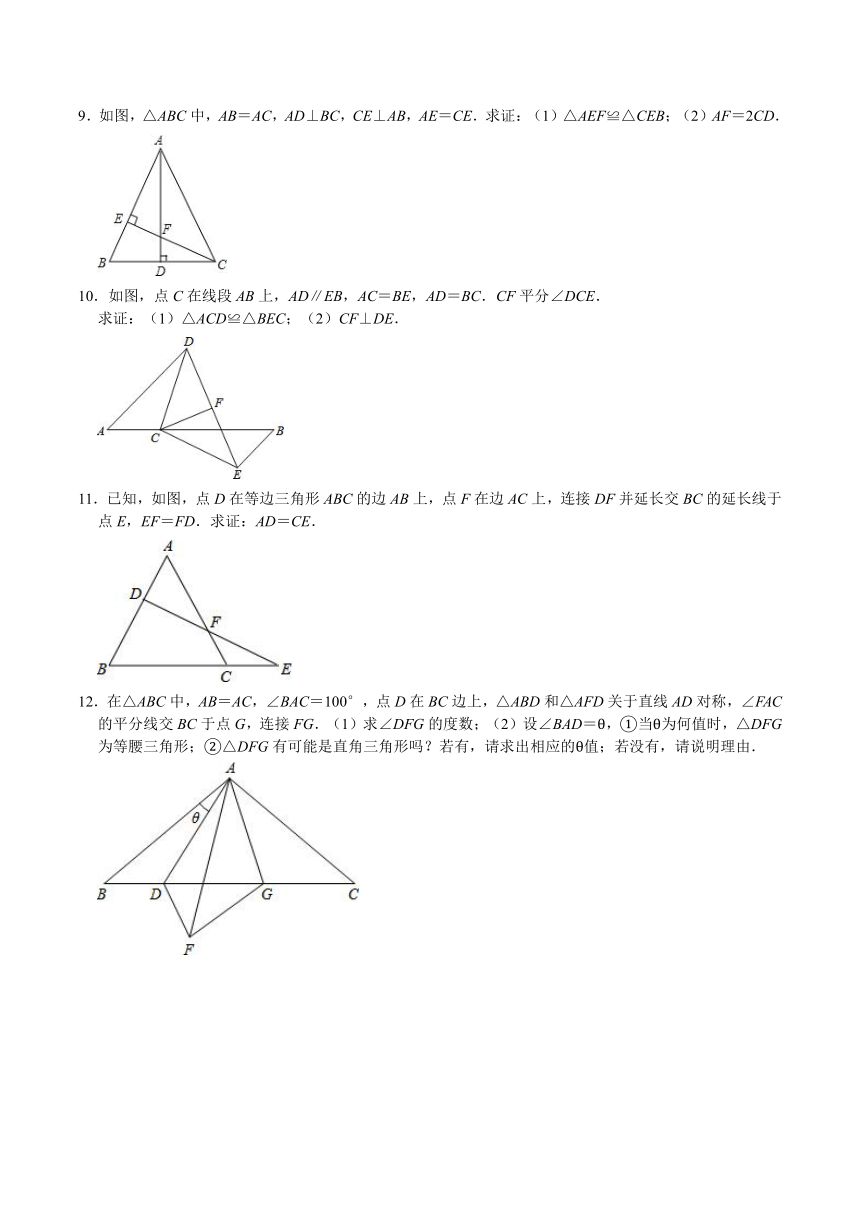
9.如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:(1)△AEF≌△CEB;(2)AF=2CD.
10.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;(2)CF⊥DE.
11.已知,如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD.求证:AD=CE.
12.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.(1)求∠DFG的度数;(2)设∠BAD=θ,①当θ为何值时,△DFG为等腰三角形;②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.
国庆训练专题轴对称卷参考答案与试题解析
一.选择题(共4小题)
1.【解答】解:过D作DE⊥AC于E.
∵AD是∠BAC的角平分线,∠B=90°(DB⊥AB),DE⊥AC,∴BD=DE,
∵BD=3,∴DE=3,∴S△ADC=?AC?DE=×10×3=15故选:D.
2.【解答】解:∵AB=AC,∠A=50°,∴∠ABC=∠ACB=65°.
∵∠PBC=∠PCA,∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(∠PCA+∠PCB)=180°﹣∠ACB=115°.故选:B.
3.【解答】解:在木棍滑动的过程中,点P到点O的距离不发生变化,
理由是:连接OP,
∵∠AOB=90°,P为AB中点,AB=2a,∴OP=AB=a,
即在木棍滑动的过程中,点P到点O的距离不发生变化,永远是a;故选:B.
4.【解答】解:∵在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,
∴∠B=∠C,∠BPE=∠EPC=90°,∴在直角△BPF和直角△EPC中有:∠BFP=∠E,
又∵∠BFP=∠EFA,∴∠E=∠EFA,∴AE=AF,
又∵AF=2,BF=3,AB=AC=AF+BF=2+3=5,AE=AF=2,∴CE=AE+AC=5+2=7,
故选:C.
二.填空题(共4小题)
5.【解答】解:当20°的角为等腰三角形的顶角时,底角的度数==80°;
当20°的角为等腰三角形的底角时,其底角为20°,故它的底角的度数是80°或20°.
故答案为:20°或80°.
6.【解答】解:∵在△ABC中,∠B与∠C的平分线交于点O,∴∠DBO=∠CBO,∠ECO=∠BCO,
∵DE∥BC,∴∠DOB=∠CBO,∠EOC=∠BCO,
∴∠DBO=∠DOB,∠ECO=∠EOC,∴OD=BD,OE=CE,
∵AB=5,AC=4,∴△ADE的周长为:AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+AC=5+4=9.故答案为:9.
7.【解答】解:过点D作DN⊥AC于N,过点D作DM⊥AB,
由折叠的性质可得:∠BCD=∠ACD,CE=CB=3,∴DM=DN,∵E是AC的中点,∴AC=2AE=6,
∵S△BAC=S△BCD+S△ACD,即CB?AC=BC?DM+AC?DN,∴×3×6=×DN×3+×6×DN,
解得:DN=2,∴点D到AC的距离是2.故答案为:2.
8.【解答】解:∵△ABC是等边三角形,∴AB=BC=6cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,∠BPQ=30°,∴BP=2BQ.∵BP=6﹣2x,BQ=x,∴6﹣2x=2x,解得x=;
当∠QPB=90°时,∠PQB=30°,∴BQ=2PB,∴x=2(6﹣2x),解得x=.
答:或秒时,△BPQ是直角三角形.故答案为或.
三.解答题(共4小题)
9.【解答】证明:(1)∵AD⊥BC,CE⊥AB,∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,∵∠CFD=∠AFE,∴∠AFE=∠B
在△AEF与△CEB中,,∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,∴BC=2CD,∵△AEF≌△CEB,∴AF=BC,∴AF=2CD.
10.【解答】证明:(1)∵AD∥BE,∴∠A=∠B,
在△ACD和△BEC中∴△ACD≌△BEC(SAS),
(2)∵△ACD≌△BEC,∴CD=CE,又∵CF平分∠DCE,∴CF⊥DE.
11.【解答】证明:作DG∥BC交AC于G,如图所示:则∠DGF=∠ECF,
在△DFG和△EFC中,,∴△DFG≌△EFC(AAS),∴GD=CE,
∵△ABC是等边三角形,∴∠A=∠B=∠ACB=60°,
∵DG∥BC,∴∠ADG=∠B,∠AGD=∠ACB,∴∠A=∠ADG=∠AGD,
∴△ADG是等边三角形,∴AD=GD,∴AD=CE.
12.【解答】解:(1)∵AB=AC,∠BAC=100°,∴∠B=∠C=40°.
∵△ABD和△AFD关于直线AD对称,∴△ADB≌△ADF,
∴∠B=∠AFD=40°,AB=AF∠BAD=∠FAD=θ,∴AF=AC.
∵AG平分∠FAC,∴∠FAG=∠CAG.
在△AGF和△AGC中,,∴△AGF≌△AGC(SAS),∴∠AFG=∠C.
∵∠DFG=∠AFD+∠AFG,∴∠DFG=∠B+∠C=40°+40°=80°.答:∠DFG的度数为80°;
(2)①当GD=GF时,∴∠GDF=∠GFD=80°.
∵∠ADG=40°+θ,∴40°+80°+40°+θ+θ=180°,∴θ=10°.
当DF=GF时,∴∠FDG=∠FGD.
∵∠DFG=80°,∴∠FDG=∠FGD=50°.∴40°+50°+40°+2θ=180°,∴θ=25°.
当DF=DG时,∴∠DFG=∠DGF=80°,∴∠GDF=20°,∴40°+20°+40°+2θ=180°,∴θ=40°.
∴当θ=10°,25°或40°时,△DFG为等腰三角形;
②当∠GDF=90°时,∵∠DFG=80°,∴40°+90°+40°+2θ=180°,∴θ=5°.
当∠DGF=90°时,∵∠DFG=80°,∴∠GDF=10°,∴40°+10°+40°+2θ=180°,∴θ=45°,
综上所述,当θ=5°或45°时,△DFG为直角三角形.
一.选择题(共4小题)
1.如图,在△ABC中,∠B=90°,AC=10,AD为此三角形的一条角平分线,若BD=3,则三角形ADC的面积为( )
A.3
B.10
C.12
D.15
2.如图,△ABC中,AB=AC,∠A=50°,P是△ABC内一点,且∠PBC=∠PCA,则∠BPC的度数等于( )
A.100°
B.115°
C.130°
D.140°
3.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A.变小
B.不变
C.变大
D.无法判断
4.如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,BF=3,则CE的长度为( )
A.5
B.6
C.7
D.8
第1题
第2题
第3题
第4题
二.填空题(共4小题)
5.已知等腰三角形的一个内角等于20°,则它的一个底角是
.
6.如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是
.
7.如图,在直角三角形ABC中,∠BCA=90°,BC=3,D为AB上一点,连接CD,如果三角形BCD沿直线CD翻折后,点B恰好与边AC的中点E重合,那么点D到直线AC的距离为
.
8.如图,△ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为2cm/s和1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为ts,则当t=
s时,△PBQ为直角三角形.
第6题
第7题
第8题
三.解答题(共4小题)
9.如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:(1)△AEF≌△CEB;(2)AF=2CD.
10.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;(2)CF⊥DE.
11.已知,如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD.求证:AD=CE.
12.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.(1)求∠DFG的度数;(2)设∠BAD=θ,①当θ为何值时,△DFG为等腰三角形;②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.
国庆训练专题轴对称卷参考答案与试题解析
一.选择题(共4小题)
1.【解答】解:过D作DE⊥AC于E.
∵AD是∠BAC的角平分线,∠B=90°(DB⊥AB),DE⊥AC,∴BD=DE,
∵BD=3,∴DE=3,∴S△ADC=?AC?DE=×10×3=15故选:D.
2.【解答】解:∵AB=AC,∠A=50°,∴∠ABC=∠ACB=65°.
∵∠PBC=∠PCA,∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(∠PCA+∠PCB)=180°﹣∠ACB=115°.故选:B.
3.【解答】解:在木棍滑动的过程中,点P到点O的距离不发生变化,
理由是:连接OP,
∵∠AOB=90°,P为AB中点,AB=2a,∴OP=AB=a,
即在木棍滑动的过程中,点P到点O的距离不发生变化,永远是a;故选:B.
4.【解答】解:∵在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,
∴∠B=∠C,∠BPE=∠EPC=90°,∴在直角△BPF和直角△EPC中有:∠BFP=∠E,
又∵∠BFP=∠EFA,∴∠E=∠EFA,∴AE=AF,
又∵AF=2,BF=3,AB=AC=AF+BF=2+3=5,AE=AF=2,∴CE=AE+AC=5+2=7,
故选:C.
二.填空题(共4小题)
5.【解答】解:当20°的角为等腰三角形的顶角时,底角的度数==80°;
当20°的角为等腰三角形的底角时,其底角为20°,故它的底角的度数是80°或20°.
故答案为:20°或80°.
6.【解答】解:∵在△ABC中,∠B与∠C的平分线交于点O,∴∠DBO=∠CBO,∠ECO=∠BCO,
∵DE∥BC,∴∠DOB=∠CBO,∠EOC=∠BCO,
∴∠DBO=∠DOB,∠ECO=∠EOC,∴OD=BD,OE=CE,
∵AB=5,AC=4,∴△ADE的周长为:AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+AC=5+4=9.故答案为:9.
7.【解答】解:过点D作DN⊥AC于N,过点D作DM⊥AB,
由折叠的性质可得:∠BCD=∠ACD,CE=CB=3,∴DM=DN,∵E是AC的中点,∴AC=2AE=6,
∵S△BAC=S△BCD+S△ACD,即CB?AC=BC?DM+AC?DN,∴×3×6=×DN×3+×6×DN,
解得:DN=2,∴点D到AC的距离是2.故答案为:2.
8.【解答】解:∵△ABC是等边三角形,∴AB=BC=6cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,∠BPQ=30°,∴BP=2BQ.∵BP=6﹣2x,BQ=x,∴6﹣2x=2x,解得x=;
当∠QPB=90°时,∠PQB=30°,∴BQ=2PB,∴x=2(6﹣2x),解得x=.
答:或秒时,△BPQ是直角三角形.故答案为或.
三.解答题(共4小题)
9.【解答】证明:(1)∵AD⊥BC,CE⊥AB,∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,∵∠CFD=∠AFE,∴∠AFE=∠B
在△AEF与△CEB中,,∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,∴BC=2CD,∵△AEF≌△CEB,∴AF=BC,∴AF=2CD.
10.【解答】证明:(1)∵AD∥BE,∴∠A=∠B,
在△ACD和△BEC中∴△ACD≌△BEC(SAS),
(2)∵△ACD≌△BEC,∴CD=CE,又∵CF平分∠DCE,∴CF⊥DE.
11.【解答】证明:作DG∥BC交AC于G,如图所示:则∠DGF=∠ECF,
在△DFG和△EFC中,,∴△DFG≌△EFC(AAS),∴GD=CE,
∵△ABC是等边三角形,∴∠A=∠B=∠ACB=60°,
∵DG∥BC,∴∠ADG=∠B,∠AGD=∠ACB,∴∠A=∠ADG=∠AGD,
∴△ADG是等边三角形,∴AD=GD,∴AD=CE.
12.【解答】解:(1)∵AB=AC,∠BAC=100°,∴∠B=∠C=40°.
∵△ABD和△AFD关于直线AD对称,∴△ADB≌△ADF,
∴∠B=∠AFD=40°,AB=AF∠BAD=∠FAD=θ,∴AF=AC.
∵AG平分∠FAC,∴∠FAG=∠CAG.
在△AGF和△AGC中,,∴△AGF≌△AGC(SAS),∴∠AFG=∠C.
∵∠DFG=∠AFD+∠AFG,∴∠DFG=∠B+∠C=40°+40°=80°.答:∠DFG的度数为80°;
(2)①当GD=GF时,∴∠GDF=∠GFD=80°.
∵∠ADG=40°+θ,∴40°+80°+40°+θ+θ=180°,∴θ=10°.
当DF=GF时,∴∠FDG=∠FGD.
∵∠DFG=80°,∴∠FDG=∠FGD=50°.∴40°+50°+40°+2θ=180°,∴θ=25°.
当DF=DG时,∴∠DFG=∠DGF=80°,∴∠GDF=20°,∴40°+20°+40°+2θ=180°,∴θ=40°.
∴当θ=10°,25°或40°时,△DFG为等腰三角形;
②当∠GDF=90°时,∵∠DFG=80°,∴40°+90°+40°+2θ=180°,∴θ=5°.
当∠DGF=90°时,∵∠DFG=80°,∴∠GDF=10°,∴40°+10°+40°+2θ=180°,∴θ=45°,
综上所述,当θ=5°或45°时,△DFG为直角三角形.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
