上海中学2021届高三上学期数学周测卷01 Word版含答案
文档属性
| 名称 | 上海中学2021届高三上学期数学周测卷01 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 428.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 18:57:33 | ||
图片预览

文档简介
1029970011239500
2020-2021学年上海中学高三上数学周测卷01 2020.09
一. 填空题
1. 函数false的定义域为
2. 复数false的实部为
3. 计算:false
4. 已知等比数列false各项均为正数,满足false,false,则公比false
5. 已知false是定义在false上的周期为3的奇函数,且false,则false的值为
6. 已知向量,,则在上的投影为
7. 函数false(false)的单调递增区间为
8. 已知false为有理数集,设集合false,在下列集合中:
① false;② false;③ false;④ false;
与false相等的集合的序号是
9. 设函数false(false),若关于false的方程false在区间false上有且仅有两个不相等的实根,则false的最大整数值为
10. 已知正数false、false满足false,若false恒成立,则实数false的取值范围是
11. 已知false,函数false的最小值为false,则false的取值范围是
48609253619512. 已知集合false,由集合false中
所有的点组成的图形如图中阴影部分所示,中间白色部分形如美丽的“水滴”,
给出下列结论:
①“水滴”图形与false轴相交,最高点记为false,则点false的坐标为false;
② 在集合false中任取一点false,则false到原点的距离的最大值为4;
③ 阴影部分与false轴相交,最高点和最低点分别记为false、false,则false;
其中正确的序号是
二. 选择题
13. 设、是非零向量,则“、共线”是“”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既非充分也非必要条件
14. 设函数false,则“false”是“false的最小正周期为false”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
15. 当急需住院人数超过医院所能收治的病人数量时就会发生“医疗资源挤兑”现象,在新冠肺炎爆发期间,境外某市每日下班后统计住院人数,从中发现:该市每日因新冠肺炎住院人数均比前一天下班后统计的住院人数增加约25%,但每日大约有200名新冠肺炎患者治愈出院,已知该市某天下班后有1000名新冠肺炎患者住院治疗,
该市的医院共可收治4000名新冠肺炎患者,若继续按照这样的规律发展,该市因新冠肺炎疫情发生“医疗资源
挤兑”现象只需要约( )A. 7天 B. 10天 C. 13天 D. 16天
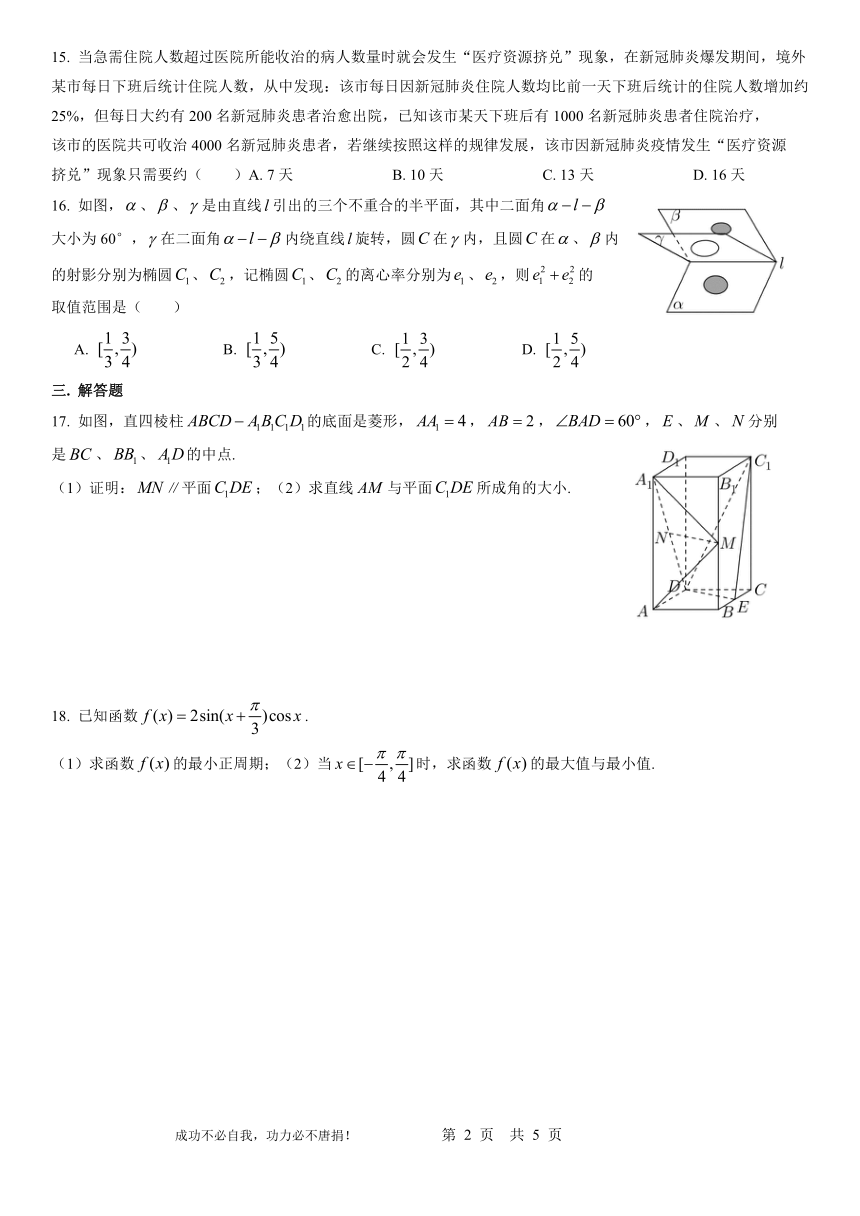
513143511112516. 如图,false、false、false是由直线false引出的三个不重合的半平面,其中二面角false
大小为60°,false在二面角false内绕直线false旋转,圆false在false内,且圆false在false、false内
的射影分别为椭圆false、false,记椭圆false、false的离心率分别为false、false,则false的
取值范围是( )
A. false B. false C. false D. false
三. 解答题
513143535052017. 如图,直四棱柱false的底面是菱形,false,false,false,false、false、false分别
是false、false、false的中点.
(1)证明:false∥平面false;(2)求直线false与平面false所成角的大小.
18. 已知函数false.
(1)求函数false的最小正周期;(2)当false时,求函数false的最大值与最小值.
19. 有一条长为120米的步行道false,false是垃圾投放点false,若以false为原点,false为false轴正半轴建立直角坐标系,
设点false,现要建设另一座垃圾投放点false,函数false表示与false点距离最近的垃圾投放点的距离.
(1)若false,求false、false、false的值,并写出false的函数解析式;
(2)若可以通过false与坐标轴围成的面积来测算扔垃圾的便利程度,面积越小越便利,问:垃圾投放点false建
在何处才能比建在中点时更加便利?
20. 已知椭圆false(false,false)的左右焦点分别为false、false,过false的直线false交椭圆false于false、false
两点,其中△false的周长为16,且当false与false轴垂直时,false的长为2.(1)求椭圆false的标准方程;
(2)当false时,点false在false轴上方,求点false的坐标;
(3)若直线false交false轴于false,直线false交false轴于false,是否存在直线false,使得△false的面积与△false的面积
4614545173990相等?若存在,求出直线false的方程,若不存在,请说明理由.
21. 设false为正整数,各项均为正整数的数列false定义如下:false,false.
(1)若false,写出false、false、false;
(2)求证:数列false单调递增的充要条件是false为偶数;
(3)若false为奇数,是否存在false满足false?请说明理由.
2020上海中学高三上数学周测卷01参考答案
一. 填空题
1. false 2. false 3. false 4. false 5. false
6. false 7. false 8. ①②④
9. false 10. false 11. false 12. ①③
二. 选择题
13. B 14. C 15. C 16. C
三. 解答题
17.(1)证明略;(2)false.
18.(1)false;(2)false,false.
19.(1)投放点false,false,false表示与false距离最近的投放点(即false)的距离,∴false,同理分析,false,
false. 由题意,false,∴分类讨论,
当false,即false时,false;当false,
即false时,false;综上,false
(2)由题意,false,∴false,
327660088900false与坐标轴围成的面积如阴影部分所示,
∴false,
由题意,false,即false,
解得false,即垃圾投放点false建在false与false之间时,比建在中点时更加便利
20.(1)false;(2)false;(3)false.
21.(1)6、3、8;(2)证明略;(3)存在.
2020-2021学年上海中学高三上数学周测卷01 2020.09
一. 填空题
1. 函数false的定义域为
2. 复数false的实部为
3. 计算:false
4. 已知等比数列false各项均为正数,满足false,false,则公比false
5. 已知false是定义在false上的周期为3的奇函数,且false,则false的值为
6. 已知向量,,则在上的投影为
7. 函数false(false)的单调递增区间为
8. 已知false为有理数集,设集合false,在下列集合中:
① false;② false;③ false;④ false;
与false相等的集合的序号是
9. 设函数false(false),若关于false的方程false在区间false上有且仅有两个不相等的实根,则false的最大整数值为
10. 已知正数false、false满足false,若false恒成立,则实数false的取值范围是
11. 已知false,函数false的最小值为false,则false的取值范围是
48609253619512. 已知集合false,由集合false中
所有的点组成的图形如图中阴影部分所示,中间白色部分形如美丽的“水滴”,
给出下列结论:
①“水滴”图形与false轴相交,最高点记为false,则点false的坐标为false;
② 在集合false中任取一点false,则false到原点的距离的最大值为4;
③ 阴影部分与false轴相交,最高点和最低点分别记为false、false,则false;
其中正确的序号是
二. 选择题
13. 设、是非零向量,则“、共线”是“”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既非充分也非必要条件
14. 设函数false,则“false”是“false的最小正周期为false”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
15. 当急需住院人数超过医院所能收治的病人数量时就会发生“医疗资源挤兑”现象,在新冠肺炎爆发期间,境外某市每日下班后统计住院人数,从中发现:该市每日因新冠肺炎住院人数均比前一天下班后统计的住院人数增加约25%,但每日大约有200名新冠肺炎患者治愈出院,已知该市某天下班后有1000名新冠肺炎患者住院治疗,
该市的医院共可收治4000名新冠肺炎患者,若继续按照这样的规律发展,该市因新冠肺炎疫情发生“医疗资源
挤兑”现象只需要约( )A. 7天 B. 10天 C. 13天 D. 16天
513143511112516. 如图,false、false、false是由直线false引出的三个不重合的半平面,其中二面角false
大小为60°,false在二面角false内绕直线false旋转,圆false在false内,且圆false在false、false内
的射影分别为椭圆false、false,记椭圆false、false的离心率分别为false、false,则false的
取值范围是( )
A. false B. false C. false D. false
三. 解答题
513143535052017. 如图,直四棱柱false的底面是菱形,false,false,false,false、false、false分别
是false、false、false的中点.
(1)证明:false∥平面false;(2)求直线false与平面false所成角的大小.
18. 已知函数false.
(1)求函数false的最小正周期;(2)当false时,求函数false的最大值与最小值.
19. 有一条长为120米的步行道false,false是垃圾投放点false,若以false为原点,false为false轴正半轴建立直角坐标系,
设点false,现要建设另一座垃圾投放点false,函数false表示与false点距离最近的垃圾投放点的距离.
(1)若false,求false、false、false的值,并写出false的函数解析式;
(2)若可以通过false与坐标轴围成的面积来测算扔垃圾的便利程度,面积越小越便利,问:垃圾投放点false建
在何处才能比建在中点时更加便利?
20. 已知椭圆false(false,false)的左右焦点分别为false、false,过false的直线false交椭圆false于false、false
两点,其中△false的周长为16,且当false与false轴垂直时,false的长为2.(1)求椭圆false的标准方程;
(2)当false时,点false在false轴上方,求点false的坐标;
(3)若直线false交false轴于false,直线false交false轴于false,是否存在直线false,使得△false的面积与△false的面积
4614545173990相等?若存在,求出直线false的方程,若不存在,请说明理由.
21. 设false为正整数,各项均为正整数的数列false定义如下:false,false.
(1)若false,写出false、false、false;
(2)求证:数列false单调递增的充要条件是false为偶数;
(3)若false为奇数,是否存在false满足false?请说明理由.
2020上海中学高三上数学周测卷01参考答案
一. 填空题
1. false 2. false 3. false 4. false 5. false
6. false 7. false 8. ①②④
9. false 10. false 11. false 12. ①③
二. 选择题
13. B 14. C 15. C 16. C
三. 解答题
17.(1)证明略;(2)false.
18.(1)false;(2)false,false.
19.(1)投放点false,false,false表示与false距离最近的投放点(即false)的距离,∴false,同理分析,false,
false. 由题意,false,∴分类讨论,
当false,即false时,false;当false,
即false时,false;综上,false
(2)由题意,false,∴false,
327660088900false与坐标轴围成的面积如阴影部分所示,
∴false,
由题意,false,即false,
解得false,即垃圾投放点false建在false与false之间时,比建在中点时更加便利
20.(1)false;(2)false;(3)false.
21.(1)6、3、8;(2)证明略;(3)存在.
同课章节目录
