2019-2020学年山东省青岛市平度市国开中学七年级下学期期中数学试卷 (word,解析版)
文档属性
| 名称 | 2019-2020学年山东省青岛市平度市国开中学七年级下学期期中数学试卷 (word,解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 753.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 05:23:26 | ||
图片预览




文档简介
2019-2020学年山东省青岛市平度市国开中学七年级第二学期期中数学试卷
一、选择题(共8小题).
1.(3分)下列运算中,正确的是( )
A.a2+a3=a5 B.a6÷a3=a2 C.(a4)2=a6 D.a2?a3=a5
2.(3分)下列四个图形中,∠1和∠2是同位角的是( )
A. B.
C. D.
3.(3分)下列各式中,不能应用平方差公式进行计算的是( )
A.(﹣x+2y)(2y+x) B.(x+y)(x﹣y)
C.(a﹣b)(﹣a+b) D.(﹣2m+n)(﹣2m﹣n)
4.(3分)已知一个等腰三角形的两边长分别是2和5,那么这个等腰三角形的周长为( )
A.9 B.12 C.9或12 D.7
5.(3分)如图,下列推理不正确的是( )
A.∵AB∥CD,∴∠ABC+∠C=180° B.∵∠1=∠2,∴AD∥BC
C.∵AD∥BC,∴∠3=∠4 D.∵∠A+∠ADC=180°,∴AB∥CD
6.(3分)如图,表示某港口某日从6时到18时水深变化情况,每一艘轮船在水深不低于6米时可安全通航,满足这一要求的时间段是( )
A.12小时以后 B.14小时以后 C.10时到14时 D.12时到16时
7.(3分)下列说法正确的有( )
①等角的余角相等;②过一点有且只有一条直线与已知直线平行;③相等的角是对顶角;
④同位角相等;⑤过直线外一点做这条直线的垂线段,则这条垂线段叫做这个点到这条直线的距离.
A.1个 B.2个 C.3个 D.4个
8.(3分)我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(1)可以用来解释(a+b)2﹣(a﹣b)2=4ab.那么通过图(2)面积的计算,验证了一个恒等式,此等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.(a﹣b)(a+2b)=a2+ab﹣b2
二.填空题(本题满分24分,共8小题,每小题3分)
9.(3分)生物具有遗传多样性,遗传信息大多储存在DNA分子上,一个DNA分子的直径约为0.0000002cm.这个数量用科学记数法可表示为 cm.
10.(3分)计算32013×()2015的结果是 .
11.(3分)填空:x2﹣10x+ =( )2.
12.(3分)如图,直角三角形ABC中,AC⊥BC,CD⊥AB,点A到直线BC的距离等于线段 的长度,点A到直线CD的距离等于线段 的长度.
13.(3分)BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是 .
14.(3分)声音在空气中的传播速度v(m/s)与温度t(℃)的关系如表:
温度(℃) 0 5 10 15 20
速度v(m/s) 331 336 341 346 351
则速度v与温度t之间的关系式为 ;当t=30℃时,声音的传播速度为 m/s.
15.(3分)某人从A点出发向北偏东60°方向前进到达B点,再从B点出发向南偏西15°方向前进到达C点,则∠ABC= °.
16.(3分)观察下列各式:
13+23=9=×4×9=×22×32
13+23+33=36=×9×16=×32×42
13+23+33+43=100=×16×25=×42×52
若n为正整数,试猜想13+23+33+…+n3等于 .(注:最终结果保留带括号的形式即可)
三.作图题(本题满分4分)
17.(4分)用圆规、直尺作图,不写作法,但保留作图痕迹.
一木匠师傅打算在长方形木板上截一个平行四边形使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB,另一边过点C,且与AB平行,请帮忙确定这条边.
四.解答题
18.(16分)计算:
(1)﹣20+4﹣1×(﹣1)2008×()﹣2;
(2)(2x+1)(2x﹣1)﹣(2x+1)2;
(3)(a+3b﹣2c)(a﹣3b﹣2c);
(4)103×97(运用公式简算).
19.(6分)先化简,后求值:
(2x﹣3)2﹣(x+2y)(x﹣2y)﹣4y2,其中x=1,y=3.
20.(5分)已知:如图AB⊥BC于B,CD⊥BC于C,∠1=∠2.求证:BE∥CF.
证明:∵AB⊥BC,CD⊥BC(已知)
∴∠ABC=90°,∠BCD=90°( )
即∠1+∠3=90°,∠2+∠4=90°
又∵∠1=∠2( )
∴ = ( )
∴BE∥CF( )
21.(6分)周老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000
米.一天,周老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.周老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)求a的值.
(2)b= ;c= .
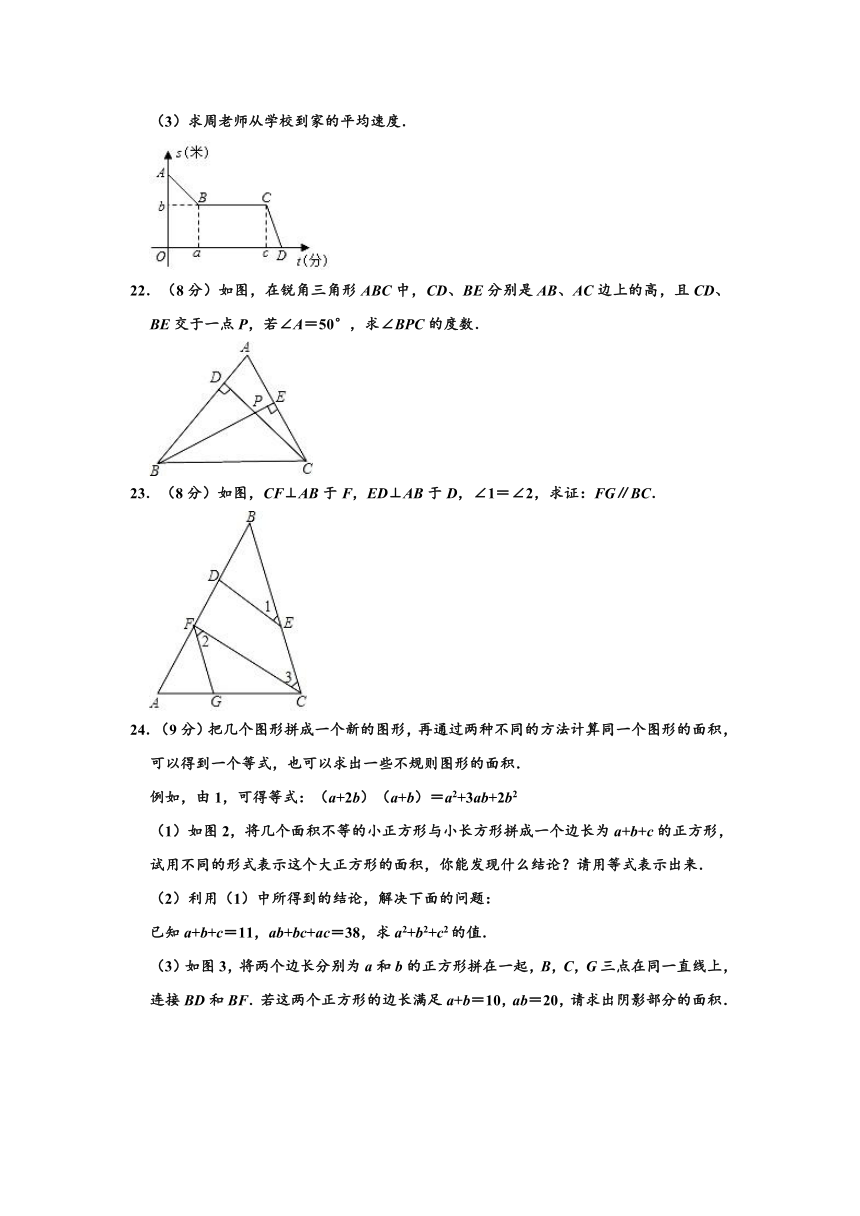
(3)求周老师从学校到家的平均速度.
22.(8分)如图,在锐角三角形ABC中,CD、BE分别是AB、AC边上的高,且CD、BE交于一点P,若∠A=50°,求∠BPC的度数.
23.(8分)如图,CF⊥AB于F,ED⊥AB于D,∠1=∠2,求证:FG∥BC.
24.(9分)把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
25.(10分)已知直线l1∥l2,且l4和l1、l2分别交于A、B两点,点P为线段AB上的一个定点(如图1)
(1)写出∠1、∠2、∠3、之间的关系并说出理由.
(2)如果点P为线段AB上的动点时,问∠1、∠2、∠3之间的关系是否发生变化?(不必说理由)
(3)如果点P在A、B两点外侧运动时,(点P和点A、点B不重合)
①如图2,当点P在射线AB上运动时,∠1、∠2、∠3之间关系并说出理由.
②如图3,当点P在射线BA上运动时,∠1、∠2、∠3之间关系(不必说理由).
参考答案
一.选择题(本题满分24分,共8小题,每小题3分)
1.(3分)下列运算中,正确的是( )
A.a2+a3=a5 B.a6÷a3=a2 C.(a4)2=a6 D.a2?a3=a5
【分析】根据合并同类项法则,同底数幂相除,底数不变指数相减;幂的乘方,底数不变指数相乘;同底数幂相乘,底数不变指数相加,对各选项分析判断后利用排除法求解.
解:A、a2与a3不是同类项,不能合并,故本选项错误;
B、a6÷a3=a3,故本选项错误;
C、(a4)2=a8,故本选项错误;
D、a2?a3=a5,故本选项正确.
故选:D.
2.(3分)下列四个图形中,∠1和∠2是同位角的是( )
A. B.
C. D.
【分析】同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角.
解:A图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角;
B图中,∠1与∠2的两边都不在同一条直线上,不是同位角;
C图中,∠1与∠2有一条边在同一条直线上,另一条边不在被截线的同一方,不是同位角;
D图中,∠1与∠2有一条边在同一条直线上,另一条边不在被截线的同一方,不是同位角.
故选:A.
3.(3分)下列各式中,不能应用平方差公式进行计算的是( )
A.(﹣x+2y)(2y+x) B.(x+y)(x﹣y)
C.(a﹣b)(﹣a+b) D.(﹣2m+n)(﹣2m﹣n)
【分析】利用平方差公式和完全平方公式对各选项进行判断.
解:(﹣x+2y)(2y+x)=(2y﹣x)(2y+x)=4y2﹣x2;
(x+y)(x﹣y)=x2﹣y2;
(a﹣b)(﹣a+b)=﹣(a﹣b)(a﹣b)=﹣(a﹣b)2=﹣a2+2ab+b2,
(﹣2m+n)(﹣2m﹣n)=(﹣2m)2﹣n2=4m2﹣n2.
故选:C.
4.(3分)已知一个等腰三角形的两边长分别是2和5,那么这个等腰三角形的周长为( )
A.9 B.12 C.9或12 D.7
【分析】题目给出等腰三角形有两条边长为2和5,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解:分两种情况:
当腰为2时,2+2<5,所以不能构成三角形;
当腰为5时,2+5>5,所以能构成三角形,周长是:2+5+5=12.
故选:B.
5.(3分)如图,下列推理不正确的是( )
A.∵AB∥CD,∴∠ABC+∠C=180° B.∵∠1=∠2,∴AD∥BC
C.∵AD∥BC,∴∠3=∠4 D.∵∠A+∠ADC=180°,∴AB∥CD
【分析】根据平行线的判定和性质逐项判断即可.
解:A、由AB∥CD,根据平行线的性质可得到∠ABC+∠BCD=180°,所以A正确;
B、由∠1=∠2可判定AD∥BC,所以B正确;
C、由AD∥BC,根据两直线平行,内错角相等可得到∠1=∠2,所以C不正确;
D、由∠A+∠ADC=180°,根据同旁内角互补两直线平行可得到AB∥CD,所以D正确;
故选:C.
6.(3分)如图,表示某港口某日从6时到18时水深变化情况,每一艘轮船在水深不低于6米时可安全通航,满足这一要求的时间段是( )
A.12小时以后 B.14小时以后 C.10时到14时 D.12时到16时
【分析】从图象上找到当水深为6米及6米以上的时间即可得到本题的答案.
解:∵当船底与水底间的距离不少于6米时,才能安全通过.
从图象可知水深为6米的时间为12时到16时,
故选:D.
7.(3分)下列说法正确的有( )
①等角的余角相等;②过一点有且只有一条直线与已知直线平行;③相等的角是对顶角;
④同位角相等;⑤过直线外一点做这条直线的垂线段,则这条垂线段叫做这个点到这条直线的距离.
A.1个 B.2个 C.3个 D.4个
【分析】根据平行线的性质、余角和补角的性质、点到直线的距离、对顶角的性质以及平行公理及推论即可判断.
解:①等角的余角相等,故此说法正确;
②过直线外一点有且只有一条直线与已知直线平行,故此说法错误;
③相等的角不一定是对顶角,故此说法错误;
④两直线平行,同位角相等,故此说法错误;
⑤过直线外一点做这条直线的垂线段,则这条垂线段叫做这个点到这条直线的距离,故此说法正确;
故选:B.
8.(3分)我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(1)可以用来解释(a+b)2﹣(a﹣b)2=4ab.那么通过图(2)面积的计算,验证了一个恒等式,此等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.(a﹣b)(a+2b)=a2+ab﹣b2
【分析】图(1)求的是阴影部分的面积,同样,图(2)正方形的面积用代数式表示即可.
解:图(2)中,
∵S空白正方形=a2﹣2b(a﹣b)﹣b2=a2﹣2ab+b2=(a﹣b)2,
∴(a﹣b)2=a2﹣2ab+b2.
故选:B.
二.填空题(本题满分24分,共8小题,每小题3分)
9.(3分)生物具有遗传多样性,遗传信息大多储存在DNA分子上,一个DNA分子的直径约为0.0000002cm.这个数量用科学记数法可表示为 2×10﹣7 cm.
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n.与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.在本题中a应为2,10的指数为﹣7.
解:0.000 000 2cm=2×10﹣7cm.
故答案为:2×10﹣7.
10.(3分)计算32013×()2015的结果是 .
【分析】根据积的乘方运算法则解答即可.
解:32013×()2015
=32013×()2013×
=×
=,
故答案为:.
11.(3分)填空:x2﹣10x+ 25 =( 5 )2.
【分析】根据完全平方公式解答即可.
解:x2﹣10x+()2=(x﹣)2,即x2﹣10x+25=(x﹣5)2,
故答案为:25;5.
12.(3分)如图,直角三角形ABC中,AC⊥BC,CD⊥AB,点A到直线BC的距离等于线段 AC 的长度,点A到直线CD的距离等于线段 AD 的长度.
【分析】利用点到直线的距离可得答案.
解:直角三角形ABC中,AC⊥BC,CD⊥AB,点A到直线BC的距离等于线段AC的长度,点A到直线CD的距离等于线段AD的长度.
故答案为:AC;AD.
13.(3分)BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是 2 .
【分析】根据三角形的中线的定义可得AD=CD,再求出△ABD和△BCD的周长的差=AB﹣BC.
解:∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长的差=(AB+BD+AD)﹣(BC+BD+CD)=AB﹣BC,
∵AB=5,BC=3,
∴△ABD和△BCD的周长的差=5﹣3=2.
故答案为:2.
14.(3分)声音在空气中的传播速度v(m/s)与温度t(℃)的关系如表:
温度(℃) 0 5 10 15 20
速度v(m/s) 331 336 341 346 351
则速度v与温度t之间的关系式为 v=t+331 ;当t=30℃时,声音的传播速度为 361 m/s.
【分析】根据表格中两个变量的变化规律,得出速度与温度之间变化的关系式,再代入求函数值即可.
解:根据表格中两个变量的变化规律可得,v=t+331;
当t=30时,v=30+331=361(m/s),
故答案为:v=t+331,361.
15.(3分)某人从A点出发向北偏东60°方向前进到达B点,再从B点出发向南偏西15°方向前进到达C点,则∠ABC= 45 °.
【分析】根据方向角的定义即可作出判断.
解:∠ABC=60°﹣15°=45°.
故答案是:45.
16.(3分)观察下列各式:
13+23=9=×4×9=×22×32
13+23+33=36=×9×16=×32×42
13+23+33+43=100=×16×25=×42×52
若n为正整数,试猜想13+23+33+…+n3等于 n2(n+1)2 .(注:最终结果保留带括号的形式即可)
【分析】由所给的数据,得出变化规律,即是乘以最后一个数的平方,再乘以最后一个数加1的平方,即可得出答案.
解:根据题意得,13+23+33+4+…+n3=n2(n+1)2.
故答案为n2(n+1)2.
三.作图题(本题满分4分)
17.(4分)用圆规、直尺作图,不写作法,但保留作图痕迹.
一木匠师傅打算在长方形木板上截一个平行四边形使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB,另一边过点C,且与AB平行,请帮忙确定这条边.
【分析】在射线BE上截取DB,使得BD=AC,作直线CD即可,四边形ABDC即为所求.
解:如图,平行四边形ABDC即为所求.
四.解答题
18.(16分)计算:
(1)﹣20+4﹣1×(﹣1)2008×()﹣2;
(2)(2x+1)(2x﹣1)﹣(2x+1)2;
(3)(a+3b﹣2c)(a﹣3b﹣2c);
(4)103×97(运用公式简算).
【分析】(1)根据零指数幂、负整数指数幂、有理数的乘方的运算法则进行计算即可;
(2)用平方差公式和完全平方公式将式子展开后进行合并即可;
(3)可用平方差公式和完全平方公式进行计算即可;
(4)利用平方差公式计算即可.
解:(1)原式=﹣1+0.25×1×4
=﹣1+1
=0;
(2)原式=4x2﹣1﹣(4x2+4x+1)
=4x2﹣1﹣4x2﹣4x﹣1
=﹣4x﹣2;
(3)原式=(a﹣2c)2﹣9b2
=a2﹣4ac+4c2﹣9b2;
(4)原式=(100+3)×(100﹣3)
=1002﹣32
=10000﹣9
=9991.
19.(6分)先化简,后求值:
(2x﹣3)2﹣(x+2y)(x﹣2y)﹣4y2,其中x=1,y=3.
【分析】直接利用乘法公式化简,再合并同类项,把已知代入即可.
解:原式=4x2﹣12x+9﹣(x2﹣4y2)﹣4y2
=4x2﹣12x+9﹣x2+4y2﹣4y2
=3x2﹣12x+9,
当x=1,y=3时,
原式=3﹣12+9=0.
20.(5分)已知:如图AB⊥BC于B,CD⊥BC于C,∠1=∠2.求证:BE∥CF.
证明:∵AB⊥BC,CD⊥BC(已知)
∴∠ABC=90°,∠BCD=90°( 垂直的定义 )
即∠1+∠3=90°,∠2+∠4=90°
又∵∠1=∠2( 已知 )
∴ ∠3 = ∠4 ( 等量代换 )
∴BE∥CF( 内错角相等,两直线平行 )
【分析】由垂直的定义得∠ABC=90°,∠BCD=90°,即∠1+∠3=90°,∠2+∠4=90°,求出∠3=∠4,即可得出结论.
解:,∵AB⊥BC,CD⊥BC(已知),
∴∠ABC=90°,∠BCD=90°(垂直的定义),
即∠1+∠3=90°,∠2+∠4=90°,
又∵∠1=∠2(已知),
∴∠3=∠4(等量代换),
∴BE∥CF(内错角相等,两直线平行).
故答案为:垂直的定义;已知;∠3,∠4,等量代换;内错角相等,两直线平行.
21.(6分)周老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000
米.一天,周老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.周老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)求a的值.
(2)b= 1100 ;c= 50 .
(3)求周老师从学校到家的平均速度.
【分析】(1)根据题意和题目中的数据,可以计算出a的值;
(2)根据题意,可以得到b的值,然后即可计算出c的值;
(3)根据题意可以得到周老师从学校到家用的总的时间,然后用总路程除以总时间,即可得到周老师从学校到家的平均速度.
解:(1)a=900÷45=20,
即a的值是20;
(2)由题意可得,
b=2000﹣900=1100,c=20+30=50,
故答案为:1100,50;
(3)周老师从学校到家用的总的时间为:50+1100÷110=50+10=60(分钟),
周老师从学校到家的平均速度是2000÷60=(米/分钟),
即周老师从学校到家的平均速度是米/分钟.
22.(8分)如图,在锐角三角形ABC中,CD、BE分别是AB、AC边上的高,且CD、BE交于一点P,若∠A=50°,求∠BPC的度数.
【分析】首先根据直角三角形的两个锐角互余,求得∠ABE的度数,再根据三角形的内角和定理的推论进行求解.
解:∵∠A=50°,BE⊥AC,
∴∠ABE=90°﹣50°=40°,
又∵CD⊥AB,
∴∠BPC=90°+∠ABE=130°.
23.(8分)如图,CF⊥AB于F,ED⊥AB于D,∠1=∠2,求证:FG∥BC.
【分析】根据平行线的判定推知DE∥FC;然后由平行线的性质、等量代换推知内错角∠3=∠2,则易证得结论.
【解答】证明:∵CF⊥AB,ED⊥AB,
∴DE∥FC,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴FG∥BC
24.(9分)把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
【分析】(1)此题根据面积的不同求解方法,可得到不同的表示方法.一种可以是3个正方形的面积和6个矩形的面积,另一种是直接利用正方形的面积公式计算,可得等式(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)利用(1)中的等式直接代入求得答案即可;
(3)利用S阴影=正方形ABCD的面积+正方形ECGF的面积﹣三角形BGF的面积﹣三角形ABD的面积求解.
解:(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2﹣2(ab+ac+bc)=121﹣76=45;
(3)∵a+b=10,ab=20,
∴S阴影=a2+b2﹣(a+b)?b﹣a2=a2+b2﹣ab=(a+b)2﹣ab=×102﹣×20=50﹣30=20.
25.(10分)已知直线l1∥l2,且l4和l1、l2分别交于A、B两点,点P为线段AB上的一个定点(如图1)
(1)写出∠1、∠2、∠3、之间的关系并说出理由.
(2)如果点P为线段AB上的动点时,问∠1、∠2、∠3之间的关系是否发生变化?(不必说理由)
(3)如果点P在A、B两点外侧运动时,(点P和点A、点B不重合)
①如图2,当点P在射线AB上运动时,∠1、∠2、∠3之间关系并说出理由.
②如图3,当点P在射线BA上运动时,∠1、∠2、∠3之间关系(不必说理由).
【分析】(1)延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;
(2)延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;
(3)画出图形,延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;
(4)画出图形,延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可.
解:
(1)延长DP交直线l2于E,如图1,
∵直线 l1∥l2,
∴∠DEC=∠1,
∵∠3=∠DEC+∠2,
∴∠3=∠2+∠1;
(2)不变化,∠3=∠1+∠2,
理由是:∵直线 l1∥l2,
∴∠DEC=∠1,
∴∠3=∠2+∠DEC=∠1+∠2,
(3)①当点P在射线AB上运动时,如图2,
∵直线 l1∥l2,
∴∠PFB=∠1,
∴∠PFB=∠2+∠3,
∴∠1=∠2+∠3,
②如图3,当点P在射线BA上运动时,
∵直线 l1∥l2,
∴∠PGA=∠2,
∴∠PGA=∠1+∠3,
∴∠2=∠1+∠3.
一、选择题(共8小题).
1.(3分)下列运算中,正确的是( )
A.a2+a3=a5 B.a6÷a3=a2 C.(a4)2=a6 D.a2?a3=a5
2.(3分)下列四个图形中,∠1和∠2是同位角的是( )
A. B.
C. D.
3.(3分)下列各式中,不能应用平方差公式进行计算的是( )
A.(﹣x+2y)(2y+x) B.(x+y)(x﹣y)
C.(a﹣b)(﹣a+b) D.(﹣2m+n)(﹣2m﹣n)
4.(3分)已知一个等腰三角形的两边长分别是2和5,那么这个等腰三角形的周长为( )
A.9 B.12 C.9或12 D.7
5.(3分)如图,下列推理不正确的是( )
A.∵AB∥CD,∴∠ABC+∠C=180° B.∵∠1=∠2,∴AD∥BC
C.∵AD∥BC,∴∠3=∠4 D.∵∠A+∠ADC=180°,∴AB∥CD
6.(3分)如图,表示某港口某日从6时到18时水深变化情况,每一艘轮船在水深不低于6米时可安全通航,满足这一要求的时间段是( )
A.12小时以后 B.14小时以后 C.10时到14时 D.12时到16时
7.(3分)下列说法正确的有( )
①等角的余角相等;②过一点有且只有一条直线与已知直线平行;③相等的角是对顶角;
④同位角相等;⑤过直线外一点做这条直线的垂线段,则这条垂线段叫做这个点到这条直线的距离.
A.1个 B.2个 C.3个 D.4个
8.(3分)我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(1)可以用来解释(a+b)2﹣(a﹣b)2=4ab.那么通过图(2)面积的计算,验证了一个恒等式,此等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.(a﹣b)(a+2b)=a2+ab﹣b2
二.填空题(本题满分24分,共8小题,每小题3分)
9.(3分)生物具有遗传多样性,遗传信息大多储存在DNA分子上,一个DNA分子的直径约为0.0000002cm.这个数量用科学记数法可表示为 cm.
10.(3分)计算32013×()2015的结果是 .
11.(3分)填空:x2﹣10x+ =( )2.
12.(3分)如图,直角三角形ABC中,AC⊥BC,CD⊥AB,点A到直线BC的距离等于线段 的长度,点A到直线CD的距离等于线段 的长度.
13.(3分)BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是 .
14.(3分)声音在空气中的传播速度v(m/s)与温度t(℃)的关系如表:
温度(℃) 0 5 10 15 20
速度v(m/s) 331 336 341 346 351
则速度v与温度t之间的关系式为 ;当t=30℃时,声音的传播速度为 m/s.
15.(3分)某人从A点出发向北偏东60°方向前进到达B点,再从B点出发向南偏西15°方向前进到达C点,则∠ABC= °.
16.(3分)观察下列各式:
13+23=9=×4×9=×22×32
13+23+33=36=×9×16=×32×42
13+23+33+43=100=×16×25=×42×52
若n为正整数,试猜想13+23+33+…+n3等于 .(注:最终结果保留带括号的形式即可)
三.作图题(本题满分4分)
17.(4分)用圆规、直尺作图,不写作法,但保留作图痕迹.
一木匠师傅打算在长方形木板上截一个平行四边形使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB,另一边过点C,且与AB平行,请帮忙确定这条边.
四.解答题
18.(16分)计算:
(1)﹣20+4﹣1×(﹣1)2008×()﹣2;
(2)(2x+1)(2x﹣1)﹣(2x+1)2;
(3)(a+3b﹣2c)(a﹣3b﹣2c);
(4)103×97(运用公式简算).
19.(6分)先化简,后求值:
(2x﹣3)2﹣(x+2y)(x﹣2y)﹣4y2,其中x=1,y=3.
20.(5分)已知:如图AB⊥BC于B,CD⊥BC于C,∠1=∠2.求证:BE∥CF.
证明:∵AB⊥BC,CD⊥BC(已知)
∴∠ABC=90°,∠BCD=90°( )
即∠1+∠3=90°,∠2+∠4=90°
又∵∠1=∠2( )
∴ = ( )
∴BE∥CF( )
21.(6分)周老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000
米.一天,周老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.周老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)求a的值.
(2)b= ;c= .
(3)求周老师从学校到家的平均速度.
22.(8分)如图,在锐角三角形ABC中,CD、BE分别是AB、AC边上的高,且CD、BE交于一点P,若∠A=50°,求∠BPC的度数.
23.(8分)如图,CF⊥AB于F,ED⊥AB于D,∠1=∠2,求证:FG∥BC.
24.(9分)把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
25.(10分)已知直线l1∥l2,且l4和l1、l2分别交于A、B两点,点P为线段AB上的一个定点(如图1)
(1)写出∠1、∠2、∠3、之间的关系并说出理由.
(2)如果点P为线段AB上的动点时,问∠1、∠2、∠3之间的关系是否发生变化?(不必说理由)
(3)如果点P在A、B两点外侧运动时,(点P和点A、点B不重合)
①如图2,当点P在射线AB上运动时,∠1、∠2、∠3之间关系并说出理由.
②如图3,当点P在射线BA上运动时,∠1、∠2、∠3之间关系(不必说理由).
参考答案
一.选择题(本题满分24分,共8小题,每小题3分)
1.(3分)下列运算中,正确的是( )
A.a2+a3=a5 B.a6÷a3=a2 C.(a4)2=a6 D.a2?a3=a5
【分析】根据合并同类项法则,同底数幂相除,底数不变指数相减;幂的乘方,底数不变指数相乘;同底数幂相乘,底数不变指数相加,对各选项分析判断后利用排除法求解.
解:A、a2与a3不是同类项,不能合并,故本选项错误;
B、a6÷a3=a3,故本选项错误;
C、(a4)2=a8,故本选项错误;
D、a2?a3=a5,故本选项正确.
故选:D.
2.(3分)下列四个图形中,∠1和∠2是同位角的是( )
A. B.
C. D.
【分析】同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角.
解:A图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角;
B图中,∠1与∠2的两边都不在同一条直线上,不是同位角;
C图中,∠1与∠2有一条边在同一条直线上,另一条边不在被截线的同一方,不是同位角;
D图中,∠1与∠2有一条边在同一条直线上,另一条边不在被截线的同一方,不是同位角.
故选:A.
3.(3分)下列各式中,不能应用平方差公式进行计算的是( )
A.(﹣x+2y)(2y+x) B.(x+y)(x﹣y)
C.(a﹣b)(﹣a+b) D.(﹣2m+n)(﹣2m﹣n)
【分析】利用平方差公式和完全平方公式对各选项进行判断.
解:(﹣x+2y)(2y+x)=(2y﹣x)(2y+x)=4y2﹣x2;
(x+y)(x﹣y)=x2﹣y2;
(a﹣b)(﹣a+b)=﹣(a﹣b)(a﹣b)=﹣(a﹣b)2=﹣a2+2ab+b2,
(﹣2m+n)(﹣2m﹣n)=(﹣2m)2﹣n2=4m2﹣n2.
故选:C.
4.(3分)已知一个等腰三角形的两边长分别是2和5,那么这个等腰三角形的周长为( )
A.9 B.12 C.9或12 D.7
【分析】题目给出等腰三角形有两条边长为2和5,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解:分两种情况:
当腰为2时,2+2<5,所以不能构成三角形;
当腰为5时,2+5>5,所以能构成三角形,周长是:2+5+5=12.
故选:B.
5.(3分)如图,下列推理不正确的是( )
A.∵AB∥CD,∴∠ABC+∠C=180° B.∵∠1=∠2,∴AD∥BC
C.∵AD∥BC,∴∠3=∠4 D.∵∠A+∠ADC=180°,∴AB∥CD
【分析】根据平行线的判定和性质逐项判断即可.
解:A、由AB∥CD,根据平行线的性质可得到∠ABC+∠BCD=180°,所以A正确;
B、由∠1=∠2可判定AD∥BC,所以B正确;
C、由AD∥BC,根据两直线平行,内错角相等可得到∠1=∠2,所以C不正确;
D、由∠A+∠ADC=180°,根据同旁内角互补两直线平行可得到AB∥CD,所以D正确;
故选:C.
6.(3分)如图,表示某港口某日从6时到18时水深变化情况,每一艘轮船在水深不低于6米时可安全通航,满足这一要求的时间段是( )
A.12小时以后 B.14小时以后 C.10时到14时 D.12时到16时
【分析】从图象上找到当水深为6米及6米以上的时间即可得到本题的答案.
解:∵当船底与水底间的距离不少于6米时,才能安全通过.
从图象可知水深为6米的时间为12时到16时,
故选:D.
7.(3分)下列说法正确的有( )
①等角的余角相等;②过一点有且只有一条直线与已知直线平行;③相等的角是对顶角;
④同位角相等;⑤过直线外一点做这条直线的垂线段,则这条垂线段叫做这个点到这条直线的距离.
A.1个 B.2个 C.3个 D.4个
【分析】根据平行线的性质、余角和补角的性质、点到直线的距离、对顶角的性质以及平行公理及推论即可判断.
解:①等角的余角相等,故此说法正确;
②过直线外一点有且只有一条直线与已知直线平行,故此说法错误;
③相等的角不一定是对顶角,故此说法错误;
④两直线平行,同位角相等,故此说法错误;
⑤过直线外一点做这条直线的垂线段,则这条垂线段叫做这个点到这条直线的距离,故此说法正确;
故选:B.
8.(3分)我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(1)可以用来解释(a+b)2﹣(a﹣b)2=4ab.那么通过图(2)面积的计算,验证了一个恒等式,此等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.(a﹣b)(a+2b)=a2+ab﹣b2
【分析】图(1)求的是阴影部分的面积,同样,图(2)正方形的面积用代数式表示即可.
解:图(2)中,
∵S空白正方形=a2﹣2b(a﹣b)﹣b2=a2﹣2ab+b2=(a﹣b)2,
∴(a﹣b)2=a2﹣2ab+b2.
故选:B.
二.填空题(本题满分24分,共8小题,每小题3分)
9.(3分)生物具有遗传多样性,遗传信息大多储存在DNA分子上,一个DNA分子的直径约为0.0000002cm.这个数量用科学记数法可表示为 2×10﹣7 cm.
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n.与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.在本题中a应为2,10的指数为﹣7.
解:0.000 000 2cm=2×10﹣7cm.
故答案为:2×10﹣7.
10.(3分)计算32013×()2015的结果是 .
【分析】根据积的乘方运算法则解答即可.
解:32013×()2015
=32013×()2013×
=×
=,
故答案为:.
11.(3分)填空:x2﹣10x+ 25 =( 5 )2.
【分析】根据完全平方公式解答即可.
解:x2﹣10x+()2=(x﹣)2,即x2﹣10x+25=(x﹣5)2,
故答案为:25;5.
12.(3分)如图,直角三角形ABC中,AC⊥BC,CD⊥AB,点A到直线BC的距离等于线段 AC 的长度,点A到直线CD的距离等于线段 AD 的长度.
【分析】利用点到直线的距离可得答案.
解:直角三角形ABC中,AC⊥BC,CD⊥AB,点A到直线BC的距离等于线段AC的长度,点A到直线CD的距离等于线段AD的长度.
故答案为:AC;AD.
13.(3分)BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是 2 .
【分析】根据三角形的中线的定义可得AD=CD,再求出△ABD和△BCD的周长的差=AB﹣BC.
解:∵BD是△ABC的中线,
∴AD=CD,
∴△ABD和△BCD的周长的差=(AB+BD+AD)﹣(BC+BD+CD)=AB﹣BC,
∵AB=5,BC=3,
∴△ABD和△BCD的周长的差=5﹣3=2.
故答案为:2.
14.(3分)声音在空气中的传播速度v(m/s)与温度t(℃)的关系如表:
温度(℃) 0 5 10 15 20
速度v(m/s) 331 336 341 346 351
则速度v与温度t之间的关系式为 v=t+331 ;当t=30℃时,声音的传播速度为 361 m/s.
【分析】根据表格中两个变量的变化规律,得出速度与温度之间变化的关系式,再代入求函数值即可.
解:根据表格中两个变量的变化规律可得,v=t+331;
当t=30时,v=30+331=361(m/s),
故答案为:v=t+331,361.
15.(3分)某人从A点出发向北偏东60°方向前进到达B点,再从B点出发向南偏西15°方向前进到达C点,则∠ABC= 45 °.
【分析】根据方向角的定义即可作出判断.
解:∠ABC=60°﹣15°=45°.
故答案是:45.
16.(3分)观察下列各式:
13+23=9=×4×9=×22×32
13+23+33=36=×9×16=×32×42
13+23+33+43=100=×16×25=×42×52
若n为正整数,试猜想13+23+33+…+n3等于 n2(n+1)2 .(注:最终结果保留带括号的形式即可)
【分析】由所给的数据,得出变化规律,即是乘以最后一个数的平方,再乘以最后一个数加1的平方,即可得出答案.
解:根据题意得,13+23+33+4+…+n3=n2(n+1)2.
故答案为n2(n+1)2.
三.作图题(本题满分4分)
17.(4分)用圆规、直尺作图,不写作法,但保留作图痕迹.
一木匠师傅打算在长方形木板上截一个平行四边形使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB,另一边过点C,且与AB平行,请帮忙确定这条边.
【分析】在射线BE上截取DB,使得BD=AC,作直线CD即可,四边形ABDC即为所求.
解:如图,平行四边形ABDC即为所求.
四.解答题
18.(16分)计算:
(1)﹣20+4﹣1×(﹣1)2008×()﹣2;
(2)(2x+1)(2x﹣1)﹣(2x+1)2;
(3)(a+3b﹣2c)(a﹣3b﹣2c);
(4)103×97(运用公式简算).
【分析】(1)根据零指数幂、负整数指数幂、有理数的乘方的运算法则进行计算即可;
(2)用平方差公式和完全平方公式将式子展开后进行合并即可;
(3)可用平方差公式和完全平方公式进行计算即可;
(4)利用平方差公式计算即可.
解:(1)原式=﹣1+0.25×1×4
=﹣1+1
=0;
(2)原式=4x2﹣1﹣(4x2+4x+1)
=4x2﹣1﹣4x2﹣4x﹣1
=﹣4x﹣2;
(3)原式=(a﹣2c)2﹣9b2
=a2﹣4ac+4c2﹣9b2;
(4)原式=(100+3)×(100﹣3)
=1002﹣32
=10000﹣9
=9991.
19.(6分)先化简,后求值:
(2x﹣3)2﹣(x+2y)(x﹣2y)﹣4y2,其中x=1,y=3.
【分析】直接利用乘法公式化简,再合并同类项,把已知代入即可.
解:原式=4x2﹣12x+9﹣(x2﹣4y2)﹣4y2
=4x2﹣12x+9﹣x2+4y2﹣4y2
=3x2﹣12x+9,
当x=1,y=3时,
原式=3﹣12+9=0.
20.(5分)已知:如图AB⊥BC于B,CD⊥BC于C,∠1=∠2.求证:BE∥CF.
证明:∵AB⊥BC,CD⊥BC(已知)
∴∠ABC=90°,∠BCD=90°( 垂直的定义 )
即∠1+∠3=90°,∠2+∠4=90°
又∵∠1=∠2( 已知 )
∴ ∠3 = ∠4 ( 等量代换 )
∴BE∥CF( 内错角相等,两直线平行 )
【分析】由垂直的定义得∠ABC=90°,∠BCD=90°,即∠1+∠3=90°,∠2+∠4=90°,求出∠3=∠4,即可得出结论.
解:,∵AB⊥BC,CD⊥BC(已知),
∴∠ABC=90°,∠BCD=90°(垂直的定义),
即∠1+∠3=90°,∠2+∠4=90°,
又∵∠1=∠2(已知),
∴∠3=∠4(等量代换),
∴BE∥CF(内错角相等,两直线平行).
故答案为:垂直的定义;已知;∠3,∠4,等量代换;内错角相等,两直线平行.
21.(6分)周老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000
米.一天,周老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.周老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)求a的值.
(2)b= 1100 ;c= 50 .
(3)求周老师从学校到家的平均速度.
【分析】(1)根据题意和题目中的数据,可以计算出a的值;
(2)根据题意,可以得到b的值,然后即可计算出c的值;
(3)根据题意可以得到周老师从学校到家用的总的时间,然后用总路程除以总时间,即可得到周老师从学校到家的平均速度.
解:(1)a=900÷45=20,
即a的值是20;
(2)由题意可得,
b=2000﹣900=1100,c=20+30=50,
故答案为:1100,50;
(3)周老师从学校到家用的总的时间为:50+1100÷110=50+10=60(分钟),
周老师从学校到家的平均速度是2000÷60=(米/分钟),
即周老师从学校到家的平均速度是米/分钟.
22.(8分)如图,在锐角三角形ABC中,CD、BE分别是AB、AC边上的高,且CD、BE交于一点P,若∠A=50°,求∠BPC的度数.
【分析】首先根据直角三角形的两个锐角互余,求得∠ABE的度数,再根据三角形的内角和定理的推论进行求解.
解:∵∠A=50°,BE⊥AC,
∴∠ABE=90°﹣50°=40°,
又∵CD⊥AB,
∴∠BPC=90°+∠ABE=130°.
23.(8分)如图,CF⊥AB于F,ED⊥AB于D,∠1=∠2,求证:FG∥BC.
【分析】根据平行线的判定推知DE∥FC;然后由平行线的性质、等量代换推知内错角∠3=∠2,则易证得结论.
【解答】证明:∵CF⊥AB,ED⊥AB,
∴DE∥FC,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴FG∥BC
24.(9分)把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
【分析】(1)此题根据面积的不同求解方法,可得到不同的表示方法.一种可以是3个正方形的面积和6个矩形的面积,另一种是直接利用正方形的面积公式计算,可得等式(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)利用(1)中的等式直接代入求得答案即可;
(3)利用S阴影=正方形ABCD的面积+正方形ECGF的面积﹣三角形BGF的面积﹣三角形ABD的面积求解.
解:(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2﹣2(ab+ac+bc)=121﹣76=45;
(3)∵a+b=10,ab=20,
∴S阴影=a2+b2﹣(a+b)?b﹣a2=a2+b2﹣ab=(a+b)2﹣ab=×102﹣×20=50﹣30=20.
25.(10分)已知直线l1∥l2,且l4和l1、l2分别交于A、B两点,点P为线段AB上的一个定点(如图1)
(1)写出∠1、∠2、∠3、之间的关系并说出理由.
(2)如果点P为线段AB上的动点时,问∠1、∠2、∠3之间的关系是否发生变化?(不必说理由)
(3)如果点P在A、B两点外侧运动时,(点P和点A、点B不重合)
①如图2,当点P在射线AB上运动时,∠1、∠2、∠3之间关系并说出理由.
②如图3,当点P在射线BA上运动时,∠1、∠2、∠3之间关系(不必说理由).
【分析】(1)延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;
(2)延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;
(3)画出图形,延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;
(4)画出图形,延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可.
解:
(1)延长DP交直线l2于E,如图1,
∵直线 l1∥l2,
∴∠DEC=∠1,
∵∠3=∠DEC+∠2,
∴∠3=∠2+∠1;
(2)不变化,∠3=∠1+∠2,
理由是:∵直线 l1∥l2,
∴∠DEC=∠1,
∴∠3=∠2+∠DEC=∠1+∠2,
(3)①当点P在射线AB上运动时,如图2,
∵直线 l1∥l2,
∴∠PFB=∠1,
∴∠PFB=∠2+∠3,
∴∠1=∠2+∠3,
②如图3,当点P在射线BA上运动时,
∵直线 l1∥l2,
∴∠PGA=∠2,
∴∠PGA=∠1+∠3,
∴∠2=∠1+∠3.
同课章节目录
