2019-2020学年山东省菏泽市牡丹区七年级下学期期末数学试卷 (word版,含解析)
文档属性
| 名称 | 2019-2020学年山东省菏泽市牡丹区七年级下学期期末数学试卷 (word版,含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 638.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
图片预览




文档简介
2019-2020学年山东省菏泽市牡丹区七年级第二学期期末数学试卷
一、选择题(共10小题).
1.(3分)在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是( )
A. B. C. D.
2.(3分)下列运算正确的是( )
A.3a+2a=5a2 B.(2a)3=6a3
C.(x+1)2=x2+1 D.(x+2)(x﹣2)=x2﹣4
3.(3分)有人预测2020年东京奥运会上中国女排夺冠的概率是80%,对这个说法正确的理解应该是( )
A.中国女排一定会夺冠
B.中国女排一定不会夺冠
C.中国女排夺冠的可能性比较大
D.中国女排夺冠的可能性比较小
4.(3分)2019新型冠状病毒(2019﹣nCoV),2020年1月12日被世命名,科学家借助比光学显微镜更加厉害的电子显微镜发现新型冠状病毒的大小约为0.000000125米.则数据0.000000125用科学记数法表示正确的是( )
A.1.25×107 B.1.25×10﹣7 C.1.25×108 D.1.25×10﹣8
5.(3分)下列说法错误的是( )
A.关于某条直线对称的两个三角形一定全等
B.到线段两端点距离相等的点有无数个
C.等腰三角形的中线、高、角平分线三线合一
D.轴对称图形的对称轴是对称点所连线段的垂直平分线
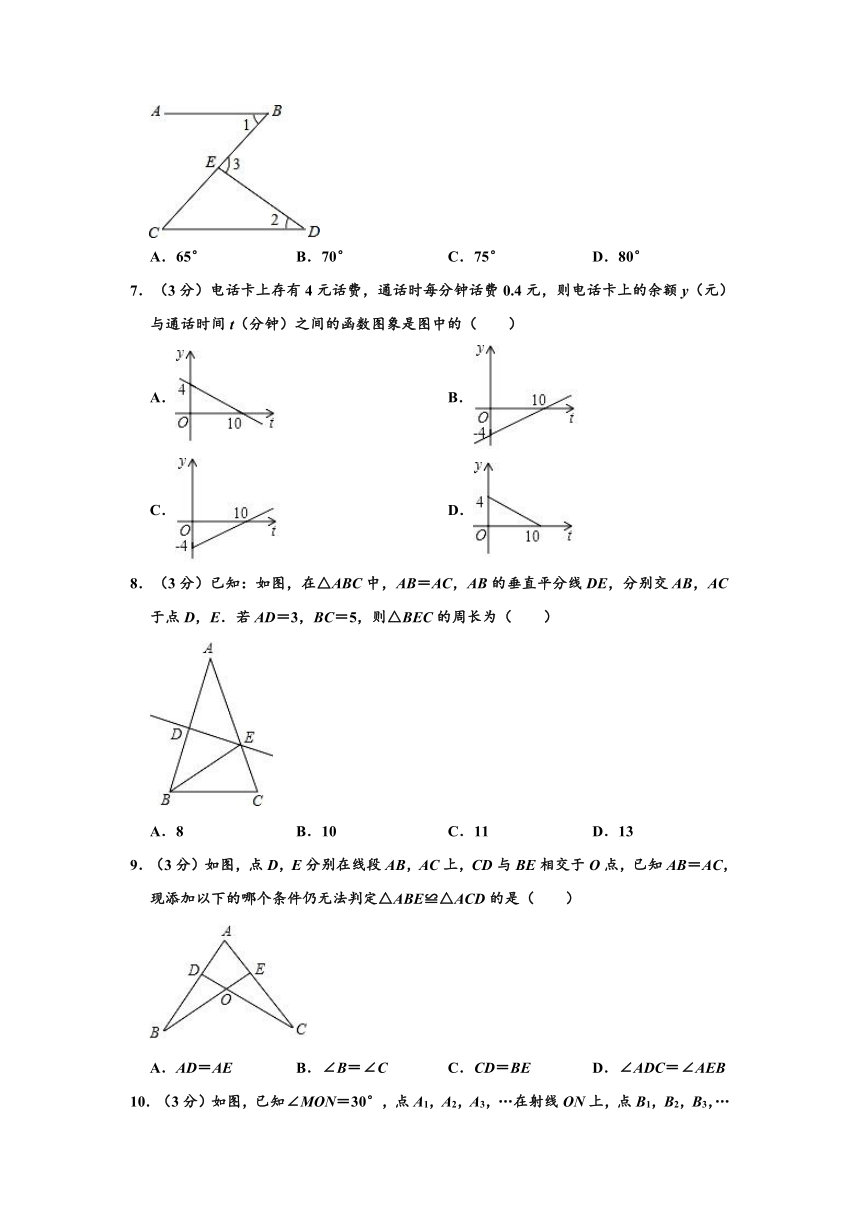
6.(3分)如图,已知AB∥CD,直线AB,CD被BC所截,E点在BC上,若∠1=45°,∠2=35°,则∠3=( )
A.65° B.70° C.75° D.80°
7.(3分)电话卡上存有4元话费,通话时每分钟话费0.4元,则电话卡上的余额y(元)与通话时间t(分钟)之间的函数图象是图中的( )
A. B.
C. D.
8.(3分)已知:如图,在△ABC中,AB=AC,AB的垂直平分线DE,分别交AB,AC于点D,E.若AD=3,BC=5,则△BEC的周长为( )
A.8 B.10 C.11 D.13
9.(3分)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
10.(3分)如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1B2,△A2B2B3,△A3B3B4,…均为等边三角形.若OB1=1,则△A8B8B9的边长为( )
A.64 B.128 C.132 D.256
二.填空题(每小题3分,共24分)
11.(3分)计算:x(x﹣1)= .
12.(3分)若x+m与2﹣x的乘积中不含x的一次项,则实数m的值为 .
13.(3分)如果等腰三角形的一个角是70°,那么它的顶角是 度.
14.(3分)如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,BC=8cm,则DE+DB= .
15.(3分)一辆汽车油箱中现存油50L,汽车每行驶100km耗油10L,则油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是 .
16.(3分)将一张长方形纸条折成如图所示的图形,如果∠1=64°,那么∠2= .
17.(3分)如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C= 度.
18.(3分)如图1,在长方形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P的运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则长方形ABCD的周长是 .
三.解答题(共46分)
19.(9分)(1)计算:(﹣1)﹣3+(2019﹣π)0﹣|﹣5|;
(2)先化简,再求值:[(x﹣2y)2﹣(3y+x)(x﹣3y)+3y2]÷4y,其中x=2,y=1.
20.(6分)已知:如图,AE平分∠BAC,CE平分∠ACD,且∠a+∠β=90°.
求证:AB∥CD.
21.(8分)如图描述了一辆汽车在某一直路上的行驶过程,汽车离出发地的距离s(km)和行驶时间t(h)之间的关系,请根据图象回答下列问题:
(1)汽车共行驶的路程是多少?
(2)汽车在行驶途中停留了多长时间?
(3)汽车在每个行驶过程中的速度分别是多少?
(4)汽车到达离出发地最远的地方后返回,则返回用了多长时间?
22.(8分)如图,在四边形ABCD中,AB=BC,BF平分∠ABC,AF∥DC,连接AC,CF.
求证:(1)AF=CF;(2)CA平分∠DCF.
23.(6分)甲、乙两人玩赢卡片游戏,工具是一个如图所示的转盘(等分成8份),游戏规定:自由转动的转盘,当转盘停止后指针指向字母“A”,则甲输给乙2张卡片,若指针指向字母“B”,则乙输给甲3张卡片;若指针指向字母“C”,则乙输给甲1张卡片(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止).
(1)转动一次转盘,求甲赢取1张卡片的概率;
(2)转动一次转盘,求乙赢取2张卡片的概率;
(3)转动一次转盘,求甲赢取卡片的概率.
24.(9分)如图,点D在射线BC上运动,△ABC与△ADE都是以点A为直角顶点的等腰直角三角形.
(1)在图1中找出一对全等三角形并说明理由;
(2)试在图1中说明EC⊥BC;
(3)如图2,当点D在BC的延长线上时,若BC=6,BD=x(x>6),△CDE的面积为y,试求出y与x之间的关系式.
参考答案
一.选择题(请把正确答案填涂在答题卡上,每小题3分,共30分)
1.(3分)在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是( )
A. B. C. D.
【分析】根据轴对称图形的概念求解.
解:A、不是轴对称图形,故此选项不合题意;
B、不是轴对称图形,故此选项不合题意;
C、是轴对称图形,故此选项符合题意;
D、不是轴对称图形,故此选项不合题意.
故选:C.
2.(3分)下列运算正确的是( )
A.3a+2a=5a2 B.(2a)3=6a3
C.(x+1)2=x2+1 D.(x+2)(x﹣2)=x2﹣4
【分析】分别利用合并同类项法则以及积的乘方运算法则和完全平方公式以及平方差公式分别计算得出答案.
解:A、3a+2a=5a,故此选项错误;
B、(2a)3=8a3,故此选项错误;
C、(x+1)2=x2+2x+1,故此选项错误;
D、(x+2)(x﹣2)=x2﹣4,正确.
故选:D.
3.(3分)有人预测2020年东京奥运会上中国女排夺冠的概率是80%,对这个说法正确的理解应该是( )
A.中国女排一定会夺冠
B.中国女排一定不会夺冠
C.中国女排夺冠的可能性比较大
D.中国女排夺冠的可能性比较小
【分析】直接利用概率的意义得出答案.
解:有人预测2020年东京奥运会上中国女排夺冠的概率是80%,对这个说法正确的理解应该:中国女排夺冠的可能性比较大.
故选:C.
4.(3分)2019新型冠状病毒(2019﹣nCoV),2020年1月12日被世命名,科学家借助比光学显微镜更加厉害的电子显微镜发现新型冠状病毒的大小约为0.000000125米.则数据0.000000125用科学记数法表示正确的是( )
A.1.25×107 B.1.25×10﹣7 C.1.25×108 D.1.25×10﹣8
【分析】绝对值小于1的负数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.000000125=1.25×10﹣7.
故选:B.
5.(3分)下列说法错误的是( )
A.关于某条直线对称的两个三角形一定全等
B.到线段两端点距离相等的点有无数个
C.等腰三角形的中线、高、角平分线三线合一
D.轴对称图形的对称轴是对称点所连线段的垂直平分线
【分析】根据关于某条直线对称的图形叫轴对称图形,以及等腰三角形的性质分别判断得出答案.
解:A、关于某条直线对称的两个三角形一定全等,正确,不合题意;
B、到线段两端点距离相等的点有无数个,正确,不合题意;
C、等腰三角形底边上的中线、高、角平分线三线合一,故原说法错误,符合题意;
D、轴对称图形的对称轴是对称点所连线段的垂直平分线,正确,不合题意;
故选:C.
6.(3分)如图,已知AB∥CD,直线AB,CD被BC所截,E点在BC上,若∠1=45°,∠2=35°,则∠3=( )
A.65° B.70° C.75° D.80°
【分析】由平行线的性质可求得∠C,在△CDE中利用三角形外的性质可求得∠3.
解:
∵AB∥CD,
∴∠C=∠1=45°,
∵∠3是△CDE的一个外角,
∴∠3=∠C+∠2=45°+35°=80°,
故选:D.
7.(3分)电话卡上存有4元话费,通话时每分钟话费0.4元,则电话卡上的余额y(元)与通话时间t(分钟)之间的函数图象是图中的( )
A. B.
C. D.
【分析】根据当通话时间为0时,余额为4元;当通话时间为10时,余额为0元.据此判断即可.
解:由题意可知:当通话时间为0时,余额为4元;当通话时间为10时,余额为0元.
∴y=4﹣0.4t(0≤t≤10),
故只有选项D符合题意.
故选:D.
8.(3分)已知:如图,在△ABC中,AB=AC,AB的垂直平分线DE,分别交AB,AC于点D,E.若AD=3,BC=5,则△BEC的周长为( )
A.8 B.10 C.11 D.13
【分析】由AB的垂直平分线DE分别交AB、AC于点D、E,易得△EBC的周长=AC+BC;
解:∵AB的垂直平分线DE分别交AB、AC于点D、E,
∴AE=BE,
∵AD=3,
∴AB=6,
∴AE+EC=AC=AB=6,
∵BC=5,
∴△EBC的周长=BC+BE+CE=BC+AE+CE=BC+AC=6+5=11;
故选:C.
9.(3分)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
【分析】根据全等三角形的判定方法对各选项进行判断.
解:∵AB=AC,∠BAE=∠CAD,
∴当添加AE=AD时,可根据“SAS”判断△ABE≌△ACD;
当添加∠B=∠C时,可根据“ASA”判断△ABE≌△ACD;
当添加∠AEB=∠ADC时,可根据“AAS”判断△ABE≌△ACD.
故选:C.
10.(3分)如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1B2,△A2B2B3,△A3B3B4,…均为等边三角形.若OB1=1,则△A8B8B9的边长为( )
A.64 B.128 C.132 D.256
【分析】根据等腰三角形的性质以及平行线的性质得出B1A1∥A2B2∥A3B3,以及a2=2a1,得出a3=4a1=4,a4=8a1=8,a5=16a1…进而得出答案.
解:∵△A1B1B2是等边三角形,
∴∠A1B1B2=∠A1B2O=60°,A1B1=A1B2,
∵∠O=30°,
∴∠A2A1B2=∠O+∠A1B2O=90°,
∵∠A1B1B2=∠O+∠OA1B1,
∴∠O=∠OA1B1=30°,
∴OB1=A1B1=A1B2=1,
在Rt△A2A1B2中,∵∠A1A2B2=30°
∴A2B2=2A1B2=2,
同法可得A3B3=22,A4B4=23,…,AnBn=2n﹣1,
∴△A8B8B9的边长=27=128,
故选:B.
二.填空题(每小题3分,共24分)
11.(3分)计算:x(x﹣1)= x2﹣x .
【分析】根据单项式乘多项式法则计算可得.
解:x(x﹣1)=x2﹣x,
故答案为:x2﹣x.
12.(3分)若x+m与2﹣x的乘积中不含x的一次项,则实数m的值为 2 .
【分析】根据多项式乘以多项式的法则,可表示为(a+b)(m+n)=am+an+bm+bn,计算即可.
解:根据题意得:
(x+m)(2﹣x)=2x﹣x2+2m﹣mx,
∵x+m与2﹣x的乘积中不含x的一次项,
∴m=2;
故答案为:2.
13.(3分)如果等腰三角形的一个角是70°,那么它的顶角是 70或40 度.
【分析】由于题中没有明确说明70°是顶角还是底角,故分两种情况考虑:当70°是顶角,显然得到结果;当70°是底角时,根据等腰三角形的性质得到两底角都为70°,利用三角形的内角和定理即可求出此时的顶角.
解:若70°为顶角,则此等腰三角形的顶角是70°;
若70°为底角,则此等腰三角形的顶角为180°﹣2×70°=40°,
综上,此等腰三角形的顶角为70°或40°.
故答案为:70或40
14.(3分)如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,BC=8cm,则DE+DB= 8cm .
【分析】根据角平分线性质得出DE=CD,求出BD+DE=BC,即可得出答案.
解:∵在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,
∴DC=DE,
∵BC=8cm,
∴DE+BD=CD+BD=BC=8cm,
故答案为:8cm.
15.(3分)一辆汽车油箱中现存油50L,汽车每行驶100km耗油10L,则油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是 y=﹣0.1x+50 .
【分析】由于汽车每行驶100km耗油10L,那么汽车行驶路程x千米耗油0.1xL,而汽车油箱中能盛汽油50L,由此即可确定加满油后,油箱中剩余油量y(L)与汽车行驶路程x(km)之间的函数关系式.
解:∵汽车每行驶100km耗油10L,
∴汽车行驶路程xkm耗油0.1xL,
∵汽车油箱中现存油50L,
∴油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是y=﹣0.1x+50.
故答案是:y=﹣0.1x+50.
16.(3分)将一张长方形纸条折成如图所示的图形,如果∠1=64°,那么∠2= 58° .
【分析】由折叠可得,∠2=∠CEF,再根据平角的定义,即可得到∠2的度数.
解:由折叠可得,∠2=∠CEF,
∵∠1=64°,
∴∠2=(180°﹣64°)=58°,
故答案为:58°.
17.(3分)如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C= 24 度.
【分析】根据线段的垂直平分线的性质得到EA=EC,得到∠EAC=∠C,根据角平分线的定义、三角形内角和定理计算即可.
解:∵DE是AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C,
∴∠FAC=∠EAC+19°,
∵AF平分∠BAC,
∴∠FAB=∠EAC+19°,
∵∠B+∠BAC+∠C=180°,
∴70°+2(∠C+19°)+∠C=180°,
解得,∠C=24°,
故答案为:24.
18.(3分)如图1,在长方形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P的运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则长方形ABCD的周长是 16 .
【分析】根据函数的图象、结合图形求出AB、BC的值,根据长方形的周长公式得出长方形ABCD的周长.
解:∵动点P从点B出发,沿BC、CD、DA运动至点A停止,而当点P运动到点C,D之间时,△ABP的面积不变,
函数图象上横轴表示点P运动的路程,x=4时,y开始不变,说明BC=3,x=8时,接着变化,说明CD=8﹣3=5,
∴AB=5,BC=3,
长方形ABCD的周长是:2(AB+BC)=16,
故答案为:16
三.解答题(共46分)
19.(9分)(1)计算:(﹣1)﹣3+(2019﹣π)0﹣|﹣5|;
(2)先化简,再求值:[(x﹣2y)2﹣(3y+x)(x﹣3y)+3y2]÷4y,其中x=2,y=1.
【分析】(1)先根据负整数指数幂,零指数幂,绝对值进行计算,再求出即可;
(2)先算括号内的乘法,再合并同类项,算除法,最后代入求出即可.
解:(1)(﹣1)﹣3+(2019﹣π)0﹣|﹣5|
=﹣1+1﹣5
=﹣5;
(2)[(x﹣2y)2﹣(3y+x)(x﹣3y)+3y2]÷4y
=(x2﹣4xy+4y2﹣x2+9y2+3y2)÷4y
=(16y2 ﹣4xy)÷4y
=4y﹣x,
当x=2,y=1时,原式=4×1﹣2=2.
20.(6分)已知:如图,AE平分∠BAC,CE平分∠ACD,且∠a+∠β=90°.
求证:AB∥CD.
【分析】根据角平分线的定义和平行线的判定定理即可得到结论.
【解答】证明:∵CE平分∠ACD,
∴∠ACD=2∠α.
∵AE平分∠BAC,
∴∠BAC=2∠β,
∴∠ACD+∠BAC=2∠α+2∠β.
即∠ACD+∠BAC=2(∠α+∠β).
∵∠α+∠β=90°,
∴∠ACD+∠BAC=180°,
∴AB∥CD.
21.(8分)如图描述了一辆汽车在某一直路上的行驶过程,汽车离出发地的距离s(km)和行驶时间t(h)之间的关系,请根据图象回答下列问题:
(1)汽车共行驶的路程是多少?
(2)汽车在行驶途中停留了多长时间?
(3)汽车在每个行驶过程中的速度分别是多少?
(4)汽车到达离出发地最远的地方后返回,则返回用了多长时间?
【分析】(1)观察函数图象的纵坐标,可得汽车行驶的路程;
(2)观察函数图象,可得平行于t轴的线段;
(3)分四种情形分别求解.
(4)观察函数图象的横坐标,可得到达最远地方的时间,回到出发点的时间,根据有理数的减法,可得答案.
解:(1)由纵坐标看出汽车最远行驶路程是120千米,往返共行驶的路程是120×2=240千米;
(2)由横坐标看出,2﹣1.5=0.5,汽车在行驶途中停留了0.5小时;
(3)线段AB上的速度为:千米/小时,线段BC上的速度为0,线段CD上的速度为40千米/小时,线段DE上的速度为:80千米/小时.
(4)由横坐标看出4.5﹣3=1.5,返回用了1.5小时.
22.(8分)如图,在四边形ABCD中,AB=BC,BF平分∠ABC,AF∥DC,连接AC,CF.
求证:(1)AF=CF;(2)CA平分∠DCF.
【分析】(1)根据BF平分∠ABC?∠ABF=∠CBF,再加上AB=BC,BF=BF就可以推出△ABF≌△CBF,依据全等三角形对应边相等的性质可以推出AF=CF;
(2)根据(1)中所得出的结论可以推出∠FCA=∠FAC;依据平行线的性质可以得出内错角∠FAC、∠DCA相等,等量代换后,就可推出CA平分∠DCF.
【解答】证明:如图.
(1)∵BF平分∠ABC,
∴∠ABF=∠CBF.(1分)
在△ABF与△CBF中,
∴△ABF≌△CBF(SAS).(2分)
∴AF=CF.(3分)
(2)∵AF=CF,
∴∠FCA=∠FAC.(4分)
∵AF∥DC,
∴∠FAC=∠DCA.
∴∠FCA=∠DCA,即CA平分∠DCF.(5分)
23.(6分)甲、乙两人玩赢卡片游戏,工具是一个如图所示的转盘(等分成8份),游戏规定:自由转动的转盘,当转盘停止后指针指向字母“A”,则甲输给乙2张卡片,若指针指向字母“B”,则乙输给甲3张卡片;若指针指向字母“C”,则乙输给甲1张卡片(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止).
(1)转动一次转盘,求甲赢取1张卡片的概率;
(2)转动一次转盘,求乙赢取2张卡片的概率;
(3)转动一次转盘,求甲赢取卡片的概率.
【分析】根据已知条件得出共有8种等可能的结果,甲赢取卡片有4种结果,乙赢取卡2张片有4种结果,甲赢取卡1张片有3种结果,再根据概率公式即可求出(1)(2)(3).
解:共有8种等可能的结果,甲赢取卡片有4种结果,乙赢取卡2张片有4种结果,甲赢取卡1张片有3种结果,
(1)甲赢取1张卡片的概率是:P(甲赢取1张卡片)=;
(2)乙赢取2张卡片的概率是:P(乙赢取2张卡片)==;
(3)甲赢取卡片的概率是:P(甲赢取卡片)==;
24.(9分)如图,点D在射线BC上运动,△ABC与△ADE都是以点A为直角顶点的等腰直角三角形.
(1)在图1中找出一对全等三角形并说明理由;
(2)试在图1中说明EC⊥BC;
(3)如图2,当点D在BC的延长线上时,若BC=6,BD=x(x>6),△CDE的面积为y,试求出y与x之间的关系式.
【分析】(1)根据等腰直角三角形的性质得到∠BAC=90°,∠DAE=90°,AB=AC,AD=AE,利用SAS定理证明△ABD≌△ACE;
(2)根据等腰直角三角形的性质、全等三角形的性质解答;
(3)证明△ABD≌△ACE,根据全等三角形的性质得到BD=EC,∠ACE=∠B=45°,根据三角形的面积公式计算,求出y与x之间的关系式.
解:(1)△ABD≌△ACE.
理由如下:∵△ABC与△ADE都是以点A为直角顶点的等腰直角三角形,
∴∠BAC=90°,∠DAE=90°,AB=AC,AD=AE,
∴∠BAD+∠DAC=∠CAE+∠DAC=90°,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS);
(2)证明:∵△ABD≌△ACE,
∴∠ACE=∠B=45°.
∵∠ACB=45°,
∴∠ECD=90°,
∴EC⊥BC;
(3)解:∵∠BAD+∠DAC=∠CAE+∠DAC=90°,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=EC,∠ACE=∠B=45°,
∵∠ACB=45°,
∴∠ECD=90°,
∴EC⊥BC,
∴S△ECD=CD?EC,
∴y=(x﹣6)?x=x2﹣3x(x>6).
一、选择题(共10小题).
1.(3分)在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是( )
A. B. C. D.
2.(3分)下列运算正确的是( )
A.3a+2a=5a2 B.(2a)3=6a3
C.(x+1)2=x2+1 D.(x+2)(x﹣2)=x2﹣4
3.(3分)有人预测2020年东京奥运会上中国女排夺冠的概率是80%,对这个说法正确的理解应该是( )
A.中国女排一定会夺冠
B.中国女排一定不会夺冠
C.中国女排夺冠的可能性比较大
D.中国女排夺冠的可能性比较小
4.(3分)2019新型冠状病毒(2019﹣nCoV),2020年1月12日被世命名,科学家借助比光学显微镜更加厉害的电子显微镜发现新型冠状病毒的大小约为0.000000125米.则数据0.000000125用科学记数法表示正确的是( )
A.1.25×107 B.1.25×10﹣7 C.1.25×108 D.1.25×10﹣8
5.(3分)下列说法错误的是( )
A.关于某条直线对称的两个三角形一定全等
B.到线段两端点距离相等的点有无数个
C.等腰三角形的中线、高、角平分线三线合一
D.轴对称图形的对称轴是对称点所连线段的垂直平分线
6.(3分)如图,已知AB∥CD,直线AB,CD被BC所截,E点在BC上,若∠1=45°,∠2=35°,则∠3=( )
A.65° B.70° C.75° D.80°
7.(3分)电话卡上存有4元话费,通话时每分钟话费0.4元,则电话卡上的余额y(元)与通话时间t(分钟)之间的函数图象是图中的( )
A. B.
C. D.
8.(3分)已知:如图,在△ABC中,AB=AC,AB的垂直平分线DE,分别交AB,AC于点D,E.若AD=3,BC=5,则△BEC的周长为( )
A.8 B.10 C.11 D.13
9.(3分)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
10.(3分)如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1B2,△A2B2B3,△A3B3B4,…均为等边三角形.若OB1=1,则△A8B8B9的边长为( )
A.64 B.128 C.132 D.256
二.填空题(每小题3分,共24分)
11.(3分)计算:x(x﹣1)= .
12.(3分)若x+m与2﹣x的乘积中不含x的一次项,则实数m的值为 .
13.(3分)如果等腰三角形的一个角是70°,那么它的顶角是 度.
14.(3分)如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,BC=8cm,则DE+DB= .
15.(3分)一辆汽车油箱中现存油50L,汽车每行驶100km耗油10L,则油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是 .
16.(3分)将一张长方形纸条折成如图所示的图形,如果∠1=64°,那么∠2= .
17.(3分)如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C= 度.
18.(3分)如图1,在长方形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P的运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则长方形ABCD的周长是 .
三.解答题(共46分)
19.(9分)(1)计算:(﹣1)﹣3+(2019﹣π)0﹣|﹣5|;
(2)先化简,再求值:[(x﹣2y)2﹣(3y+x)(x﹣3y)+3y2]÷4y,其中x=2,y=1.
20.(6分)已知:如图,AE平分∠BAC,CE平分∠ACD,且∠a+∠β=90°.
求证:AB∥CD.
21.(8分)如图描述了一辆汽车在某一直路上的行驶过程,汽车离出发地的距离s(km)和行驶时间t(h)之间的关系,请根据图象回答下列问题:
(1)汽车共行驶的路程是多少?
(2)汽车在行驶途中停留了多长时间?
(3)汽车在每个行驶过程中的速度分别是多少?
(4)汽车到达离出发地最远的地方后返回,则返回用了多长时间?
22.(8分)如图,在四边形ABCD中,AB=BC,BF平分∠ABC,AF∥DC,连接AC,CF.
求证:(1)AF=CF;(2)CA平分∠DCF.
23.(6分)甲、乙两人玩赢卡片游戏,工具是一个如图所示的转盘(等分成8份),游戏规定:自由转动的转盘,当转盘停止后指针指向字母“A”,则甲输给乙2张卡片,若指针指向字母“B”,则乙输给甲3张卡片;若指针指向字母“C”,则乙输给甲1张卡片(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止).
(1)转动一次转盘,求甲赢取1张卡片的概率;
(2)转动一次转盘,求乙赢取2张卡片的概率;
(3)转动一次转盘,求甲赢取卡片的概率.
24.(9分)如图,点D在射线BC上运动,△ABC与△ADE都是以点A为直角顶点的等腰直角三角形.
(1)在图1中找出一对全等三角形并说明理由;
(2)试在图1中说明EC⊥BC;
(3)如图2,当点D在BC的延长线上时,若BC=6,BD=x(x>6),△CDE的面积为y,试求出y与x之间的关系式.
参考答案
一.选择题(请把正确答案填涂在答题卡上,每小题3分,共30分)
1.(3分)在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中.轴对称图形是( )
A. B. C. D.
【分析】根据轴对称图形的概念求解.
解:A、不是轴对称图形,故此选项不合题意;
B、不是轴对称图形,故此选项不合题意;
C、是轴对称图形,故此选项符合题意;
D、不是轴对称图形,故此选项不合题意.
故选:C.
2.(3分)下列运算正确的是( )
A.3a+2a=5a2 B.(2a)3=6a3
C.(x+1)2=x2+1 D.(x+2)(x﹣2)=x2﹣4
【分析】分别利用合并同类项法则以及积的乘方运算法则和完全平方公式以及平方差公式分别计算得出答案.
解:A、3a+2a=5a,故此选项错误;
B、(2a)3=8a3,故此选项错误;
C、(x+1)2=x2+2x+1,故此选项错误;
D、(x+2)(x﹣2)=x2﹣4,正确.
故选:D.
3.(3分)有人预测2020年东京奥运会上中国女排夺冠的概率是80%,对这个说法正确的理解应该是( )
A.中国女排一定会夺冠
B.中国女排一定不会夺冠
C.中国女排夺冠的可能性比较大
D.中国女排夺冠的可能性比较小
【分析】直接利用概率的意义得出答案.
解:有人预测2020年东京奥运会上中国女排夺冠的概率是80%,对这个说法正确的理解应该:中国女排夺冠的可能性比较大.
故选:C.
4.(3分)2019新型冠状病毒(2019﹣nCoV),2020年1月12日被世命名,科学家借助比光学显微镜更加厉害的电子显微镜发现新型冠状病毒的大小约为0.000000125米.则数据0.000000125用科学记数法表示正确的是( )
A.1.25×107 B.1.25×10﹣7 C.1.25×108 D.1.25×10﹣8
【分析】绝对值小于1的负数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.000000125=1.25×10﹣7.
故选:B.
5.(3分)下列说法错误的是( )
A.关于某条直线对称的两个三角形一定全等
B.到线段两端点距离相等的点有无数个
C.等腰三角形的中线、高、角平分线三线合一
D.轴对称图形的对称轴是对称点所连线段的垂直平分线
【分析】根据关于某条直线对称的图形叫轴对称图形,以及等腰三角形的性质分别判断得出答案.
解:A、关于某条直线对称的两个三角形一定全等,正确,不合题意;
B、到线段两端点距离相等的点有无数个,正确,不合题意;
C、等腰三角形底边上的中线、高、角平分线三线合一,故原说法错误,符合题意;
D、轴对称图形的对称轴是对称点所连线段的垂直平分线,正确,不合题意;
故选:C.
6.(3分)如图,已知AB∥CD,直线AB,CD被BC所截,E点在BC上,若∠1=45°,∠2=35°,则∠3=( )
A.65° B.70° C.75° D.80°
【分析】由平行线的性质可求得∠C,在△CDE中利用三角形外的性质可求得∠3.
解:
∵AB∥CD,
∴∠C=∠1=45°,
∵∠3是△CDE的一个外角,
∴∠3=∠C+∠2=45°+35°=80°,
故选:D.
7.(3分)电话卡上存有4元话费,通话时每分钟话费0.4元,则电话卡上的余额y(元)与通话时间t(分钟)之间的函数图象是图中的( )
A. B.
C. D.
【分析】根据当通话时间为0时,余额为4元;当通话时间为10时,余额为0元.据此判断即可.
解:由题意可知:当通话时间为0时,余额为4元;当通话时间为10时,余额为0元.
∴y=4﹣0.4t(0≤t≤10),
故只有选项D符合题意.
故选:D.
8.(3分)已知:如图,在△ABC中,AB=AC,AB的垂直平分线DE,分别交AB,AC于点D,E.若AD=3,BC=5,则△BEC的周长为( )
A.8 B.10 C.11 D.13
【分析】由AB的垂直平分线DE分别交AB、AC于点D、E,易得△EBC的周长=AC+BC;
解:∵AB的垂直平分线DE分别交AB、AC于点D、E,
∴AE=BE,
∵AD=3,
∴AB=6,
∴AE+EC=AC=AB=6,
∵BC=5,
∴△EBC的周长=BC+BE+CE=BC+AE+CE=BC+AC=6+5=11;
故选:C.
9.(3分)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍无法判定△ABE≌△ACD的是( )
A.AD=AE B.∠B=∠C C.CD=BE D.∠ADC=∠AEB
【分析】根据全等三角形的判定方法对各选项进行判断.
解:∵AB=AC,∠BAE=∠CAD,
∴当添加AE=AD时,可根据“SAS”判断△ABE≌△ACD;
当添加∠B=∠C时,可根据“ASA”判断△ABE≌△ACD;
当添加∠AEB=∠ADC时,可根据“AAS”判断△ABE≌△ACD.
故选:C.
10.(3分)如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1B2,△A2B2B3,△A3B3B4,…均为等边三角形.若OB1=1,则△A8B8B9的边长为( )
A.64 B.128 C.132 D.256
【分析】根据等腰三角形的性质以及平行线的性质得出B1A1∥A2B2∥A3B3,以及a2=2a1,得出a3=4a1=4,a4=8a1=8,a5=16a1…进而得出答案.
解:∵△A1B1B2是等边三角形,
∴∠A1B1B2=∠A1B2O=60°,A1B1=A1B2,
∵∠O=30°,
∴∠A2A1B2=∠O+∠A1B2O=90°,
∵∠A1B1B2=∠O+∠OA1B1,
∴∠O=∠OA1B1=30°,
∴OB1=A1B1=A1B2=1,
在Rt△A2A1B2中,∵∠A1A2B2=30°
∴A2B2=2A1B2=2,
同法可得A3B3=22,A4B4=23,…,AnBn=2n﹣1,
∴△A8B8B9的边长=27=128,
故选:B.
二.填空题(每小题3分,共24分)
11.(3分)计算:x(x﹣1)= x2﹣x .
【分析】根据单项式乘多项式法则计算可得.
解:x(x﹣1)=x2﹣x,
故答案为:x2﹣x.
12.(3分)若x+m与2﹣x的乘积中不含x的一次项,则实数m的值为 2 .
【分析】根据多项式乘以多项式的法则,可表示为(a+b)(m+n)=am+an+bm+bn,计算即可.
解:根据题意得:
(x+m)(2﹣x)=2x﹣x2+2m﹣mx,
∵x+m与2﹣x的乘积中不含x的一次项,
∴m=2;
故答案为:2.
13.(3分)如果等腰三角形的一个角是70°,那么它的顶角是 70或40 度.
【分析】由于题中没有明确说明70°是顶角还是底角,故分两种情况考虑:当70°是顶角,显然得到结果;当70°是底角时,根据等腰三角形的性质得到两底角都为70°,利用三角形的内角和定理即可求出此时的顶角.
解:若70°为顶角,则此等腰三角形的顶角是70°;
若70°为底角,则此等腰三角形的顶角为180°﹣2×70°=40°,
综上,此等腰三角形的顶角为70°或40°.
故答案为:70或40
14.(3分)如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,BC=8cm,则DE+DB= 8cm .
【分析】根据角平分线性质得出DE=CD,求出BD+DE=BC,即可得出答案.
解:∵在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,
∴DC=DE,
∵BC=8cm,
∴DE+BD=CD+BD=BC=8cm,
故答案为:8cm.
15.(3分)一辆汽车油箱中现存油50L,汽车每行驶100km耗油10L,则油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是 y=﹣0.1x+50 .
【分析】由于汽车每行驶100km耗油10L,那么汽车行驶路程x千米耗油0.1xL,而汽车油箱中能盛汽油50L,由此即可确定加满油后,油箱中剩余油量y(L)与汽车行驶路程x(km)之间的函数关系式.
解:∵汽车每行驶100km耗油10L,
∴汽车行驶路程xkm耗油0.1xL,
∵汽车油箱中现存油50L,
∴油箱剩余油量y(L)与汽车行驶路程x(km)之间的关系式是y=﹣0.1x+50.
故答案是:y=﹣0.1x+50.
16.(3分)将一张长方形纸条折成如图所示的图形,如果∠1=64°,那么∠2= 58° .
【分析】由折叠可得,∠2=∠CEF,再根据平角的定义,即可得到∠2的度数.
解:由折叠可得,∠2=∠CEF,
∵∠1=64°,
∴∠2=(180°﹣64°)=58°,
故答案为:58°.
17.(3分)如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C= 24 度.
【分析】根据线段的垂直平分线的性质得到EA=EC,得到∠EAC=∠C,根据角平分线的定义、三角形内角和定理计算即可.
解:∵DE是AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C,
∴∠FAC=∠EAC+19°,
∵AF平分∠BAC,
∴∠FAB=∠EAC+19°,
∵∠B+∠BAC+∠C=180°,
∴70°+2(∠C+19°)+∠C=180°,
解得,∠C=24°,
故答案为:24.
18.(3分)如图1,在长方形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P的运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则长方形ABCD的周长是 16 .
【分析】根据函数的图象、结合图形求出AB、BC的值,根据长方形的周长公式得出长方形ABCD的周长.
解:∵动点P从点B出发,沿BC、CD、DA运动至点A停止,而当点P运动到点C,D之间时,△ABP的面积不变,
函数图象上横轴表示点P运动的路程,x=4时,y开始不变,说明BC=3,x=8时,接着变化,说明CD=8﹣3=5,
∴AB=5,BC=3,
长方形ABCD的周长是:2(AB+BC)=16,
故答案为:16
三.解答题(共46分)
19.(9分)(1)计算:(﹣1)﹣3+(2019﹣π)0﹣|﹣5|;
(2)先化简,再求值:[(x﹣2y)2﹣(3y+x)(x﹣3y)+3y2]÷4y,其中x=2,y=1.
【分析】(1)先根据负整数指数幂,零指数幂,绝对值进行计算,再求出即可;
(2)先算括号内的乘法,再合并同类项,算除法,最后代入求出即可.
解:(1)(﹣1)﹣3+(2019﹣π)0﹣|﹣5|
=﹣1+1﹣5
=﹣5;
(2)[(x﹣2y)2﹣(3y+x)(x﹣3y)+3y2]÷4y
=(x2﹣4xy+4y2﹣x2+9y2+3y2)÷4y
=(16y2 ﹣4xy)÷4y
=4y﹣x,
当x=2,y=1时,原式=4×1﹣2=2.
20.(6分)已知:如图,AE平分∠BAC,CE平分∠ACD,且∠a+∠β=90°.
求证:AB∥CD.
【分析】根据角平分线的定义和平行线的判定定理即可得到结论.
【解答】证明:∵CE平分∠ACD,
∴∠ACD=2∠α.
∵AE平分∠BAC,
∴∠BAC=2∠β,
∴∠ACD+∠BAC=2∠α+2∠β.
即∠ACD+∠BAC=2(∠α+∠β).
∵∠α+∠β=90°,
∴∠ACD+∠BAC=180°,
∴AB∥CD.
21.(8分)如图描述了一辆汽车在某一直路上的行驶过程,汽车离出发地的距离s(km)和行驶时间t(h)之间的关系,请根据图象回答下列问题:
(1)汽车共行驶的路程是多少?
(2)汽车在行驶途中停留了多长时间?
(3)汽车在每个行驶过程中的速度分别是多少?
(4)汽车到达离出发地最远的地方后返回,则返回用了多长时间?
【分析】(1)观察函数图象的纵坐标,可得汽车行驶的路程;
(2)观察函数图象,可得平行于t轴的线段;
(3)分四种情形分别求解.
(4)观察函数图象的横坐标,可得到达最远地方的时间,回到出发点的时间,根据有理数的减法,可得答案.
解:(1)由纵坐标看出汽车最远行驶路程是120千米,往返共行驶的路程是120×2=240千米;
(2)由横坐标看出,2﹣1.5=0.5,汽车在行驶途中停留了0.5小时;
(3)线段AB上的速度为:千米/小时,线段BC上的速度为0,线段CD上的速度为40千米/小时,线段DE上的速度为:80千米/小时.
(4)由横坐标看出4.5﹣3=1.5,返回用了1.5小时.
22.(8分)如图,在四边形ABCD中,AB=BC,BF平分∠ABC,AF∥DC,连接AC,CF.
求证:(1)AF=CF;(2)CA平分∠DCF.
【分析】(1)根据BF平分∠ABC?∠ABF=∠CBF,再加上AB=BC,BF=BF就可以推出△ABF≌△CBF,依据全等三角形对应边相等的性质可以推出AF=CF;
(2)根据(1)中所得出的结论可以推出∠FCA=∠FAC;依据平行线的性质可以得出内错角∠FAC、∠DCA相等,等量代换后,就可推出CA平分∠DCF.
【解答】证明:如图.
(1)∵BF平分∠ABC,
∴∠ABF=∠CBF.(1分)
在△ABF与△CBF中,
∴△ABF≌△CBF(SAS).(2分)
∴AF=CF.(3分)
(2)∵AF=CF,
∴∠FCA=∠FAC.(4分)
∵AF∥DC,
∴∠FAC=∠DCA.
∴∠FCA=∠DCA,即CA平分∠DCF.(5分)
23.(6分)甲、乙两人玩赢卡片游戏,工具是一个如图所示的转盘(等分成8份),游戏规定:自由转动的转盘,当转盘停止后指针指向字母“A”,则甲输给乙2张卡片,若指针指向字母“B”,则乙输给甲3张卡片;若指针指向字母“C”,则乙输给甲1张卡片(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止).
(1)转动一次转盘,求甲赢取1张卡片的概率;
(2)转动一次转盘,求乙赢取2张卡片的概率;
(3)转动一次转盘,求甲赢取卡片的概率.
【分析】根据已知条件得出共有8种等可能的结果,甲赢取卡片有4种结果,乙赢取卡2张片有4种结果,甲赢取卡1张片有3种结果,再根据概率公式即可求出(1)(2)(3).
解:共有8种等可能的结果,甲赢取卡片有4种结果,乙赢取卡2张片有4种结果,甲赢取卡1张片有3种结果,
(1)甲赢取1张卡片的概率是:P(甲赢取1张卡片)=;
(2)乙赢取2张卡片的概率是:P(乙赢取2张卡片)==;
(3)甲赢取卡片的概率是:P(甲赢取卡片)==;
24.(9分)如图,点D在射线BC上运动,△ABC与△ADE都是以点A为直角顶点的等腰直角三角形.
(1)在图1中找出一对全等三角形并说明理由;
(2)试在图1中说明EC⊥BC;
(3)如图2,当点D在BC的延长线上时,若BC=6,BD=x(x>6),△CDE的面积为y,试求出y与x之间的关系式.
【分析】(1)根据等腰直角三角形的性质得到∠BAC=90°,∠DAE=90°,AB=AC,AD=AE,利用SAS定理证明△ABD≌△ACE;
(2)根据等腰直角三角形的性质、全等三角形的性质解答;
(3)证明△ABD≌△ACE,根据全等三角形的性质得到BD=EC,∠ACE=∠B=45°,根据三角形的面积公式计算,求出y与x之间的关系式.
解:(1)△ABD≌△ACE.
理由如下:∵△ABC与△ADE都是以点A为直角顶点的等腰直角三角形,
∴∠BAC=90°,∠DAE=90°,AB=AC,AD=AE,
∴∠BAD+∠DAC=∠CAE+∠DAC=90°,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS);
(2)证明:∵△ABD≌△ACE,
∴∠ACE=∠B=45°.
∵∠ACB=45°,
∴∠ECD=90°,
∴EC⊥BC;
(3)解:∵∠BAD+∠DAC=∠CAE+∠DAC=90°,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=EC,∠ACE=∠B=45°,
∵∠ACB=45°,
∴∠ECD=90°,
∴EC⊥BC,
∴S△ECD=CD?EC,
∴y=(x﹣6)?x=x2﹣3x(x>6).
同课章节目录
