2.7.1 有理数的乘法教学课件(共26张PPT)
文档属性
| 名称 | 2.7.1 有理数的乘法教学课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
北师大版
初中数学
北师大版七年级数学(上册)
第二章
有理数及其运算
2.6有理数的乘法法则
第一课时
学习目标
1.掌握有理数的乘法法则并能进行熟练地运算.
(重点)
2.掌握多个有理数相乘的积的符号法则.
(难点)
创设情境
甲水库
乙水库
甲水库的水位每天上升3cm,乙水库的水位每天下降3cm,
4天后甲、乙水库的总变化量各是多少?
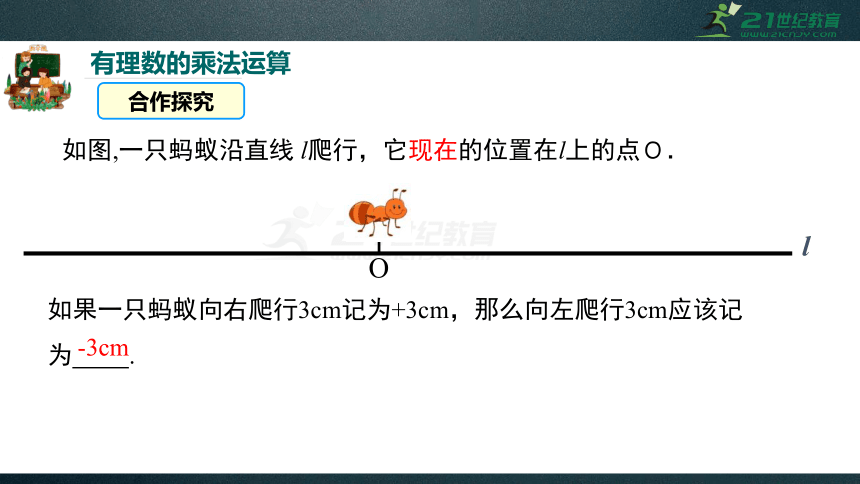
如图,一只蚂蚁沿直线
l爬行,它现在的位置在l上的点O.
l
O
如果一只蚂蚁向右爬行3cm记为+3cm,那么向左爬行3cm应该记为
.
-3cm
有理数的乘法运算
合作探究
探究1:
(+3)
×
(+4)=?
(+3)
:看作蚂蚁向右运动3米;
×
(+4)
:看作蚂蚁沿原方向运动4次;
结果:蚂蚁向右运动12米.
12
+3
一次
用乘法表示为:
(+3
)
×
(+4
)
=
+12
0
3
12
9
6
二次
三次
四次
探究2:
(-3)
×
(+4)=?
(-3)
:看作蚂蚁向左运动3米;
×
(+4)
:看作蚂蚁沿原方向运动4次
结果:蚂蚁向左运动12米.
-12
-3
一次
用乘法表示为:
(-3
)
×
(+4
)
=
-12
0
-9
-12
-3
-6
二次
三次
四次
3
×
4
=
12
(-3)×
4
=
-12
一个因数换成相反数
积是原来的积的相反数
发现:两数相乘,把一个因数换成它的相反数,所得的积是原来积的相反数.
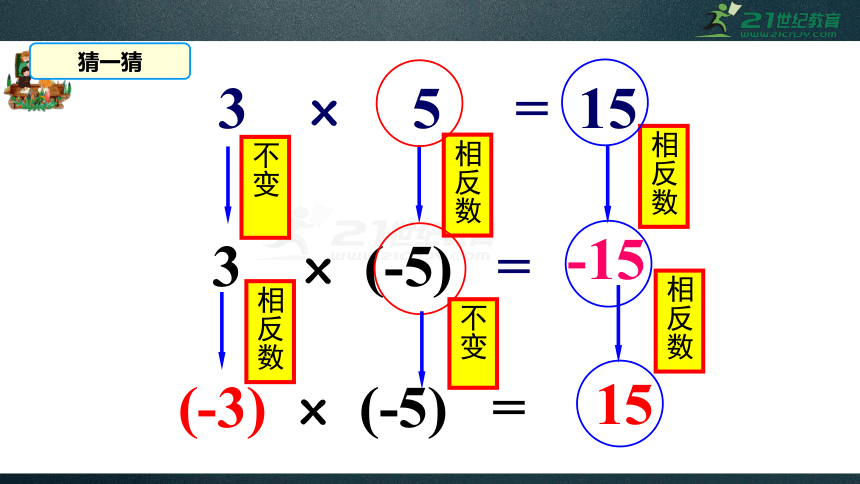
议一议
3
×
5
=
15
3
×
(-5)
=
-15
(-3)
×
(-5)
=
15
相反数
猜一猜
相反数
不变
相反数
不变
相反数
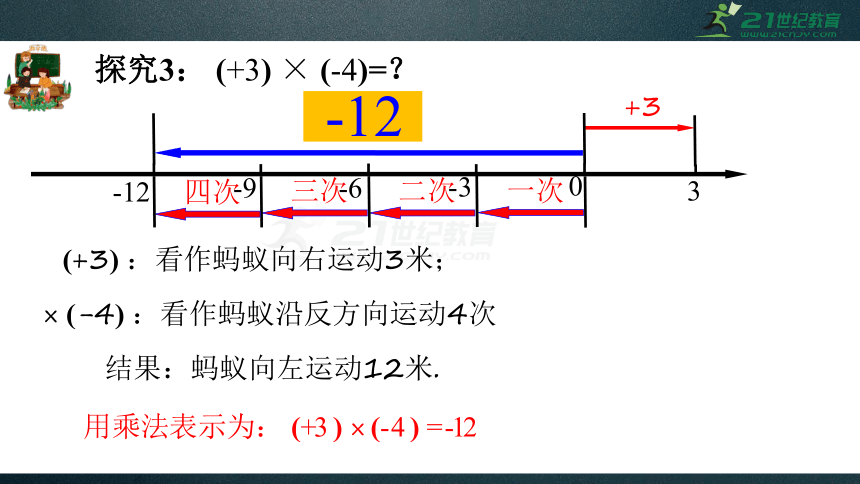
探究3:
(+3)
×
(-4)=?
(+3)
:看作蚂蚁向右运动3米;
×
(-4)
:看作蚂蚁沿反方向运动4次
结果:蚂蚁向左运动12米.
用乘法表示为:
(+3
)
×
(-
4
)
=
-12
+3
-12
一次
3
0
-9
-12
-3
-6
二次
三次
四次
探究4:
(-3)
×
(-4)=?
(-3)
:看作蚂蚁向左运动3米;
×
(-4)
:看作蚂蚁沿反方向运动4次
结果:蚂蚁向右运动12米.
12
+3
一次
用乘法表示为:
(-3
)
×
(-4
)
=
+12
二次
三次
四次
0
3
12
9
6
-3
探究5:
(1)
0
×
4
=
0
在原地运动4次
(2)
(
-3
)
×0
=
0
向左运动0次
(3)
0×
0
=
0
结论:被乘数是0或者乘数是0,结果仍在原处.
总结归纳
相同符号的两个数相乘,得
到是正数,并把绝对值相乘.
不同符号的两个数相乘,得
到是负数,并把绝对值相乘.
一个数与0相乘或0
与一个数相乘积为0.
(1)(+3)×(+4)=+12
(2)(-3)×(-4)=+12
}
(3)(-3)×(+4)=-12
(4)(+3)×(-4)=-12
}
(5)0×(-4)=0,
3×0=0
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与0相乘,积仍为0.
确定下列积的符号:
(1)
6×
(
-18
)
(2)
(
-3
)
×12
(3)
(
+21
)
×
(
+15
)
(4)
(
-0.96
)
×
(
-0.72
)
积的符号为负
积的符号为负
积的符号为正
积的符号为正
试一试
特别提醒:乘法运算时,
一定要先确定积的
符号,再将绝对值相乘!
?
?
例1计算:
例题讲解
注意哟:乘法运算时,
一定要先确定积的
符号,再算绝对值!
(异号得负,绝对值相乘)
(同号得正,绝对值相乘)
(同号得正,绝对值相乘)
(同号得正,绝对值相乘)
倒数定义:如果两个有理数的乘积为1,
那么称其中的一个是另一个的倒数.也
称这两个有理数互为倒数.
所有有理数都有倒数吗?
探究新知
=
1
;
=
1
.
我们称
的倒数,或者
互为倒数.
知识运用
做一做:1、求下列数的倒数
原数
1
-1
-9
倒数
2、0的倒数为
零没有倒数
3、议一议a的倒数是
对吗?
(a≠0时,a的倒数是
)
(2)
若是带分数必须化成假分数,然后把假分数的分子,
分母颠倒位置即可;
1、互为倒数的两个数符号相同,即正数的倒数是正数,负数的倒数是负数;
求倒数的时候要注意:
2、求分数的倒数(1)若是真分数的倒数是分子与分母颠倒位置;
3、0没有倒数.
探求新知
(3)若是小数,先将其化成分数,再求倒数;
观察下列各式,判断他们积的符号:
(1)(-1)×2×3×4
(2)(-1)×(-2)×3×4
(3)(-1)×(-2)×(-3)×4
(4)(-1)×(-2)×(-3)×(-4)
(5)(-1)×(-2)×(-3)×(-4)×0
知识拓展
规律:若干个不为零的因数相乘,当负因数个数为偶
数个时,积为正,当负因数个数为奇数个时,积为负.
几个因数相乘,若有一个因数为零,则积为零
你能说出积的
符号的规律
吗?
积的符号为负
积的符号为正
积的符号为负
积的符号为正
积为0
例题讲解
例2计算:
趁热打铁
3.3
4.7
-2.6
-5.1
×(-4)
1、把下图中第一个图内的每个数分别乘
-4,将结果写在第二个图内相应的位置.
2、计算:
=-22
=0
-13.2
-18.8
10.4
20.4
课堂小结
一般法则:两数相乘,同号得正,异号得负,并把绝对值相乘.
特殊:任何数同0相乘,都得0.
倒数:乘积为1的两个数互为倒数.
应用:
有理数乘法法则
被乘数
乘数
积的符号
积的绝对值
结果
-6
5
12
7
-35
-8
6
-15
0
-56
31
0
1.完成下表
-
30
-30
+
84
84
+
280
280
-
90
-90
挑战自我,思维拓展
2.填空(用“>”或“<”号连接):
(1)如果
m>0,n<0
,那么mn___0;
(2)如果
m<0,n<0
,那么mn
___0.
>
<
0
0
0
0
3.
若
ab>0,则必有
(
)
A.
a>0,b>0
B.
a<0
,
b<0
C.
a>0
,
b<0
D.
a>0
,
b>0或a<0
,
b<0
4.若ab=0
,则一定有(
)
a=b=0
B.
a,b至少有一个为0
C.
a=0
D.
a,b最多有一个为0
D
B
5.一个有理数和它的相反数之积(
)
A.
一定是正数
B.
一定是负数
C.
非负数
D.
非正数
D
6.若ab=|ab|,则必有(
)
a与b同号
B.
a与b异号
C.
a与b中至少有一个等于0
D.
以上都不对
D
7.
规定气温的变化量,上升为正,下降为负.某登山队攀登一座山峰,每登高1km,气温的变化量为-3.5℃,攀登4km后,气温有什么变化?
解:(-3.5)×4=-13
答:气温下降13℃.
8.把
-18
表示成两个整数的积,有多少种可能性?把它们全部写
出来.
解:-1
×18=-18,
1
×(-18)=-18,
-2
×9=-18,
2
×(-9)=-18,
-3
×6=-18,
3
×(-6)=-18
别忘记了作业
北师大版
初中数学
北师大版七年级数学(上册)
第二章
有理数及其运算
2.6有理数的乘法法则
第一课时
学习目标
1.掌握有理数的乘法法则并能进行熟练地运算.
(重点)
2.掌握多个有理数相乘的积的符号法则.
(难点)
创设情境
甲水库
乙水库
甲水库的水位每天上升3cm,乙水库的水位每天下降3cm,
4天后甲、乙水库的总变化量各是多少?
如图,一只蚂蚁沿直线
l爬行,它现在的位置在l上的点O.
l
O
如果一只蚂蚁向右爬行3cm记为+3cm,那么向左爬行3cm应该记为
.
-3cm
有理数的乘法运算
合作探究
探究1:
(+3)
×
(+4)=?
(+3)
:看作蚂蚁向右运动3米;
×
(+4)
:看作蚂蚁沿原方向运动4次;
结果:蚂蚁向右运动12米.
12
+3
一次
用乘法表示为:
(+3
)
×
(+4
)
=
+12
0
3
12
9
6
二次
三次
四次
探究2:
(-3)
×
(+4)=?
(-3)
:看作蚂蚁向左运动3米;
×
(+4)
:看作蚂蚁沿原方向运动4次
结果:蚂蚁向左运动12米.
-12
-3
一次
用乘法表示为:
(-3
)
×
(+4
)
=
-12
0
-9
-12
-3
-6
二次
三次
四次
3
×
4
=
12
(-3)×
4
=
-12
一个因数换成相反数
积是原来的积的相反数
发现:两数相乘,把一个因数换成它的相反数,所得的积是原来积的相反数.
议一议
3
×
5
=
15
3
×
(-5)
=
-15
(-3)
×
(-5)
=
15
相反数
猜一猜
相反数
不变
相反数
不变
相反数
探究3:
(+3)
×
(-4)=?
(+3)
:看作蚂蚁向右运动3米;
×
(-4)
:看作蚂蚁沿反方向运动4次
结果:蚂蚁向左运动12米.
用乘法表示为:
(+3
)
×
(-
4
)
=
-12
+3
-12
一次
3
0
-9
-12
-3
-6
二次
三次
四次
探究4:
(-3)
×
(-4)=?
(-3)
:看作蚂蚁向左运动3米;
×
(-4)
:看作蚂蚁沿反方向运动4次
结果:蚂蚁向右运动12米.
12
+3
一次
用乘法表示为:
(-3
)
×
(-4
)
=
+12
二次
三次
四次
0
3
12
9
6
-3
探究5:
(1)
0
×
4
=
0
在原地运动4次
(2)
(
-3
)
×0
=
0
向左运动0次
(3)
0×
0
=
0
结论:被乘数是0或者乘数是0,结果仍在原处.
总结归纳
相同符号的两个数相乘,得
到是正数,并把绝对值相乘.
不同符号的两个数相乘,得
到是负数,并把绝对值相乘.
一个数与0相乘或0
与一个数相乘积为0.
(1)(+3)×(+4)=+12
(2)(-3)×(-4)=+12
}
(3)(-3)×(+4)=-12
(4)(+3)×(-4)=-12
}
(5)0×(-4)=0,
3×0=0
有理数乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与0相乘,积仍为0.
确定下列积的符号:
(1)
6×
(
-18
)
(2)
(
-3
)
×12
(3)
(
+21
)
×
(
+15
)
(4)
(
-0.96
)
×
(
-0.72
)
积的符号为负
积的符号为负
积的符号为正
积的符号为正
试一试
特别提醒:乘法运算时,
一定要先确定积的
符号,再将绝对值相乘!
?
?
例1计算:
例题讲解
注意哟:乘法运算时,
一定要先确定积的
符号,再算绝对值!
(异号得负,绝对值相乘)
(同号得正,绝对值相乘)
(同号得正,绝对值相乘)
(同号得正,绝对值相乘)
倒数定义:如果两个有理数的乘积为1,
那么称其中的一个是另一个的倒数.也
称这两个有理数互为倒数.
所有有理数都有倒数吗?
探究新知
=
1
;
=
1
.
我们称
的倒数,或者
互为倒数.
知识运用
做一做:1、求下列数的倒数
原数
1
-1
-9
倒数
2、0的倒数为
零没有倒数
3、议一议a的倒数是
对吗?
(a≠0时,a的倒数是
)
(2)
若是带分数必须化成假分数,然后把假分数的分子,
分母颠倒位置即可;
1、互为倒数的两个数符号相同,即正数的倒数是正数,负数的倒数是负数;
求倒数的时候要注意:
2、求分数的倒数(1)若是真分数的倒数是分子与分母颠倒位置;
3、0没有倒数.
探求新知
(3)若是小数,先将其化成分数,再求倒数;
观察下列各式,判断他们积的符号:
(1)(-1)×2×3×4
(2)(-1)×(-2)×3×4
(3)(-1)×(-2)×(-3)×4
(4)(-1)×(-2)×(-3)×(-4)
(5)(-1)×(-2)×(-3)×(-4)×0
知识拓展
规律:若干个不为零的因数相乘,当负因数个数为偶
数个时,积为正,当负因数个数为奇数个时,积为负.
几个因数相乘,若有一个因数为零,则积为零
你能说出积的
符号的规律
吗?
积的符号为负
积的符号为正
积的符号为负
积的符号为正
积为0
例题讲解
例2计算:
趁热打铁
3.3
4.7
-2.6
-5.1
×(-4)
1、把下图中第一个图内的每个数分别乘
-4,将结果写在第二个图内相应的位置.
2、计算:
=-22
=0
-13.2
-18.8
10.4
20.4
课堂小结
一般法则:两数相乘,同号得正,异号得负,并把绝对值相乘.
特殊:任何数同0相乘,都得0.
倒数:乘积为1的两个数互为倒数.
应用:
有理数乘法法则
被乘数
乘数
积的符号
积的绝对值
结果
-6
5
12
7
-35
-8
6
-15
0
-56
31
0
1.完成下表
-
30
-30
+
84
84
+
280
280
-
90
-90
挑战自我,思维拓展
2.填空(用“>”或“<”号连接):
(1)如果
m>0,n<0
,那么mn___0;
(2)如果
m<0,n<0
,那么mn
___0.
>
<
0
0
0
0
3.
若
ab>0,则必有
(
)
A.
a>0,b>0
B.
a<0
,
b<0
C.
a>0
,
b<0
D.
a>0
,
b>0或a<0
,
b<0
4.若ab=0
,则一定有(
)
a=b=0
B.
a,b至少有一个为0
C.
a=0
D.
a,b最多有一个为0
D
B
5.一个有理数和它的相反数之积(
)
A.
一定是正数
B.
一定是负数
C.
非负数
D.
非正数
D
6.若ab=|ab|,则必有(
)
a与b同号
B.
a与b异号
C.
a与b中至少有一个等于0
D.
以上都不对
D
7.
规定气温的变化量,上升为正,下降为负.某登山队攀登一座山峰,每登高1km,气温的变化量为-3.5℃,攀登4km后,气温有什么变化?
解:(-3.5)×4=-13
答:气温下降13℃.
8.把
-18
表示成两个整数的积,有多少种可能性?把它们全部写
出来.
解:-1
×18=-18,
1
×(-18)=-18,
-2
×9=-18,
2
×(-9)=-18,
-3
×6=-18,
3
×(-6)=-18
别忘记了作业
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
