2020-2021学年度沪教版数学六年级上册讲义:期中复习(教师版)
文档属性
| 名称 | 2020-2021学年度沪教版数学六年级上册讲义:期中复习(教师版) |
|
|
| 格式 | docx | ||
| 文件大小 | 664.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-13 00:00:00 | ||
图片预览





文档简介
期中复习
内容分析
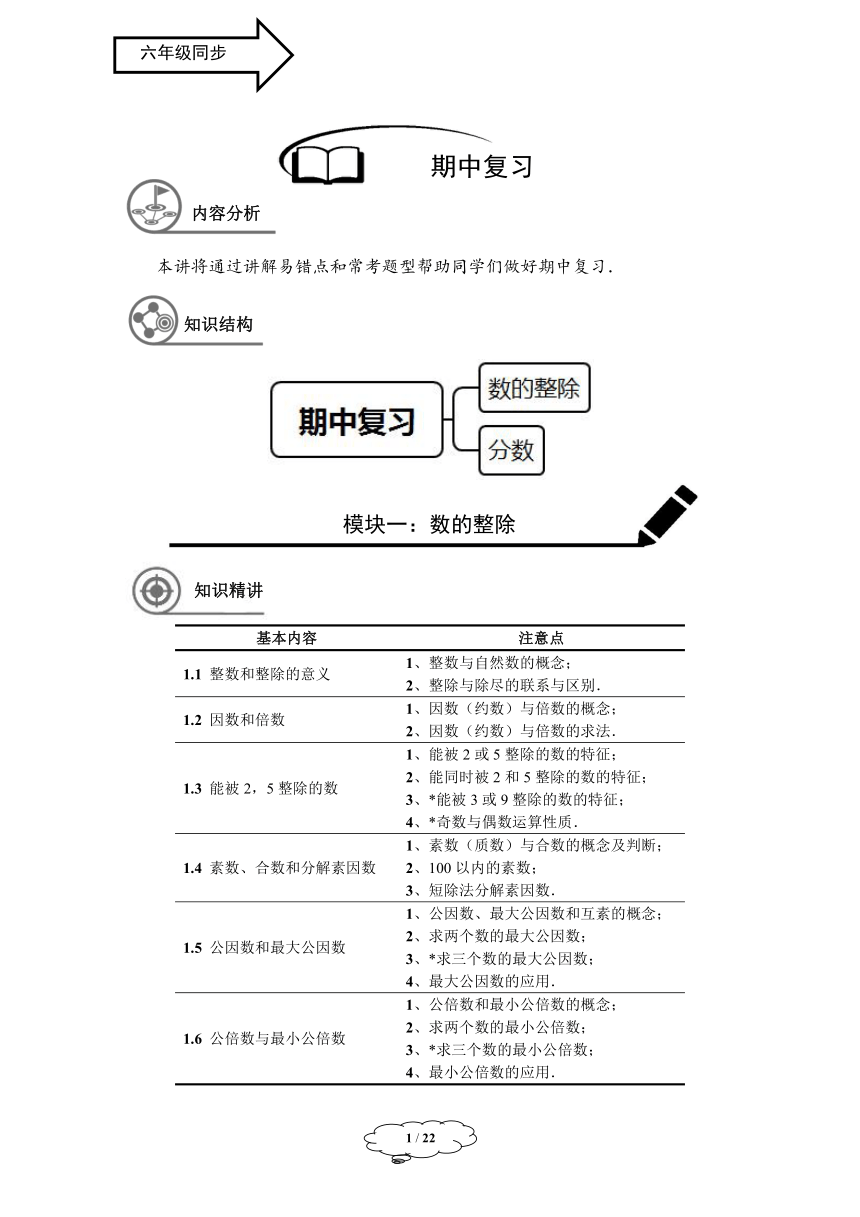
本讲将通过讲解易错点和常考题型帮助同学们做好期中复习.
知识结构
1209675215900
模块一:数的整除
知识精讲
基本内容
注意点
1.1 整数和整除的意义
1、整数与自然数的概念;
2、整除与除尽的联系与区别.
1.2 因数和倍数
1、因数(约数)与倍数的概念;
2、因数(约数)与倍数的求法.
1.3 能被2,5整除的数
1、能被2或5整除的数的特征;
2、能同时被2和5整除的数的特征;
3、*能被3或9整除的数的特征;
4、*奇数与偶数运算性质.
1.4 素数、合数和分解素因数
1、素数(质数)与合数的概念及判断;
2、100以内的素数;
3、短除法分解素因数.
1.5 公因数和最大公因数
1、公因数、最大公因数和互素的概念;
2、求两个数的最大公因数;
3、*求三个数的最大公因数;
4、最大公因数的应用.
1.6 公倍数与最小公倍数
1、公倍数和最小公倍数的概念;
2、求两个数的最小公倍数;
3、*求三个数的最小公倍数;
4、最小公倍数的应用.
例题解析
概念辨析判断:
(1)最大的正整数和最大的负整数都不存在.( )
(2)a除以b,如果除得的商是整数且余数为零,我们就说a能被b整除.( )
(3)任何正整数都能被0整除.( )
(4),则n一定能整除m.( )
(5)能同时被6,8整除的数一定能被48整除.( )
(6)一个正整数至少有两个因数.( )
(7)一个正整数的倍数一定能被它的因数整除.( )
(8)奇数的因数一定是奇数.( )
(9)两个正整数的和或差的奇偶性相同.( )
(10)两个偶数的积是偶数,两个偶数的商也是偶数.( )
(11)两个素数的和一定是偶数.( )
(12)两个连续素数的乘积一定是奇数.( )
(13)两个连续正整数的和一定是素数.( )
(14)一个合数至少有三个因数.( )
(15)最小的自然数,最小的质数,最小的合数的和是7.( )
(16)两个不同的素数一定互素.( )
(17)如果两个整数的公因数是1,则这两个数一定互素.( )
(18)7能整除a,又是b的最小倍数,所以a和b的最大公因数是7.( )
(19)正整数a、b,若,那么a、b的最大公因数是4.( )
(20)36和48的公因数共有6个.( )
(21)两个正整数的最大公因数一定能整除这两个数.( )
(22)若(a、b、c都是正整数),则a与b的最大公因数是c.( )
(23)若,则两个正整数m、n的最小公倍数是m.( )
(24)几个正整数的最大公因数一定比它们的最小公倍数小.( )
(25)若三个正整数只有公因数1,则这三个数两两互素.( ).
【难度】★
【答案】××××√ √√√√× ×××√× √√√×√ √××√×
【解析】整除的意义、因数和倍数、分解素因数等相关知识点的理解和应用.
【总结】考查数的整除中相关概念的理解和辨析.
写出50以内的所有素数_______________________________.
【难度】★
【答案】2,3,5,7,11,13,17,19,23,29,31,37,41,43,47.
【解析】素数的因数只有1和它本身.
【总结】考查素数的概念.
能整除24的数有________________.
【难度】★
【答案】1,2,3,4,6,8,12,24.
【解析】本题即求24的因数有哪些.
【总结】考查整除的意义.
在1~100这100个整数中,有25个素数,则合数有______个.
【难度】★
【答案】74.
【解析】.
【总结】注意“1”既不是素数也不是合数.
将342分解素因数为________________________________.
【难度】★
【答案】.
【解析】分解素因数是将一个合数分解成几个素数乘积的形式,注意书写格式.
【总结】本题主要考查分解素因数的概念.
,则m的因数有______个.
【难度】★★
【答案】16.
【解析】法一:,120的因数有16个;
法二:,则m的因数有个.
【总结】考查求一个数的因数有多少的方法.
既是160的因数,又能被2整除的正整数有______个.
【难度】★★
【答案】10.
【解析】160的因数有12个,除了1和5不能被2整除,其它均可.
【总结】考查因数和整除的概念.
从0、1、2、5四个数字中选三个数字组成的数字不重复的三位数,其中,偶数有______个,能被5整除的数有______个,能被5整除的偶数有______个.
【难度】★★
【答案】10;10;6.
【解析】从0、1、2、5四个数字中选三个数字组成的数字不重复的三位数一共有18个,列举即可.
【总结】考查偶数、能被5整除的数的特征.
已知这个数,在内填上一个数字,若要使这个数能被3整除,应填_______________,若要使这个数能被9整除,应填________________.
【难度】★★
【答案】1或4或7; 4.
【解析】2+5+7+9=23,要使这个数能被3整除,则23+的数的和是3的倍数;要使这个
数能被9整除,则23+的数的和是9的倍数.
【总结】考查能被3、9整除的数的特征.
150和125共有的素因数是______________.
【难度】★★
【答案】5,5.
【解析】;125=.
【总结】考查求两个数共有的素因数的方法,注意重复的素因数也要全部写出.
求下列各组数的最大公因数和最小公倍数.
(1)187和442; (2)36、84和39.
【难度】★★
【答案】(1) 17,4862;(2)3,3276.
【解析】(1) ;
所以最大公因数17; 最小公倍数.
(2).
所以最大公因数3; 最小公倍数.
【总结】考查求两个(三个)数的最大公因数和最小公倍数的方法.
先填空,再找规律:
(1)15和6的最大公因数是______,最小公倍数是______,15和6的积是______,它们的最大公因数和最小公倍数的积是______.
(2)从上面的题目中,你发现了什么规律?
(3)根据你发现的规律填空:
甲、乙两数的最大公因数是3,最小公倍数是90,若甲数是18,则乙数是______.
【难度】★★
【答案】(1) 3,30,90, 90;
(2) 两数的最大公因数和最小公倍数的乘积等于这两数的积.
(3) 15.
【解析】(1) ;(2)找规律;(3) .
【总结】考查两数的最大公因数、最小公倍数与两数乘积的关系.
有铅笔433支,橡皮260块,平均分给若干学生,学生数在30~50之间,最后剩余铅笔13支、橡皮8块,问学生究竟有多少人?
【难度】★★★
【答案】42.
【解析】 .
学生数在30~50之间的公因数为42.
【总结】考查在限定条件下求公因数.
黄老师在学校的暖棚里培育花苗,她先每隔20厘米挖一个洞,准备载入花苗,当挖好31个洞时,觉得花苗之间间隔大小,于是决定改为每隔30厘米栽一个花苗。那么有多少个洞需要填埋好?
【难度】★★★
【答案】20.
【解析】20和30的最小公倍数是60,已经挖好的总长度为cm;
不需要填平的洞为:,所以需要填埋好的洞为:个.
【总结】考查种树问题,树的棵数=间隔数+1.
一个正整数被4除余3,被6除余5,被9除余8,则这个数最小是多少?
【难度】★★★
【答案】35.
【解析】4、6、9的最小公倍数是36,则这个数为35.
【总结】考查对最小公倍数的理解.
公共汽车总站有三条线路,第一条每8分钟发一辆车,第二条每10分钟发一辆车,第三条每16分钟发一辆车,早上6:00三条路线同时发出第一辆车,该总站发出最后一辆车是20:00,求该总站最后一次三辆车同时发出的时刻.
【难度】★★★
【答案】19:20.
【解析】8、10、16的最小公倍数是80,6:00—20:00共14小时,
分钟,20:00的前40分钟即为19:20.
【总结】考查发车间隔问题,关键是求出每一次同时发车的周期.
模块二:分数
知识精讲
基本内容
注意点
2.1 分数与除法
1、分数的概念和意义;
2、分数与除法的关系.
2.2 分数的基本性质
1、基本性质;
2、最简分数的概念与约分.
2.3 分数的大小比较
1、公分母与分数的通分;
2、分数比较大小的基本方法;
3、*分数比较大小的特殊方法.
2.4 分数的加减法
1、分数加减法的计算法则;
2、真分数、假分数、带分数的概念及运算;
3、分数加减法的应用.
2.5 分数的乘法
1、分数乘法的计算法则;
2、分数乘法的应用.
2.6 分数的除法
1、分数除法的计算法则;
2、倒数的概念;
3、分数除法的应用.
2.7 分数与小数互化
1、分数化为小数的方法;
2、可化为有限小数的分数的特征;
3、有限小数化为分数的方法;
4、循环小数的相关概念;
5、*循环小数化为分数的技巧.
2.8 分数小数的四则混合运算
1、分数小数混合运算时互化的原则;
2、常见的分数与小数的互化;
3、*速算与巧算.
2.9 分数运算的应用
1、一个数是另一个数的几分之几;
2、一个数的几分之几是多少;
3、已知一个数的几分之几,求这个数;
4、一个数比另一个数多(或)少几分之几;
5、*工程问题.
例题解析
概念辨析判断:
(1)如果a、b是正整数,则;( )
(2)因为,所以除法就是分数;( )
(3)把一个蛋糕分给10个小朋友,则每人能获得这个蛋糕的;( )
(4)分子、分母都是正整数,且由奇数和偶数组成的分数是最简分数;( )
(5)若a、b、n都是正整数,则;( )
(6)分数的分子分母同时加上或减去一个不为零的相同的数,分数的大小一定改变;( )
(7)约分就是将一个分数的分子与分母的最大公因数约去的过程;( )
(8)约分后是,约分后可得;( )
(9)若是真分数,而是假分数,则正整m = 6;( )
(10)任何一个正整数,除以一个真分数,所得的数一定比原数大;( )
(11)任何一个正整数,乘以一个假分数,所得的数一定比原数大;( )
(12)若,则a和b互为倒数;( )
(13)除以一个数的倒数,等于乘以这个数;( )
(14)1.5的与500的相等;( )
(15)一袋面粉,第一天用去,第二天用去,此时还剩下千克;( )
(16)甲数比乙数多,则乙数比甲数少.( )
【难度】★
【答案】××××× ×√××√ ×√√√× √
【解析】分数与除法的关系,分数的几分之几的意义等.
【总结】考查对分数基本概念性质等理解.
写出下列各图形中阴影部分是整体的几分之几.
41910089535
______; ______; ______.
【难度】★
【答案】.
【解析】利用图形的割补即得.
【总结】考查对分数意义的理解.
一本80页的书,小红第一天读26页,第二天读32页,未读的页数是总页数的______.
【难度】★
【答案】.
【解析】.
【总结】考查一个数是另一个数的几分之几.
.
【难度】★
【答案】18,42,42.
【解析】分数的分子和分母同时乘以一个不为0的数,分数的值不变.
【总结】考查分数和除法的关系,分数的基本性质.
分数中的a和b同时缩小为原来的,得到的分数是原来的( )
A. B. C.3倍 D.9倍
【难度】★
【答案】A.
【解析】.
【总结】考查分数的性质.
下列说法中正确的有( )个
(1)最简分数的分子和分母没有公因数;
(2)一个分数,分子扩大到原来的4倍,分母缩小到原来的一半,此分数就扩大2倍;
(3)分数就是两个正整数相除的商;
(4)做同一个零件,王师傅3小时做22个,李师傅4小时35分钟做33个,张师傅90分钟做13个,则张师傅的效率最高.
A.0 B.1 C.2 D.3
【难度】★★
【答案】B
【解析】(1) 有公因数1;(2) 此分数就扩大8倍;(3) 表述不对. 应为:两个正整数相除
的商可以用分数表示.(4) 正确
【总结】考查分数中的相关概念的理解.
6
A
B
C
1
2
3
4
5
0
(1)指出数轴上A、B、C各点分别表示什么数?
A:______;B:______;C:______.
(2)用数轴上的点表示分数和.
1
2
3
4
5
0
6
【难度】★★
【答案】(1) A:______;B:______;C:__3____.
5143503810(2)
【解析】分数在数轴上的表示如图.
【总结】考查分数在数轴上的表示.
分数的值小于1且分母是100的最简分数有______个.
【难度】★★
【答案】40.
【解析】当分子小于100,且个位数是1、3、7、9时符合题意.共有个.
【总结】考查最简分数的意义.
,括号中能填的正整数有______个.
【难度】★★
【答案】51.
【解析】原式可化为: ;.
【总结】考查分数的性质.
比较大小:______,______,______.
【难度】★★
【答案】>、<、>.
【解析】(1) 分子相同,分母大的反而小;
(2) ;
(3)
【总结】考查比较分数大小.
在分数、、、中能化为有限小数的是____________.
【难度】★★
【答案】、.
【解析】当一个分数化成最简分数后,若分母的因数中只有2和5,则这个分数可化为有限小数.
【总结】考查分数能化为有限小数的条件.
下列正确的有( )个
;;;.
A.1 B.2 C.3 D.4
【难度】★★
【答案】B
【解析】①④正确.
【总结】考查分数的性质.
计算:
(1)(结果化为假分数);
(2)(结果化为带分数);
(3);
(4);
(5);
(6).
【难度】★★
【答案】(1) ;(2) ;(3) ;(4) ;(5);(6).
【解析】(1) 原式=;
(2) 原式=;
(3) 原式=;
(4) ;
(5) 原式===;
(6) 原式==.
【总结】考查分数的混合运算,注意运算法则的准确运用,能巧算时要巧算.
某初级中学男女生人数情况如图,看图回答:(填几分之几)
(1)全校男生人数是全校学生数的____________;
(2)全校女生人数是全校男生人数的____________;
(3)八年级女生人数比八年级男生人数少____________;
(4)七年级男生人数比七年级女生人数多____________;
(5)六年级的学生占全校学生总数的____________;
(6)九年级的女生数是全校女生数的____________.
0
10
20
30
40
50
60
70
80
90
50
70
55
65
40
75
80
60
六年级
七年级
八年级
九年级
女生
男生
【难度】★★
【答案】(1); (2);(3);(4);(5);(6).
【解析】全校男生人数为70+65+75+60=270;全校女生人数为:50+55+40+80=225;
总人数:270+225=495.
(1) ; (2) ; (3) ;
(4); (5) ; (6) .
【总结】考查一个数的几分之几是多少以及一个数比另一个数多(少)几分之几的运用.
(1)写出分子分母的积是81的所有最简分数;
(2)写出分子分母之和是20的所有最简分数.
【难度】★★
【答案】(1) ; (2) .
【解析】最简分数:分子、分母只有公因数1的分数.
【总结】考查最简分数的意义.
除以a的与的差,所得的商是,求数a,并把a在数轴上表示出来.
【难度】★★
8509006731000
【答案】,
【解析】,解得:.
【总结】考查分数的列式计算.
将化成循环小数,小数点右边第1234位的数字是______.
【难度】★★★
【答案】1.
【解析】,.
【总结】考查对循环小数的理解.
一项工程,甲独做18天完成,乙独做15天完成,甲、乙两人合作,但甲途中有事,请假4天,那么完成任务时,甲实际做了几天?
【难度】★★★
【答案】6.
【解析】;.
【总结】考查工程问题中三个量之间的关系,需注意的是此过程中乙一直在工作.
计算:
(1);
(2);
(3);
(4).
【难度】★★★
【答案】(1) ;(2) ;(3) ;(4) .
【解析】(1)原式==;
(2)原式==7-=;
(3) 原式=;
(4) 原式=1+2+3+4+5+=15+=.
【总结】考查分数的巧算,注意运算方法的掌握及运用.
计算:.
【难度】★★★
【答案】.
【解析】原式=
=.
【总结】考查复杂分式的巧算方法.
我们规定:符号“”表示选择两个数中较大数的运算,例如:,
符号“”表示选择两个数中较小数的运算,例如:.
试计算(结果保留分数):(1);(2).
【难度】★★★
【答案】(1);(2).
【解析】(1)原式==;
(2)原式==.
【总结】考查新题型的理解以及两个数比较大小的方法,若a、b、m均为正整数,且a 则有.
A、B、C、D、E为不同整数.
(1)A、B为两位数,A < B,,A =______,B =______;
(2)A < B < C < D < E,,A =______,B =______,C =______, D=______,E =______.
【难度】★★★
【答案】(1) A =10, B =15;(2) A =16, B =27,C =36,D=48, E =54.
【解析】(1)==+=+;
(2)==+=+=(+)+(+)=(+)+(++).
【总结】考查分数的性质及计算.
给定以下数列:,,,,,,,,,,,,,,,,……,按此规律完成以下填空:
(1)是第______个分数;
(2)第200个分数是______(几分之几);
(3)前400个分数的和与前200个分数的和之差是______.
【难度】★★★
【答案】(1)111;(2) ;(3) .
【解析】(1) 按分母分组,每组分别有1,3,5,7个数,共有:1+3+5+…+(2n-1)=个数.那
么第10组时,共有个数,所以是第100+11=111个分数;
(2) 第14组时,共有个数,所以第200个分数是;
(3) ,所以前400个分数的和为,
前200个分数的和为,
所以.
【总结】本题的综合性较强,主要考查找规律及数的求和,要认真观察每一项的特征.
公元前500年左右,古希腊的毕达哥拉斯学派就开始用数学方法研究音乐.他们发现:弹拨琴弦,发出的声音的声调高低,取决于弦的长度.绷得一样紧的几根弦,如果长度的比能够表示成整数比,那么发出的音就比较和谐.如果三根弦的长度之比是15 : 12 : 10,把它们绷得一样紧,并用同样的力弹拨,它们将分别发出很调和的乐声do、mi、so.研究15、12、10的倒数发现,,我们称15、12、10为一组调和数.
填空,使下列三数为从小到大的一组调和数(无需写过程及证明)
(1)3,______,6;
(2)k + 1,2k + 1,______;(其中,k为正整数);
(3)______,n,______(其中,n为大于2的偶数)(答案用含n的式子表示,只需 写出一组符合条件的数即可)
【难度】★★★
【答案】(1) 4;(2) ;(3) n-2,.
【解析】(1) ;(2);
(3)举例计算,如n-2为第一个数.
【总结】考查新题型的理解,本题为理解调和数之间的关系.
课后作业
判断题:
1、两个素数相加的和一定是偶数.( )
2、个位上是3、6、9的自然数一定能被3整除.( )
3、若,则a = 25,b = 49.( )
4、真分数的倒数是假分数.( )
5、对于正整数a、b、m,若满足b > a,则一定有.( )
6、如果A比B多,那么B比A少.( ).
【难度】★
【答案】×××√√√.
【解析】反例:1、2+3=5;2、13;3、a = 50,b = 98.
【总结】考查数的整除和分数的一些相关概念的理解.
如果(a、b、c都是正整数),那么a、c的最大公因数是______.
【难度】★
【答案】c
【解析】c是a的因数,也是c的最大因数.
【总结】考查数的整除和公因数的概念.
【作业3】 一个分数的分子与分母的和是12,满足条件的最简分数有______.
【难度】★★
【答案】;;; .
【解析】最简分数:分子、分母只有公因数1的分数.
【总结】考查最简分数的意义.
【作业4】两桶同样重量的油,第一桶用去了它的,第二桶用去了吨,比较两桶中剩余的油量,发现一样重,则原来两桶油各重______吨.
【难度】★★
【答案】1.
【解析】依题意有用去的油也一样多,.
【总结】考查已知一个数的几分之几是多少,求这个数.
有一个六位数,x是大于0而小于10的自然数,y为0,一定能同时被2、5、3整除的数是( )
A. B. C. D.
【难度】★★
【答案】B
【解析】能同时被2、5整除的数,末位数一定是0,再考虑能被3整除的条件.
【总结】考查同时被2、5、3整除的数.
下列说法正确的个数是( )
甲用6天时间完成了某项工作,那么他每天完成这项工作的;
和相等的分数有无数多个;
大于小于的最简分数只有一个;
分子和分母都是偶数的分数一定不是最简分数;
分子和分母都是素数的分数一定是最简分数.
A、1个 B、2个 C、3个 D、4个
【难度】★★
【答案】C
【解析】②④⑤正确
【总结】考查分数的意义和最简分数的的概念.
用______去除62、74、110余数均为2.
【难度】★★★
【答案】12.
【解析】根据题意,即求60、72、108的最大公因数.
【总结】本题主要考查最大公因数的运用,注意区分“除”和“除以”的区别.
已知m、n是正整数,且m + n = 28,如果,那么______.
【难度】★★★
【答案】12.
【解析】由得,可知2n也是某数的平方,且为偶数,
所以2n可能为4、16、36,即n可能为2、8、18,m可能为10、20、30,
又题中m + n = 28,所以n=8,m=20.
【总结】考查数的平方的意义和2n表示偶数.
计算:
(1);
(2).
【难度】★★★
【答案】(1) ;(2).
【解析】(1) 原式=
=204+
=;
(2) 原式=
= .
【总结】本题主要考查分数巧算的方法.
甲乙两人在400米的环形跑道上练习跑步,跑完一圈,甲需要5分钟,乙需要3分20秒.
(1)如果甲乙两人同时同地朝同方向跑步,那么他们各跑几圈后能在原出发点再次相遇?
(2)若丙在甲、乙某次相遇时也加入了他们开始同方向跑步,且丙的速度是70米每分钟,问过多长时间后三人再次相遇?
【难度】★★★
【答案】(1) 甲跑2圈,乙3圈;(2)40分钟后.
【解析】(1) 由于乙带有小数,故转化为秒,甲300秒,乙200秒,最小公倍数为600秒,甲跑2圈,乙3圈.
(2) 丙跑一圈40/7分钟,甲5分钟,乙10/3分钟,先去分母,三数分别乘以21,计算最小公倍数,结果再除以21即可.[120,105,70]=840,故需要840/21=40分钟,甲跑8圈,乙12圈,丙7圈.
【总结】本题是一道应用题,综合性较强,主要考查最小公倍数的运用,解题时注意认真分
析.
内容分析
本讲将通过讲解易错点和常考题型帮助同学们做好期中复习.
知识结构
1209675215900
模块一:数的整除
知识精讲
基本内容
注意点
1.1 整数和整除的意义
1、整数与自然数的概念;
2、整除与除尽的联系与区别.
1.2 因数和倍数
1、因数(约数)与倍数的概念;
2、因数(约数)与倍数的求法.
1.3 能被2,5整除的数
1、能被2或5整除的数的特征;
2、能同时被2和5整除的数的特征;
3、*能被3或9整除的数的特征;
4、*奇数与偶数运算性质.
1.4 素数、合数和分解素因数
1、素数(质数)与合数的概念及判断;
2、100以内的素数;
3、短除法分解素因数.
1.5 公因数和最大公因数
1、公因数、最大公因数和互素的概念;
2、求两个数的最大公因数;
3、*求三个数的最大公因数;
4、最大公因数的应用.
1.6 公倍数与最小公倍数
1、公倍数和最小公倍数的概念;
2、求两个数的最小公倍数;
3、*求三个数的最小公倍数;
4、最小公倍数的应用.
例题解析
概念辨析判断:
(1)最大的正整数和最大的负整数都不存在.( )
(2)a除以b,如果除得的商是整数且余数为零,我们就说a能被b整除.( )
(3)任何正整数都能被0整除.( )
(4),则n一定能整除m.( )
(5)能同时被6,8整除的数一定能被48整除.( )
(6)一个正整数至少有两个因数.( )
(7)一个正整数的倍数一定能被它的因数整除.( )
(8)奇数的因数一定是奇数.( )
(9)两个正整数的和或差的奇偶性相同.( )
(10)两个偶数的积是偶数,两个偶数的商也是偶数.( )
(11)两个素数的和一定是偶数.( )
(12)两个连续素数的乘积一定是奇数.( )
(13)两个连续正整数的和一定是素数.( )
(14)一个合数至少有三个因数.( )
(15)最小的自然数,最小的质数,最小的合数的和是7.( )
(16)两个不同的素数一定互素.( )
(17)如果两个整数的公因数是1,则这两个数一定互素.( )
(18)7能整除a,又是b的最小倍数,所以a和b的最大公因数是7.( )
(19)正整数a、b,若,那么a、b的最大公因数是4.( )
(20)36和48的公因数共有6个.( )
(21)两个正整数的最大公因数一定能整除这两个数.( )
(22)若(a、b、c都是正整数),则a与b的最大公因数是c.( )
(23)若,则两个正整数m、n的最小公倍数是m.( )
(24)几个正整数的最大公因数一定比它们的最小公倍数小.( )
(25)若三个正整数只有公因数1,则这三个数两两互素.( ).
【难度】★
【答案】××××√ √√√√× ×××√× √√√×√ √××√×
【解析】整除的意义、因数和倍数、分解素因数等相关知识点的理解和应用.
【总结】考查数的整除中相关概念的理解和辨析.
写出50以内的所有素数_______________________________.
【难度】★
【答案】2,3,5,7,11,13,17,19,23,29,31,37,41,43,47.
【解析】素数的因数只有1和它本身.
【总结】考查素数的概念.
能整除24的数有________________.
【难度】★
【答案】1,2,3,4,6,8,12,24.
【解析】本题即求24的因数有哪些.
【总结】考查整除的意义.
在1~100这100个整数中,有25个素数,则合数有______个.
【难度】★
【答案】74.
【解析】.
【总结】注意“1”既不是素数也不是合数.
将342分解素因数为________________________________.
【难度】★
【答案】.
【解析】分解素因数是将一个合数分解成几个素数乘积的形式,注意书写格式.
【总结】本题主要考查分解素因数的概念.
,则m的因数有______个.
【难度】★★
【答案】16.
【解析】法一:,120的因数有16个;
法二:,则m的因数有个.
【总结】考查求一个数的因数有多少的方法.
既是160的因数,又能被2整除的正整数有______个.
【难度】★★
【答案】10.
【解析】160的因数有12个,除了1和5不能被2整除,其它均可.
【总结】考查因数和整除的概念.
从0、1、2、5四个数字中选三个数字组成的数字不重复的三位数,其中,偶数有______个,能被5整除的数有______个,能被5整除的偶数有______个.
【难度】★★
【答案】10;10;6.
【解析】从0、1、2、5四个数字中选三个数字组成的数字不重复的三位数一共有18个,列举即可.
【总结】考查偶数、能被5整除的数的特征.
已知这个数,在内填上一个数字,若要使这个数能被3整除,应填_______________,若要使这个数能被9整除,应填________________.
【难度】★★
【答案】1或4或7; 4.
【解析】2+5+7+9=23,要使这个数能被3整除,则23+的数的和是3的倍数;要使这个
数能被9整除,则23+的数的和是9的倍数.
【总结】考查能被3、9整除的数的特征.
150和125共有的素因数是______________.
【难度】★★
【答案】5,5.
【解析】;125=.
【总结】考查求两个数共有的素因数的方法,注意重复的素因数也要全部写出.
求下列各组数的最大公因数和最小公倍数.
(1)187和442; (2)36、84和39.
【难度】★★
【答案】(1) 17,4862;(2)3,3276.
【解析】(1) ;
所以最大公因数17; 最小公倍数.
(2).
所以最大公因数3; 最小公倍数.
【总结】考查求两个(三个)数的最大公因数和最小公倍数的方法.
先填空,再找规律:
(1)15和6的最大公因数是______,最小公倍数是______,15和6的积是______,它们的最大公因数和最小公倍数的积是______.
(2)从上面的题目中,你发现了什么规律?
(3)根据你发现的规律填空:
甲、乙两数的最大公因数是3,最小公倍数是90,若甲数是18,则乙数是______.
【难度】★★
【答案】(1) 3,30,90, 90;
(2) 两数的最大公因数和最小公倍数的乘积等于这两数的积.
(3) 15.
【解析】(1) ;(2)找规律;(3) .
【总结】考查两数的最大公因数、最小公倍数与两数乘积的关系.
有铅笔433支,橡皮260块,平均分给若干学生,学生数在30~50之间,最后剩余铅笔13支、橡皮8块,问学生究竟有多少人?
【难度】★★★
【答案】42.
【解析】 .
学生数在30~50之间的公因数为42.
【总结】考查在限定条件下求公因数.
黄老师在学校的暖棚里培育花苗,她先每隔20厘米挖一个洞,准备载入花苗,当挖好31个洞时,觉得花苗之间间隔大小,于是决定改为每隔30厘米栽一个花苗。那么有多少个洞需要填埋好?
【难度】★★★
【答案】20.
【解析】20和30的最小公倍数是60,已经挖好的总长度为cm;
不需要填平的洞为:,所以需要填埋好的洞为:个.
【总结】考查种树问题,树的棵数=间隔数+1.
一个正整数被4除余3,被6除余5,被9除余8,则这个数最小是多少?
【难度】★★★
【答案】35.
【解析】4、6、9的最小公倍数是36,则这个数为35.
【总结】考查对最小公倍数的理解.
公共汽车总站有三条线路,第一条每8分钟发一辆车,第二条每10分钟发一辆车,第三条每16分钟发一辆车,早上6:00三条路线同时发出第一辆车,该总站发出最后一辆车是20:00,求该总站最后一次三辆车同时发出的时刻.
【难度】★★★
【答案】19:20.
【解析】8、10、16的最小公倍数是80,6:00—20:00共14小时,
分钟,20:00的前40分钟即为19:20.
【总结】考查发车间隔问题,关键是求出每一次同时发车的周期.
模块二:分数
知识精讲
基本内容
注意点
2.1 分数与除法
1、分数的概念和意义;
2、分数与除法的关系.
2.2 分数的基本性质
1、基本性质;
2、最简分数的概念与约分.
2.3 分数的大小比较
1、公分母与分数的通分;
2、分数比较大小的基本方法;
3、*分数比较大小的特殊方法.
2.4 分数的加减法
1、分数加减法的计算法则;
2、真分数、假分数、带分数的概念及运算;
3、分数加减法的应用.
2.5 分数的乘法
1、分数乘法的计算法则;
2、分数乘法的应用.
2.6 分数的除法
1、分数除法的计算法则;
2、倒数的概念;
3、分数除法的应用.
2.7 分数与小数互化
1、分数化为小数的方法;
2、可化为有限小数的分数的特征;
3、有限小数化为分数的方法;
4、循环小数的相关概念;
5、*循环小数化为分数的技巧.
2.8 分数小数的四则混合运算
1、分数小数混合运算时互化的原则;
2、常见的分数与小数的互化;
3、*速算与巧算.
2.9 分数运算的应用
1、一个数是另一个数的几分之几;
2、一个数的几分之几是多少;
3、已知一个数的几分之几,求这个数;
4、一个数比另一个数多(或)少几分之几;
5、*工程问题.
例题解析
概念辨析判断:
(1)如果a、b是正整数,则;( )
(2)因为,所以除法就是分数;( )
(3)把一个蛋糕分给10个小朋友,则每人能获得这个蛋糕的;( )
(4)分子、分母都是正整数,且由奇数和偶数组成的分数是最简分数;( )
(5)若a、b、n都是正整数,则;( )
(6)分数的分子分母同时加上或减去一个不为零的相同的数,分数的大小一定改变;( )
(7)约分就是将一个分数的分子与分母的最大公因数约去的过程;( )
(8)约分后是,约分后可得;( )
(9)若是真分数,而是假分数,则正整m = 6;( )
(10)任何一个正整数,除以一个真分数,所得的数一定比原数大;( )
(11)任何一个正整数,乘以一个假分数,所得的数一定比原数大;( )
(12)若,则a和b互为倒数;( )
(13)除以一个数的倒数,等于乘以这个数;( )
(14)1.5的与500的相等;( )
(15)一袋面粉,第一天用去,第二天用去,此时还剩下千克;( )
(16)甲数比乙数多,则乙数比甲数少.( )
【难度】★
【答案】××××× ×√××√ ×√√√× √
【解析】分数与除法的关系,分数的几分之几的意义等.
【总结】考查对分数基本概念性质等理解.
写出下列各图形中阴影部分是整体的几分之几.
41910089535
______; ______; ______.
【难度】★
【答案】.
【解析】利用图形的割补即得.
【总结】考查对分数意义的理解.
一本80页的书,小红第一天读26页,第二天读32页,未读的页数是总页数的______.
【难度】★
【答案】.
【解析】.
【总结】考查一个数是另一个数的几分之几.
.
【难度】★
【答案】18,42,42.
【解析】分数的分子和分母同时乘以一个不为0的数,分数的值不变.
【总结】考查分数和除法的关系,分数的基本性质.
分数中的a和b同时缩小为原来的,得到的分数是原来的( )
A. B. C.3倍 D.9倍
【难度】★
【答案】A.
【解析】.
【总结】考查分数的性质.
下列说法中正确的有( )个
(1)最简分数的分子和分母没有公因数;
(2)一个分数,分子扩大到原来的4倍,分母缩小到原来的一半,此分数就扩大2倍;
(3)分数就是两个正整数相除的商;
(4)做同一个零件,王师傅3小时做22个,李师傅4小时35分钟做33个,张师傅90分钟做13个,则张师傅的效率最高.
A.0 B.1 C.2 D.3
【难度】★★
【答案】B
【解析】(1) 有公因数1;(2) 此分数就扩大8倍;(3) 表述不对. 应为:两个正整数相除
的商可以用分数表示.(4) 正确
【总结】考查分数中的相关概念的理解.
6
A
B
C
1
2
3
4
5
0
(1)指出数轴上A、B、C各点分别表示什么数?
A:______;B:______;C:______.
(2)用数轴上的点表示分数和.
1
2
3
4
5
0
6
【难度】★★
【答案】(1) A:______;B:______;C:__3____.
5143503810(2)
【解析】分数在数轴上的表示如图.
【总结】考查分数在数轴上的表示.
分数的值小于1且分母是100的最简分数有______个.
【难度】★★
【答案】40.
【解析】当分子小于100,且个位数是1、3、7、9时符合题意.共有个.
【总结】考查最简分数的意义.
,括号中能填的正整数有______个.
【难度】★★
【答案】51.
【解析】原式可化为: ;.
【总结】考查分数的性质.
比较大小:______,______,______.
【难度】★★
【答案】>、<、>.
【解析】(1) 分子相同,分母大的反而小;
(2) ;
(3)
【总结】考查比较分数大小.
在分数、、、中能化为有限小数的是____________.
【难度】★★
【答案】、.
【解析】当一个分数化成最简分数后,若分母的因数中只有2和5,则这个分数可化为有限小数.
【总结】考查分数能化为有限小数的条件.
下列正确的有( )个
;;;.
A.1 B.2 C.3 D.4
【难度】★★
【答案】B
【解析】①④正确.
【总结】考查分数的性质.
计算:
(1)(结果化为假分数);
(2)(结果化为带分数);
(3);
(4);
(5);
(6).
【难度】★★
【答案】(1) ;(2) ;(3) ;(4) ;(5);(6).
【解析】(1) 原式=;
(2) 原式=;
(3) 原式=;
(4) ;
(5) 原式===;
(6) 原式==.
【总结】考查分数的混合运算,注意运算法则的准确运用,能巧算时要巧算.
某初级中学男女生人数情况如图,看图回答:(填几分之几)
(1)全校男生人数是全校学生数的____________;
(2)全校女生人数是全校男生人数的____________;
(3)八年级女生人数比八年级男生人数少____________;
(4)七年级男生人数比七年级女生人数多____________;
(5)六年级的学生占全校学生总数的____________;
(6)九年级的女生数是全校女生数的____________.
0
10
20
30
40
50
60
70
80
90
50
70
55
65
40
75
80
60
六年级
七年级
八年级
九年级
女生
男生
【难度】★★
【答案】(1); (2);(3);(4);(5);(6).
【解析】全校男生人数为70+65+75+60=270;全校女生人数为:50+55+40+80=225;
总人数:270+225=495.
(1) ; (2) ; (3) ;
(4); (5) ; (6) .
【总结】考查一个数的几分之几是多少以及一个数比另一个数多(少)几分之几的运用.
(1)写出分子分母的积是81的所有最简分数;
(2)写出分子分母之和是20的所有最简分数.
【难度】★★
【答案】(1) ; (2) .
【解析】最简分数:分子、分母只有公因数1的分数.
【总结】考查最简分数的意义.
除以a的与的差,所得的商是,求数a,并把a在数轴上表示出来.
【难度】★★
8509006731000
【答案】,
【解析】,解得:.
【总结】考查分数的列式计算.
将化成循环小数,小数点右边第1234位的数字是______.
【难度】★★★
【答案】1.
【解析】,.
【总结】考查对循环小数的理解.
一项工程,甲独做18天完成,乙独做15天完成,甲、乙两人合作,但甲途中有事,请假4天,那么完成任务时,甲实际做了几天?
【难度】★★★
【答案】6.
【解析】;.
【总结】考查工程问题中三个量之间的关系,需注意的是此过程中乙一直在工作.
计算:
(1);
(2);
(3);
(4).
【难度】★★★
【答案】(1) ;(2) ;(3) ;(4) .
【解析】(1)原式==;
(2)原式==7-=;
(3) 原式=;
(4) 原式=1+2+3+4+5+=15+=.
【总结】考查分数的巧算,注意运算方法的掌握及运用.
计算:.
【难度】★★★
【答案】.
【解析】原式=
=.
【总结】考查复杂分式的巧算方法.
我们规定:符号“”表示选择两个数中较大数的运算,例如:,
符号“”表示选择两个数中较小数的运算,例如:.
试计算(结果保留分数):(1);(2).
【难度】★★★
【答案】(1);(2).
【解析】(1)原式==;
(2)原式==.
【总结】考查新题型的理解以及两个数比较大小的方法,若a、b、m均为正整数,且a
A、B、C、D、E为不同整数.
(1)A、B为两位数,A < B,,A =______,B =______;
(2)A < B < C < D < E,,A =______,B =______,C =______, D=______,E =______.
【难度】★★★
【答案】(1) A =10, B =15;(2) A =16, B =27,C =36,D=48, E =54.
【解析】(1)==+=+;
(2)==+=+=(+)+(+)=(+)+(++).
【总结】考查分数的性质及计算.
给定以下数列:,,,,,,,,,,,,,,,,……,按此规律完成以下填空:
(1)是第______个分数;
(2)第200个分数是______(几分之几);
(3)前400个分数的和与前200个分数的和之差是______.
【难度】★★★
【答案】(1)111;(2) ;(3) .
【解析】(1) 按分母分组,每组分别有1,3,5,7个数,共有:1+3+5+…+(2n-1)=个数.那
么第10组时,共有个数,所以是第100+11=111个分数;
(2) 第14组时,共有个数,所以第200个分数是;
(3) ,所以前400个分数的和为,
前200个分数的和为,
所以.
【总结】本题的综合性较强,主要考查找规律及数的求和,要认真观察每一项的特征.
公元前500年左右,古希腊的毕达哥拉斯学派就开始用数学方法研究音乐.他们发现:弹拨琴弦,发出的声音的声调高低,取决于弦的长度.绷得一样紧的几根弦,如果长度的比能够表示成整数比,那么发出的音就比较和谐.如果三根弦的长度之比是15 : 12 : 10,把它们绷得一样紧,并用同样的力弹拨,它们将分别发出很调和的乐声do、mi、so.研究15、12、10的倒数发现,,我们称15、12、10为一组调和数.
填空,使下列三数为从小到大的一组调和数(无需写过程及证明)
(1)3,______,6;
(2)k + 1,2k + 1,______;(其中,k为正整数);
(3)______,n,______(其中,n为大于2的偶数)(答案用含n的式子表示,只需 写出一组符合条件的数即可)
【难度】★★★
【答案】(1) 4;(2) ;(3) n-2,.
【解析】(1) ;(2);
(3)举例计算,如n-2为第一个数.
【总结】考查新题型的理解,本题为理解调和数之间的关系.
课后作业
判断题:
1、两个素数相加的和一定是偶数.( )
2、个位上是3、6、9的自然数一定能被3整除.( )
3、若,则a = 25,b = 49.( )
4、真分数的倒数是假分数.( )
5、对于正整数a、b、m,若满足b > a,则一定有.( )
6、如果A比B多,那么B比A少.( ).
【难度】★
【答案】×××√√√.
【解析】反例:1、2+3=5;2、13;3、a = 50,b = 98.
【总结】考查数的整除和分数的一些相关概念的理解.
如果(a、b、c都是正整数),那么a、c的最大公因数是______.
【难度】★
【答案】c
【解析】c是a的因数,也是c的最大因数.
【总结】考查数的整除和公因数的概念.
【作业3】 一个分数的分子与分母的和是12,满足条件的最简分数有______.
【难度】★★
【答案】;;; .
【解析】最简分数:分子、分母只有公因数1的分数.
【总结】考查最简分数的意义.
【作业4】两桶同样重量的油,第一桶用去了它的,第二桶用去了吨,比较两桶中剩余的油量,发现一样重,则原来两桶油各重______吨.
【难度】★★
【答案】1.
【解析】依题意有用去的油也一样多,.
【总结】考查已知一个数的几分之几是多少,求这个数.
有一个六位数,x是大于0而小于10的自然数,y为0,一定能同时被2、5、3整除的数是( )
A. B. C. D.
【难度】★★
【答案】B
【解析】能同时被2、5整除的数,末位数一定是0,再考虑能被3整除的条件.
【总结】考查同时被2、5、3整除的数.
下列说法正确的个数是( )
甲用6天时间完成了某项工作,那么他每天完成这项工作的;
和相等的分数有无数多个;
大于小于的最简分数只有一个;
分子和分母都是偶数的分数一定不是最简分数;
分子和分母都是素数的分数一定是最简分数.
A、1个 B、2个 C、3个 D、4个
【难度】★★
【答案】C
【解析】②④⑤正确
【总结】考查分数的意义和最简分数的的概念.
用______去除62、74、110余数均为2.
【难度】★★★
【答案】12.
【解析】根据题意,即求60、72、108的最大公因数.
【总结】本题主要考查最大公因数的运用,注意区分“除”和“除以”的区别.
已知m、n是正整数,且m + n = 28,如果,那么______.
【难度】★★★
【答案】12.
【解析】由得,可知2n也是某数的平方,且为偶数,
所以2n可能为4、16、36,即n可能为2、8、18,m可能为10、20、30,
又题中m + n = 28,所以n=8,m=20.
【总结】考查数的平方的意义和2n表示偶数.
计算:
(1);
(2).
【难度】★★★
【答案】(1) ;(2).
【解析】(1) 原式=
=204+
=;
(2) 原式=
= .
【总结】本题主要考查分数巧算的方法.
甲乙两人在400米的环形跑道上练习跑步,跑完一圈,甲需要5分钟,乙需要3分20秒.
(1)如果甲乙两人同时同地朝同方向跑步,那么他们各跑几圈后能在原出发点再次相遇?
(2)若丙在甲、乙某次相遇时也加入了他们开始同方向跑步,且丙的速度是70米每分钟,问过多长时间后三人再次相遇?
【难度】★★★
【答案】(1) 甲跑2圈,乙3圈;(2)40分钟后.
【解析】(1) 由于乙带有小数,故转化为秒,甲300秒,乙200秒,最小公倍数为600秒,甲跑2圈,乙3圈.
(2) 丙跑一圈40/7分钟,甲5分钟,乙10/3分钟,先去分母,三数分别乘以21,计算最小公倍数,结果再除以21即可.[120,105,70]=840,故需要840/21=40分钟,甲跑8圈,乙12圈,丙7圈.
【总结】本题是一道应用题,综合性较强,主要考查最小公倍数的运用,解题时注意认真分
析.
同课章节目录
