高中物理人教版选修3.4 作业题 第十二章 机械波 综合测试题 Word版含解析
文档属性
| 名称 | 高中物理人教版选修3.4 作业题 第十二章 机械波 综合测试题 Word版含解析 |

|
|
| 格式 | DOC | ||
| 文件大小 | 306.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-12 14:41:11 | ||
图片预览



文档简介
第十二章 《机械波》综合测试
时间:90分钟 满分:100分
一、选择题(1~6为单选,7~10为多选,每小题4分,共40分)
1.雷声隆隆不绝,这是一种什么现象( B )
A.声音的共鸣现象
B.声波在云层界面上发生多次反射的现象
C.声波绕过障碍物的衍射现象
D.声波在叠加时的干涉现象
2.一列简谐波在均匀介质中沿直线向右以v的速度传播,图中上半部分所示的各质点的平衡位置在同一直线上,间距相等,以质点1从平衡位置开始竖直向上运动为起始时刻,经过时间t,前13个质点第一次形成如图下半部分所示波形图,则两质点平衡位置的间距d为( D )
A. B. C. D.
解析:由题意可知,各质点的起振方向竖直向上,前13个质点第一次形成如题图下半部分所示波形图说明波已经传播了2 T,即2 T=t;而该波的波长λ=v T;由图象可知:λ=8d;联立以上各式得:d=,故D正确.
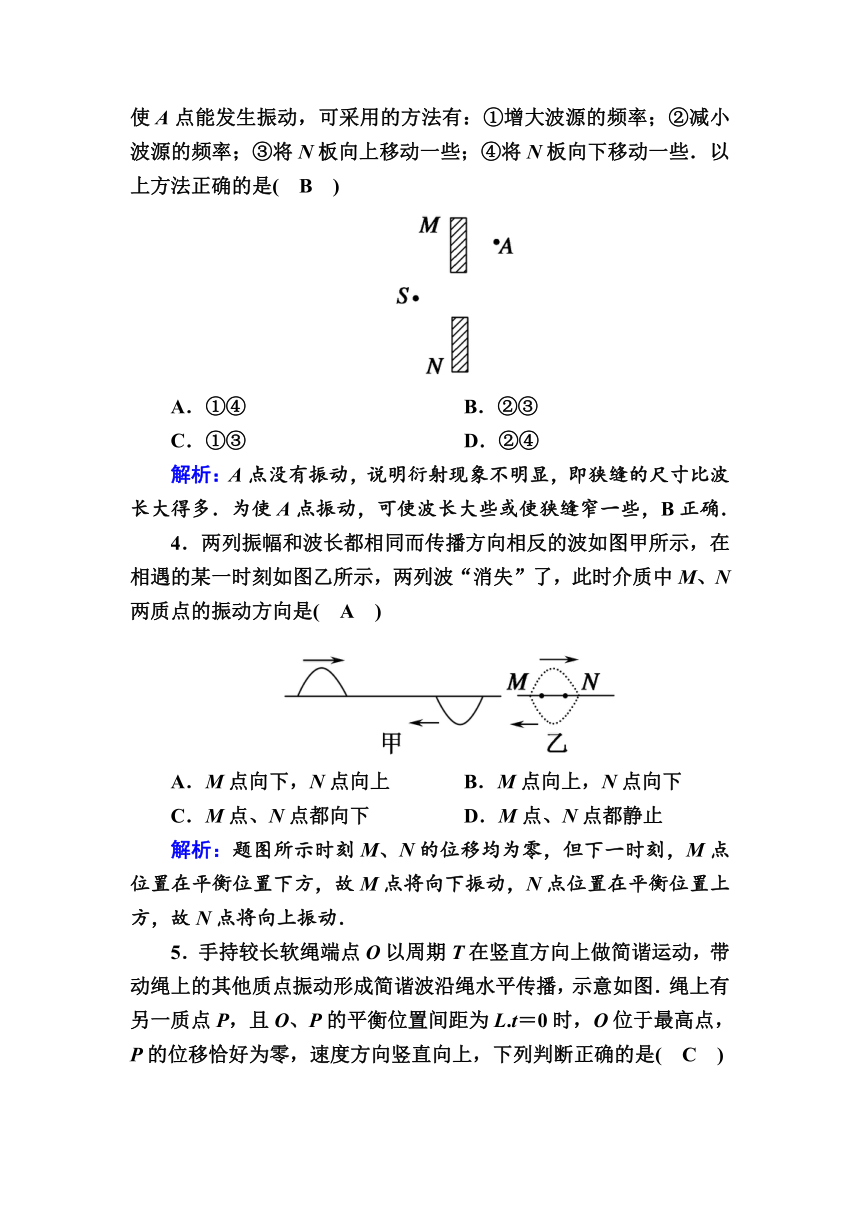
3.如图所示,S为波源,M、N为两块挡板,其中M板固定,N板可上下移动,两板中间有一狭缝,此时测得A点没有振动,为了使A点能发生振动,可采用的方法有:①增大波源的频率;②减小波源的频率;③将N板向上移动一些;④将N板向下移动一些.以上方法正确的是( B )
A.①④ B.②③
C.①③ D.②④
解析:A点没有振动,说明衍射现象不明显,即狭缝的尺寸比波长大得多.为使A点振动,可使波长大些或使狭缝窄一些,B正确.
4.两列振幅和波长都相同而传播方向相反的波如图甲所示,在相遇的某一时刻如图乙所示,两列波“消失”了,此时介质中M、N两质点的振动方向是( A )
A.M点向下,N点向上 B.M点向上,N点向下
C.M点、N点都向下 D.M点、N点都静止
解析:题图所示时刻M、N的位移均为零,但下一时刻,M点位置在平衡位置下方,故M点将向下振动,N点位置在平衡位置上方,故N点将向上振动.
5.手持较长软绳端点O以周期T在竖直方向上做简谐运动,带动绳上的其他质点振动形成简谐波沿绳水平传播,示意如图.绳上有另一质点P,且O、P的平衡位置间距为L.t=0时,O位于最高点,P的位移恰好为零,速度方向竖直向上,下列判断正确的是( C )
A.该简谐波是纵波
B.该简谐波的最大波长为2L
C.t=时,P在平衡位置上方
D.t=时,P的速度方向竖直向上
解析:振动方向与传播方向垂直,故该简谐波是横波,A错误;根据“下坡上”判断,P距离O的最近距离L=λ,所以最大波长等于4L,B错误;经过T,P位于波峰,所以T时,P在平衡位置上方,C正确;在T时,P正在从波峰回到平衡位置,速度方向竖直向下,D错误.
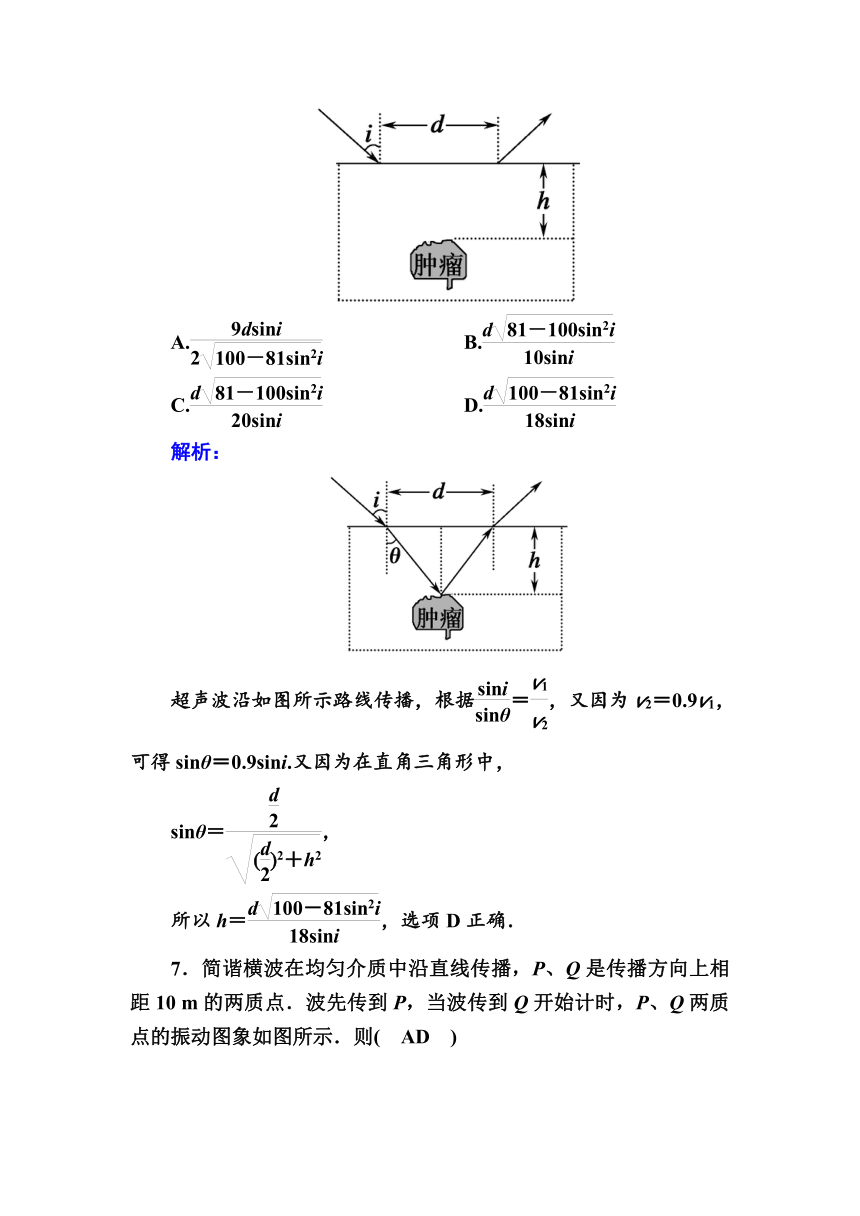
6.“B超”可用于探测人体内脏的病变状况.下图是超声波从肝脏表面入射,经折射与反射,最后从肝脏表面射出的示意图.超声波在进入肝脏发生折射时遵循的规律与光的折射规律类似,可表述为=(式中θ1是入射角,θ2是折射角,v1、v2分别是超声波在肝外和肝内的传播速度),超声波在肿瘤表面发生反射时遵循的规律与光的反射规律相同.已知v2=0.9v1,入射点与出射点之间的距离是d,入射角是i,肿瘤的反射面恰好与肝脏表面平行,则肿瘤离肝脏表面的深度h为( D )
A. B.
C. D.
解析:
超声波沿如图所示路线传播,根据=,又因为v2=0.9v1,可得sinθ=0.9sini.又因为在直角三角形中,
sinθ=,
所以h=,选项D正确.
7.简谐横波在均匀介质中沿直线传播,P、Q是传播方向上相距10 m的两质点.波先传到P,当波传到Q开始计时,P、Q两质点的振动图象如图所示.则( AD )
A.质点Q开始振动的方向沿y轴正方向
B.该波从P传到Q的时间可能为7 s
C.该波的传播速度可能为2 m/s
D.该波的波长可能为6 m
解析:由图可知,t=0时质点Q处于平衡位置,t=时运动至波峰,故其起振方向沿y轴正方向,A正确;仍由图可知,T=6 s,质点Q比质点P到达同一振动状态晚了Δt=nT+T=(6n+4) s(n=0,1,2…),此即为该波从P传到Q所需的时间,当Δt=7 s时n=,故B错误,由v== m/s知,当v=2 m/s时n=,故C错误;再由λ=vT= m知,当n=1时λ=6 m,故D正确.
8.陈明、张磊和杜丽三位同学,在学习了波的干涉的知识后,通过以下的实验,开展了一次研究性学习活动.他们将收录机外接两只较小的单扬声器音箱,两只音箱并排放置,彼此相距0.5~1 m,播放事先录好的频率为2~3 kHz的磁带.然后在两扬声器连线相距3~6 m的平行线上向一个方向上运动,的确听到了忽高忽低的声音.假如两列声波的波谷在P点相遇,则下述正确的是( BD )
A.质点P的振动始终是减弱的
B.质点P的振幅最大
C.质点P的位移始终最小
D.质点P的位移有时为零
解析:两列波的波谷在P点相遇,振动方向相同,振动应加强,故B、D正确.
9.如图所示,为一横波发生器的显示屏,可以显示出波由O点从左向右传播的图象,屏上每一小格长度为1 cm.在t=0时刻横波发生器上能显示的波形如图所示,因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5 s时,观察者看到C处恰好第三次(从C开始振动后算起)出现在平衡位置,则该波的波速可能是( BCD )
A.3.6 cm/s B.4.8 cm/s
C.6 cm/s D.7.2 cm/s
解析:由题图读出波长λ=12 cm,若图示时刻波刚好传到A点,波传到质点C的时间为1.5T,质点C再经过1.5T恰好第三次出现在平衡位置,则t=5 s=1.5T+1.5T,得T= s,波速v==7.2 cm/s;若图示时刻波刚好传到x=12 cm处,波传到质点C的时间为T,质点C再经过1.5T恰好第三次出现在平衡位置,则t=5 s=1.5T+T,得T=2 s,波速v==6 cm/s;若图示时刻波刚好传到B点,波传到质点C的时间为0.5T,质点C再经过1.5T恰好第三次出现在平衡位置,则t=5 s=1.5T+0.5T,得T=2.5 s,波速v==4.8 cm/s.所以B、C、D正确,A错误.
10.坐标原点O处有一波源S,在xOy坐标平面内发出沿y轴方向振动的平面简谐横波,波在沿x轴方向的均匀介质中传播的速度为v=200 m/s,已知t=0时刻,沿x轴正方向传播的一列波刚好到达x=40 m处,如图所示.下列说法中正确的是( AC )
A.波源S开始振动的方向沿y轴负方向
B.在x轴上x=40 m处的质点在t=0.05 s时位移最大
C.若波源沿着x轴正方向匀速靠近位于坐标为(100 m,0)处的接收器(图中未画出),则接收器接收到的频率比波源振动频率高
D.若波源沿着x轴正方向匀速运动,同时,位于坐标为(100 m,0)处的接收器(图中未画出)向x轴负方向匀速运动,则接收器接收到的频率不断变小
解析:本题考查的知识点主要是波动问题中波的图象与波速公式和多普勒效应,其中将波动问题的计算与多普勒效应结合在一起,是命题的一种新的尝试.因为波向右传播,则可认为左侧的O点为波源,根据后面的质点要重复前面的质点的振动且波形不被破坏,可判断出波源是向下即沿y轴负方向开始振动的,A正确;由图知λ=20 m,由T== s=0.1 s,因t=,所以质点向下振动到最大振幅处又回到了平衡位置,故B错误;当波源靠近接收器时,在单位时间接收到的信号的个数增多,即接收到的频率增大,C、D都是波源与接收器相对靠近,故C正确,D错误.正确选项为A、C.
二、填空题(每小题9分,共18分)
11.弹性绳沿x轴放置,左端位于坐标原点,用手握住绳的左端,当t=0时使其开始沿y轴做振幅为8 cm的简谐运动,在t=0.25 s时,绳上形成如图所示的波形,则该波的波速为20 cm/s;在t=2.75 s时,位于x2=45 cm处的质点N恰好第一次沿y轴正方向通过平衡位置.
解析:由图象可知,A=8 cm,T=4t=1 s,λ=20 cm,所以波速v== cm/s=20 cm/s.由波的传播方向可以判断,t=0.25 s时,x1=5 cm处的质点正向下运动,所以N点开始振动时也是沿y轴负方向.波传到N点所用的时间为t1== s=2.25 s,质点N第一次沿y轴正向通过平衡位置时t=t1+=2.75 s.
12.如图(a),在xy平面内有两个沿z方向做简谐振动的点波源S1(0,4)和S2(0,-2).两波源的振动图线分别如图(b)和图(c)所示.两列波的波速均为1.00 m/s.两列波从波源传播到点A(8,-2)的路程差为2 m,两列波引起的点B(4,1)处质点的振动相互减弱(填“加强”或“减弱”),点C(0,0.5)处质点的振动相互加强(填“加强”或“减弱”).
解析:点波源S1(0,4)的振动形式传播到点A(8,-2)的路程为L1=10 m,点波源S2(0,-2)的振动形式传播到点A(8,-2)的路程为L2=8 m,两列波从波源传播到点A(8,-2)的路程差为ΔL=L1-L2=2 m.由于两列波的波源到点B(4,1)的路程相等,路程差为零,且t=0时两列波的波源的振动方向相反,所以两列波到达点B时振动方向相反,引起的点B处质点的振动相互减弱;由振动图线可知,波动周期为T=2 s,波长λ=vT=2 m.由于两列波的波源到点C(0,0.5)的路程分别为3.5 m和2.5 m,路程差为1 m,而t=0时两列波的波源的振动方向相反,所以两列波到达点C时振动方向相同,引起的点C处质点的振动相互加强.
三、计算题(共42分)
13.(10分)取一根柔软的弹性绳,将绳的右端固定在竖直墙壁上,绳的左端自由,使绳处于水平伸直状态,从绳的端点开始用彩笔每隔0.50 m标记一个点,依次记为A、B、C、D……如图所示.现用振动装置拉着绳子的端点A沿竖直方向做简谐运动,若A点起振方向向上,经0.1 s第一次达正向最大位移,此时C点恰好开始起振,则
(1)绳子形成的波是横波还是纵波?简要说明判断依据,并求波速为多大;
(2)从A开始振动,经多长时间J点第一次向下达到最大位移?
(3)画出当J点第一次向下达到最大位移时的波形.
答案:(1)横波 质点振动方向与波的传播方向垂直 10 m/s
(2)0.75 s (3)见解析
解析:(1)绳子形成的波是横波,因为质点振动方向与波的传播方向垂直.由题意知,波的周期T=0.4 s,故长为λ=4 m,所以波速v==10 m/s.
(2)从A开始振动,设J点开始起振经过时间t1,则t1===0.45 s,设J点向上起振后经t2时间第一次到负向最大位移,则t2=T=0.3 s,所以t=t1+t2=0.75 s.
(3)波形如图所示.
14.(10分)某实验室中悬挂着一弹簧振子A和一单摆B,弹簧振子的弹簧和小球(球中间有孔)都套在固定的光滑竖直杆上.某次有感地震中观察到静止的振子A开始振动4.0 s后,单摆B才开始摆动.此次地震中同一震源产生的地震纵波和横波的波长分别为10 km和5.0 km,频率为1.0 Hz.假设该实验室恰好位于震源的正上方,求震源离实验室的距离.
答案:40 km
解析:设地震纵波和横波的传播速度分别为vP和vS,则vP=fλP,vS=fλS,式中,f为地震波的频率,λP和λS分别表示地震纵波和横波的波长.设震源离实验室的距离为s,纵波从震源传播到实验室所需时间为t,则s=vPt,s=vS(t+Δt),式中,Δt为摆B开始摆动的时刻与振子A开始振动的时刻之差.由以上各式得s=,代入数据得s=40 km.
15.(10分)一列简谐横波在介质中沿x轴正向传播,波长不小于10 cm.O和A是介质中平衡位置分别位于x=0和x=5 cm处的两个质点.t=0时开始观测,此时质点O的位移为y=4 cm,质点A处于波峰位置;t= s时,质点O第一次回到平衡位置,t=1 s时,质点A第一次回到平衡位置.求:
(1)简谐波的周期、波速和波长;
(2)质点O的位移随时间变化的关系式.
答案:(1)4 s 7.5 cm/s 30 cm
(2)y=0.08cos(+)或y=0.08sin(+)
解析:(1)设振动周期为T.由于质点A在0到1 s内由最大位移处第一次回到平衡位置,经历的是个周期,由此可知T=4 s①
由于质点O与A的距离5 cm小于半个波长,且波沿x轴正向传播,O在t= s时回到平衡位置,而A在t=1 s时回到平衡位置,时间相差 s.两质点平衡位置的距离除以传播时间,可得波的速度
v=7.5 cm/s②
利用波长、波速和周期的关系得,简谐波的波长λ=30 cm③
(2)设质点O的位移随时间变化的关系为y=Acos④
将①式及题给条件代入上式得⑤
解得φ0=,A=8 cm⑥
质点O的位移随时间变化的关系式为
y=0.08cos(国际单位制)⑦
或y=0.08sin(国际单位制)
16.(12分)有两列简谐横波a、b在同一介质中沿x轴正方向传播,波速均为v=2.5 m/s.在t=0时,两列波的波峰正好在x=2.5 m处重合,如图所示.
(1)求两列波的周期Ta和Tb.
(2)求t=0时,两列波的波峰重合处的所有位置.
(3)辨析题:分析并判断在t=0时是否存在两列波的波谷重合处.
某同学分析如下:既然两列波的波峰存在重合处,那么波谷与波谷重合处也一定存在.只要找到这两列波半波长的最小公倍数,即可得到波谷与波谷重合处的所有位置.
你认为该同学的分析正确吗?若正确,求出这些点的位置.
若不正确,指出错误处并通过计算说明理由.
答案:(1)1 s 1.6 s (2)x=(2.5±20k) m,k=0,1,2,3…
(3)见解析
解析:(1)从图中可以看出两列波的波长分别为λa=2.5 m,λb=4.0 m,因此它们的周期分别为
Ta== s=1 s,Tb== s=1.6 s.
(2)两列波波长的最小公倍数为S=20 m,t=0时,两列波的波峰重合处的所有位置为x=(2.5±20k) m,k=0,1,2,3,…
(3)该同学的分析不正确.要找两列波的波谷与波谷重合处,必须从波峰重合处出发,找到这两列波半波长的奇数倍恰好相等的位置.设距离x=2.5 m的L处两列波的波谷与波谷相遇,并设
L=(2m-1),L=(2n-1),式中m、n均为正整数.
只要找到相应的m、n即可.
将λa=2.5 m,λb=4.0 m代入并整理,得
===.
由于上式中,m、n在整数范围内无解,所以不存在波谷与波谷重合处.
时间:90分钟 满分:100分
一、选择题(1~6为单选,7~10为多选,每小题4分,共40分)
1.雷声隆隆不绝,这是一种什么现象( B )
A.声音的共鸣现象
B.声波在云层界面上发生多次反射的现象
C.声波绕过障碍物的衍射现象
D.声波在叠加时的干涉现象
2.一列简谐波在均匀介质中沿直线向右以v的速度传播,图中上半部分所示的各质点的平衡位置在同一直线上,间距相等,以质点1从平衡位置开始竖直向上运动为起始时刻,经过时间t,前13个质点第一次形成如图下半部分所示波形图,则两质点平衡位置的间距d为( D )
A. B. C. D.
解析:由题意可知,各质点的起振方向竖直向上,前13个质点第一次形成如题图下半部分所示波形图说明波已经传播了2 T,即2 T=t;而该波的波长λ=v T;由图象可知:λ=8d;联立以上各式得:d=,故D正确.
3.如图所示,S为波源,M、N为两块挡板,其中M板固定,N板可上下移动,两板中间有一狭缝,此时测得A点没有振动,为了使A点能发生振动,可采用的方法有:①增大波源的频率;②减小波源的频率;③将N板向上移动一些;④将N板向下移动一些.以上方法正确的是( B )
A.①④ B.②③
C.①③ D.②④
解析:A点没有振动,说明衍射现象不明显,即狭缝的尺寸比波长大得多.为使A点振动,可使波长大些或使狭缝窄一些,B正确.
4.两列振幅和波长都相同而传播方向相反的波如图甲所示,在相遇的某一时刻如图乙所示,两列波“消失”了,此时介质中M、N两质点的振动方向是( A )
A.M点向下,N点向上 B.M点向上,N点向下
C.M点、N点都向下 D.M点、N点都静止
解析:题图所示时刻M、N的位移均为零,但下一时刻,M点位置在平衡位置下方,故M点将向下振动,N点位置在平衡位置上方,故N点将向上振动.
5.手持较长软绳端点O以周期T在竖直方向上做简谐运动,带动绳上的其他质点振动形成简谐波沿绳水平传播,示意如图.绳上有另一质点P,且O、P的平衡位置间距为L.t=0时,O位于最高点,P的位移恰好为零,速度方向竖直向上,下列判断正确的是( C )
A.该简谐波是纵波
B.该简谐波的最大波长为2L
C.t=时,P在平衡位置上方
D.t=时,P的速度方向竖直向上
解析:振动方向与传播方向垂直,故该简谐波是横波,A错误;根据“下坡上”判断,P距离O的最近距离L=λ,所以最大波长等于4L,B错误;经过T,P位于波峰,所以T时,P在平衡位置上方,C正确;在T时,P正在从波峰回到平衡位置,速度方向竖直向下,D错误.
6.“B超”可用于探测人体内脏的病变状况.下图是超声波从肝脏表面入射,经折射与反射,最后从肝脏表面射出的示意图.超声波在进入肝脏发生折射时遵循的规律与光的折射规律类似,可表述为=(式中θ1是入射角,θ2是折射角,v1、v2分别是超声波在肝外和肝内的传播速度),超声波在肿瘤表面发生反射时遵循的规律与光的反射规律相同.已知v2=0.9v1,入射点与出射点之间的距离是d,入射角是i,肿瘤的反射面恰好与肝脏表面平行,则肿瘤离肝脏表面的深度h为( D )
A. B.
C. D.
解析:
超声波沿如图所示路线传播,根据=,又因为v2=0.9v1,可得sinθ=0.9sini.又因为在直角三角形中,
sinθ=,
所以h=,选项D正确.
7.简谐横波在均匀介质中沿直线传播,P、Q是传播方向上相距10 m的两质点.波先传到P,当波传到Q开始计时,P、Q两质点的振动图象如图所示.则( AD )
A.质点Q开始振动的方向沿y轴正方向
B.该波从P传到Q的时间可能为7 s
C.该波的传播速度可能为2 m/s
D.该波的波长可能为6 m
解析:由图可知,t=0时质点Q处于平衡位置,t=时运动至波峰,故其起振方向沿y轴正方向,A正确;仍由图可知,T=6 s,质点Q比质点P到达同一振动状态晚了Δt=nT+T=(6n+4) s(n=0,1,2…),此即为该波从P传到Q所需的时间,当Δt=7 s时n=,故B错误,由v== m/s知,当v=2 m/s时n=,故C错误;再由λ=vT= m知,当n=1时λ=6 m,故D正确.
8.陈明、张磊和杜丽三位同学,在学习了波的干涉的知识后,通过以下的实验,开展了一次研究性学习活动.他们将收录机外接两只较小的单扬声器音箱,两只音箱并排放置,彼此相距0.5~1 m,播放事先录好的频率为2~3 kHz的磁带.然后在两扬声器连线相距3~6 m的平行线上向一个方向上运动,的确听到了忽高忽低的声音.假如两列声波的波谷在P点相遇,则下述正确的是( BD )
A.质点P的振动始终是减弱的
B.质点P的振幅最大
C.质点P的位移始终最小
D.质点P的位移有时为零
解析:两列波的波谷在P点相遇,振动方向相同,振动应加强,故B、D正确.
9.如图所示,为一横波发生器的显示屏,可以显示出波由O点从左向右传播的图象,屏上每一小格长度为1 cm.在t=0时刻横波发生器上能显示的波形如图所示,因为显示屏的局部故障,造成从水平位置A到B之间(不包括A、B两处)的波形无法被观察到(故障不影响波在发生器内传播).此后的时间内,观察者看到波形相继传经B、C处,在t=5 s时,观察者看到C处恰好第三次(从C开始振动后算起)出现在平衡位置,则该波的波速可能是( BCD )
A.3.6 cm/s B.4.8 cm/s
C.6 cm/s D.7.2 cm/s
解析:由题图读出波长λ=12 cm,若图示时刻波刚好传到A点,波传到质点C的时间为1.5T,质点C再经过1.5T恰好第三次出现在平衡位置,则t=5 s=1.5T+1.5T,得T= s,波速v==7.2 cm/s;若图示时刻波刚好传到x=12 cm处,波传到质点C的时间为T,质点C再经过1.5T恰好第三次出现在平衡位置,则t=5 s=1.5T+T,得T=2 s,波速v==6 cm/s;若图示时刻波刚好传到B点,波传到质点C的时间为0.5T,质点C再经过1.5T恰好第三次出现在平衡位置,则t=5 s=1.5T+0.5T,得T=2.5 s,波速v==4.8 cm/s.所以B、C、D正确,A错误.
10.坐标原点O处有一波源S,在xOy坐标平面内发出沿y轴方向振动的平面简谐横波,波在沿x轴方向的均匀介质中传播的速度为v=200 m/s,已知t=0时刻,沿x轴正方向传播的一列波刚好到达x=40 m处,如图所示.下列说法中正确的是( AC )
A.波源S开始振动的方向沿y轴负方向
B.在x轴上x=40 m处的质点在t=0.05 s时位移最大
C.若波源沿着x轴正方向匀速靠近位于坐标为(100 m,0)处的接收器(图中未画出),则接收器接收到的频率比波源振动频率高
D.若波源沿着x轴正方向匀速运动,同时,位于坐标为(100 m,0)处的接收器(图中未画出)向x轴负方向匀速运动,则接收器接收到的频率不断变小
解析:本题考查的知识点主要是波动问题中波的图象与波速公式和多普勒效应,其中将波动问题的计算与多普勒效应结合在一起,是命题的一种新的尝试.因为波向右传播,则可认为左侧的O点为波源,根据后面的质点要重复前面的质点的振动且波形不被破坏,可判断出波源是向下即沿y轴负方向开始振动的,A正确;由图知λ=20 m,由T== s=0.1 s,因t=,所以质点向下振动到最大振幅处又回到了平衡位置,故B错误;当波源靠近接收器时,在单位时间接收到的信号的个数增多,即接收到的频率增大,C、D都是波源与接收器相对靠近,故C正确,D错误.正确选项为A、C.
二、填空题(每小题9分,共18分)
11.弹性绳沿x轴放置,左端位于坐标原点,用手握住绳的左端,当t=0时使其开始沿y轴做振幅为8 cm的简谐运动,在t=0.25 s时,绳上形成如图所示的波形,则该波的波速为20 cm/s;在t=2.75 s时,位于x2=45 cm处的质点N恰好第一次沿y轴正方向通过平衡位置.
解析:由图象可知,A=8 cm,T=4t=1 s,λ=20 cm,所以波速v== cm/s=20 cm/s.由波的传播方向可以判断,t=0.25 s时,x1=5 cm处的质点正向下运动,所以N点开始振动时也是沿y轴负方向.波传到N点所用的时间为t1== s=2.25 s,质点N第一次沿y轴正向通过平衡位置时t=t1+=2.75 s.
12.如图(a),在xy平面内有两个沿z方向做简谐振动的点波源S1(0,4)和S2(0,-2).两波源的振动图线分别如图(b)和图(c)所示.两列波的波速均为1.00 m/s.两列波从波源传播到点A(8,-2)的路程差为2 m,两列波引起的点B(4,1)处质点的振动相互减弱(填“加强”或“减弱”),点C(0,0.5)处质点的振动相互加强(填“加强”或“减弱”).
解析:点波源S1(0,4)的振动形式传播到点A(8,-2)的路程为L1=10 m,点波源S2(0,-2)的振动形式传播到点A(8,-2)的路程为L2=8 m,两列波从波源传播到点A(8,-2)的路程差为ΔL=L1-L2=2 m.由于两列波的波源到点B(4,1)的路程相等,路程差为零,且t=0时两列波的波源的振动方向相反,所以两列波到达点B时振动方向相反,引起的点B处质点的振动相互减弱;由振动图线可知,波动周期为T=2 s,波长λ=vT=2 m.由于两列波的波源到点C(0,0.5)的路程分别为3.5 m和2.5 m,路程差为1 m,而t=0时两列波的波源的振动方向相反,所以两列波到达点C时振动方向相同,引起的点C处质点的振动相互加强.
三、计算题(共42分)
13.(10分)取一根柔软的弹性绳,将绳的右端固定在竖直墙壁上,绳的左端自由,使绳处于水平伸直状态,从绳的端点开始用彩笔每隔0.50 m标记一个点,依次记为A、B、C、D……如图所示.现用振动装置拉着绳子的端点A沿竖直方向做简谐运动,若A点起振方向向上,经0.1 s第一次达正向最大位移,此时C点恰好开始起振,则
(1)绳子形成的波是横波还是纵波?简要说明判断依据,并求波速为多大;
(2)从A开始振动,经多长时间J点第一次向下达到最大位移?
(3)画出当J点第一次向下达到最大位移时的波形.
答案:(1)横波 质点振动方向与波的传播方向垂直 10 m/s
(2)0.75 s (3)见解析
解析:(1)绳子形成的波是横波,因为质点振动方向与波的传播方向垂直.由题意知,波的周期T=0.4 s,故长为λ=4 m,所以波速v==10 m/s.
(2)从A开始振动,设J点开始起振经过时间t1,则t1===0.45 s,设J点向上起振后经t2时间第一次到负向最大位移,则t2=T=0.3 s,所以t=t1+t2=0.75 s.
(3)波形如图所示.
14.(10分)某实验室中悬挂着一弹簧振子A和一单摆B,弹簧振子的弹簧和小球(球中间有孔)都套在固定的光滑竖直杆上.某次有感地震中观察到静止的振子A开始振动4.0 s后,单摆B才开始摆动.此次地震中同一震源产生的地震纵波和横波的波长分别为10 km和5.0 km,频率为1.0 Hz.假设该实验室恰好位于震源的正上方,求震源离实验室的距离.
答案:40 km
解析:设地震纵波和横波的传播速度分别为vP和vS,则vP=fλP,vS=fλS,式中,f为地震波的频率,λP和λS分别表示地震纵波和横波的波长.设震源离实验室的距离为s,纵波从震源传播到实验室所需时间为t,则s=vPt,s=vS(t+Δt),式中,Δt为摆B开始摆动的时刻与振子A开始振动的时刻之差.由以上各式得s=,代入数据得s=40 km.
15.(10分)一列简谐横波在介质中沿x轴正向传播,波长不小于10 cm.O和A是介质中平衡位置分别位于x=0和x=5 cm处的两个质点.t=0时开始观测,此时质点O的位移为y=4 cm,质点A处于波峰位置;t= s时,质点O第一次回到平衡位置,t=1 s时,质点A第一次回到平衡位置.求:
(1)简谐波的周期、波速和波长;
(2)质点O的位移随时间变化的关系式.
答案:(1)4 s 7.5 cm/s 30 cm
(2)y=0.08cos(+)或y=0.08sin(+)
解析:(1)设振动周期为T.由于质点A在0到1 s内由最大位移处第一次回到平衡位置,经历的是个周期,由此可知T=4 s①
由于质点O与A的距离5 cm小于半个波长,且波沿x轴正向传播,O在t= s时回到平衡位置,而A在t=1 s时回到平衡位置,时间相差 s.两质点平衡位置的距离除以传播时间,可得波的速度
v=7.5 cm/s②
利用波长、波速和周期的关系得,简谐波的波长λ=30 cm③
(2)设质点O的位移随时间变化的关系为y=Acos④
将①式及题给条件代入上式得⑤
解得φ0=,A=8 cm⑥
质点O的位移随时间变化的关系式为
y=0.08cos(国际单位制)⑦
或y=0.08sin(国际单位制)
16.(12分)有两列简谐横波a、b在同一介质中沿x轴正方向传播,波速均为v=2.5 m/s.在t=0时,两列波的波峰正好在x=2.5 m处重合,如图所示.
(1)求两列波的周期Ta和Tb.
(2)求t=0时,两列波的波峰重合处的所有位置.
(3)辨析题:分析并判断在t=0时是否存在两列波的波谷重合处.
某同学分析如下:既然两列波的波峰存在重合处,那么波谷与波谷重合处也一定存在.只要找到这两列波半波长的最小公倍数,即可得到波谷与波谷重合处的所有位置.
你认为该同学的分析正确吗?若正确,求出这些点的位置.
若不正确,指出错误处并通过计算说明理由.
答案:(1)1 s 1.6 s (2)x=(2.5±20k) m,k=0,1,2,3…
(3)见解析
解析:(1)从图中可以看出两列波的波长分别为λa=2.5 m,λb=4.0 m,因此它们的周期分别为
Ta== s=1 s,Tb== s=1.6 s.
(2)两列波波长的最小公倍数为S=20 m,t=0时,两列波的波峰重合处的所有位置为x=(2.5±20k) m,k=0,1,2,3,…
(3)该同学的分析不正确.要找两列波的波谷与波谷重合处,必须从波峰重合处出发,找到这两列波半波长的奇数倍恰好相等的位置.设距离x=2.5 m的L处两列波的波谷与波谷相遇,并设
L=(2m-1),L=(2n-1),式中m、n均为正整数.
只要找到相应的m、n即可.
将λa=2.5 m,λb=4.0 m代入并整理,得
===.
由于上式中,m、n在整数范围内无解,所以不存在波谷与波谷重合处.
