浙教版九年级科学上册 3.4机械效率专题(课件 19张ppt)
文档属性
| 名称 | 浙教版九年级科学上册 3.4机械效率专题(课件 19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2020-10-13 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
3.4
机械效率专题
在实际生活中,我们很难实现W额外=0,
一般用W有用、W总的比值来衡量能量的利用率,
也就是机械效率(Mechanical
efficiency)
η=
×
100%
=
W有用
W总
(2)有用功总小于总功,所以机械效率总小于1
(1)机械效率一般用百分数表示,没有单位
(3)η越大,表示机械工作时能量的利用率越高
W有用
W有用
+
W额外
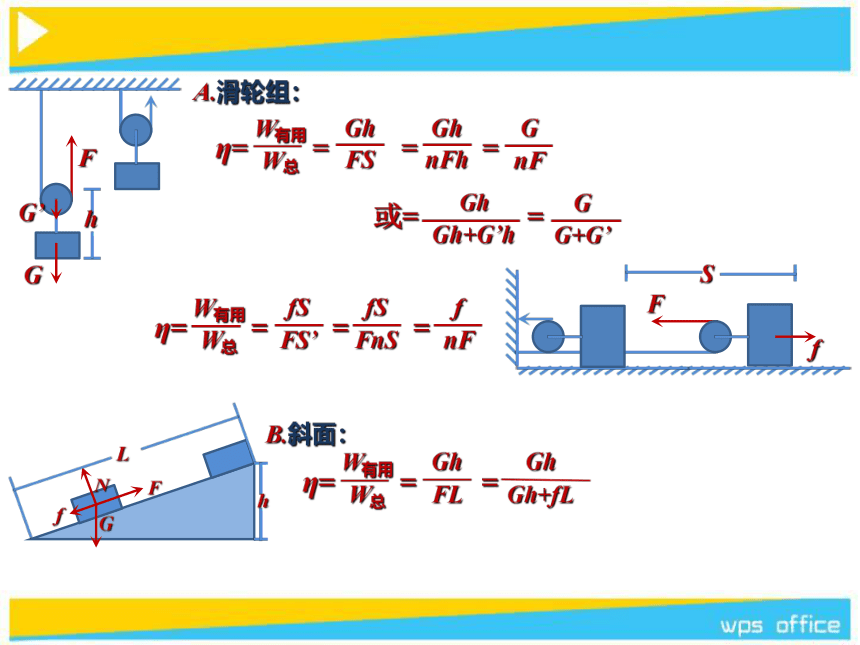
A.滑轮组:
F
G
G’
h
W有用
W总
η=
=
=
=
fS
FS’
fS
FnS
f
nF
F
f
S
F
f
N
G
h
L
B.斜面:
W有用
W总
η=
=
=
Gh
FL
Gh
Gh+fL
W有用
W总
η=
=
=
=
或=
=
Gh
FS
Gh
nFh
Gh
Gh+G’h
G
G+G’
G
nF
η
=
G
G+G’
在滑轮组中有:
如何增大机械效率
举例:如何增大滑轮组的机械效率?
(1)对同一个滑轮组而言,G’是固定的。所提物重G越大,机械效率就越大。
结论:
η
=
=
=
1
-
G
G+G’
G+G’-G’
G+G’
G’
G+G’
(1)若所提物重G不变,G’越小,机械效率越大。
也就是说,一般可以通过减小机械自重和增加物体重力来增大机械效率
例1
实验课上,甲、乙两个小组所组装的滑轮组如图所示,已知所用滑轮、绳子的规格完全相同,不计绳重及摩擦,则下列说法中正确的是(
)
A.甲较省力,甲的机械效率较大
B.乙较省力,两种方式机械效率一样大
C.乙机械效率较大,两种方式提升物体的最大质量相等
D.以相同速度提升等质量的物体,甲功率大
解析
直接根据
,得到η甲
=
η乙;排除A、C;
再根据
,得到F甲
:
F乙
=
3
:
2;故B正确
最后因为S
=
nh,v物相等时,
v甲
:
v乙
=
2
:
3;
所以P甲
:
P乙
=
F甲
v甲
:
F乙
v乙
=1;故D错
η
=
G
G+G’
F
=
G+G’
n
练习
甲乙两个滑轮组如图所示,其中的每一个滑轮都相同,用它们分别将重物G1、G2提高相同的高度,不计滑轮组的摩擦,下列说法中正确的是(
)
A.若G1=G2,拉力做的额外功相同
B.若G1=G2,拉力做的总功相同
C.若G1=G2,甲的机械效率大于乙的机械效率
D.用甲乙一种任何一个滑轮组提起不同的重物,机械效率不变
C
例2
如图所示,人以600N的力向下拉动绕在滑轮组的绳子一端
10s,使绳端向下移动了1.5m,重物匀速上升了0.5m,已知滑轮组的机械效率70%(g=10N/kg)。
(1)按题意画出滑轮组的绕绳;
(2)人所做功的功率多大;
(3)被吊起重物质量多大;
解析
(1)
∵
S=nh,∴n=S/h=1.5m/0.5m=3,根据“奇动偶定”
应从动滑轮出发绕线,如图所示:
(2)P=W/t=FS/t=600N×1.5m/10s=90w
;
(3)η=
,
整理得:G×0.5m=0.7×600N×1.5m,
得G=1260N,m=126kg
;
Gh
FS
练习
如图所示,用滑轮组来匀速拉动地面上的小车,请画出最省力的绕线方式。若地面与小车间的摩擦力为f,人拉绳子的拉力为F,试写出η的表达式(忽略其他阻力)
答案
绕线如图所示:
fS
4FS
η=
=
f
4F
例3
如图所示,将重为100N的物体匀速从斜面的底端拉至顶端。已知斜面长5m,高2m,拉力F=50N。求该装置的机械效率。
解析
如图装置结合了斜面和动滑轮,没有现成公式可以利用。因此我们应从η的定义式着手,找到对应的W有用、W总;
η=
=
=
=
=40%
Gh
FS
W有用
W总
100N×2m
2×50N×5m
Gh
2FL
该题中F通过的距离S应是物体移动距离的2倍,即S=2L
练习
一斜面的机械效率为80%,应用它可以用100N的力,匀速地沿斜面拉起重400N的物体,则斜面的高与长度之比为多少?
η=
=
80%
Gh
FL
=
80%
400N×h
100N×L
=
h
L
1
5
例4
如图是一个两面光滑的斜面,β>α,同一个物体分别在AC和BC斜面受拉力匀速运动到C点,所需拉力分别为FA、FB,所做功分别是WA、WB,则
(
)
A.FA=FB,WA=WB
B.FAC.FAD.FA>FB,WA>WB
解析
光滑斜面η
=100%,即FL=Gh,故WA=WB
;
又有LA>LB,所以FAB正确
例4
一个重为500N的物体,用拉力F使它沿着长5m,高3m的光滑斜面AB,由A匀速拉上平台B,在这过程中拉力做功
J,若在平台BC上使物体前进5m,这时重力做功
J,若实际推力为350N,则斜面的机械效率为
。
答案
FL=Gh=500N×3m=1500J;WG=0;
η=
=
=
85.7%
Gh
FL
1500J
1750J
物体的内能
扩散、热运动、内能
扩散—物质分子从高浓度区域向低浓
度区域转移,直到均匀分布的现象。
注意:固体之间亦可发生扩散,如接触面光滑的金块和铅块
久置后会相互粘连
扩散的本质
热运动—大量粒子的无规则运动
通过观察分析,我们发现:
(1)温度越高,粒子热运动越剧烈,扩散快,内能就大
(2)质量越大,做热运动的粒子数目越多,内能越大
内能—物体内部大量做热运动的粒子所具有的能量
红墨水的扩散
内能的普遍性
我们已经知道内能的微观本质是粒子的热运动,那么
当粒子停止运动时,物体的内能也就消失了
但是粒子停止运动是需要条件的,只有当物体温度
达到-273.15
℃时,粒子才能静止;而这一温度只在理
论上存在可能,在实际情况下只能接近而已。
因此我们可以说:所有的物体均具有
能内,如0
℃的冰,其分子仍在较小的范
围内无规则振动,因而也具有内能;我们
只能说1kg
20
℃的水的内能相较1kg
0
℃
的冰内能更大。
内能的比较
(1)所有的物体均具有内能,我们只能比较物体内能的大小,不能说物体没有内能
(2)对于一定质量的物体,温度越高,物体的内能就越大
(3)对于一定温度的物体,质量越大,物体的内能就越大
改变内能的途径
实验
实验现象
结论
1
2
3
气体冲开胶塞,瓶内出现白雾
容器壁变热,乙醚气体冲开胶塞
温度升高,浸有燃料的棉花燃烧
气体对外做功,温度降低,内能减小
对乙醚做功,温度升高,内能增大
对气体做功,温度升高,内能增大
1.
做功
我们发现:物体对外做功,自身内能减小;
对物体做功,
物体内能增加。
2.
热传递
将冰块放在50℃的水中,冰块吸热熔化,水温也有所降低
这是因为,存在温度差的两个物体相互接触后,一部分热量会从高温物体传递至低温物体,直至两者的温度相等。
我们知道,对同种物质而言,决定内能大小的因素是
温度和质量,那么就存在这样的可能性:
一块0℃的冰的内能
>
一滴1℃的水的内能
若将这滴水滴在冰上,内能是如何传递的呢?
显然,这滴水会放热凝固,也就是说热传递的方向是:
水→冰
内能低→内能高
因此热量传递的方向是:
高温物体→低温物体
和物体内能的高低没有必然联系
(1)做功改变内能:实质上是其它形式的能和内能之间转化.
(2)热传递改变内能:实质上是各物体间内能的转移.
(3)做功和热传递在改变内能效果上是等效的.
做功和热传递改变内能的关系
比热
定义:1kg某物质温度升高1℃所吸收的热量
Q=cmΔt
符号为c,单位
J/(kg·℃)
热量的计算
Δt表示物体温度的改变值
Δt=t-t0(t0为初始温度,t为最终温度)
物体升温
t>t0,即Δt>0,Q为正值,物体吸热;
物体降温
t物体传递的热量用Q表示,单位为J
例
水的比热为4.2×103J/(kg·℃),将500ml水从20℃加热至50℃需多少热量
Q=cmΔt
=
4.2×103J/(kg·℃)×0.5kg×30℃
=
63000J
热值
定义:1kg某种燃料完全燃烧时放出的热量,叫做这种燃料的热值,
也叫燃烧值。
符号为q,单位
J/kg
Q=qm
燃烧放热的计算
例
液氢的热值为4.6×108J/kg,则完全燃烧5.5kg液氢能释放多少热量
Q=qm=4.6×108J/kg×5.5kg=2.53×109J
3.4
机械效率专题
在实际生活中,我们很难实现W额外=0,
一般用W有用、W总的比值来衡量能量的利用率,
也就是机械效率(Mechanical
efficiency)
η=
×
100%
=
W有用
W总
(2)有用功总小于总功,所以机械效率总小于1
(1)机械效率一般用百分数表示,没有单位
(3)η越大,表示机械工作时能量的利用率越高
W有用
W有用
+
W额外
A.滑轮组:
F
G
G’
h
W有用
W总
η=
=
=
=
fS
FS’
fS
FnS
f
nF
F
f
S
F
f
N
G
h
L
B.斜面:
W有用
W总
η=
=
=
Gh
FL
Gh
Gh+fL
W有用
W总
η=
=
=
=
或=
=
Gh
FS
Gh
nFh
Gh
Gh+G’h
G
G+G’
G
nF
η
=
G
G+G’
在滑轮组中有:
如何增大机械效率
举例:如何增大滑轮组的机械效率?
(1)对同一个滑轮组而言,G’是固定的。所提物重G越大,机械效率就越大。
结论:
η
=
=
=
1
-
G
G+G’
G+G’-G’
G+G’
G’
G+G’
(1)若所提物重G不变,G’越小,机械效率越大。
也就是说,一般可以通过减小机械自重和增加物体重力来增大机械效率
例1
实验课上,甲、乙两个小组所组装的滑轮组如图所示,已知所用滑轮、绳子的规格完全相同,不计绳重及摩擦,则下列说法中正确的是(
)
A.甲较省力,甲的机械效率较大
B.乙较省力,两种方式机械效率一样大
C.乙机械效率较大,两种方式提升物体的最大质量相等
D.以相同速度提升等质量的物体,甲功率大
解析
直接根据
,得到η甲
=
η乙;排除A、C;
再根据
,得到F甲
:
F乙
=
3
:
2;故B正确
最后因为S
=
nh,v物相等时,
v甲
:
v乙
=
2
:
3;
所以P甲
:
P乙
=
F甲
v甲
:
F乙
v乙
=1;故D错
η
=
G
G+G’
F
=
G+G’
n
练习
甲乙两个滑轮组如图所示,其中的每一个滑轮都相同,用它们分别将重物G1、G2提高相同的高度,不计滑轮组的摩擦,下列说法中正确的是(
)
A.若G1=G2,拉力做的额外功相同
B.若G1=G2,拉力做的总功相同
C.若G1=G2,甲的机械效率大于乙的机械效率
D.用甲乙一种任何一个滑轮组提起不同的重物,机械效率不变
C
例2
如图所示,人以600N的力向下拉动绕在滑轮组的绳子一端
10s,使绳端向下移动了1.5m,重物匀速上升了0.5m,已知滑轮组的机械效率70%(g=10N/kg)。
(1)按题意画出滑轮组的绕绳;
(2)人所做功的功率多大;
(3)被吊起重物质量多大;
解析
(1)
∵
S=nh,∴n=S/h=1.5m/0.5m=3,根据“奇动偶定”
应从动滑轮出发绕线,如图所示:
(2)P=W/t=FS/t=600N×1.5m/10s=90w
;
(3)η=
,
整理得:G×0.5m=0.7×600N×1.5m,
得G=1260N,m=126kg
;
Gh
FS
练习
如图所示,用滑轮组来匀速拉动地面上的小车,请画出最省力的绕线方式。若地面与小车间的摩擦力为f,人拉绳子的拉力为F,试写出η的表达式(忽略其他阻力)
答案
绕线如图所示:
fS
4FS
η=
=
f
4F
例3
如图所示,将重为100N的物体匀速从斜面的底端拉至顶端。已知斜面长5m,高2m,拉力F=50N。求该装置的机械效率。
解析
如图装置结合了斜面和动滑轮,没有现成公式可以利用。因此我们应从η的定义式着手,找到对应的W有用、W总;
η=
=
=
=
=40%
Gh
FS
W有用
W总
100N×2m
2×50N×5m
Gh
2FL
该题中F通过的距离S应是物体移动距离的2倍,即S=2L
练习
一斜面的机械效率为80%,应用它可以用100N的力,匀速地沿斜面拉起重400N的物体,则斜面的高与长度之比为多少?
η=
=
80%
Gh
FL
=
80%
400N×h
100N×L
=
h
L
1
5
例4
如图是一个两面光滑的斜面,β>α,同一个物体分别在AC和BC斜面受拉力匀速运动到C点,所需拉力分别为FA、FB,所做功分别是WA、WB,则
(
)
A.FA=FB,WA=WB
B.FA
解析
光滑斜面η
=100%,即FL=Gh,故WA=WB
;
又有LA>LB,所以FA
例4
一个重为500N的物体,用拉力F使它沿着长5m,高3m的光滑斜面AB,由A匀速拉上平台B,在这过程中拉力做功
J,若在平台BC上使物体前进5m,这时重力做功
J,若实际推力为350N,则斜面的机械效率为
。
答案
FL=Gh=500N×3m=1500J;WG=0;
η=
=
=
85.7%
Gh
FL
1500J
1750J
物体的内能
扩散、热运动、内能
扩散—物质分子从高浓度区域向低浓
度区域转移,直到均匀分布的现象。
注意:固体之间亦可发生扩散,如接触面光滑的金块和铅块
久置后会相互粘连
扩散的本质
热运动—大量粒子的无规则运动
通过观察分析,我们发现:
(1)温度越高,粒子热运动越剧烈,扩散快,内能就大
(2)质量越大,做热运动的粒子数目越多,内能越大
内能—物体内部大量做热运动的粒子所具有的能量
红墨水的扩散
内能的普遍性
我们已经知道内能的微观本质是粒子的热运动,那么
当粒子停止运动时,物体的内能也就消失了
但是粒子停止运动是需要条件的,只有当物体温度
达到-273.15
℃时,粒子才能静止;而这一温度只在理
论上存在可能,在实际情况下只能接近而已。
因此我们可以说:所有的物体均具有
能内,如0
℃的冰,其分子仍在较小的范
围内无规则振动,因而也具有内能;我们
只能说1kg
20
℃的水的内能相较1kg
0
℃
的冰内能更大。
内能的比较
(1)所有的物体均具有内能,我们只能比较物体内能的大小,不能说物体没有内能
(2)对于一定质量的物体,温度越高,物体的内能就越大
(3)对于一定温度的物体,质量越大,物体的内能就越大
改变内能的途径
实验
实验现象
结论
1
2
3
气体冲开胶塞,瓶内出现白雾
容器壁变热,乙醚气体冲开胶塞
温度升高,浸有燃料的棉花燃烧
气体对外做功,温度降低,内能减小
对乙醚做功,温度升高,内能增大
对气体做功,温度升高,内能增大
1.
做功
我们发现:物体对外做功,自身内能减小;
对物体做功,
物体内能增加。
2.
热传递
将冰块放在50℃的水中,冰块吸热熔化,水温也有所降低
这是因为,存在温度差的两个物体相互接触后,一部分热量会从高温物体传递至低温物体,直至两者的温度相等。
我们知道,对同种物质而言,决定内能大小的因素是
温度和质量,那么就存在这样的可能性:
一块0℃的冰的内能
>
一滴1℃的水的内能
若将这滴水滴在冰上,内能是如何传递的呢?
显然,这滴水会放热凝固,也就是说热传递的方向是:
水→冰
内能低→内能高
因此热量传递的方向是:
高温物体→低温物体
和物体内能的高低没有必然联系
(1)做功改变内能:实质上是其它形式的能和内能之间转化.
(2)热传递改变内能:实质上是各物体间内能的转移.
(3)做功和热传递在改变内能效果上是等效的.
做功和热传递改变内能的关系
比热
定义:1kg某物质温度升高1℃所吸收的热量
Q=cmΔt
符号为c,单位
J/(kg·℃)
热量的计算
Δt表示物体温度的改变值
Δt=t-t0(t0为初始温度,t为最终温度)
物体升温
t>t0,即Δt>0,Q为正值,物体吸热;
物体降温
t
例
水的比热为4.2×103J/(kg·℃),将500ml水从20℃加热至50℃需多少热量
Q=cmΔt
=
4.2×103J/(kg·℃)×0.5kg×30℃
=
63000J
热值
定义:1kg某种燃料完全燃烧时放出的热量,叫做这种燃料的热值,
也叫燃烧值。
符号为q,单位
J/kg
Q=qm
燃烧放热的计算
例
液氢的热值为4.6×108J/kg,则完全燃烧5.5kg液氢能释放多少热量
Q=qm=4.6×108J/kg×5.5kg=2.53×109J
同课章节目录
- 第1章 物质及其变化
- 第1节 物质的变化
- 第2节 物质的酸碱性
- 第3节 常见的酸
- 第4节 常见的碱
- 第5节 酸和碱之间发生的反应
- 第6节 几种重要的盐
- 第2章 物质转化与材料利用
- 第1节 金属材料
- 第2节 金属的化学性质
- 第3节 有机物和有机合成材料
- 第4节 物质的分类
- 第5节 物质的转化
- 第6节 材料的利用与发展
- 第3章 能量的转化与守恒
- 第1节 能量及其形式
- 第2节 机械能
- 第3节 能量转化的量度
- 第4节 简单机械
- 第5节 物体的内能
- 第6节 电能
- 第7节 核能
- 第8节 能量的转化与守恒
- 第4章 代谢与平衡
- 第1节 食物与营养
- 第2节 食物的消化与吸收
- 第3节 体内物质的运输
- 第4节 能量的获得
- 第5节 体内物质的动态平衡
- 研究性学习课题
- 一 当地酸雨情况以及对农作物和建筑物的影响
- 二 金属对社会发展的作用
- 三 寻找自行车中的杠杆
- 四 怎样防治龋齿
