2020年苏科版八年级上册第一章《全等三角形》中的运动类问题培优训练试卷(一)(Word版含答案)
文档属性
| 名称 | 2020年苏科版八年级上册第一章《全等三角形》中的运动类问题培优训练试卷(一)(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 233.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 15:47:37 | ||
图片预览


文档简介
2020八上苏科版第一章《全等三角形》中的运动类问题培优训练(一)
班级:___________姓名:___________得分:___________
一、解答题
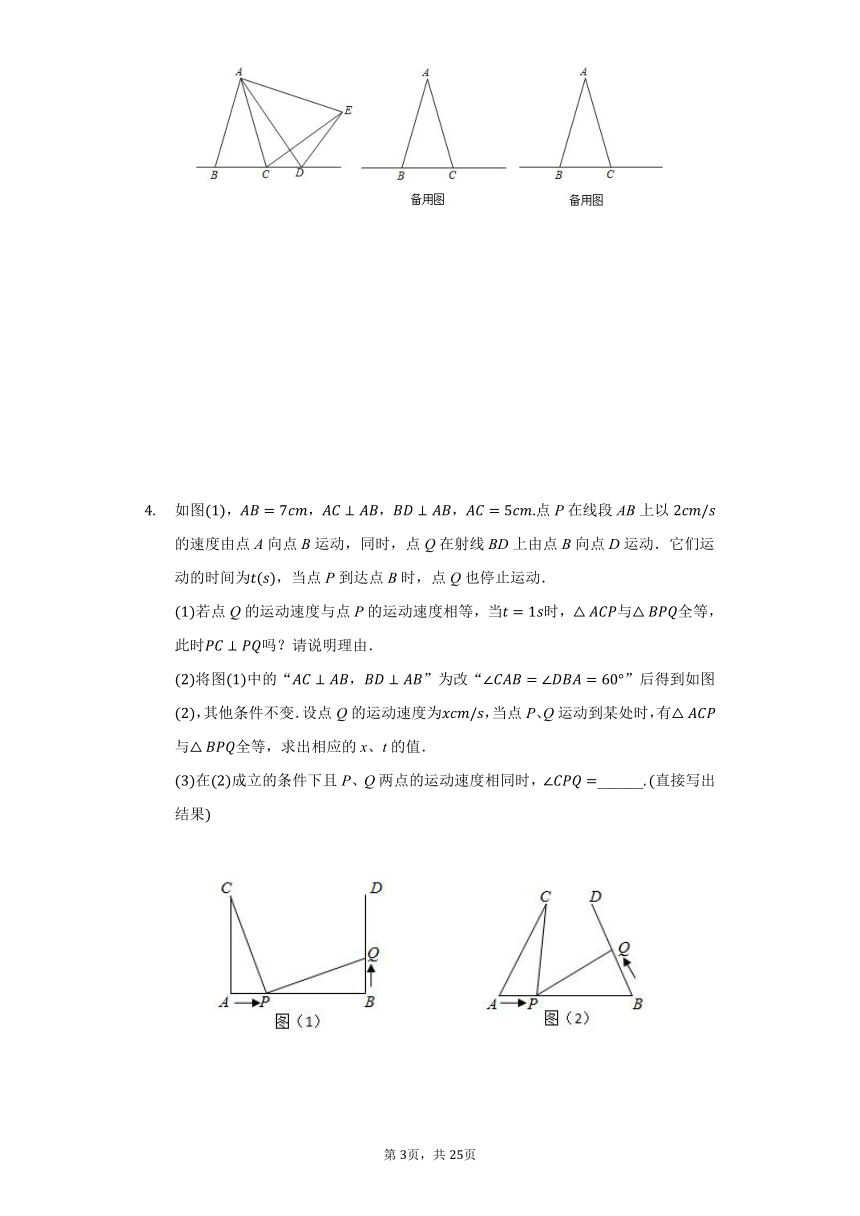
如图,在中,,,,,现有一动点P,从点A出发,沿着三角形的边运动,回到点A停止,速度为,设运动时间为ts.
如图,当______时,的面积等于面积的一半;
如图,在中,,,,在的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边运动,回到点A停止.在两点运动过程中的某一时刻,恰好≌,求点Q的运动速度.
探究:如图1和图2,四边形ABCD中,已知,,点E、F分别在BC、CD上,.
如图1,若、都是直角,把绕点A逆时针旋转至,使AB与AD重合,直接写出线段BE、DF和EF之间的数量关系______;
如图2,若、都不是直角,但满足,线段BE、DF和EF之间的结论是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由.
拓展:如图3,在中,,点D、E均在边BC边上,且,若,求DE的长.
在中,,D是直线BC上一点,以AD为一条边在AD的右侧作,使,,连接CE.
如图,当点D在BC延长线上移动时,若,则______,______,BC、DC、CE之间的数量关系为______;
设,.
当点D在BC延长线上移动时,与之间有什么数量关系?请说明理由;
当点D在直线BC上不与B,C两点重合移动时,与之间有什么数量关系?请直接写出你的结论.
当时,若中最小角为,试探究的度数直接写出结果,无需写出求解过程.
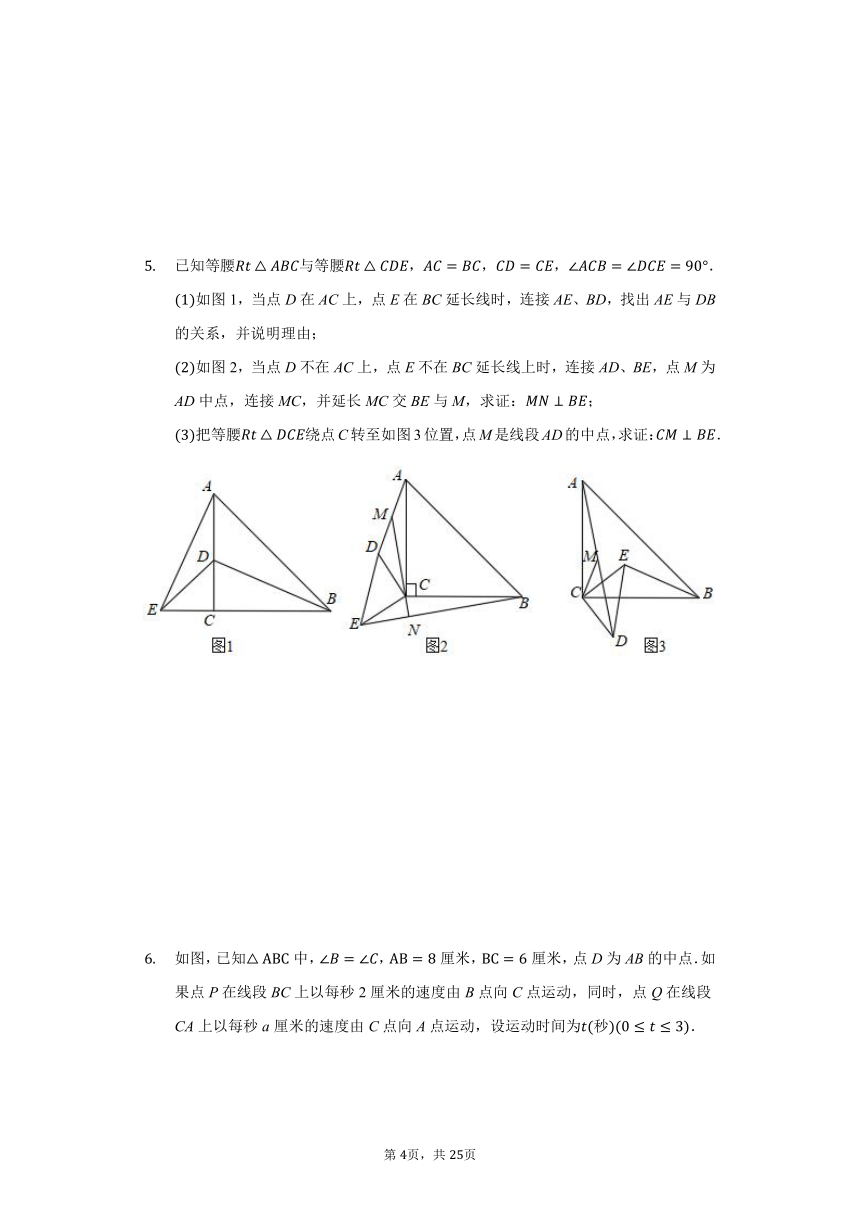
如图,,,,点P在线段AB上以的速度由点A向点B运动,同时,点Q在射线BD上由点B向点D运动.它们运动的时间为,当点P到达点B时,点Q也停止运动.
若点Q的运动速度与点P的运动速度相等,当时,与全等,此时吗?请说明理由.
将图中的“,”为改“”后得到如图,其他条件不变.设点Q的运动速度为,当点P、Q运动到某处时,有与全等,求出相应的x、t的值.
在成立的条件下且P、Q两点的运动速度相同时,______直接写出结果
已知等腰与等腰,,,.
如图1,当点D在AC上,点E在BC延长线时,连接AE、BD,找出AE与DB的关系,并说明理由;
如图2,当点D不在AC上,点E不在BC延长线上时,连接AD、BE,点M为AD中点,连接MC,并延长MC交BE与M,求证:;
把等腰绕点C转至如图3位置,点M是线段AD的中点,求证:.
如图,已知中,,厘米,厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为秒.
用的代数式表示PC的长度;
若点P、Q的运动速度相等,经过1秒后,与是否全等,请说明理由;
若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使与全等?
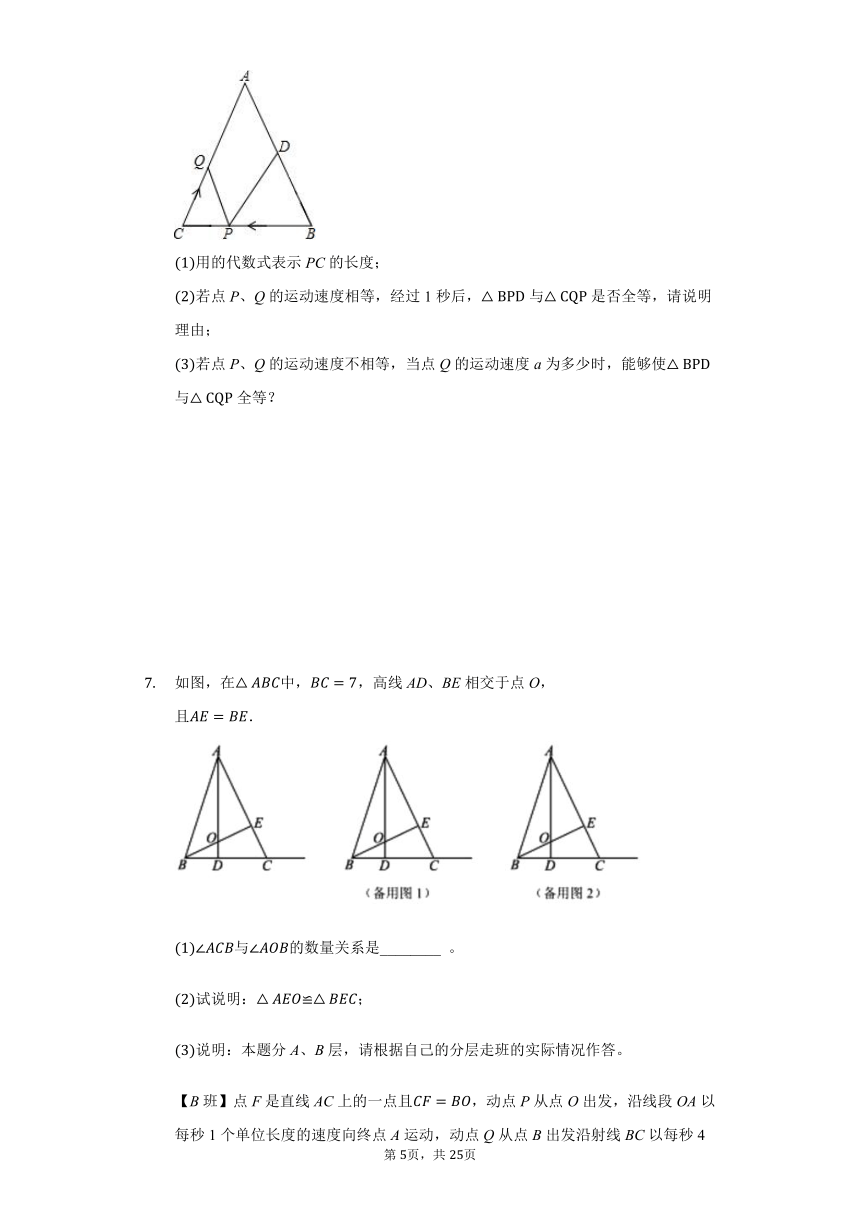
如图,在中,,高线AD、BE相交于点O,且.
与的数量关系是________
。
试说明:≌;
说明:本题分A、B层,请根据自己的分层走班的实际情况作答。
【B班】点F是直线AC上的一点且,动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动。设点P的运动时间为t秒,问是否存在t值,使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等若存在,请在备用图中画出大致示意图,并直接写出符合条件的t值:若不存在,请说明理由??
【A班】作图题:在如图所示的的方格中,每个小方格都是边长为1的正方形,是格点三角形即顶点恰好是正方形的顶点,请做出与有一条公共边且全等的所有格点三角形.
如图,在中,,,过点C作射线点M从点B出发,以的速度沿BC匀速移动;点N从点C出发,以的速度沿CD匀速移动.点M、N同时出发,当点M到达点C时,点M、N同时停止移动.连接AM、MN,设移动时间为.
点M、N从移动开始到停止,所用时间为______________s;
当与全等时,
若点M、N的移动速度相同,求t的值;
若点M、N的移动速度不同,求a的值;
如图,当点M、N开始移动时,点P同时从点A出发,以的速度沿AB向点B匀速移动,到达点B后立刻以原速度沿BA返回.当点M到达点C时,点M、N、P同时停止移动.在移动的过程中,是否存在与全等的情形若存在,求出t的值;若不存在,说明理由.
如图,在中,,高线AD、BE相交于点O,且.
与的数量关系是______;
试说明:≌;
点F是直线AC上的一点且,动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动.设点P的运动时间为t秒,问是否存在t值,使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等?若存在,请在备用图中画出大致示意图,并直接写出符合条件的t值;若不存在,请说明理由.
如图1,在中,,,直线DE经过点C,过点A,B分别作,,垂足分别为点D和E;,;
求证:≌;
求DE的长;
如图2,点M以3个单位长度秒的速度从点C出发沿着边CA运动,到终点A,点N以8个单位长度秒的速度从点B出发沿着线运动,到终点,N两点同时出发,运动时间为t秒,当点N到达终点时,两点同时停止运动,过点M作于点P,过点N作于点Q;
当点N在线段CA上时,用含有t的代数式表示线段CN的长度;
当t为何值时,点M与点N重合;
当与全等时,则______.
答案和解析
或
解:当点P在BC上时,如图,
若的面积等于面积的一半;则,
此时,点P移动的距离为,
移动的时间为:秒,
当点P在BA上时,如图
若的面积等于面积的一半;则,即点P为BA中点,
此时,点P移动的距离为,
移动的时间为:秒,
故答案为:或;
≌,即,对应顶点为A与D,P与E,Q与F;
当点P在AC上,如图所示:
此时,,,
点Q移动的速度为,
当点P在AB上,如图所示:
此时,,,
即,点P移动的距离为,点Q移动的距离为,
点Q移动的速度为,
综上所述,两点运动过程中的某一时刻,恰好≌,点Q的运动速为或.
2.
解:如图1,
把绕点A逆时针旋转至,使AB与AD重合,
,,,,
,
、D、G共线,
,,
,
,
即,
在和中,
,
≌,
,
,
,
故答案为:;
成立,
理由:如图2,把绕A点旋转到,使AB和AD重合,
则,,,
,
,
、D、G在一条直线上,
与同理得,,
在和中,
,
≌,
,
,
;
解:中,,,
,
由勾股定理得:,
如图3,把绕A点旋转到,使AB和AC重合,连接DF.
则,,,
,
,
,
在和中,
≌,
,
设,则,
,
,
,,
,
由勾股定理得:,
,
解得:,
即.
3.
?
?
解:如图1所示:,
,
,
在和中,,
≌,
,,
,
,
,
,
,
故答案为:;;;
当点D在线段BC的延长线上移动时,与之间的数量关系是,理由如下:
,
,
,
在和中,,
≌,
,
,
,
,,
;
分三种情况:
Ⅰ当D在线段BC上时,,如图2所示,理由如下:
同理可证明:≌,
,,
,
,
,
,,
;
Ⅱ当点D在线段BC反向延长线上时,,如图3所示,理由如下:
同理可证明:≌,
,
,,
,
,
,,
;
Ⅲ当点D在线段BC的延长线上时,如图1所示,;
综上所述,当点D在BC上移动时,或;
,理由如下:
当点D在线段BC的延长线上或在线段BC反向延长线上移动时,,
即,
,
,
,
,
,
是等边三角形,
;
当D在线段BC上时,,
即,
,
,
,
,
,
是等边三角形,
;
综上所述,当时,若中最小角为,的度数为.
4.
解:≌,
,
,
,
,
在和中,,
≌;
,
,
,
,
;
存在x的值,使得与全等,
若≌,
则,,可得:,
解得:,;
若≌,
则,,可得:,
解得:,;
、Q两点的运动速度相同,
、Q两点的运动速度为2,
,
,
,
,
在和中,,
≌;
,
,
,
.
故答案为:.
5.
解:,,
理由如下:如图1,延长BD交AE于H,
,,,
≌,
,,
,
,
,
;
如图2,过点D作交CM的延长线于G,
,
,
点M为AD中点,
,
又,,
≌,
,
,,
,,,
,
,
,
又,,
≌,
,
,
,
;
如图3,过点A作,交CM的延长线于Q,延长BE交CQ于P,
点M是线段AD的中点,
,
,
,
又,,
≌,
,
,
,
,
,
,
,
又,,
≌,
,
,
,
,
.
6.
解:,则;
和全等.
理由:秒厘米,
厘米,
厘米,点D为AB的中点,
厘米.
,
在和中,
,
≌;
点P、Q的运动速度不相等,
又≌,,
,,
点P,点Q运动的时间秒,
厘米秒.
7.
解:;
如图1,是高,
,
由得:,
,
,
在和中,
,
≌.
【B班】
存在.由题意得:,,
,,
当Q在边BC上时,如图2,≌,
,即,
,
当Q在BC的延长线上时,如图3,≌,
,
即,
,
综上所述,当秒或秒时,以点B,O,P为顶点的三角形与以点F,C,Q为顶点的三角形全等.
故满足条件的t的值为或;
【A班】
如图所示:
【B班】
分两种情形:当Q在边BC上时,如图2,≌,当Q在BC的延长线上时,如图3,≌,分别构建方程求解即可.
【A班】
此题主要考查了作图应用与设计作图,全等三角形的判定,关键是考虑全面,不要漏解.以BC为公共边时有3个三角形,以AC为公共边时有1个三角形与全等.
【解答】
解:结论:.
理由:如图1中,
,BE是的高,
,
,
,
.
故答案为.
8.
解:;
,
,
与全等,
≌或≌,
由题意得:,
≌
,
,
解得:;??????????????????????????????????
由题意得:,
≌,
,,
BC,
,
解得:;
,
解得:;
存在
,
,
与全等,
≌或≌,
当≌时,则,
若此时P由A向B运动,则,,
,
,
解得:舍去
若此时P由B向A运动,则,,
,
,
解得:;
当≌时,则,,
BC
,
解得:
当时,点P的路程为,
此时,
则,
即,
,
符合题意,
综上所述,满足条件的t的值有:或.
解:点M的运动时间为
故答案为;
9.
解:结论:.
理由:如图1中,
,BE是的高,
,
,
,
.
故答案为:.
如图1,是高,
,
由得:,
,
,
在和中,
,
≌.
存在.由题意得:,,
,,
当Q在边BC上时,如图2,≌,
,即,
,
当Q在BC的延长线上时,如图3,≌,
,
即,
,
综上所述,当秒或秒时,以点B,O,P为顶点的三角形与以点F,C,Q为顶点的三角形全等.
故满足条件的t的值为或.
10.
或2s
证明:,,
,
,
,
,
在和中,,
≌;
由得:≌,
,,
;
解:当点N在线段CA上时,如图3所示:
;
点M与点N重合时,,
即,
解得:,
当t为2秒时,点M与点N重合;
分两种情况:
当点N在线段BC上时,≌,
,
,
解得:;
当点N在线段CA上时,≌,点M与N重合,,
则,
解得:;
综上所述,当与全等时,则t等于或2s,
故答案为:或2s.
第2页,共2页
第1页,共1页
班级:___________姓名:___________得分:___________
一、解答题
如图,在中,,,,,现有一动点P,从点A出发,沿着三角形的边运动,回到点A停止,速度为,设运动时间为ts.
如图,当______时,的面积等于面积的一半;
如图,在中,,,,在的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边运动,回到点A停止.在两点运动过程中的某一时刻,恰好≌,求点Q的运动速度.
探究:如图1和图2,四边形ABCD中,已知,,点E、F分别在BC、CD上,.
如图1,若、都是直角,把绕点A逆时针旋转至,使AB与AD重合,直接写出线段BE、DF和EF之间的数量关系______;
如图2,若、都不是直角,但满足,线段BE、DF和EF之间的结论是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由.
拓展:如图3,在中,,点D、E均在边BC边上,且,若,求DE的长.
在中,,D是直线BC上一点,以AD为一条边在AD的右侧作,使,,连接CE.
如图,当点D在BC延长线上移动时,若,则______,______,BC、DC、CE之间的数量关系为______;
设,.
当点D在BC延长线上移动时,与之间有什么数量关系?请说明理由;
当点D在直线BC上不与B,C两点重合移动时,与之间有什么数量关系?请直接写出你的结论.
当时,若中最小角为,试探究的度数直接写出结果,无需写出求解过程.
如图,,,,点P在线段AB上以的速度由点A向点B运动,同时,点Q在射线BD上由点B向点D运动.它们运动的时间为,当点P到达点B时,点Q也停止运动.
若点Q的运动速度与点P的运动速度相等,当时,与全等,此时吗?请说明理由.
将图中的“,”为改“”后得到如图,其他条件不变.设点Q的运动速度为,当点P、Q运动到某处时,有与全等,求出相应的x、t的值.
在成立的条件下且P、Q两点的运动速度相同时,______直接写出结果
已知等腰与等腰,,,.
如图1,当点D在AC上,点E在BC延长线时,连接AE、BD,找出AE与DB的关系,并说明理由;
如图2,当点D不在AC上,点E不在BC延长线上时,连接AD、BE,点M为AD中点,连接MC,并延长MC交BE与M,求证:;
把等腰绕点C转至如图3位置,点M是线段AD的中点,求证:.
如图,已知中,,厘米,厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为秒.
用的代数式表示PC的长度;
若点P、Q的运动速度相等,经过1秒后,与是否全等,请说明理由;
若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使与全等?
如图,在中,,高线AD、BE相交于点O,且.
与的数量关系是________
。
试说明:≌;
说明:本题分A、B层,请根据自己的分层走班的实际情况作答。
【B班】点F是直线AC上的一点且,动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动。设点P的运动时间为t秒,问是否存在t值,使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等若存在,请在备用图中画出大致示意图,并直接写出符合条件的t值:若不存在,请说明理由??
【A班】作图题:在如图所示的的方格中,每个小方格都是边长为1的正方形,是格点三角形即顶点恰好是正方形的顶点,请做出与有一条公共边且全等的所有格点三角形.
如图,在中,,,过点C作射线点M从点B出发,以的速度沿BC匀速移动;点N从点C出发,以的速度沿CD匀速移动.点M、N同时出发,当点M到达点C时,点M、N同时停止移动.连接AM、MN,设移动时间为.
点M、N从移动开始到停止,所用时间为______________s;
当与全等时,
若点M、N的移动速度相同,求t的值;
若点M、N的移动速度不同,求a的值;
如图,当点M、N开始移动时,点P同时从点A出发,以的速度沿AB向点B匀速移动,到达点B后立刻以原速度沿BA返回.当点M到达点C时,点M、N、P同时停止移动.在移动的过程中,是否存在与全等的情形若存在,求出t的值;若不存在,说明理由.
如图,在中,,高线AD、BE相交于点O,且.
与的数量关系是______;
试说明:≌;
点F是直线AC上的一点且,动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动.设点P的运动时间为t秒,问是否存在t值,使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等?若存在,请在备用图中画出大致示意图,并直接写出符合条件的t值;若不存在,请说明理由.
如图1,在中,,,直线DE经过点C,过点A,B分别作,,垂足分别为点D和E;,;
求证:≌;
求DE的长;
如图2,点M以3个单位长度秒的速度从点C出发沿着边CA运动,到终点A,点N以8个单位长度秒的速度从点B出发沿着线运动,到终点,N两点同时出发,运动时间为t秒,当点N到达终点时,两点同时停止运动,过点M作于点P,过点N作于点Q;
当点N在线段CA上时,用含有t的代数式表示线段CN的长度;
当t为何值时,点M与点N重合;
当与全等时,则______.
答案和解析
或
解:当点P在BC上时,如图,
若的面积等于面积的一半;则,
此时,点P移动的距离为,
移动的时间为:秒,
当点P在BA上时,如图
若的面积等于面积的一半;则,即点P为BA中点,
此时,点P移动的距离为,
移动的时间为:秒,
故答案为:或;
≌,即,对应顶点为A与D,P与E,Q与F;
当点P在AC上,如图所示:
此时,,,
点Q移动的速度为,
当点P在AB上,如图所示:
此时,,,
即,点P移动的距离为,点Q移动的距离为,
点Q移动的速度为,
综上所述,两点运动过程中的某一时刻,恰好≌,点Q的运动速为或.
2.
解:如图1,
把绕点A逆时针旋转至,使AB与AD重合,
,,,,
,
、D、G共线,
,,
,
,
即,
在和中,
,
≌,
,
,
,
故答案为:;
成立,
理由:如图2,把绕A点旋转到,使AB和AD重合,
则,,,
,
,
、D、G在一条直线上,
与同理得,,
在和中,
,
≌,
,
,
;
解:中,,,
,
由勾股定理得:,
如图3,把绕A点旋转到,使AB和AC重合,连接DF.
则,,,
,
,
,
在和中,
≌,
,
设,则,
,
,
,,
,
由勾股定理得:,
,
解得:,
即.
3.
?
?
解:如图1所示:,
,
,
在和中,,
≌,
,,
,
,
,
,
,
故答案为:;;;
当点D在线段BC的延长线上移动时,与之间的数量关系是,理由如下:
,
,
,
在和中,,
≌,
,
,
,
,,
;
分三种情况:
Ⅰ当D在线段BC上时,,如图2所示,理由如下:
同理可证明:≌,
,,
,
,
,
,,
;
Ⅱ当点D在线段BC反向延长线上时,,如图3所示,理由如下:
同理可证明:≌,
,
,,
,
,
,,
;
Ⅲ当点D在线段BC的延长线上时,如图1所示,;
综上所述,当点D在BC上移动时,或;
,理由如下:
当点D在线段BC的延长线上或在线段BC反向延长线上移动时,,
即,
,
,
,
,
,
是等边三角形,
;
当D在线段BC上时,,
即,
,
,
,
,
,
是等边三角形,
;
综上所述,当时,若中最小角为,的度数为.
4.
解:≌,
,
,
,
,
在和中,,
≌;
,
,
,
,
;
存在x的值,使得与全等,
若≌,
则,,可得:,
解得:,;
若≌,
则,,可得:,
解得:,;
、Q两点的运动速度相同,
、Q两点的运动速度为2,
,
,
,
,
在和中,,
≌;
,
,
,
.
故答案为:.
5.
解:,,
理由如下:如图1,延长BD交AE于H,
,,,
≌,
,,
,
,
,
;
如图2,过点D作交CM的延长线于G,
,
,
点M为AD中点,
,
又,,
≌,
,
,,
,,,
,
,
,
又,,
≌,
,
,
,
;
如图3,过点A作,交CM的延长线于Q,延长BE交CQ于P,
点M是线段AD的中点,
,
,
,
又,,
≌,
,
,
,
,
,
,
,
又,,
≌,
,
,
,
,
.
6.
解:,则;
和全等.
理由:秒厘米,
厘米,
厘米,点D为AB的中点,
厘米.
,
在和中,
,
≌;
点P、Q的运动速度不相等,
又≌,,
,,
点P,点Q运动的时间秒,
厘米秒.
7.
解:;
如图1,是高,
,
由得:,
,
,
在和中,
,
≌.
【B班】
存在.由题意得:,,
,,
当Q在边BC上时,如图2,≌,
,即,
,
当Q在BC的延长线上时,如图3,≌,
,
即,
,
综上所述,当秒或秒时,以点B,O,P为顶点的三角形与以点F,C,Q为顶点的三角形全等.
故满足条件的t的值为或;
【A班】
如图所示:
【B班】
分两种情形:当Q在边BC上时,如图2,≌,当Q在BC的延长线上时,如图3,≌,分别构建方程求解即可.
【A班】
此题主要考查了作图应用与设计作图,全等三角形的判定,关键是考虑全面,不要漏解.以BC为公共边时有3个三角形,以AC为公共边时有1个三角形与全等.
【解答】
解:结论:.
理由:如图1中,
,BE是的高,
,
,
,
.
故答案为.
8.
解:;
,
,
与全等,
≌或≌,
由题意得:,
≌
,
,
解得:;??????????????????????????????????
由题意得:,
≌,
,,
BC,
,
解得:;
,
解得:;
存在
,
,
与全等,
≌或≌,
当≌时,则,
若此时P由A向B运动,则,,
,
,
解得:舍去
若此时P由B向A运动,则,,
,
,
解得:;
当≌时,则,,
BC
,
解得:
当时,点P的路程为,
此时,
则,
即,
,
符合题意,
综上所述,满足条件的t的值有:或.
解:点M的运动时间为
故答案为;
9.
解:结论:.
理由:如图1中,
,BE是的高,
,
,
,
.
故答案为:.
如图1,是高,
,
由得:,
,
,
在和中,
,
≌.
存在.由题意得:,,
,,
当Q在边BC上时,如图2,≌,
,即,
,
当Q在BC的延长线上时,如图3,≌,
,
即,
,
综上所述,当秒或秒时,以点B,O,P为顶点的三角形与以点F,C,Q为顶点的三角形全等.
故满足条件的t的值为或.
10.
或2s
证明:,,
,
,
,
,
在和中,,
≌;
由得:≌,
,,
;
解:当点N在线段CA上时,如图3所示:
;
点M与点N重合时,,
即,
解得:,
当t为2秒时,点M与点N重合;
分两种情况:
当点N在线段BC上时,≌,
,
,
解得:;
当点N在线段CA上时,≌,点M与N重合,,
则,
解得:;
综上所述,当与全等时,则t等于或2s,
故答案为:或2s.
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
