北师大版九年级数学下册 1.2 30°,45 °,60°角的三角函数值同步练习(word 版 含答案)
文档属性
| 名称 | 北师大版九年级数学下册 1.2 30°,45 °,60°角的三角函数值同步练习(word 版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 514.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 16:03:33 | ||
图片预览


文档简介
1.2
30°,45
°,60°角的三角函数值
一、选择题
1.2cos60°的值为( )
A.1
B.
C.
D.
2.计算sin245°+cos245°的值为( )
A.0
B.
C.1
D.2
3.在△ABC中,若∠C=90°,tanA=,则sinB的值为( )
A.
B.
C.
D.
4.如图1,将三角尺的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的余弦值是( )
图1
A.
B.
C.
D.
5.在△ABC中,∠A,∠B均为锐角,若+(1-tanB)2=0,则∠C的度数是( )
A.45°
B.60°
C.75°
D.105°
6.菱形OABC在平面直角坐标系中的位置如图2所示,若∠AOC=45°,OC=,则点B的坐标为( )
图2
A.(,1)
B.(1,)
C.(+1,1)
D.(1,+1)
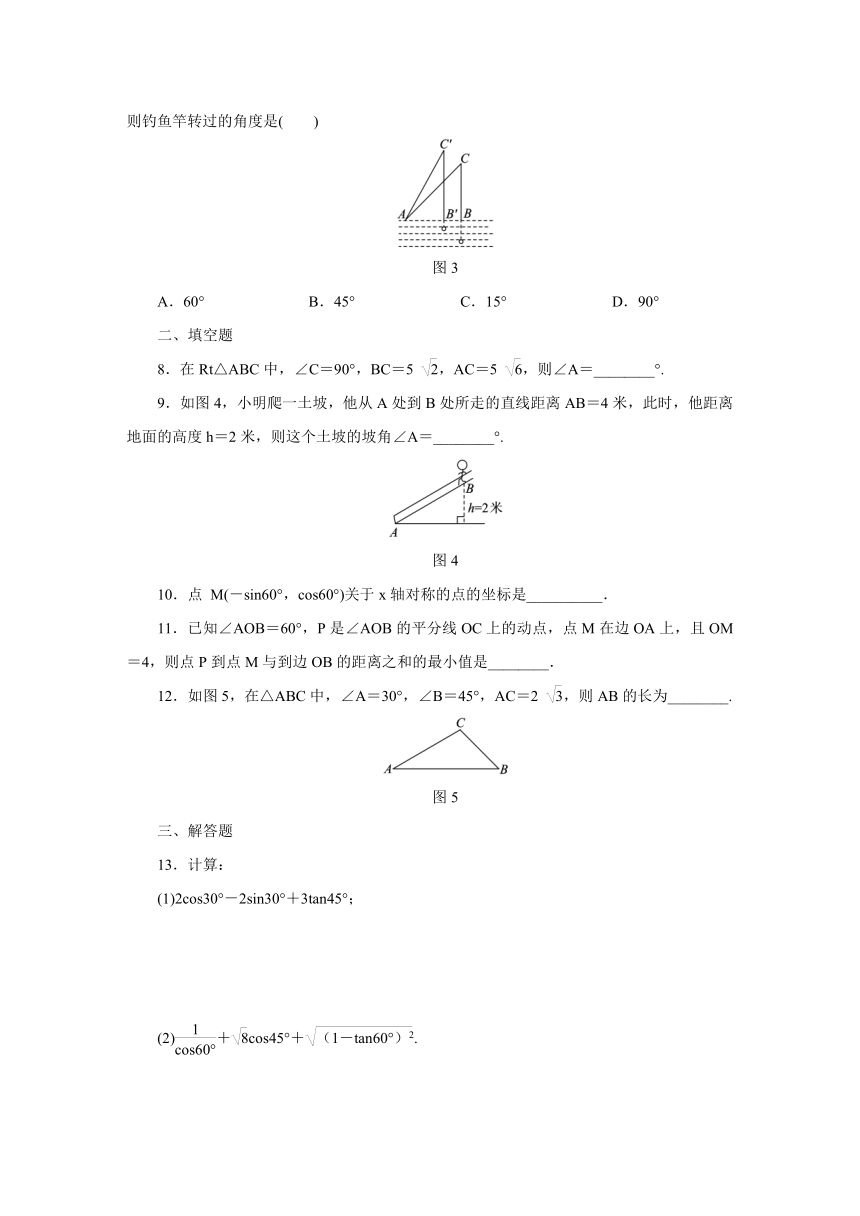
7.如图3所示,钓鱼竿AC长6
m,露在水面上的渔线BC长3
m,某钓鱼者想看看鱼钩上的情况,把钓鱼竿AC转动到AC′的位置,此时露在水面上的渔线B′C′长3
m,则钓鱼竿转过的角度是( )
图3
A.60°
B.45°
C.15°
D.90°
二、填空题
8.在Rt△ABC中,∠C=90°,BC=5
,AC=5
,则∠A=________°.
9.如图4,小明爬一土坡,他从A处到B处所走的直线距离AB=4米,此时,他距离地面的高度h=2米,则这个土坡的坡角∠A=________°.
图4
10.点
M(-sin60°,cos60°)关于x轴对称的点的坐标是__________.
11.已知∠AOB=60°,P是∠AOB的平分线OC上的动点,点M在边OA上,且OM=4,则点P到点M与到边OB的距离之和的最小值是________.
12.如图5,在△ABC中,∠A=30°,∠B=45°,AC=2
,则AB的长为________.
图5
三、解答题
13.计算:
(1)2cos30°-2sin30°+3tan45°;
(2)+cos45°+.
14.已知α为锐角,sin(α+15°)=,求-4cosα+tanα+()-1的值.
15.如图6,梯子的长为2.8
m(即AB=AC=2.8
m),当α=60°时,求梯子顶端离地面的高度AD和两梯脚之间的距离BC.当α=45°时呢?
图6
16.如图7,一数学兴趣小组为测量河对岸树AB的高,在河岸边选择一点C,从C处测得树梢A的仰角为45°,沿BC方向后退10米到点D,再次测得点A的仰角为30°.求树AB的高.(结果精确到0.1米,参考数据:≈1.414,≈1.732)
图7
答案
1.
A
2.
C
3.
C
4.
A
5.
C .
6.
C
7.
C
8.
30
9.
30
10.
11.
2
12.
3+
13.解:(1)原式=2×-2×+3×1
=-1+3
=+2.
(2)原式=+×+
=2+2+-1
=+3.
14.解:∵sin(α+15°)=,α为锐角,
∴α=45°,
∴-4cosα+tanα+()-1=2
-4×+1+3=4.
15.解:∵AB=AC,AD⊥BC,
∴BC=2BD.
当α=60°时,在Rt△ABD中,∠ADB=90°,AB=2.8
m,∠ABD=60°,
∴BD=AB·cos∠ABD=1.4
m,AD=AB·sin∠ABD=
m,
∴BC=2BD=2.8
m.
当α=45°时,在Rt△ABD中,∠ADB=90°,AB=2.8
m,∠ABD=45°,
∴BD=AB·cos∠ABD=
m,AD=AB·sin∠ABD=
m,
∴BC=2BD=
m.
16.解:由题意,得∠B=90°,∠D=30°,∠ACB=45°,DC=10米.
设AB=x米,则在Rt△ABC中,CB===x米,在Rt△ABD中,DB===x米.
因为DB=DC+CB,
所以x=x+10,
所以(-1)x=10,
所以x==5
+5≈5×1.732+5=8.66+5=13.66≈13.7(米).
答:树AB的高约为13.7米.
30°,45
°,60°角的三角函数值
一、选择题
1.2cos60°的值为( )
A.1
B.
C.
D.
2.计算sin245°+cos245°的值为( )
A.0
B.
C.1
D.2
3.在△ABC中,若∠C=90°,tanA=,则sinB的值为( )
A.
B.
C.
D.
4.如图1,将三角尺的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的余弦值是( )
图1
A.
B.
C.
D.
5.在△ABC中,∠A,∠B均为锐角,若+(1-tanB)2=0,则∠C的度数是( )
A.45°
B.60°
C.75°
D.105°
6.菱形OABC在平面直角坐标系中的位置如图2所示,若∠AOC=45°,OC=,则点B的坐标为( )
图2
A.(,1)
B.(1,)
C.(+1,1)
D.(1,+1)
7.如图3所示,钓鱼竿AC长6
m,露在水面上的渔线BC长3
m,某钓鱼者想看看鱼钩上的情况,把钓鱼竿AC转动到AC′的位置,此时露在水面上的渔线B′C′长3
m,则钓鱼竿转过的角度是( )
图3
A.60°
B.45°
C.15°
D.90°
二、填空题
8.在Rt△ABC中,∠C=90°,BC=5
,AC=5
,则∠A=________°.
9.如图4,小明爬一土坡,他从A处到B处所走的直线距离AB=4米,此时,他距离地面的高度h=2米,则这个土坡的坡角∠A=________°.
图4
10.点
M(-sin60°,cos60°)关于x轴对称的点的坐标是__________.
11.已知∠AOB=60°,P是∠AOB的平分线OC上的动点,点M在边OA上,且OM=4,则点P到点M与到边OB的距离之和的最小值是________.
12.如图5,在△ABC中,∠A=30°,∠B=45°,AC=2
,则AB的长为________.
图5
三、解答题
13.计算:
(1)2cos30°-2sin30°+3tan45°;
(2)+cos45°+.
14.已知α为锐角,sin(α+15°)=,求-4cosα+tanα+()-1的值.
15.如图6,梯子的长为2.8
m(即AB=AC=2.8
m),当α=60°时,求梯子顶端离地面的高度AD和两梯脚之间的距离BC.当α=45°时呢?
图6
16.如图7,一数学兴趣小组为测量河对岸树AB的高,在河岸边选择一点C,从C处测得树梢A的仰角为45°,沿BC方向后退10米到点D,再次测得点A的仰角为30°.求树AB的高.(结果精确到0.1米,参考数据:≈1.414,≈1.732)
图7
答案
1.
A
2.
C
3.
C
4.
A
5.
C .
6.
C
7.
C
8.
30
9.
30
10.
11.
2
12.
3+
13.解:(1)原式=2×-2×+3×1
=-1+3
=+2.
(2)原式=+×+
=2+2+-1
=+3.
14.解:∵sin(α+15°)=,α为锐角,
∴α=45°,
∴-4cosα+tanα+()-1=2
-4×+1+3=4.
15.解:∵AB=AC,AD⊥BC,
∴BC=2BD.
当α=60°时,在Rt△ABD中,∠ADB=90°,AB=2.8
m,∠ABD=60°,
∴BD=AB·cos∠ABD=1.4
m,AD=AB·sin∠ABD=
m,
∴BC=2BD=2.8
m.
当α=45°时,在Rt△ABD中,∠ADB=90°,AB=2.8
m,∠ABD=45°,
∴BD=AB·cos∠ABD=
m,AD=AB·sin∠ABD=
m,
∴BC=2BD=
m.
16.解:由题意,得∠B=90°,∠D=30°,∠ACB=45°,DC=10米.
设AB=x米,则在Rt△ABC中,CB===x米,在Rt△ABD中,DB===x米.
因为DB=DC+CB,
所以x=x+10,
所以(-1)x=10,
所以x==5
+5≈5×1.732+5=8.66+5=13.66≈13.7(米).
答:树AB的高约为13.7米.
