北师大版九年级数学下册同步练习:1.4 解直角三角形(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学下册同步练习:1.4 解直角三角形(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 290.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 16:19:10 | ||
图片预览



文档简介
1.4
解直角三角形
一、选择题
1.如图1,在Rt△ABC中,∠C=90°,AC=5,∠A=60°,则BC的长是( )
图1
A.5
B.5
C.5
D.10
2.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,a=,b=,则∠B的度数为
()
A.30°
B.45°
C.60°
D.75°
3.如图2,在△ABC中,AD⊥BC于点D,AD=BD,若AB=4
,tanC=,则BC的长为( )
图2
A.8
B.8
C.7
D.7
4.如果三角形中一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的是( )
A.1,2,3
B.1,1,
C.1,1,
D.1,2,
5.如图3,矩形ABCD的对角线交于点O,已知AB=m,∠BAC=∠α,则下列结论错误的是( )
图3
A.∠BDC=∠α
B.BC=m·tanα
C.AO=
D.BD=
二、填空题
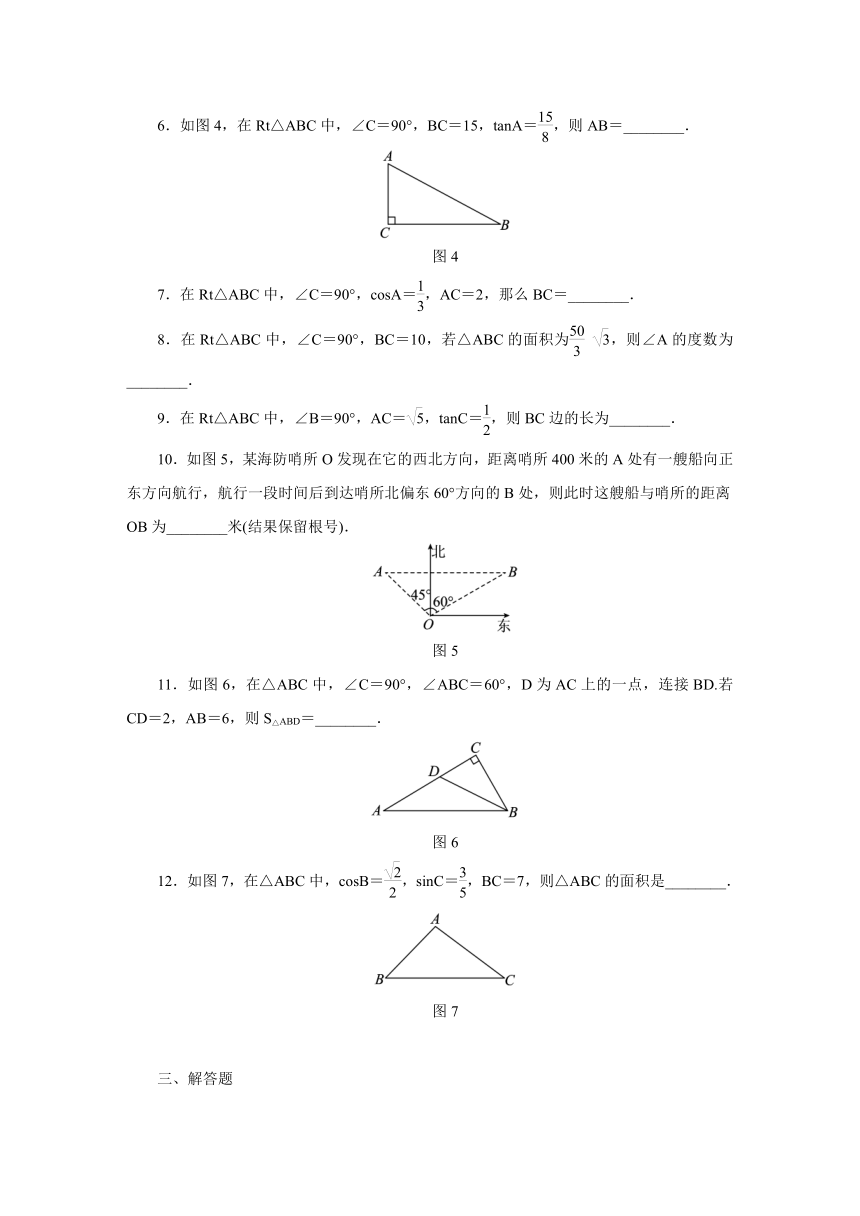
6.如图4,在Rt△ABC中,∠C=90°,BC=15,tanA=,则AB=________.
图4
7.在Rt△ABC中,∠C=90°,cosA=,AC=2,那么BC=________.
8.在Rt△ABC中,∠C=90°,BC=10,若△ABC的面积为
,则∠A的度数为________.
9.在Rt△ABC中,∠B=90°,AC=,tanC=,则BC边的长为________.
10.如图5,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB为________米(结果保留根号).
图5
11.如图6,在△ABC中,∠C=90°,∠ABC=60°,D为AC上的一点,连接BD.若CD=2,AB=6,则S△ABD=________.
图6
12.如图7,在△ABC中,cosB=,sinC=,BC=7,则△ABC的面积是________.
图7
三、解答题
13.(1)在Rt△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且a=,c=2,求这个三角形的其他元素.
(2)在Rt△ABC中,∠C=90°,∠B=55°,AC=4,求这个三角形的其他元素(边长精确到0.1).
14.已知Rt△ABC在直角坐标系中的位置如图8所示,求A,C两点的坐标.
图8
15.如图9,已知在四边形ABCD中,∠ABC=∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
(1)若∠A=60°,求BC的长;
(2)若sinA=,求AD的长.
图9
16.两个城镇A,B与两条公路ME,MF的位置如图10所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A,B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.
(1)点C应选在何处?请在图中用尺规作图找出符合条件的点C(不写已知、求作、作法,只保留作图痕迹);
(2)设AB的垂直平分线交ME于点N,且MN=2(+1)km,测得∠CMN=30°,∠CNM=45°,求点C到公路ME的距离.
图10
答案
1.A
2.A
3.C
4.D
5.C
6.17
7.4
8.60°
9.2
10.400
11.-3
12.
13.解:(1)在Rt△ABC中,
b===1.
因为sinA==,
所以∠A=60°,所以∠B=30°.
(2)根据题意,得∠A=90°-∠B=90°-55°=35°.
在Rt△ABC中,sinB=,则AB==≈4.9.
在Rt△ABC中,tanB=,则BC==≈2.8.
14.解:如图所示,过点A作AD⊥BC于点D.
∵BC===4,
∴点C的坐标为(4,0).
在Rt△ABD中,sin30°=,cos30°=,而AB=2
,∴AD=ABsin30°=2
×=,
BD=ABcos30°=2
×=3,
∴点A的坐标为(3,).
15.解:(1)∵∠A=60°,∠ABE=90°,AB=6,tanA=,
∴∠E=30°,BE=tan60°·6=6
.
∵∠CDE=90°,CD=4,sinE=,∠E=30°,
∴CE==8,
∴BC=BE-CE=6
-8.
(2)∵∠ABE=90°,AB=6,sinA==,
∴设BE=4x,则AE=5x,由勾股定理得AB=3x,
∴3x=6,解得x=2,
∴BE=8,AE=10,
∴tanE====,
解得DE=,
∴AD=AE-DE=10-=,
即AD的长是.
16.解:(1)如图①所示:
点C即为所求.
(2)过点C作CD⊥MN于点D,如图②所示.
∵在Rt△CMD中,∠CMN=30°,
tan∠CMN=,
∴MD===CD.
∵在Rt△CND中,∠CNM=45°,tan∠CNM=,∴DN==CD.
∵MN=2(+1)km,
∴MN=MD+DN=CD+CD=2(+1),
解得CD=2(km).
∴点C到公路ME的距离为2
km.
解直角三角形
一、选择题
1.如图1,在Rt△ABC中,∠C=90°,AC=5,∠A=60°,则BC的长是( )
图1
A.5
B.5
C.5
D.10
2.在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,a=,b=,则∠B的度数为
()
A.30°
B.45°
C.60°
D.75°
3.如图2,在△ABC中,AD⊥BC于点D,AD=BD,若AB=4
,tanC=,则BC的长为( )
图2
A.8
B.8
C.7
D.7
4.如果三角形中一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的是( )
A.1,2,3
B.1,1,
C.1,1,
D.1,2,
5.如图3,矩形ABCD的对角线交于点O,已知AB=m,∠BAC=∠α,则下列结论错误的是( )
图3
A.∠BDC=∠α
B.BC=m·tanα
C.AO=
D.BD=
二、填空题
6.如图4,在Rt△ABC中,∠C=90°,BC=15,tanA=,则AB=________.
图4
7.在Rt△ABC中,∠C=90°,cosA=,AC=2,那么BC=________.
8.在Rt△ABC中,∠C=90°,BC=10,若△ABC的面积为
,则∠A的度数为________.
9.在Rt△ABC中,∠B=90°,AC=,tanC=,则BC边的长为________.
10.如图5,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB为________米(结果保留根号).
图5
11.如图6,在△ABC中,∠C=90°,∠ABC=60°,D为AC上的一点,连接BD.若CD=2,AB=6,则S△ABD=________.
图6
12.如图7,在△ABC中,cosB=,sinC=,BC=7,则△ABC的面积是________.
图7
三、解答题
13.(1)在Rt△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且a=,c=2,求这个三角形的其他元素.
(2)在Rt△ABC中,∠C=90°,∠B=55°,AC=4,求这个三角形的其他元素(边长精确到0.1).
14.已知Rt△ABC在直角坐标系中的位置如图8所示,求A,C两点的坐标.
图8
15.如图9,已知在四边形ABCD中,∠ABC=∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
(1)若∠A=60°,求BC的长;
(2)若sinA=,求AD的长.
图9
16.两个城镇A,B与两条公路ME,MF的位置如图10所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A,B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.
(1)点C应选在何处?请在图中用尺规作图找出符合条件的点C(不写已知、求作、作法,只保留作图痕迹);
(2)设AB的垂直平分线交ME于点N,且MN=2(+1)km,测得∠CMN=30°,∠CNM=45°,求点C到公路ME的距离.
图10
答案
1.A
2.A
3.C
4.D
5.C
6.17
7.4
8.60°
9.2
10.400
11.-3
12.
13.解:(1)在Rt△ABC中,
b===1.
因为sinA==,
所以∠A=60°,所以∠B=30°.
(2)根据题意,得∠A=90°-∠B=90°-55°=35°.
在Rt△ABC中,sinB=,则AB==≈4.9.
在Rt△ABC中,tanB=,则BC==≈2.8.
14.解:如图所示,过点A作AD⊥BC于点D.
∵BC===4,
∴点C的坐标为(4,0).
在Rt△ABD中,sin30°=,cos30°=,而AB=2
,∴AD=ABsin30°=2
×=,
BD=ABcos30°=2
×=3,
∴点A的坐标为(3,).
15.解:(1)∵∠A=60°,∠ABE=90°,AB=6,tanA=,
∴∠E=30°,BE=tan60°·6=6
.
∵∠CDE=90°,CD=4,sinE=,∠E=30°,
∴CE==8,
∴BC=BE-CE=6
-8.
(2)∵∠ABE=90°,AB=6,sinA==,
∴设BE=4x,则AE=5x,由勾股定理得AB=3x,
∴3x=6,解得x=2,
∴BE=8,AE=10,
∴tanE====,
解得DE=,
∴AD=AE-DE=10-=,
即AD的长是.
16.解:(1)如图①所示:
点C即为所求.
(2)过点C作CD⊥MN于点D,如图②所示.
∵在Rt△CMD中,∠CMN=30°,
tan∠CMN=,
∴MD===CD.
∵在Rt△CND中,∠CNM=45°,tan∠CNM=,∴DN==CD.
∵MN=2(+1)km,
∴MN=MD+DN=CD+CD=2(+1),
解得CD=2(km).
∴点C到公路ME的距离为2
km.
