12.1轴对称(2)
图片预览






文档简介
(共25张PPT)
给我最大快乐的,
不是已懂的知识,
而是不断的学习. ----高斯
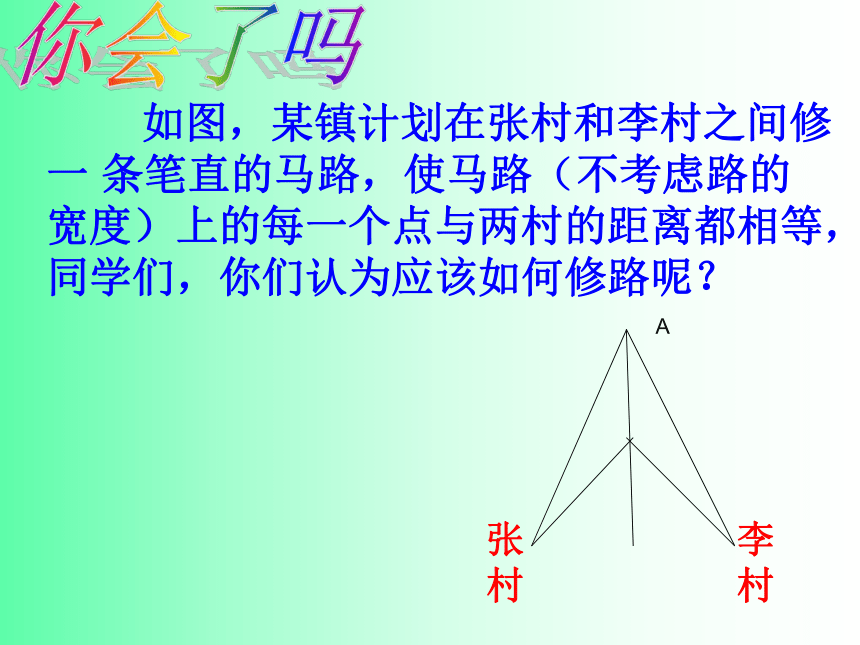
如图,某镇计划在张村和李村之间修一 条笔直的马路,使马路(不考虑路的宽度)上的每一个点与两村的距离都相等,同学们,你们认为应该如何修路呢?
A
张村
李村
1.什么样的图形是轴对称图形?
2.什么叫线段的垂直平分线?
3.线段是不是轴对称图形?如果是,请说出它的对称轴。
A
B
P1
P2
P3
L
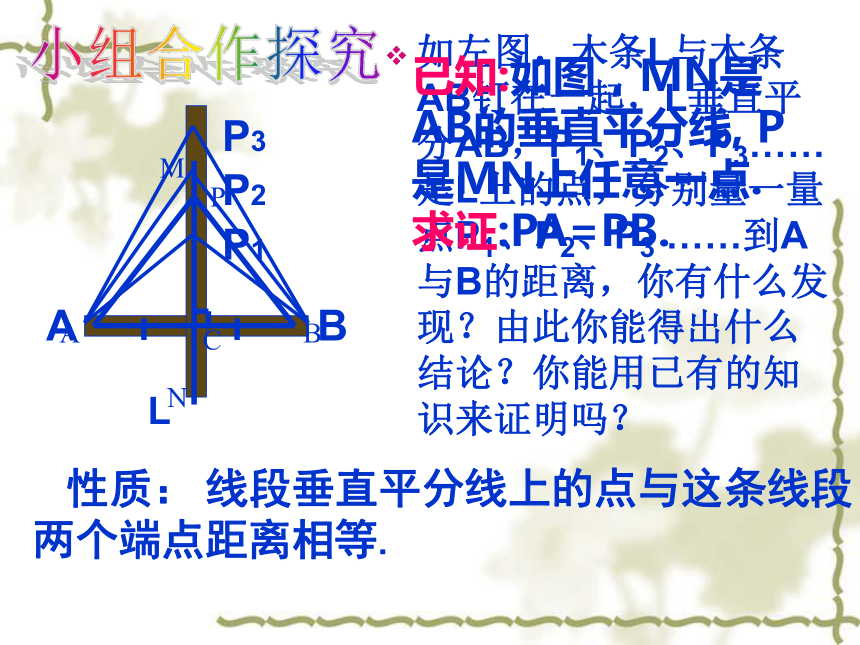
如左图,木条L与木条AB钉在一起,L垂直平分AB,P1、P2、P3……是L上的点,分别量一量点P1、P2、P3 ……到A与B的距离,你有什么发现?由此你能得出什么结论?你能用已有的知识来证明吗?
线段垂直平分线上的点与这条线段两个端点距离相等.
已知:如图,MN是AB的垂直平分线, P是MN上任意一点.
求证:PA=PB.
A
C
B
P
M
N
性质:
如图,某镇计划在张村和李村之间修一 条笔直的马路,使马路(不考虑路的宽度)上的每一个点与两村的距离都相等,同学们,你们认为应该如何修路呢?
A
张村
李村
反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
你能给出证明吗?
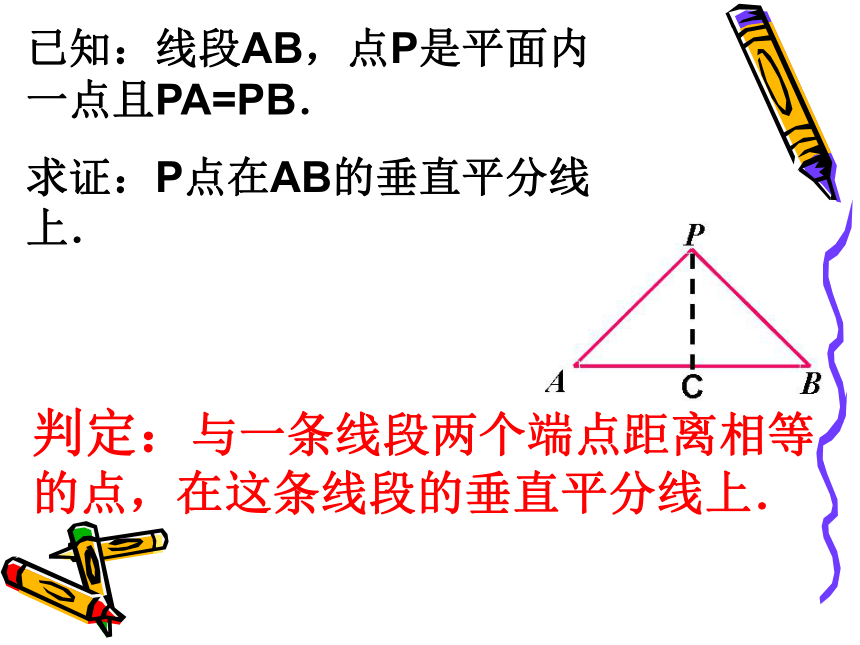
已知:线段AB,点P是平面内 一点且PA=PB.
求证:P点在AB的垂直平分线上.
判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
判定:与一条线段两个端点距离相等的点,在这条
线段的垂直平分线上。
线段的垂直平分线
性质:线段垂直平分线上的点与这条线段两个端
点的距离相等。
PA=PB
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合
任何图形都是有点组成的,因此我们可以把图形看成点的集合。由上述定理和判定,线段的垂直平分线可以看作符合什么条件的点组成的图形?
如图,AD垂直BC,BD=DC,点C在 AE的垂直平分线上,AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?
①
②
③
④
学而不思则罔
1.谈谈本节课你的收获与困惑?
2.你想进一步探究的问题是什么?
___年 ___月___日 星期___ 天气___
学习课题 :
知识归纳与整理:
我的收获与困惑: 自我评价:
悄悄话:老师我想对你说:
学而不厌
阳光套餐
金色套餐:
课本:37页5题,预习第三课时
银色套餐:
课本:38页12题,预习第三课时
谢谢
祝同学们学业有成!
如图,△ABC中,边AB、BC的垂直平分线交于点P。
(1)求证:PA=PB=PC。
(2)点P是否也在边AC的垂直平分线上呢?由此你能得出什么结论?
结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等。
p
·
M
N
A
B
C
E
F
如图:用一根木棒和一根弹性均匀的橡皮筋,做一个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保证射出的箭的方向与木棒垂直呢?为什么?
A
C
B
D
MN是AB的垂直平分线,EF是BC垂直平分线。PA与PC是否相等,为什么?
M
E
P
A
B
C
F
N
如图:AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=________, DA=____.
A
B
E
D
C
4cm
6cm
如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
A
B
C
D
E
(2)
26
给我最大快乐的,
不是已懂的知识,
而是不断的学习. ----高斯
如图,某镇计划在张村和李村之间修一 条笔直的马路,使马路(不考虑路的宽度)上的每一个点与两村的距离都相等,同学们,你们认为应该如何修路呢?
A
张村
李村
1.什么样的图形是轴对称图形?
2.什么叫线段的垂直平分线?
3.线段是不是轴对称图形?如果是,请说出它的对称轴。
A
B
P1
P2
P3
L
如左图,木条L与木条AB钉在一起,L垂直平分AB,P1、P2、P3……是L上的点,分别量一量点P1、P2、P3 ……到A与B的距离,你有什么发现?由此你能得出什么结论?你能用已有的知识来证明吗?
线段垂直平分线上的点与这条线段两个端点距离相等.
已知:如图,MN是AB的垂直平分线, P是MN上任意一点.
求证:PA=PB.
A
C
B
P
M
N
性质:
如图,某镇计划在张村和李村之间修一 条笔直的马路,使马路(不考虑路的宽度)上的每一个点与两村的距离都相等,同学们,你们认为应该如何修路呢?
A
张村
李村
反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
你能给出证明吗?
已知:线段AB,点P是平面内 一点且PA=PB.
求证:P点在AB的垂直平分线上.
判定:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
判定:与一条线段两个端点距离相等的点,在这条
线段的垂直平分线上。
线段的垂直平分线
性质:线段垂直平分线上的点与这条线段两个端
点的距离相等。
PA=PB
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
线段的垂直平分线的集合定义:
线段的垂直平分线可以看作是与线段两个端点距离相等的所有点的集合
任何图形都是有点组成的,因此我们可以把图形看成点的集合。由上述定理和判定,线段的垂直平分线可以看作符合什么条件的点组成的图形?
如图,AD垂直BC,BD=DC,点C在 AE的垂直平分线上,AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?
①
②
③
④
学而不思则罔
1.谈谈本节课你的收获与困惑?
2.你想进一步探究的问题是什么?
___年 ___月___日 星期___ 天气___
学习课题 :
知识归纳与整理:
我的收获与困惑: 自我评价:
悄悄话:老师我想对你说:
学而不厌
阳光套餐
金色套餐:
课本:37页5题,预习第三课时
银色套餐:
课本:38页12题,预习第三课时
谢谢
祝同学们学业有成!
如图,△ABC中,边AB、BC的垂直平分线交于点P。
(1)求证:PA=PB=PC。
(2)点P是否也在边AC的垂直平分线上呢?由此你能得出什么结论?
结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等。
p
·
M
N
A
B
C
E
F
如图:用一根木棒和一根弹性均匀的橡皮筋,做一个简易的“弓”,“箭”通过木棒中央的孔射出去,怎样才能保证射出的箭的方向与木棒垂直呢?为什么?
A
C
B
D
MN是AB的垂直平分线,EF是BC垂直平分线。PA与PC是否相等,为什么?
M
E
P
A
B
C
F
N
如图:AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA=________, DA=____.
A
B
E
D
C
4cm
6cm
如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于D,如果BC=10cm,那么△BCD的周长是_______cm.
A
B
C
D
E
(2)
26
