【2021年高考一轮课程】物理 全国通用版 第12讲 功和功率 动能定理及应用 教案
文档属性
| 名称 | 【2021年高考一轮课程】物理 全国通用版 第12讲 功和功率 动能定理及应用 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 937.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-12 16:24:25 | ||
图片预览



文档简介
2021年高考一轮复习
第十二讲
功和功率
动能定理及应用
教材版本
全国通用
课时说明
120分钟
知识点
1.掌握功和功率及其公式
2.
理解动能定理
3.会应用动能定理进行解题
复习目标
1.熟练掌握功和功率及其公式
2.会求解变力做功,会处理机车启动问题
3.理解动能定理,会应用动能定理进行解题
复习重点
1.利用功和功率的公式进行解题
2.利用动能定理处理问题
复习难点
利用动能定理处理具体问题
一、自我诊断
知己知彼
1.(2020·广东深圳市第一次调研)在水平地面上方某处,把质量相同的P、Q两小球以相同速率沿竖直方向抛出,P向上,Q向下,不计空气阻力,两球从抛出到落地的过程中( )
A.P球重力做功较多
B.两球重力的平均功率相等
C.落地前瞬间,P球重力的瞬时功率较大
D.落地前瞬间,两球重力的瞬时功率相等
【答案】D
【解析】根据W=mgh可知两球重力做功相同,选项A错误;上抛的小球运动时间长,根据P=可知两球重力的平均功率不相等,选项B错误;根据机械能守恒定律mv2=mgh+mv可知,两球落地的速度相同,由P=mgv可知落地前瞬间,两球重力的瞬时功率相等,选项C错误,D正确.
2.(多选)(2019·吉林吉林市友好学校联合体期末)如图1所示,在皮带传送装置中,皮带把物体P匀速带至高处,在此过程中,下述说法正确的是( )
图1
A.摩擦力对物体做正功
B.摩擦力对物体做负功
C.支持力对物体不做功
D.合外力对物体做功为零
【答案】ACD
【解析】取物体为研究对象,受力分析如图所示,受重力mg、沿皮带向上的静摩擦力Ff和垂直于皮带的支持力FN,由于Ff方向与运动方向一致,做正功,A对,B错;FN方向与运动方向垂直,不做功,C对;由于匀速运动,合外力为0,D对.
3.汽车以恒定功率P、初速度v0冲上倾角一定的斜坡时,汽车受到的阻力恒定不变,则汽车上坡过程的v
?t图像不可能是选项图中的( )
【答案】A
【解析】由瞬时功率P=Fv可知,汽车功率恒定,汽车开始所受牵引力F=,若牵引力与汽车所受阻力相等,则汽车做匀速运动,B项中v
?t图像是可能的;若牵引力大于阻力,则汽车做加速运动,则随速度增大,牵引力减小,而汽车所受阻力不变,由牛顿第二定律可知,汽车的加速度减小,直至减小到零,C项中v
?t图像是可能的,A项中v
?t图像是不可能的;若牵引力小于阻力,则汽车做减速运动,牵引力增大,汽车所受阻力不变,由牛顿第二定律可知,汽车的加速度减小,直至减小到零,D项中v
?t图像是可能的。
4.(2020·湖北武汉市调研)一滑块在水平地面上沿直线滑行,t=0时其速度为1
m/s,从此刻开始在滑块运动方向上再施加一水平作用力F,力F、滑块的速率v随时间的变化规律分别如图3甲和乙所示,设在第1
s内、第2
s内、第3
s内力F对滑块做的功分别为W1、W2、W3,则以下关系正确的是( )
图3
A.W1=W2=W3
B.W1C.W1D.W1=W2【答案】B
【解析】在第1
s内,滑块的位移大小为x1=×1×1
m=0.5
m,力F做的功为W1=F1x1=1×0.5
J=0.5
J;第2
s内,滑块的位移大小为x2=×1×1
m=0.5
m,力F做的功为W2=F2x2=3×0.5
J=1.5
J;第3
s内,滑块的位移大小为x3=1×1
m=1
m,力F做的功为W3=F3x3=2×1
J=2
J,所以W15.如图3所示,光滑斜面的顶端固定一弹簧,一小球向右滑行,并冲上固定在地面上的斜面.设小球在斜面最低点A的速度为v,压缩弹簧至C点时弹簧最短,C点距地面高度为h,则小球从A到C的过程中弹簧弹力做功是( )
图3
A.mgh-mv2
B.mv2-mgh
C.-mgh
D.-(mgh+mv2)
【答案】A
【解析】小球从A点运动到C点的过程中,重力和弹簧的弹力对小球做负功,由于支持力与位移始终垂直,则支持力对小球不做功,由动能定理,可得WG+WF=0-mv2,重力做功为WG=-mgh,则弹簧的弹力对小球做功为WF=mgh-mv2,所以正确选项为A.
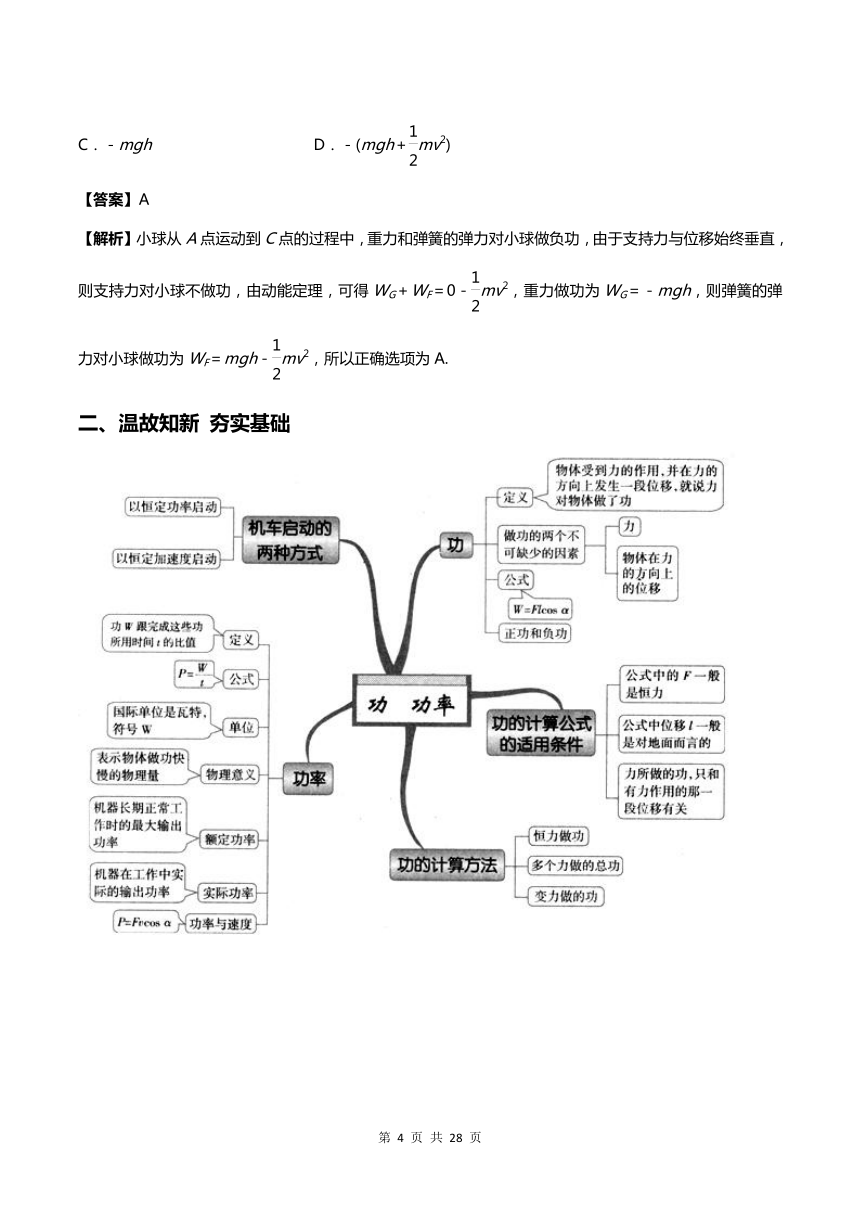
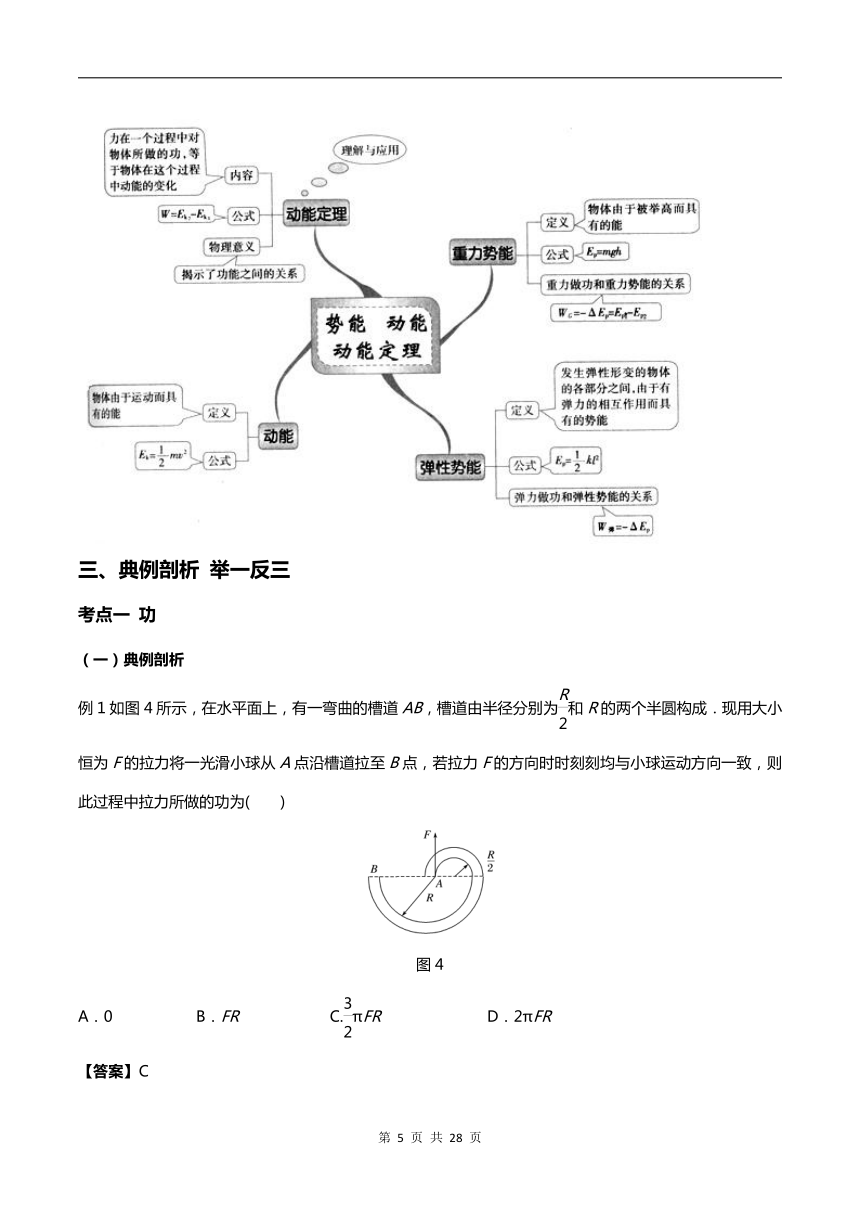
二、温故知新
夯实基础
三、典例剖析
举一反三
考点一
功
(一)典例剖析
例1如图4所示,在水平面上,有一弯曲的槽道AB,槽道由半径分别为和R的两个半圆构成.现用大小恒为F的拉力将一光滑小球从A点沿槽道拉至B点,若拉力F的方向时时刻刻均与小球运动方向一致,则此过程中拉力所做的功为( )
图4
A.0
B.FR
C.πFR
D.2πFR
【答案】C
【解析】虽然拉力方向时刻改变,但力与运动方向始终一致,用微元法,在很小的一段位移内F可以看成恒力,小球的路程为πR+π·,则拉力做的功为πFR,故C正确.
【易错点】没有理解变力做功。
【方法点拨】理解力做功的条件。
例2一物体静止在粗糙水平地面上.现用一大小为F1的水平拉力拉动物体,经过一段时间后其速度变为v.若将水平拉力的大小改为F2,物体从静止开始经过同样的时间后速度变为2v.对于上述两个过程,用WF1、WF2分别表示拉力F1、F2所做的功,Wf1、Wf2分别表示前后两次克服摩擦力所做的功,则( )
A.WF2>4WF1,Wf2>2Wf1
B.WF2>4WF1,Wf2=2Wf1
C.WF2<4WF1,Wf2=2Wf1
D.WF2<4WF1,Wf2<2Wf1
【答案】C
【解析】根据x=t得,两过程的位移关系x1=x2,根据加速度的定义a=,得两过程的加速度关系为a1=.由于在相同的粗糙水平地面上运动,故两过程的摩擦力大小相等,即Ff1=Ff2=Ff,根据牛顿第二定律得,F1-Ff1=ma1,F2-Ff2=ma2,所以F1=F2+Ff,即F1>.根据功的计算公式W=Fl,可知Wf1=Wf2,WF1>WF2,故选项C正确,选项A、B、D错误.
【易错点】误以为当合力是1:2时,外力也是1:2的关系。
【方法点拨】本题应根据牛顿第二定律解出两种情况下外力的关系,再算出位移的关系,从而比较做工的大小。
例3轻质弹簧右端固定在墙上,左端与一质量m=0.5
kg的物块相连,如图5甲所示,弹簧处于原长状态,物块静止且与水平面间的动摩擦因数μ=0.2.以物块所在处为原点,水平向右为正方向建立x轴,现对物块施加水平向右的外力F,F随x轴坐标变化的情况如图乙所示,物块运动至x=0.4
m处时速度为零,则此时弹簧的弹性势能为(g=10
m/s2)( )
图5
A.3.1
J
B.3.5
J
C.1.8
J
D.2.0
J
【答案】A
【解析】物块与水平面间的摩擦力大小为Ff=μmg=1
N.现对物块施加水平向右的外力F,由F-x图象与x轴所围面积表示功,可知F做功W=3.5
J,克服摩擦力做功Wf=Ffx=0.4
J.由于物块运动至x=0.4
m处时,速度为0,由功能关系可知,W-Wf=Ep,此时弹簧的弹性势能为Ep=3.1
J,选项A正确.
【易错点】不会分析变力做功
【方法点拨】准确进行受力分析,运动状态分析,会判断变力做功。
(二)举一反三
1.
(2019·广东珠海市质量监测)如图6所示,质量均为m的木块A和B,用一个劲度系数为k的竖直轻质弹簧连接,最初系统静止,重力加速度为g,现在用力F向上缓慢拉A直到B刚好要离开地面,则这一过程中力F做的功至少为( )
图6
A.
B.
C.
D.
【答案】B
【解析】开始时,A、B都处于静止状态,弹簧的压缩量设为x1,由胡克定律有kx1=mg;木块B恰好离开地面时,弹簧的拉力等于B的重力,设此时弹簧的伸长量为x2,由胡克定律有kx2=mg,可得x1=x2=,则这一过程中,弹簧弹力做功为零,木块A上升的高度h=x1+x2=,设变力F做的功为WF,由动能定理得WF-WG=0,又WG=mgh=,所以WF=,B选项正确.
2.(多选)
用起重机提升货物,货物上升过程中的vt图象如图7所示,在t=3
s到t=5
s内,重力对货物做的功为W1、绳索拉力对货物做的功为W2、货物所受合力做的功为W3,则( ).
图7
A.W1>0
B.W2<0
C.W2>0
D.W3<0
【答案】CD
【解析】分析题图可知,货物一直向上运动,根据功的定义式可得:重力做负功,拉力做正功,即W1<0,W2>0,A、B错误,C正确;根据动能定理:合力做的功W3=0-mv2,v=2
m/s,即W3<0,D正确.
3.
(2020·安徽安庆市模拟)如图8所示,固定的光滑竖直杆上套着一个滑块,滑块用轻绳系着绕过光滑的定滑轮O.现以大小不变的拉力F拉绳,使滑块从A点起由静止开始上升.滑块运动到C点时速度最大.已知滑块质量为m,滑轮O到竖直杆的距离为d,∠OAO′=37°,∠OCO′=53°,重力加速度为g.求:(sin
37°=0.6,cos
37°=0.8)
图8
(1)拉力F的大小;
(2)滑块由A到C过程中拉力F做的功.
【答案】(1)mg (2)mgd
【解析】(1)滑块运动到C点时速度最大,则在C点有
Fcos
53°=mg
解得F=mg.
(2)由能量守恒可知,拉力F对绳端点做的功就等于绳的拉力F对滑块做的功.
滑轮与A间绳长L1=
滑轮与C间绳长L2=
则滑轮右侧绳子增加的长度
ΔL=L1-L2=-=
故拉力做的功W=FΔL=mgd.
考点二
功率
机车启动
(一)典例剖析
例1某大瀑布的平均水流量为,水的落差为。已知水的密度为。在大瀑布水流下落过程中,重力做功的平均功率约为
(
)
A.
B.
C.
D.
【答案】D
【解析】每秒钟水流的质量为,重力做功的平均功率约为,选项D正确。
【易错点】没有真正理解平均功率的公式。
【方法点拨】理解瞬时功率和平均功率公式和区别是解题的关键。
例2(多选)(2019·江苏苏州市调研)质量为2×103
kg的汽车由静止开始沿平直公路行驶,行驶过程中牵引力F和车速倒数的关系图象如图8所示.已知行驶过程中最大车速为30
m/s,设阻力恒定,则( )
图8
A.汽车所受阻力为6×103
N
B.汽车在车速为5
m/s时,加速度为3
m/s2
C.汽车在车速为15
m/s时,加速度为1
m/s2
D.汽车在行驶过程中的最大功率为6×104
W
【答案】CD
【解析】当牵引力等于阻力时,速度最大,由题图可知阻力大小Ff=2
000
N,故A错误;车速为5
m/s时,汽车的加速度a=
m/s2=2
m/s2,故B错误;题中倾斜图线的斜率表示汽车的额定功率,可知P=Ffv=2
000×30
W=6×104
W,当车速为15
m/s时,牵引力F==
N=4
000
N,则加速度a′==
m/s2=1
m/s2,故C正确;汽车的最大功率等于额定功率,等于6×104
W,故D正确.
【易错点】不能正确运用图象。
【方法点拨】充分利用图象,找出图象中的有效信息。
例3汽车在平直公路上以速度v0匀速行驶,发动机功率为P.快进入闹区时,司机减小了油门,使汽车的功率立即减小一半并保持该功率继续行驶.下面四个图象中,哪个图象正确表示了从司机减小油门开始,汽车的速度与时间的关系( )
【答案】C
【解析】功率减小一半时,由于惯性汽车速度来不及变化,根据功率和速度关系公式P=Fv,此时牵引力减小一半,小于阻力,汽车做减速运动,由公式P=Fv可知,功率一定时,速度减小后,牵引力增大,合力减小,加速度减小,故汽车做加速度越来越小的减速运动,当牵引力增大到等于阻力时,汽车做匀速运动,C正确.
【易错点】误认为功率变化的瞬间速度会突变。
【方法点拨】当功率变化的瞬间牵引力会发生突变,从而引起加速度的变化,最终导致了速度的变化。
(二)举一反三
1.
把A、B两相同小球在离地面同一高度处以相同大小的初速度v0分别沿水平方向和竖直方向抛出,不计空气阻力,如图10所示,则下列说法正确的是( )
图10
A.两小球落地时速度相同
B.两小球落地时,重力的瞬时功率相同
C.从开始运动至落地,重力对两小球做的功相同
D.从开始运动至落地,重力对两小球做功的平均功率相同
【答案】C
【解析】A、B两球落地的速度大小相同,方向不同,A错误;由P=mg·v竖可知,因B球落地时竖直速度较大,故PB>PA,B错误;重力做功与路径无关,均为mgh,C正确;因B球从抛出到落地所用时间较长,故A>B,D错误。
2.
(多选)一质量为1
kg的质点静止于光滑水平面上,从t=0时刻开始,受到水平外力F作用,如图11所示.下列判断正确的是( )
图11
A.0~2
s内外力的平均功率是4
W
B.第2
s内外力所做的功是4
J
C.第2
s末外力的瞬时功率最大
D.第1
s末与第2
s末外力的瞬时功率之比为9∶4
【答案】AD
【解析】第1
s末质点的速度
v1=t1=×1
m/s=3
m/s.
第2
s末质点的速度
v2=v1+t2=(3+×1)
m/s=4
m/s.
则第2
s内外力做功W2=mv-mv=3.5
J
0~2
s内外力的平均功率
P==
W=4
W.
选项A正确,选项B错误;
第1
s末外力的瞬时功率P1=F1v1=3×3
W=9
W,
第2
s末外力的瞬时功率P2=F2v2=1×4
W=4
W,故
P1∶P2=9∶4.选项C错误,选项D正确.
3.
一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数的关系图像如图12所示。若已知汽车的质量,则根据图像所给的信息,不能求出的物理量是( )
图12
A.汽车的功率
B.汽车行驶的最大速度
C.汽车所受到的阻力
D.汽车运动到最大速度所需的时间
【答案】D
【解析】由F-Ff=ma,P=Fv可得:a=·-,对应图线可知,=k=40,可求出汽车的功率P,由a=0时,=0.05可得:vm=20
m/s,再由vm=,可求出汽车受到的阻力Ff,但无法求出汽车运动到最大速度所需的时间。
考点三
动能定理及其应用
(一)典例剖析
例1如图13所示,AB为圆弧轨道,BC为水平直轨道,BC恰好在B点与AB相切,圆弧的半径为R,BC的长度也是R.一质量为m的物体与两个轨道间的动摩擦因数都为μ,它由轨道顶端A从静止开始下落,恰好运动到C处停止,重力加速度为g,那么物体在AB段克服摩擦力所做的功为( )
图13
A.
B.
C.mgR
D.(1-μ)mgR
【答案】D
【解析】设物体在AB段克服摩擦力所做的功为WAB,物体从A到C的全过程,根据动能定理有mgR-WAB-μmgR=0,所以WAB=mgR-μmgR=(1-μ)mgR,故D正确.
【易错点】不能正确写出动能定理的表达式。
【方法点拨】对整个过程进行分析,列出动能定理表达式进行求解。
例2(多选)如图14所示,一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的外力拉B,由于A、B间摩擦力的作用,A将在B上滑动,以地面为参考系,A、B都向前移动了一段距离.在此过程中( )
图14
A.外力F做的功等于A和B动能的增量
B.B对A的摩擦力所做的功等于A的动能的增量
C.A对B的摩擦力所做的功等于B对A的摩擦力所做的功
D.外力F对B做的功等于B的动能的增量与B克服摩擦力所做的功之和
【答案】BD
【解析】A物体所受的合外力等于B对A的摩擦力,对A物体运用动能定理,则有B对A的摩擦力所做的功等于A的动能的增量,B正确;A对B的摩擦力与B对A的摩擦力是一对作用力与反作用力,大小相等,方向相反,但是由于A在B上滑动,A、B相对地面的位移不相等,故二者做功不相等,C错误;对B应用动能定理WF-Wf=ΔEkB,则WF=ΔEkB+Wf,即外力F对B做的功等于B的动能的增量与B克服摩擦力所做的功之和,D正确;根据功能关系可知,外力F做的功等于A和B动能的增量与产生的内能之和,故A错误.
【易错点】不能区分各摩擦力的做功的问题。
【方法点拨】区分各摩擦力做功。
例3如图15所示,用一块长L1=1.0
m的木板在墙和桌面间架设斜面,桌子高H=0.8
m,长L2=1.5
m.斜面与水平桌面的夹角θ可在0~60°间调节后固定.将质量m=0.2
kg的小物块从斜面顶端静止释放,物块与斜面间的动摩擦因数μ1=0.05,物块与桌面间的动摩擦因数为μ2,忽略物块在斜面与桌面交接处的能量损失.(重力加速度取g=10
m/s2;最大静摩擦力等于滑动摩擦力)
图15
(1)求θ角增大到多少时,物块能从斜面开始下滑;(用正切值表示)
(2)当θ角增大到37°时,物块恰能停在桌面边缘,求物块与桌面间的动摩擦因数μ2;(已知sin
37°=0.6,cos
37°=0.8)
(3)继续增大θ角,发现θ=53°时物块落地点与墙面的距离最大,求此最大距离xm.
【答案】(1)arctan
0.05 (2)0.8 (3)1.9
m
【解析】(1)为使小物块下滑,应有mgsin
θ≥μ1mgcos
θ①
θ满足的条件tan
θ≥0.05②
即当θ=arctan
0.05时物块恰好从斜面开始下滑.
(2)克服摩擦力做功Wf=μ1mgL1cos
θ+μ2mg(L2-L1cos
θ)③
由动能定理得mgL1sin
θ-Wf=0④
代入数据得μ2=0.8⑤
(3)由动能定理得mgL1sin
θ-Wf=mv2⑥
结合③式并代入数据得v=1
m/s⑦
由平抛运动规律得H=gt2,x1=vt
解得t=0.4
s⑧
x1=0.4
m⑨
xm=x1+L2=1.9
m
【易错点】不能准确的分析出物体的整个运动过程
【方法点拨】进行物理模型的分解,对每个模型进行单独分析,并找出模型间的相关联的物理量。
(二)举一反三
1.
(多选)质量不等,但有相同动能的两个物体,在动摩擦因数相同的水平地面上滑行,直至停止,则( ).
A.质量大的物体滑行的距离大
B.质量小的物体滑行的距离大
C.它们滑行的距离一样大
D.它们克服摩擦力所做的功一样多
【答案】BD
【解析】由动能定理可得-Ffx=0-Ek,即μmgx=Ek,由于动能相同动摩擦因数相同,故质量小的滑行距离大,它们克服摩擦力所做的功都等于Ek.
2.
(2018·全国卷Ⅱ)如图16,某同学用绳子拉动木箱,使它从静止开始沿粗糙水平路面运动至具有某一速度.木箱获得的动能一定( )
图16
A.小于拉力所做的功
B.等于拉力所做的功
C.等于克服摩擦力所做的功
D.大于克服摩擦力所做的功
【答案】A
【解析】由题意知,W拉-W克摩=ΔEk,则W拉>ΔEk,A项正确,B项错误;W克摩与ΔEk的大小关系不确定,C、D项错误.
3.
如图17甲所示,轻弹簧左端固定在竖直墙上,右端点在O位置.质量为m的物块A(可视为质点)以初速度v0从距O点右方x0的P点处向左运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回.A离开弹簧后,恰好回到P点.物块A与水平面间的动摩擦因数为μ.求:
图17
(1)物块A从P点出发又回到P点的过程,克服摩擦力所做的功.
(2)O点和O′点间的距离x1.
(3)如图乙所示,若将另一个与A完全相同的物块B(可视为质点)与弹簧右端拴接,将A放在B右边,向左推A、B,使弹簧右端压缩到O′点位置,然后从静止释放,A、B共同滑行一段距离后分离.分离后物块A向右滑行的最大距离x2是多少?
【答案】(1)mv (2)-x0 (3)x0-
【解析】(1)物块A从P点出发又回到P点的过程,根据动能定理得克服摩擦力所做的功为Wf=mv.
(2)物块A从P点出发又回到P点的过程,根据动能定理得2μmg(x1+x0)=mv
解得x1=-x0
(3)A、B在弹簧处于原长处分离,设此时它们的共同速度是v1,弹出过程弹力做功WF
只有A时,从O′到P有WF-μmg(x1+x0)=0-0
A、B共同从O′到O有WF-2μmgx1=×2mv
分离后对A有mv=μmgx2
联立以上各式可得x2=x0-.
四、分层训练
能力进阶
【基础】
1.
(多选)
(2019·宁夏银川市质检)如图18所示为一滑草场.某条滑道由上下两段高均为h,与水平面倾角分别为45°和37°的滑道组成,载人滑草车与草地之间的动摩擦因数为μ.质量为m的载人滑草车从坡顶由静止开始自由下滑,经过上、下两段滑道后,最后恰好静止于滑道的底端(不计载人滑草车在两段滑道交接处的能量损失,重力加速度为g,sin
37°=0.6,cos
37°=0.8).则( )
图18
A.动摩擦因数μ=
B.载人滑草车最大速度为
C.载人滑草车克服摩擦力做功为mgh
D.载人滑草车在下段滑道上的加速度大小为g
【答案】AB
【解析】对载人滑草车从坡顶由静止开始滑到底端的全过程分析,由动能定理可知:mg·2h-μmgcos
45°·-μmgcos
37°·=0,解得μ=,选项A正确;
对经过上段滑道的过程分析,根据动能定理有mgh-μmgcos
45°·=mv,解得:vm=,选项B正确;载人滑草车克服摩擦力做功为2mgh,选项C错误;载人滑草车在下段滑道上的加速度为a==-g,故大小为g,选项D错误.
2.如图19所示,质量为m的小球以初速度v0水平抛出,恰好垂直打在倾角为θ的斜面上,则小球落在斜面上时重力的瞬时功率为(不计空气阻力)( )
图19
A.mgv0tan
θ
B.
C.
D.mgv0cos
θ
【答案】B
【解析】小球落在斜面上时重力的瞬时功率为P=mgvy,而vytan
θ=v0,所以P=,B正确。
2.
(2019·安徽合肥市第二次质检)如图20甲所示,置于水平地面上质量为m的物体,在竖直拉力F作用下,由静止开始向上运动,其动能Ek与距地面高度h的关系图象如图乙所示,已知重力加速度为g,空气阻力不计.下列说法正确的是( )
图20
A.在0~h0过程中,F大小始终为mg
B.在0~h0和h0~2h0过程中,F做功之比为2∶1
C.在0~2h0过程中,物体的机械能不断增加
D.在2h0~3.5h0过程中,物体的机械能不断减少
【答案】C
【解析】0~h0过程中,Ek-h图象为一段直线,由动能定理得:(F-mg)h0=mgh0-0,故F=2mg,A错误;由A可知,在0~h0过程中,F做功为2mgh0,在h0~2h0过程中,由动能定理可知,WF-mgh0=1.5mgh0-mgh0,解得WF=1.5mgh0,因此在0~h0和h0~2h0过程中,F做功之比为4∶3,故B错误;在0~2h0过程中,F一直做正功,故物体的机械能不断增加,C正确;在2h0~3.5h0过程中,由动能定理得WF′-1.5mgh0=0-1.5mgh0,则WF′=0,故F做功为0,物体的机械能保持不变,故D错误.
3.
如图21所示,演员正在进行杂技表演。由图可估算出他将一只鸡蛋抛出的过程中对鸡蛋所做的功最接近于(
)
图21
A.0.3J
B.3J
C.30J
D.300J
【答案】A
【解析】生活经验告诉我们:10个鸡蛋大约1斤即0.5kg,则一个鸡蛋的质量约为,鸡蛋大约能抛高度h=0.6m,则做功约为W=mgh=0.05×10×0.6J=0.3J,A正确。
4.
在离地面高为h处竖直上抛一质量为m的物块,抛出时的速度为v0,它落到地面时的速度为v,用g表示重力加速度,则在此过程中物块克服空气阻力所做的功等于( )
A.mgh-mv2-mv
B.-mv2-mv-mgh
C.mgh+mv-mv2
D.mgh+mv2-mv
【答案】C
【解析】对物块从h高处竖直上抛到落地的过程,根据动能定理可得mgh-Wf=mv2-mv,解得Wf=mgh+mv-mv2,选项C正确.
5.
一个25
kg的小孩从高度为3.0
m的滑梯顶端由静止开始滑下,滑到底端时的速度为2.0
m/s.取g=10
m/s2,关于力对小孩做的功,以下结果正确的是( ).
A.合外力做功50
J
B.阻力做功500
J
C.重力做功500
J
D.支持力做功50
J
【答案】A
【解析】合外力做的功W合=Ek-0,即W合=mv2=×25×22
J=50
J,A项正确;WG+W阻=Ek-0,故W阻=mv2-mgh=50
J-750
J=-700
J,B项错误;重力做功WG=mgh=25×10×3
J=750
J,C错;小孩所受支持力方向上的位移为零,故支持力做的功为零,D错.
【巩固】
1.
(多选)
(2020·山西运城市质检)质量为m的物体放在水平面上,它与水平面间的动摩擦因数为μ,重力加速度为g.用水平力拉物体,运动一段时间后撤去此力,最终物体停止运动.物体运动的v-t图象如图22所示.下列说法正确的是( )
图22
A.水平拉力大小为F=m
B.物体在0~3t0时间内的位移大小为v0t0
C.在0~3t0时间内水平拉力做的功为mv
D.在0~3t0时间内物体克服摩擦力做功的平均功率为μmgv0
【答案】BD
【解析】根据v-t图象和牛顿第二定律可知F-μmg=m,故选项A错误;由v-t图象与t坐标轴所围面积表示位移可知,在0~3t0时间内的位移大小为x=·3t0·v0=v0t0,所以选项B正确;在0~3t0时间内由动能定理可知W-μmgx=0,故水平拉力做的功W=μmgv0t0,又Ff=μmg=,则W=mv,选项C错误;在0~3t0时间内物体克服摩擦力做功的平均功率为===μmgv0,所以选项D正确.
2.一个质量为m的小球做自由落体运动,那么,在前t秒内重力对它做功的平均功率及在t秒末重力做功的瞬时功率P分别为( )
A.=mg2t2,P=mg2t2
B.=mg2t2,P=mg2t2
C.=mg2t,P=mg2t
D.=mg2t,P=2mg2t
【答案】C
【解析】前t秒内重力做功的平均功率===mg2t;t秒末重力做功的瞬时功率P=Fv=mg·gt=mg2t,故C正确.
3.
如图23是质量为1
kg的质点在水平面上运动的v-t图象,以水平向右的方向为正方向.以下判断正确的是( )
图23
A.在0~3.0
s时间内,合力对质点做功为10
J
B.在4.0~6.0
s时间内,质点的平均速度为3
m/s
C.在1.0~5.0
s时间内,合力的平均功率为4
W
D.在t=6.0
s时,质点的加速度为零
【答案】B
【解析】在0~3.0
s时间内,由动能定理W合=ΔEk=6
J,所以A错误.在4.0~6.0
s时间内,由图象可知s=6
m,==3
m/s,所以B正确.在1.0~5.0
s时间内,W合=ΔEk=8
J,==2
W,C错误.由题图可知,t=6.0
s时质点的加速度a=-4
m/s2,D错误.
4.
某汽车以额定功率在水平路面上行驶,空载时的最大速度为v1,装满货物后的最大速度为v2,已知汽车空车的质量为m0,汽车所受的阻力跟车重成正比,则汽车后来所装货物的质量是( )
A.m0
B.m0
C.m0
D.m0
【答案】A
【解析】当汽车空载时,有:P=Ff1v1=km0gv1,当汽车装满货物后,有:P=Ff2v2=k(m0+m)gv2
联立两式解得:m=m0.故A正确,B、C、D错误.
5.
用铁锤把小铁钉钉入木板,设木板对钉子的阻力与钉进木板的深度成正比,已知铁锤第一次将钉子钉进d,如果铁锤第二次敲钉子时对钉子做的功与第一次相同,那么,第二次钉子进入木板的深度是( )
A.(-1)
d
B.(-1)d
C.d
D.d
【答案】B
【解析】在将钉子钉入木板的过程中,随着深度的增加,阻力成正比地增加,这属于变力做功问题,由于力与位移成正比,可求出力对位移的平均值,将变力转化为恒力来处理.
根据题意可得
第一次做功:W=F1d=d.
第二次做功:W=F2d′=d′.
联立解得d′=(-1)d.
【拔高】
1.
(多选)
我国科学家正在研制航母舰载机使用的电磁弹射器.舰载机总质量为3.0×104
kg,设起飞过程中发动机的推力恒为1.0×105
N;弹射器有效作用长度为100
m,推力恒定.要求舰载机在水平弹射结束时速度大小达到80
m/s.弹射过程中舰载机所受总推力为弹射器和发动机推力之和,假设所受阻力为总推力的20%,则( )
A.弹射器的推力大小为1.1×106
N
B.弹射器对舰载机所做的功为1.1×108
J
C.弹射器对舰载机做功的平均功率为8.8×107
W
D.舰载机在弹射过程中的加速度大小为32
m/s2
【答案】ABD
【解析】设总推力为F,位移x=100
m,阻力F阻=20%F,对舰载机加速过程由动能定理得Fx-20%F·x=mv2,解得F=1.2×106
N,弹射器推力F弹=F-F发=1.2×106
N-1.0×105
N=1.1×106
N,A正确;弹射器对舰载机所做的功为W=F弹·x=1.1×106×100
J=1.1×108
J,B正确;弹射器对舰载机做功的平均功率=F弹·=4.4×107
W,C错误;根据运动学公式v2=2ax,得a==32
m/s2,D正确.
2.
在地面上某处将一金属小球竖直向上拋出,上升一定高度后再落回原处,若不考虑空气阻力,则下列图象能正确反映小球的速度、加速度、位移和动能随时间变化关系的是(取向上为正方向)( )
【答案】A
【解析】小球运动过程中加速度不变,B错;速度均匀变化先减小后反向增大,A对;位移和动能与时间不是线性关系,C、D错.
3.(2020年全国II卷)如图24所示,在摩托车越野赛途中的水平路段前方有一个坑,该坑沿摩托车前进方向的水平宽度为3h,其左边缘a点比右边缘b点高0.5h.若摩托车经过a点时的动能为E1,它会落到坑内c点.c与a的水平距离和高度差均为h;若经过a点时的动能为E2,该摩托车恰能越过坑到达b点.等于(
)
A.20
B.18
C.9.0
D.3.0
【答案】B
【解析】由题意可知两次平抛运动的竖直位移之比为2:1,水平位移之比为1:3,根据,x=v0t可得,,由可得,所以B正确。
4.(2019·河南平顶山市一轮复习质检)如图25所示,半径为r的半圆弧轨道ABC固定在竖直平面内,直径AC水平,一个质量为m的物块从圆弧轨道A端正上方P点由静止释放,物块刚好从A点无碰撞地进入圆弧轨道并做匀速圆周运动,到B点时对轨道的压力大小等于物块重力的2倍,重力加速度为g,不计空气阻力,不计物块的大小,则:
图25
(1)物块到达A点时的速度大小和PA间的高度差分别为多少?
(2)物块从A运动到B所用时间和克服摩擦力做的功分别为多少?
【答案】(1) (2) mgr
【解析】(1)设物块在B点时的速度为v,由牛顿第二定律得:FN-mg=m,
因为FN=2mg,所以v=,
因为物块从A点进入圆弧轨道并做匀速圆周运动,所以物块到达A点时速度大小为;
设PA间的高度差为h,从P到A的过程由动能定理得:mgh=mv2,所以h=.
(2)因为物块从A点进入圆弧轨道并做匀速圆周运动,所以物块从A运动到B所用时间t==;
从A运动到B由动能定理有:mgr-W克f=0,解得:W克f=mgr.
5.
(2019·河南名校联盟高三下学期联考)如图26所示,AB是一段位于竖直平面内的光滑轨道,高度为h,末端B处的切线方向水平.一个质量为m的小物体P从轨道顶端A处由静止释放,滑到B端后飞出,落到地面上的C点,轨迹如图中虚线BC所示.已知它落地时相对于B点的水平位移OC
=
l.现在轨道下方紧贴B点安装一水平木板,木板的右端与B的距离为,让P再次从A点由静止释放,它离开轨道并在木板上滑行后从右端水平飞出,仍然落在地面的C点.求:(不计空气阻力,重力加速度为g)
图26
(1)P滑至B点时的速度大小;
(2)P与木板之间的动摩擦因数μ.
【答案】(1) (2)
【解析】(1)物体P在AB轨道上滑动时,根据动能定理mgh=mv
得物体P滑到B点时的速度大小为v0=
(2)当没有木板时,物体离开B点后做平抛运动,设运动时间为t,有:
t==
当在轨道下方紧贴B点安装木板时,物体从木板右端水平抛出,在空中运动的时间也为t,水平位移为,因此物体从木板右端抛出的速度v1==
根据动能定理,物体在木板上滑动时,有
-μmg=mv-mv
解得物体P与木板之间的动摩擦因数μ=.
第十二讲
功和功率
动能定理及应用
教材版本
全国通用
课时说明
120分钟
知识点
1.掌握功和功率及其公式
2.
理解动能定理
3.会应用动能定理进行解题
复习目标
1.熟练掌握功和功率及其公式
2.会求解变力做功,会处理机车启动问题
3.理解动能定理,会应用动能定理进行解题
复习重点
1.利用功和功率的公式进行解题
2.利用动能定理处理问题
复习难点
利用动能定理处理具体问题
一、自我诊断
知己知彼
1.(2020·广东深圳市第一次调研)在水平地面上方某处,把质量相同的P、Q两小球以相同速率沿竖直方向抛出,P向上,Q向下,不计空气阻力,两球从抛出到落地的过程中( )
A.P球重力做功较多
B.两球重力的平均功率相等
C.落地前瞬间,P球重力的瞬时功率较大
D.落地前瞬间,两球重力的瞬时功率相等
【答案】D
【解析】根据W=mgh可知两球重力做功相同,选项A错误;上抛的小球运动时间长,根据P=可知两球重力的平均功率不相等,选项B错误;根据机械能守恒定律mv2=mgh+mv可知,两球落地的速度相同,由P=mgv可知落地前瞬间,两球重力的瞬时功率相等,选项C错误,D正确.
2.(多选)(2019·吉林吉林市友好学校联合体期末)如图1所示,在皮带传送装置中,皮带把物体P匀速带至高处,在此过程中,下述说法正确的是( )
图1
A.摩擦力对物体做正功
B.摩擦力对物体做负功
C.支持力对物体不做功
D.合外力对物体做功为零
【答案】ACD
【解析】取物体为研究对象,受力分析如图所示,受重力mg、沿皮带向上的静摩擦力Ff和垂直于皮带的支持力FN,由于Ff方向与运动方向一致,做正功,A对,B错;FN方向与运动方向垂直,不做功,C对;由于匀速运动,合外力为0,D对.
3.汽车以恒定功率P、初速度v0冲上倾角一定的斜坡时,汽车受到的阻力恒定不变,则汽车上坡过程的v
?t图像不可能是选项图中的( )
【答案】A
【解析】由瞬时功率P=Fv可知,汽车功率恒定,汽车开始所受牵引力F=,若牵引力与汽车所受阻力相等,则汽车做匀速运动,B项中v
?t图像是可能的;若牵引力大于阻力,则汽车做加速运动,则随速度增大,牵引力减小,而汽车所受阻力不变,由牛顿第二定律可知,汽车的加速度减小,直至减小到零,C项中v
?t图像是可能的,A项中v
?t图像是不可能的;若牵引力小于阻力,则汽车做减速运动,牵引力增大,汽车所受阻力不变,由牛顿第二定律可知,汽车的加速度减小,直至减小到零,D项中v
?t图像是可能的。
4.(2020·湖北武汉市调研)一滑块在水平地面上沿直线滑行,t=0时其速度为1
m/s,从此刻开始在滑块运动方向上再施加一水平作用力F,力F、滑块的速率v随时间的变化规律分别如图3甲和乙所示,设在第1
s内、第2
s内、第3
s内力F对滑块做的功分别为W1、W2、W3,则以下关系正确的是( )
图3
A.W1=W2=W3
B.W1
【解析】在第1
s内,滑块的位移大小为x1=×1×1
m=0.5
m,力F做的功为W1=F1x1=1×0.5
J=0.5
J;第2
s内,滑块的位移大小为x2=×1×1
m=0.5
m,力F做的功为W2=F2x2=3×0.5
J=1.5
J;第3
s内,滑块的位移大小为x3=1×1
m=1
m,力F做的功为W3=F3x3=2×1
J=2
J,所以W1
图3
A.mgh-mv2
B.mv2-mgh
C.-mgh
D.-(mgh+mv2)
【答案】A
【解析】小球从A点运动到C点的过程中,重力和弹簧的弹力对小球做负功,由于支持力与位移始终垂直,则支持力对小球不做功,由动能定理,可得WG+WF=0-mv2,重力做功为WG=-mgh,则弹簧的弹力对小球做功为WF=mgh-mv2,所以正确选项为A.
二、温故知新
夯实基础
三、典例剖析
举一反三
考点一
功
(一)典例剖析
例1如图4所示,在水平面上,有一弯曲的槽道AB,槽道由半径分别为和R的两个半圆构成.现用大小恒为F的拉力将一光滑小球从A点沿槽道拉至B点,若拉力F的方向时时刻刻均与小球运动方向一致,则此过程中拉力所做的功为( )
图4
A.0
B.FR
C.πFR
D.2πFR
【答案】C
【解析】虽然拉力方向时刻改变,但力与运动方向始终一致,用微元法,在很小的一段位移内F可以看成恒力,小球的路程为πR+π·,则拉力做的功为πFR,故C正确.
【易错点】没有理解变力做功。
【方法点拨】理解力做功的条件。
例2一物体静止在粗糙水平地面上.现用一大小为F1的水平拉力拉动物体,经过一段时间后其速度变为v.若将水平拉力的大小改为F2,物体从静止开始经过同样的时间后速度变为2v.对于上述两个过程,用WF1、WF2分别表示拉力F1、F2所做的功,Wf1、Wf2分别表示前后两次克服摩擦力所做的功,则( )
A.WF2>4WF1,Wf2>2Wf1
B.WF2>4WF1,Wf2=2Wf1
C.WF2<4WF1,Wf2=2Wf1
D.WF2<4WF1,Wf2<2Wf1
【答案】C
【解析】根据x=t得,两过程的位移关系x1=x2,根据加速度的定义a=,得两过程的加速度关系为a1=.由于在相同的粗糙水平地面上运动,故两过程的摩擦力大小相等,即Ff1=Ff2=Ff,根据牛顿第二定律得,F1-Ff1=ma1,F2-Ff2=ma2,所以F1=F2+Ff,即F1>.根据功的计算公式W=Fl,可知Wf1=Wf2,WF1>WF2,故选项C正确,选项A、B、D错误.
【易错点】误以为当合力是1:2时,外力也是1:2的关系。
【方法点拨】本题应根据牛顿第二定律解出两种情况下外力的关系,再算出位移的关系,从而比较做工的大小。
例3轻质弹簧右端固定在墙上,左端与一质量m=0.5
kg的物块相连,如图5甲所示,弹簧处于原长状态,物块静止且与水平面间的动摩擦因数μ=0.2.以物块所在处为原点,水平向右为正方向建立x轴,现对物块施加水平向右的外力F,F随x轴坐标变化的情况如图乙所示,物块运动至x=0.4
m处时速度为零,则此时弹簧的弹性势能为(g=10
m/s2)( )
图5
A.3.1
J
B.3.5
J
C.1.8
J
D.2.0
J
【答案】A
【解析】物块与水平面间的摩擦力大小为Ff=μmg=1
N.现对物块施加水平向右的外力F,由F-x图象与x轴所围面积表示功,可知F做功W=3.5
J,克服摩擦力做功Wf=Ffx=0.4
J.由于物块运动至x=0.4
m处时,速度为0,由功能关系可知,W-Wf=Ep,此时弹簧的弹性势能为Ep=3.1
J,选项A正确.
【易错点】不会分析变力做功
【方法点拨】准确进行受力分析,运动状态分析,会判断变力做功。
(二)举一反三
1.
(2019·广东珠海市质量监测)如图6所示,质量均为m的木块A和B,用一个劲度系数为k的竖直轻质弹簧连接,最初系统静止,重力加速度为g,现在用力F向上缓慢拉A直到B刚好要离开地面,则这一过程中力F做的功至少为( )
图6
A.
B.
C.
D.
【答案】B
【解析】开始时,A、B都处于静止状态,弹簧的压缩量设为x1,由胡克定律有kx1=mg;木块B恰好离开地面时,弹簧的拉力等于B的重力,设此时弹簧的伸长量为x2,由胡克定律有kx2=mg,可得x1=x2=,则这一过程中,弹簧弹力做功为零,木块A上升的高度h=x1+x2=,设变力F做的功为WF,由动能定理得WF-WG=0,又WG=mgh=,所以WF=,B选项正确.
2.(多选)
用起重机提升货物,货物上升过程中的vt图象如图7所示,在t=3
s到t=5
s内,重力对货物做的功为W1、绳索拉力对货物做的功为W2、货物所受合力做的功为W3,则( ).
图7
A.W1>0
B.W2<0
C.W2>0
D.W3<0
【答案】CD
【解析】分析题图可知,货物一直向上运动,根据功的定义式可得:重力做负功,拉力做正功,即W1<0,W2>0,A、B错误,C正确;根据动能定理:合力做的功W3=0-mv2,v=2
m/s,即W3<0,D正确.
3.
(2020·安徽安庆市模拟)如图8所示,固定的光滑竖直杆上套着一个滑块,滑块用轻绳系着绕过光滑的定滑轮O.现以大小不变的拉力F拉绳,使滑块从A点起由静止开始上升.滑块运动到C点时速度最大.已知滑块质量为m,滑轮O到竖直杆的距离为d,∠OAO′=37°,∠OCO′=53°,重力加速度为g.求:(sin
37°=0.6,cos
37°=0.8)
图8
(1)拉力F的大小;
(2)滑块由A到C过程中拉力F做的功.
【答案】(1)mg (2)mgd
【解析】(1)滑块运动到C点时速度最大,则在C点有
Fcos
53°=mg
解得F=mg.
(2)由能量守恒可知,拉力F对绳端点做的功就等于绳的拉力F对滑块做的功.
滑轮与A间绳长L1=
滑轮与C间绳长L2=
则滑轮右侧绳子增加的长度
ΔL=L1-L2=-=
故拉力做的功W=FΔL=mgd.
考点二
功率
机车启动
(一)典例剖析
例1某大瀑布的平均水流量为,水的落差为。已知水的密度为。在大瀑布水流下落过程中,重力做功的平均功率约为
(
)
A.
B.
C.
D.
【答案】D
【解析】每秒钟水流的质量为,重力做功的平均功率约为,选项D正确。
【易错点】没有真正理解平均功率的公式。
【方法点拨】理解瞬时功率和平均功率公式和区别是解题的关键。
例2(多选)(2019·江苏苏州市调研)质量为2×103
kg的汽车由静止开始沿平直公路行驶,行驶过程中牵引力F和车速倒数的关系图象如图8所示.已知行驶过程中最大车速为30
m/s,设阻力恒定,则( )
图8
A.汽车所受阻力为6×103
N
B.汽车在车速为5
m/s时,加速度为3
m/s2
C.汽车在车速为15
m/s时,加速度为1
m/s2
D.汽车在行驶过程中的最大功率为6×104
W
【答案】CD
【解析】当牵引力等于阻力时,速度最大,由题图可知阻力大小Ff=2
000
N,故A错误;车速为5
m/s时,汽车的加速度a=
m/s2=2
m/s2,故B错误;题中倾斜图线的斜率表示汽车的额定功率,可知P=Ffv=2
000×30
W=6×104
W,当车速为15
m/s时,牵引力F==
N=4
000
N,则加速度a′==
m/s2=1
m/s2,故C正确;汽车的最大功率等于额定功率,等于6×104
W,故D正确.
【易错点】不能正确运用图象。
【方法点拨】充分利用图象,找出图象中的有效信息。
例3汽车在平直公路上以速度v0匀速行驶,发动机功率为P.快进入闹区时,司机减小了油门,使汽车的功率立即减小一半并保持该功率继续行驶.下面四个图象中,哪个图象正确表示了从司机减小油门开始,汽车的速度与时间的关系( )
【答案】C
【解析】功率减小一半时,由于惯性汽车速度来不及变化,根据功率和速度关系公式P=Fv,此时牵引力减小一半,小于阻力,汽车做减速运动,由公式P=Fv可知,功率一定时,速度减小后,牵引力增大,合力减小,加速度减小,故汽车做加速度越来越小的减速运动,当牵引力增大到等于阻力时,汽车做匀速运动,C正确.
【易错点】误认为功率变化的瞬间速度会突变。
【方法点拨】当功率变化的瞬间牵引力会发生突变,从而引起加速度的变化,最终导致了速度的变化。
(二)举一反三
1.
把A、B两相同小球在离地面同一高度处以相同大小的初速度v0分别沿水平方向和竖直方向抛出,不计空气阻力,如图10所示,则下列说法正确的是( )
图10
A.两小球落地时速度相同
B.两小球落地时,重力的瞬时功率相同
C.从开始运动至落地,重力对两小球做的功相同
D.从开始运动至落地,重力对两小球做功的平均功率相同
【答案】C
【解析】A、B两球落地的速度大小相同,方向不同,A错误;由P=mg·v竖可知,因B球落地时竖直速度较大,故PB>PA,B错误;重力做功与路径无关,均为mgh,C正确;因B球从抛出到落地所用时间较长,故A>B,D错误。
2.
(多选)一质量为1
kg的质点静止于光滑水平面上,从t=0时刻开始,受到水平外力F作用,如图11所示.下列判断正确的是( )
图11
A.0~2
s内外力的平均功率是4
W
B.第2
s内外力所做的功是4
J
C.第2
s末外力的瞬时功率最大
D.第1
s末与第2
s末外力的瞬时功率之比为9∶4
【答案】AD
【解析】第1
s末质点的速度
v1=t1=×1
m/s=3
m/s.
第2
s末质点的速度
v2=v1+t2=(3+×1)
m/s=4
m/s.
则第2
s内外力做功W2=mv-mv=3.5
J
0~2
s内外力的平均功率
P==
W=4
W.
选项A正确,选项B错误;
第1
s末外力的瞬时功率P1=F1v1=3×3
W=9
W,
第2
s末外力的瞬时功率P2=F2v2=1×4
W=4
W,故
P1∶P2=9∶4.选项C错误,选项D正确.
3.
一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数的关系图像如图12所示。若已知汽车的质量,则根据图像所给的信息,不能求出的物理量是( )
图12
A.汽车的功率
B.汽车行驶的最大速度
C.汽车所受到的阻力
D.汽车运动到最大速度所需的时间
【答案】D
【解析】由F-Ff=ma,P=Fv可得:a=·-,对应图线可知,=k=40,可求出汽车的功率P,由a=0时,=0.05可得:vm=20
m/s,再由vm=,可求出汽车受到的阻力Ff,但无法求出汽车运动到最大速度所需的时间。
考点三
动能定理及其应用
(一)典例剖析
例1如图13所示,AB为圆弧轨道,BC为水平直轨道,BC恰好在B点与AB相切,圆弧的半径为R,BC的长度也是R.一质量为m的物体与两个轨道间的动摩擦因数都为μ,它由轨道顶端A从静止开始下落,恰好运动到C处停止,重力加速度为g,那么物体在AB段克服摩擦力所做的功为( )
图13
A.
B.
C.mgR
D.(1-μ)mgR
【答案】D
【解析】设物体在AB段克服摩擦力所做的功为WAB,物体从A到C的全过程,根据动能定理有mgR-WAB-μmgR=0,所以WAB=mgR-μmgR=(1-μ)mgR,故D正确.
【易错点】不能正确写出动能定理的表达式。
【方法点拨】对整个过程进行分析,列出动能定理表达式进行求解。
例2(多选)如图14所示,一块长木板B放在光滑的水平面上,在B上放一物体A,现以恒定的外力拉B,由于A、B间摩擦力的作用,A将在B上滑动,以地面为参考系,A、B都向前移动了一段距离.在此过程中( )
图14
A.外力F做的功等于A和B动能的增量
B.B对A的摩擦力所做的功等于A的动能的增量
C.A对B的摩擦力所做的功等于B对A的摩擦力所做的功
D.外力F对B做的功等于B的动能的增量与B克服摩擦力所做的功之和
【答案】BD
【解析】A物体所受的合外力等于B对A的摩擦力,对A物体运用动能定理,则有B对A的摩擦力所做的功等于A的动能的增量,B正确;A对B的摩擦力与B对A的摩擦力是一对作用力与反作用力,大小相等,方向相反,但是由于A在B上滑动,A、B相对地面的位移不相等,故二者做功不相等,C错误;对B应用动能定理WF-Wf=ΔEkB,则WF=ΔEkB+Wf,即外力F对B做的功等于B的动能的增量与B克服摩擦力所做的功之和,D正确;根据功能关系可知,外力F做的功等于A和B动能的增量与产生的内能之和,故A错误.
【易错点】不能区分各摩擦力的做功的问题。
【方法点拨】区分各摩擦力做功。
例3如图15所示,用一块长L1=1.0
m的木板在墙和桌面间架设斜面,桌子高H=0.8
m,长L2=1.5
m.斜面与水平桌面的夹角θ可在0~60°间调节后固定.将质量m=0.2
kg的小物块从斜面顶端静止释放,物块与斜面间的动摩擦因数μ1=0.05,物块与桌面间的动摩擦因数为μ2,忽略物块在斜面与桌面交接处的能量损失.(重力加速度取g=10
m/s2;最大静摩擦力等于滑动摩擦力)
图15
(1)求θ角增大到多少时,物块能从斜面开始下滑;(用正切值表示)
(2)当θ角增大到37°时,物块恰能停在桌面边缘,求物块与桌面间的动摩擦因数μ2;(已知sin
37°=0.6,cos
37°=0.8)
(3)继续增大θ角,发现θ=53°时物块落地点与墙面的距离最大,求此最大距离xm.
【答案】(1)arctan
0.05 (2)0.8 (3)1.9
m
【解析】(1)为使小物块下滑,应有mgsin
θ≥μ1mgcos
θ①
θ满足的条件tan
θ≥0.05②
即当θ=arctan
0.05时物块恰好从斜面开始下滑.
(2)克服摩擦力做功Wf=μ1mgL1cos
θ+μ2mg(L2-L1cos
θ)③
由动能定理得mgL1sin
θ-Wf=0④
代入数据得μ2=0.8⑤
(3)由动能定理得mgL1sin
θ-Wf=mv2⑥
结合③式并代入数据得v=1
m/s⑦
由平抛运动规律得H=gt2,x1=vt
解得t=0.4
s⑧
x1=0.4
m⑨
xm=x1+L2=1.9
m
【易错点】不能准确的分析出物体的整个运动过程
【方法点拨】进行物理模型的分解,对每个模型进行单独分析,并找出模型间的相关联的物理量。
(二)举一反三
1.
(多选)质量不等,但有相同动能的两个物体,在动摩擦因数相同的水平地面上滑行,直至停止,则( ).
A.质量大的物体滑行的距离大
B.质量小的物体滑行的距离大
C.它们滑行的距离一样大
D.它们克服摩擦力所做的功一样多
【答案】BD
【解析】由动能定理可得-Ffx=0-Ek,即μmgx=Ek,由于动能相同动摩擦因数相同,故质量小的滑行距离大,它们克服摩擦力所做的功都等于Ek.
2.
(2018·全国卷Ⅱ)如图16,某同学用绳子拉动木箱,使它从静止开始沿粗糙水平路面运动至具有某一速度.木箱获得的动能一定( )
图16
A.小于拉力所做的功
B.等于拉力所做的功
C.等于克服摩擦力所做的功
D.大于克服摩擦力所做的功
【答案】A
【解析】由题意知,W拉-W克摩=ΔEk,则W拉>ΔEk,A项正确,B项错误;W克摩与ΔEk的大小关系不确定,C、D项错误.
3.
如图17甲所示,轻弹簧左端固定在竖直墙上,右端点在O位置.质量为m的物块A(可视为质点)以初速度v0从距O点右方x0的P点处向左运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回.A离开弹簧后,恰好回到P点.物块A与水平面间的动摩擦因数为μ.求:
图17
(1)物块A从P点出发又回到P点的过程,克服摩擦力所做的功.
(2)O点和O′点间的距离x1.
(3)如图乙所示,若将另一个与A完全相同的物块B(可视为质点)与弹簧右端拴接,将A放在B右边,向左推A、B,使弹簧右端压缩到O′点位置,然后从静止释放,A、B共同滑行一段距离后分离.分离后物块A向右滑行的最大距离x2是多少?
【答案】(1)mv (2)-x0 (3)x0-
【解析】(1)物块A从P点出发又回到P点的过程,根据动能定理得克服摩擦力所做的功为Wf=mv.
(2)物块A从P点出发又回到P点的过程,根据动能定理得2μmg(x1+x0)=mv
解得x1=-x0
(3)A、B在弹簧处于原长处分离,设此时它们的共同速度是v1,弹出过程弹力做功WF
只有A时,从O′到P有WF-μmg(x1+x0)=0-0
A、B共同从O′到O有WF-2μmgx1=×2mv
分离后对A有mv=μmgx2
联立以上各式可得x2=x0-.
四、分层训练
能力进阶
【基础】
1.
(多选)
(2019·宁夏银川市质检)如图18所示为一滑草场.某条滑道由上下两段高均为h,与水平面倾角分别为45°和37°的滑道组成,载人滑草车与草地之间的动摩擦因数为μ.质量为m的载人滑草车从坡顶由静止开始自由下滑,经过上、下两段滑道后,最后恰好静止于滑道的底端(不计载人滑草车在两段滑道交接处的能量损失,重力加速度为g,sin
37°=0.6,cos
37°=0.8).则( )
图18
A.动摩擦因数μ=
B.载人滑草车最大速度为
C.载人滑草车克服摩擦力做功为mgh
D.载人滑草车在下段滑道上的加速度大小为g
【答案】AB
【解析】对载人滑草车从坡顶由静止开始滑到底端的全过程分析,由动能定理可知:mg·2h-μmgcos
45°·-μmgcos
37°·=0,解得μ=,选项A正确;
对经过上段滑道的过程分析,根据动能定理有mgh-μmgcos
45°·=mv,解得:vm=,选项B正确;载人滑草车克服摩擦力做功为2mgh,选项C错误;载人滑草车在下段滑道上的加速度为a==-g,故大小为g,选项D错误.
2.如图19所示,质量为m的小球以初速度v0水平抛出,恰好垂直打在倾角为θ的斜面上,则小球落在斜面上时重力的瞬时功率为(不计空气阻力)( )
图19
A.mgv0tan
θ
B.
C.
D.mgv0cos
θ
【答案】B
【解析】小球落在斜面上时重力的瞬时功率为P=mgvy,而vytan
θ=v0,所以P=,B正确。
2.
(2019·安徽合肥市第二次质检)如图20甲所示,置于水平地面上质量为m的物体,在竖直拉力F作用下,由静止开始向上运动,其动能Ek与距地面高度h的关系图象如图乙所示,已知重力加速度为g,空气阻力不计.下列说法正确的是( )
图20
A.在0~h0过程中,F大小始终为mg
B.在0~h0和h0~2h0过程中,F做功之比为2∶1
C.在0~2h0过程中,物体的机械能不断增加
D.在2h0~3.5h0过程中,物体的机械能不断减少
【答案】C
【解析】0~h0过程中,Ek-h图象为一段直线,由动能定理得:(F-mg)h0=mgh0-0,故F=2mg,A错误;由A可知,在0~h0过程中,F做功为2mgh0,在h0~2h0过程中,由动能定理可知,WF-mgh0=1.5mgh0-mgh0,解得WF=1.5mgh0,因此在0~h0和h0~2h0过程中,F做功之比为4∶3,故B错误;在0~2h0过程中,F一直做正功,故物体的机械能不断增加,C正确;在2h0~3.5h0过程中,由动能定理得WF′-1.5mgh0=0-1.5mgh0,则WF′=0,故F做功为0,物体的机械能保持不变,故D错误.
3.
如图21所示,演员正在进行杂技表演。由图可估算出他将一只鸡蛋抛出的过程中对鸡蛋所做的功最接近于(
)
图21
A.0.3J
B.3J
C.30J
D.300J
【答案】A
【解析】生活经验告诉我们:10个鸡蛋大约1斤即0.5kg,则一个鸡蛋的质量约为,鸡蛋大约能抛高度h=0.6m,则做功约为W=mgh=0.05×10×0.6J=0.3J,A正确。
4.
在离地面高为h处竖直上抛一质量为m的物块,抛出时的速度为v0,它落到地面时的速度为v,用g表示重力加速度,则在此过程中物块克服空气阻力所做的功等于( )
A.mgh-mv2-mv
B.-mv2-mv-mgh
C.mgh+mv-mv2
D.mgh+mv2-mv
【答案】C
【解析】对物块从h高处竖直上抛到落地的过程,根据动能定理可得mgh-Wf=mv2-mv,解得Wf=mgh+mv-mv2,选项C正确.
5.
一个25
kg的小孩从高度为3.0
m的滑梯顶端由静止开始滑下,滑到底端时的速度为2.0
m/s.取g=10
m/s2,关于力对小孩做的功,以下结果正确的是( ).
A.合外力做功50
J
B.阻力做功500
J
C.重力做功500
J
D.支持力做功50
J
【答案】A
【解析】合外力做的功W合=Ek-0,即W合=mv2=×25×22
J=50
J,A项正确;WG+W阻=Ek-0,故W阻=mv2-mgh=50
J-750
J=-700
J,B项错误;重力做功WG=mgh=25×10×3
J=750
J,C错;小孩所受支持力方向上的位移为零,故支持力做的功为零,D错.
【巩固】
1.
(多选)
(2020·山西运城市质检)质量为m的物体放在水平面上,它与水平面间的动摩擦因数为μ,重力加速度为g.用水平力拉物体,运动一段时间后撤去此力,最终物体停止运动.物体运动的v-t图象如图22所示.下列说法正确的是( )
图22
A.水平拉力大小为F=m
B.物体在0~3t0时间内的位移大小为v0t0
C.在0~3t0时间内水平拉力做的功为mv
D.在0~3t0时间内物体克服摩擦力做功的平均功率为μmgv0
【答案】BD
【解析】根据v-t图象和牛顿第二定律可知F-μmg=m,故选项A错误;由v-t图象与t坐标轴所围面积表示位移可知,在0~3t0时间内的位移大小为x=·3t0·v0=v0t0,所以选项B正确;在0~3t0时间内由动能定理可知W-μmgx=0,故水平拉力做的功W=μmgv0t0,又Ff=μmg=,则W=mv,选项C错误;在0~3t0时间内物体克服摩擦力做功的平均功率为===μmgv0,所以选项D正确.
2.一个质量为m的小球做自由落体运动,那么,在前t秒内重力对它做功的平均功率及在t秒末重力做功的瞬时功率P分别为( )
A.=mg2t2,P=mg2t2
B.=mg2t2,P=mg2t2
C.=mg2t,P=mg2t
D.=mg2t,P=2mg2t
【答案】C
【解析】前t秒内重力做功的平均功率===mg2t;t秒末重力做功的瞬时功率P=Fv=mg·gt=mg2t,故C正确.
3.
如图23是质量为1
kg的质点在水平面上运动的v-t图象,以水平向右的方向为正方向.以下判断正确的是( )
图23
A.在0~3.0
s时间内,合力对质点做功为10
J
B.在4.0~6.0
s时间内,质点的平均速度为3
m/s
C.在1.0~5.0
s时间内,合力的平均功率为4
W
D.在t=6.0
s时,质点的加速度为零
【答案】B
【解析】在0~3.0
s时间内,由动能定理W合=ΔEk=6
J,所以A错误.在4.0~6.0
s时间内,由图象可知s=6
m,==3
m/s,所以B正确.在1.0~5.0
s时间内,W合=ΔEk=8
J,==2
W,C错误.由题图可知,t=6.0
s时质点的加速度a=-4
m/s2,D错误.
4.
某汽车以额定功率在水平路面上行驶,空载时的最大速度为v1,装满货物后的最大速度为v2,已知汽车空车的质量为m0,汽车所受的阻力跟车重成正比,则汽车后来所装货物的质量是( )
A.m0
B.m0
C.m0
D.m0
【答案】A
【解析】当汽车空载时,有:P=Ff1v1=km0gv1,当汽车装满货物后,有:P=Ff2v2=k(m0+m)gv2
联立两式解得:m=m0.故A正确,B、C、D错误.
5.
用铁锤把小铁钉钉入木板,设木板对钉子的阻力与钉进木板的深度成正比,已知铁锤第一次将钉子钉进d,如果铁锤第二次敲钉子时对钉子做的功与第一次相同,那么,第二次钉子进入木板的深度是( )
A.(-1)
d
B.(-1)d
C.d
D.d
【答案】B
【解析】在将钉子钉入木板的过程中,随着深度的增加,阻力成正比地增加,这属于变力做功问题,由于力与位移成正比,可求出力对位移的平均值,将变力转化为恒力来处理.
根据题意可得
第一次做功:W=F1d=d.
第二次做功:W=F2d′=d′.
联立解得d′=(-1)d.
【拔高】
1.
(多选)
我国科学家正在研制航母舰载机使用的电磁弹射器.舰载机总质量为3.0×104
kg,设起飞过程中发动机的推力恒为1.0×105
N;弹射器有效作用长度为100
m,推力恒定.要求舰载机在水平弹射结束时速度大小达到80
m/s.弹射过程中舰载机所受总推力为弹射器和发动机推力之和,假设所受阻力为总推力的20%,则( )
A.弹射器的推力大小为1.1×106
N
B.弹射器对舰载机所做的功为1.1×108
J
C.弹射器对舰载机做功的平均功率为8.8×107
W
D.舰载机在弹射过程中的加速度大小为32
m/s2
【答案】ABD
【解析】设总推力为F,位移x=100
m,阻力F阻=20%F,对舰载机加速过程由动能定理得Fx-20%F·x=mv2,解得F=1.2×106
N,弹射器推力F弹=F-F发=1.2×106
N-1.0×105
N=1.1×106
N,A正确;弹射器对舰载机所做的功为W=F弹·x=1.1×106×100
J=1.1×108
J,B正确;弹射器对舰载机做功的平均功率=F弹·=4.4×107
W,C错误;根据运动学公式v2=2ax,得a==32
m/s2,D正确.
2.
在地面上某处将一金属小球竖直向上拋出,上升一定高度后再落回原处,若不考虑空气阻力,则下列图象能正确反映小球的速度、加速度、位移和动能随时间变化关系的是(取向上为正方向)( )
【答案】A
【解析】小球运动过程中加速度不变,B错;速度均匀变化先减小后反向增大,A对;位移和动能与时间不是线性关系,C、D错.
3.(2020年全国II卷)如图24所示,在摩托车越野赛途中的水平路段前方有一个坑,该坑沿摩托车前进方向的水平宽度为3h,其左边缘a点比右边缘b点高0.5h.若摩托车经过a点时的动能为E1,它会落到坑内c点.c与a的水平距离和高度差均为h;若经过a点时的动能为E2,该摩托车恰能越过坑到达b点.等于(
)
A.20
B.18
C.9.0
D.3.0
【答案】B
【解析】由题意可知两次平抛运动的竖直位移之比为2:1,水平位移之比为1:3,根据,x=v0t可得,,由可得,所以B正确。
4.(2019·河南平顶山市一轮复习质检)如图25所示,半径为r的半圆弧轨道ABC固定在竖直平面内,直径AC水平,一个质量为m的物块从圆弧轨道A端正上方P点由静止释放,物块刚好从A点无碰撞地进入圆弧轨道并做匀速圆周运动,到B点时对轨道的压力大小等于物块重力的2倍,重力加速度为g,不计空气阻力,不计物块的大小,则:
图25
(1)物块到达A点时的速度大小和PA间的高度差分别为多少?
(2)物块从A运动到B所用时间和克服摩擦力做的功分别为多少?
【答案】(1) (2) mgr
【解析】(1)设物块在B点时的速度为v,由牛顿第二定律得:FN-mg=m,
因为FN=2mg,所以v=,
因为物块从A点进入圆弧轨道并做匀速圆周运动,所以物块到达A点时速度大小为;
设PA间的高度差为h,从P到A的过程由动能定理得:mgh=mv2,所以h=.
(2)因为物块从A点进入圆弧轨道并做匀速圆周运动,所以物块从A运动到B所用时间t==;
从A运动到B由动能定理有:mgr-W克f=0,解得:W克f=mgr.
5.
(2019·河南名校联盟高三下学期联考)如图26所示,AB是一段位于竖直平面内的光滑轨道,高度为h,末端B处的切线方向水平.一个质量为m的小物体P从轨道顶端A处由静止释放,滑到B端后飞出,落到地面上的C点,轨迹如图中虚线BC所示.已知它落地时相对于B点的水平位移OC
=
l.现在轨道下方紧贴B点安装一水平木板,木板的右端与B的距离为,让P再次从A点由静止释放,它离开轨道并在木板上滑行后从右端水平飞出,仍然落在地面的C点.求:(不计空气阻力,重力加速度为g)
图26
(1)P滑至B点时的速度大小;
(2)P与木板之间的动摩擦因数μ.
【答案】(1) (2)
【解析】(1)物体P在AB轨道上滑动时,根据动能定理mgh=mv
得物体P滑到B点时的速度大小为v0=
(2)当没有木板时,物体离开B点后做平抛运动,设运动时间为t,有:
t==
当在轨道下方紧贴B点安装木板时,物体从木板右端水平抛出,在空中运动的时间也为t,水平位移为,因此物体从木板右端抛出的速度v1==
根据动能定理,物体在木板上滑动时,有
-μmg=mv-mv
解得物体P与木板之间的动摩擦因数μ=.
同课章节目录
