人教版数学八年级上册:12.3 角的平分线的性质 同步练习(2课时 Word版 附答案)
文档属性
| 名称 | 人教版数学八年级上册:12.3 角的平分线的性质 同步练习(2课时 Word版 附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 158.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 19:07:25 | ||
图片预览




文档简介
12.3 角的平分线的性质
第1课时 角的平分线的性质
40322504114801.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA
C.AAS D.角的平分线上的点到角两边的距离相等
2.已知△ABC,用尺规作图作出∠ABC的平分线(保留作图痕迹,但不写作法).
3.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( )
A.PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD
第3题图 第4题图
4.如图,在△ABC中,∠A=90°,BD是角平分线,DE⊥BC,垂足是E,AC=10 cm,CD=6 cm,则DE的长为( )
A.10 cm B.6 cm C.4 cm D.2 cm
5.如图,已知点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D,E,求证:OB=OC.
6.命题“全等三角形对应边上的高线相等”的已知是 ,结论是 .
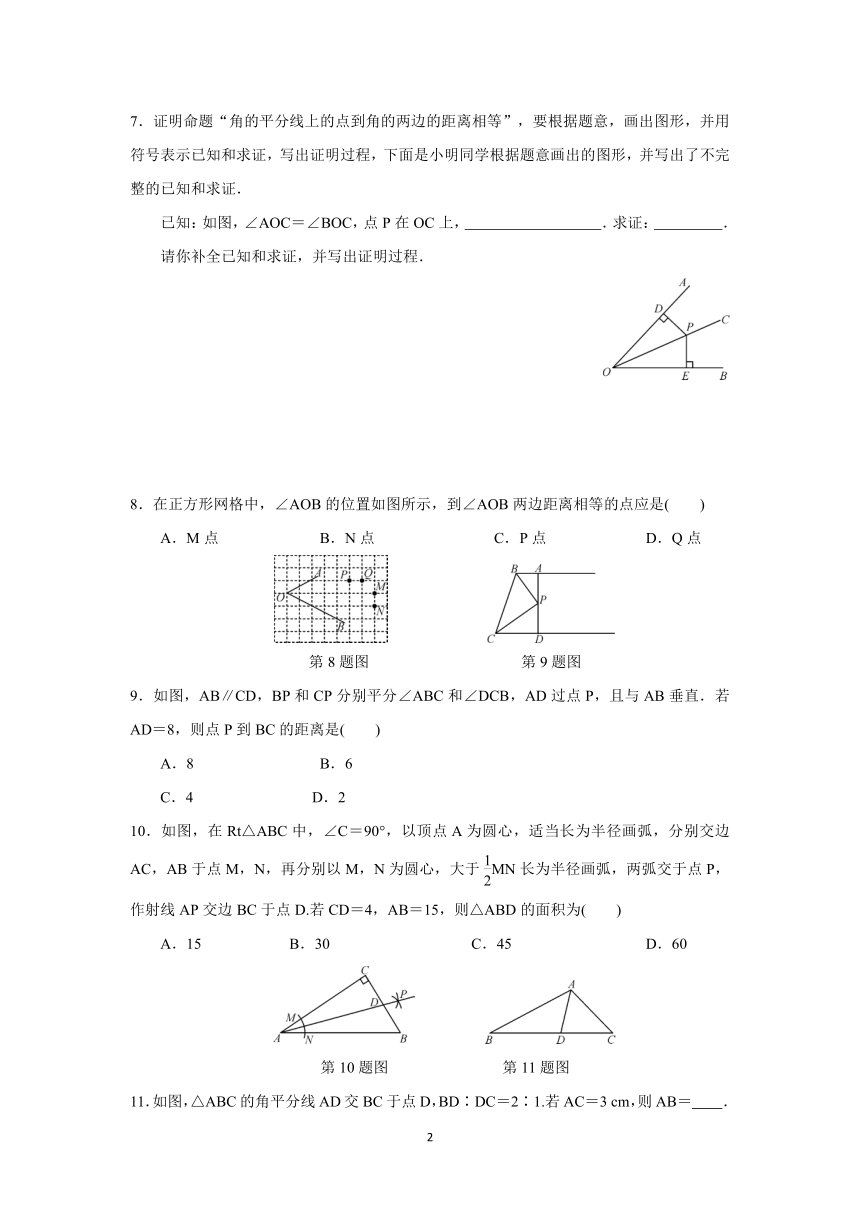
7.证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上, .求证: .
请你补全已知和求证,并写出证明过程.
8.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.M点 B.N点 C.P点 D.Q点
第8题图 第9题图
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8 B.6
C.4 D.2
10.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC,AB于点M,N,再分别以M,N为圆心,大于MN长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=4,AB=15,则△ABD的面积为( )
A.15 B.30 C.45 D.60
第10题图 第11题图
11.如图,△ABC的角平分线AD交BC于点D,BD∶DC=2∶1.若AC=3 cm,则AB= .
12.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,且AB=10 cm,求△DEB的周长.
13.证明:全等三角形对应边上的中线相等.
如图,已知△ABC≌△A′B′C′,AD,A′D′分别是BC,B′C′边上的中线.求证:AD=A′D′.
14.感知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易证:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证:DB=DC.
第2课时 角的平分线的判定
1.如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB.下列条件中:①∠AOC=∠BOC;②PD=PE;③OD=OE;④∠DPO=∠EPO.能判定OC是∠AOB的平分线的有( )
A.1个 B.2个 C.3个 D.4个
第1题图 第2题图
2.如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ= .
3.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,求证:AD是∠BAC的平分线.
4.到△ABC的三条边距离相等的点是△ABC的( )
A.三条中线的交点 B.三条角平分线的交点
C.三条高的交点 D.以上均不对
5.如图,△ABC的三边AB,BC,CA的长分别为40,50,60,其三条角平分线交于点O,则S△ABO∶S△BCO∶S△CAO= .
6.如图,铁路OA和铁路OB交于点O处,河道AB与铁路分别交于A处和B处,试在河岸上建一座水厂M,要求M到铁路OA,OB的距离相等,则该水厂M应建在图中什么位置?请在图中标出M点的位置.
7.D,E分别是△ABC中边AB,AC上的一点,在△ABC内有一点O,使OE=OD,则AO平分∠CAB吗?
解:AO平分∠CAB.理由如下:
∵点O到∠CAB两边的距离相等,
∴点O在∠CAB的平分线上.
∴AO平分∠CAB.
以上解法是否正确?若不正确,请说明理由,并写出正确的结论.
8.如图,AD⊥OB,BC⊥OA,垂足分别为D,C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小关系是( )
A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法确定
9.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30° B.35° C.45° D.60°
第9题图 第10题图
10.如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是 .
11.三条公路两两相交于A,B,C三点,现计划修建一个商品超市,要求这个超市到三条公路距离相等,则可供选择的地方有 处.
12.如图,∠ABC的平分线与∠ACB的外角平分线相交于点D,连接AD.求证:AD是∠BAC的外角平分线.
13.如图,在△ABC中,∠B=∠C,D是BC边上一动点,过点D作DE⊥AB,DF⊥AC,E,F分别为垂足,则当点D移动到什么位置时,AD恰好平分∠BAC?请说明理由.
411162532766014.如图,在四边形ABDC中,∠D=∠B=90°,O为BD的中点,且AO平分∠BAC.求证:
(1)CO平分∠ACD;
(2)OA⊥OC;
(3)AB+CD=AC.
参考答案:
12.3 角的平分线的性质
第1课时 角的平分线的性质
1.A
2.解:作图略.
3.B
4.C
5.证明:∵点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,
∴OE=OD,∠BEO=∠CDO=90°.
在△BEO与△CDO中,
∴△BEO≌△CDO(ASA).
∴OB=OC.
6.两个三角形是全等三角形,它们对应边上的高线相等.
7.证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
在△PDO和△PEO中,
∴△PDO≌△PEO(AAS).
∴PD=PE.
8.A
9.C
10.B
11.6cm.
12.解:∵AD平分∠BAC交BC于点D,DE⊥AB,∠C=90°,
∴CD=DE.
在Rt△ACD和Rt△AED中,
∴Rt△ACD≌Rt△AED(HL).
∴AE=AC.
∴△DEB的周长为DE+DB+EB=CD+DB+BE=BC+BE=AC+BE=AE+BE=AB=10 cm.
13.证明:∵△ABC≌△A′B′C′,
∴AB=A′B′,∠B=∠B′,BC=B′C′.
又∵AD,A′D′分别是BC,B′C′边上的中线,
∴BD=BC,B′D′=B′C′.
∴BD=B′D′.
在△ABD和△A′B′D′中,
∴△ABD≌△A′B′D′(SAS).
∴AD=A′D′.
14.证明:过点D分别作DE⊥AB于点E,DF⊥AC交AC的延长线于点F,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠DEB=∠F=90°.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD.
在△DFC和△DEB中,
∴△DFC≌△DEB(AAS).
∴DC=DB.
第2课时 角的平分线的判定
1.D
2. 35°.
3.证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠DFC=90°.
在Rt△DEB和Rt△DFC中,
∴Rt△DEB≌Rt△DFC(HL).∴DE=DF.
∴AD是∠BAC的平分线.
4.B
5.4∶5∶6.
6.解:图略.提示:作∠AOB的平分线,与AB的交点即为点M的位置.
7.解:不正确.以上解法忽视了OD,OE分别垂直于AB,AC的条件,故产生错误.正确的结论是“AO不一定平分∠CAB”.
8.A
9.B
10.31.5.
11.4.
12.
证明:过点D分别作DE⊥AB,DG⊥AC,DF⊥BC,垂足分别为E,G,F.
又∵BD平分∠ABC,CD平分∠ACF,
∴DE=DF,DG=DF.
∴DE=DG.
∴AD平分∠EAC,即AD是∠BAC的外角平分线.
13.解:移动到BC的中点时,AD恰好平分∠BAC.理由如下:
∵D是BC的中点,
∴BD=CD.
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°.
在△DEB和△DFC中,
∴△DEB≌△DFC(AAS).
∴DE=DF.
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC.
14.
证明:(1)过点O作OE⊥AC于点E.
∵∠B=90°,AO平分∠BAC,
∴OB=OE.
∵O为BD的中点,
∴OB=OD.
∴OE=OD.
又∵∠D=90°,∠OEC=90°,
∴CO平分∠ACD.
(2)在Rt△ABO和Rt△AEO中,
∴Rt△ABO≌△Rt△AEO(HL).
∴∠AOB=∠AOE=∠BOE.
同理,∠COD=∠COE=∠DOE.
∵∠AOC=∠AOE+∠COE,
∴∠AOC=∠BOE+∠DOE=×180°=90°.
∴OA⊥OC.
(3)∵Rt△ABO≌Rt△AEO,
∴AB=AE.同理可得CD=CE.
∵AC=AE+CE,∴AB+CD=AC.
第1课时 角的平分线的性质
40322504114801.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA
C.AAS D.角的平分线上的点到角两边的距离相等
2.已知△ABC,用尺规作图作出∠ABC的平分线(保留作图痕迹,但不写作法).
3.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( )
A.PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD
第3题图 第4题图
4.如图,在△ABC中,∠A=90°,BD是角平分线,DE⊥BC,垂足是E,AC=10 cm,CD=6 cm,则DE的长为( )
A.10 cm B.6 cm C.4 cm D.2 cm
5.如图,已知点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D,E,求证:OB=OC.
6.命题“全等三角形对应边上的高线相等”的已知是 ,结论是 .
7.证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上, .求证: .
请你补全已知和求证,并写出证明过程.
8.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.M点 B.N点 C.P点 D.Q点
第8题图 第9题图
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8 B.6
C.4 D.2
10.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC,AB于点M,N,再分别以M,N为圆心,大于MN长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=4,AB=15,则△ABD的面积为( )
A.15 B.30 C.45 D.60
第10题图 第11题图
11.如图,△ABC的角平分线AD交BC于点D,BD∶DC=2∶1.若AC=3 cm,则AB= .
12.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,且AB=10 cm,求△DEB的周长.
13.证明:全等三角形对应边上的中线相等.
如图,已知△ABC≌△A′B′C′,AD,A′D′分别是BC,B′C′边上的中线.求证:AD=A′D′.
14.感知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易证:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证:DB=DC.
第2课时 角的平分线的判定
1.如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB.下列条件中:①∠AOC=∠BOC;②PD=PE;③OD=OE;④∠DPO=∠EPO.能判定OC是∠AOB的平分线的有( )
A.1个 B.2个 C.3个 D.4个
第1题图 第2题图
2.如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ= .
3.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,求证:AD是∠BAC的平分线.
4.到△ABC的三条边距离相等的点是△ABC的( )
A.三条中线的交点 B.三条角平分线的交点
C.三条高的交点 D.以上均不对
5.如图,△ABC的三边AB,BC,CA的长分别为40,50,60,其三条角平分线交于点O,则S△ABO∶S△BCO∶S△CAO= .
6.如图,铁路OA和铁路OB交于点O处,河道AB与铁路分别交于A处和B处,试在河岸上建一座水厂M,要求M到铁路OA,OB的距离相等,则该水厂M应建在图中什么位置?请在图中标出M点的位置.
7.D,E分别是△ABC中边AB,AC上的一点,在△ABC内有一点O,使OE=OD,则AO平分∠CAB吗?
解:AO平分∠CAB.理由如下:
∵点O到∠CAB两边的距离相等,
∴点O在∠CAB的平分线上.
∴AO平分∠CAB.
以上解法是否正确?若不正确,请说明理由,并写出正确的结论.
8.如图,AD⊥OB,BC⊥OA,垂足分别为D,C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小关系是( )
A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.无法确定
9.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A.30° B.35° C.45° D.60°
第9题图 第10题图
10.如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是 .
11.三条公路两两相交于A,B,C三点,现计划修建一个商品超市,要求这个超市到三条公路距离相等,则可供选择的地方有 处.
12.如图,∠ABC的平分线与∠ACB的外角平分线相交于点D,连接AD.求证:AD是∠BAC的外角平分线.
13.如图,在△ABC中,∠B=∠C,D是BC边上一动点,过点D作DE⊥AB,DF⊥AC,E,F分别为垂足,则当点D移动到什么位置时,AD恰好平分∠BAC?请说明理由.
411162532766014.如图,在四边形ABDC中,∠D=∠B=90°,O为BD的中点,且AO平分∠BAC.求证:
(1)CO平分∠ACD;
(2)OA⊥OC;
(3)AB+CD=AC.
参考答案:
12.3 角的平分线的性质
第1课时 角的平分线的性质
1.A
2.解:作图略.
3.B
4.C
5.证明:∵点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,
∴OE=OD,∠BEO=∠CDO=90°.
在△BEO与△CDO中,
∴△BEO≌△CDO(ASA).
∴OB=OC.
6.两个三角形是全等三角形,它们对应边上的高线相等.
7.证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
在△PDO和△PEO中,
∴△PDO≌△PEO(AAS).
∴PD=PE.
8.A
9.C
10.B
11.6cm.
12.解:∵AD平分∠BAC交BC于点D,DE⊥AB,∠C=90°,
∴CD=DE.
在Rt△ACD和Rt△AED中,
∴Rt△ACD≌Rt△AED(HL).
∴AE=AC.
∴△DEB的周长为DE+DB+EB=CD+DB+BE=BC+BE=AC+BE=AE+BE=AB=10 cm.
13.证明:∵△ABC≌△A′B′C′,
∴AB=A′B′,∠B=∠B′,BC=B′C′.
又∵AD,A′D′分别是BC,B′C′边上的中线,
∴BD=BC,B′D′=B′C′.
∴BD=B′D′.
在△ABD和△A′B′D′中,
∴△ABD≌△A′B′D′(SAS).
∴AD=A′D′.
14.证明:过点D分别作DE⊥AB于点E,DF⊥AC交AC的延长线于点F,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠DEB=∠F=90°.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD.
在△DFC和△DEB中,
∴△DFC≌△DEB(AAS).
∴DC=DB.
第2课时 角的平分线的判定
1.D
2. 35°.
3.证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠DFC=90°.
在Rt△DEB和Rt△DFC中,
∴Rt△DEB≌Rt△DFC(HL).∴DE=DF.
∴AD是∠BAC的平分线.
4.B
5.4∶5∶6.
6.解:图略.提示:作∠AOB的平分线,与AB的交点即为点M的位置.
7.解:不正确.以上解法忽视了OD,OE分别垂直于AB,AC的条件,故产生错误.正确的结论是“AO不一定平分∠CAB”.
8.A
9.B
10.31.5.
11.4.
12.
证明:过点D分别作DE⊥AB,DG⊥AC,DF⊥BC,垂足分别为E,G,F.
又∵BD平分∠ABC,CD平分∠ACF,
∴DE=DF,DG=DF.
∴DE=DG.
∴AD平分∠EAC,即AD是∠BAC的外角平分线.
13.解:移动到BC的中点时,AD恰好平分∠BAC.理由如下:
∵D是BC的中点,
∴BD=CD.
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°.
在△DEB和△DFC中,
∴△DEB≌△DFC(AAS).
∴DE=DF.
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC.
14.
证明:(1)过点O作OE⊥AC于点E.
∵∠B=90°,AO平分∠BAC,
∴OB=OE.
∵O为BD的中点,
∴OB=OD.
∴OE=OD.
又∵∠D=90°,∠OEC=90°,
∴CO平分∠ACD.
(2)在Rt△ABO和Rt△AEO中,
∴Rt△ABO≌△Rt△AEO(HL).
∴∠AOB=∠AOE=∠BOE.
同理,∠COD=∠COE=∠DOE.
∵∠AOC=∠AOE+∠COE,
∴∠AOC=∠BOE+∠DOE=×180°=90°.
∴OA⊥OC.
(3)∵Rt△ABO≌Rt△AEO,
∴AB=AE.同理可得CD=CE.
∵AC=AE+CE,∴AB+CD=AC.
