人教版数学八年级上册:12.2 三角形全等的判定 练习题(Word版 附答案)
文档属性
| 名称 | 人教版数学八年级上册:12.2 三角形全等的判定 练习题(Word版 附答案) | 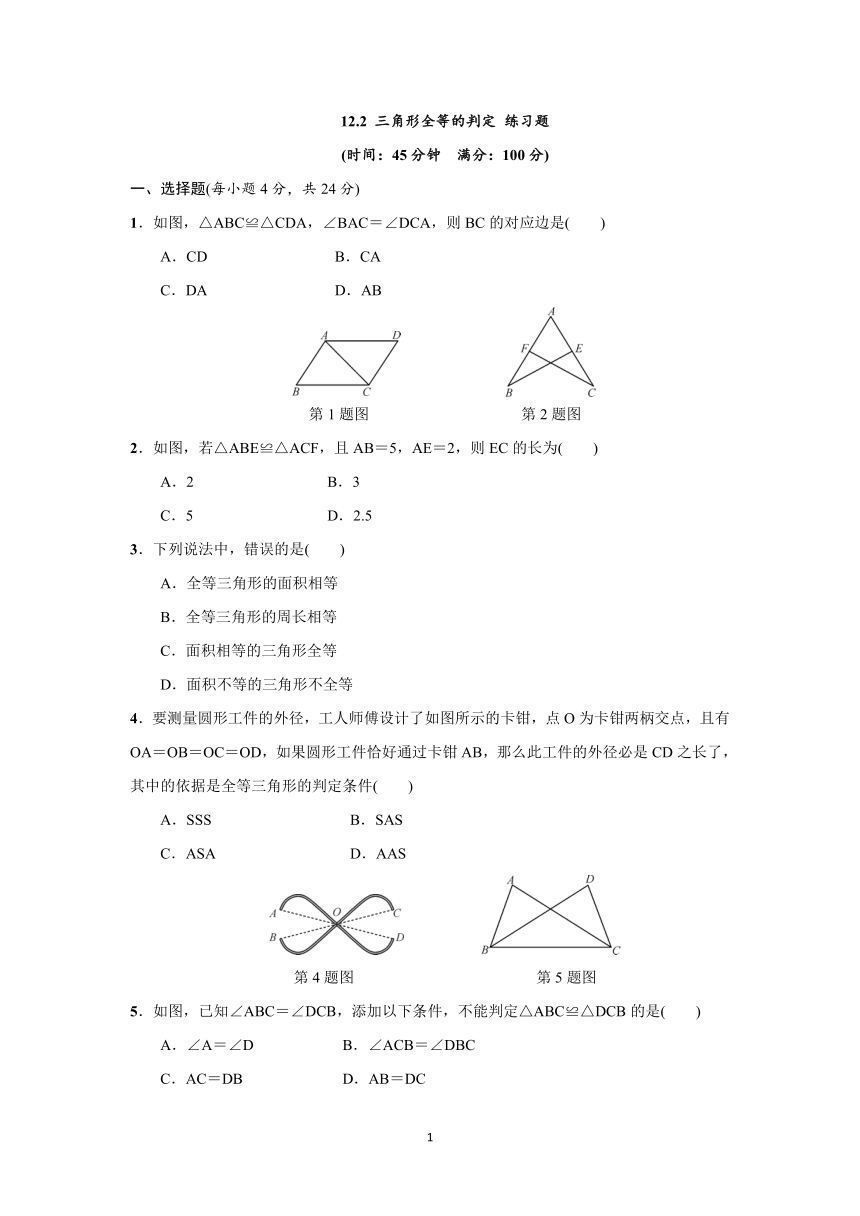 | |
| 格式 | docx | ||
| 文件大小 | 99.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 18:53:16 | ||
图片预览



文档简介
12.2 三角形全等的判定 练习题
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共24分)
1.如图,△ABC≌△CDA,∠BAC=∠DCA,则BC的对应边是( )
A.CD B.CA
C.DA D.AB
第1题图 第2题图
2.如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
A.2 B.3
C.5 D.2.5
3.下列说法中,错误的是( )
A.全等三角形的面积相等
B.全等三角形的周长相等
C.面积相等的三角形全等
D.面积不等的三角形不全等
4.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,那么此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
A.SSS B.SAS
C.ASA D.AAS
第4题图 第5题图
5.如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A.∠A=∠D B.∠ACB=∠DBC
C.AC=DB D.AB=DC
6.如图1,已知两个全等直角三角形的直角顶点及一条直角边重合.将△ACB绕点C按顺时针方向旋转到△A′CB′的位置,其中A′C交直线AD于点E,A′B′分别交直线AD,AC于点F,G,则在图2中,全等三角形共有( )
A.5对 B.4对 C.3对 D.2对
二、填空题(每小题4分,共16分)
7.如图,△ABC≌△DEF,点A与点D,点B与点E分别是对应顶点,∠B=32°,∠A=68°,AB=13 cm,则∠F= 度,DE= cm.
8.如图,已知点A,D,B,F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是 .(只需填一个即可)
第8题图 第9题图
9.如图,△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB,垂足为E,则∠ADE的度数是 .
10.如图,AC=BC,∠ACB=90°,AE平分∠BAC,BF⊥AE,交AC的延长线于点F,且垂足为E,则下列结论:①AD=BF; ②BF=AF; ③AC+CD=AB;④AB=BF;⑤AD=2BE.其中正确的结论有 .(填序号)
三、解答题(共60分)
11.(8分)如图,点B,E,C,F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AC=DF.
12.(8分)如图,AC=AE,∠1=∠2,AB=AD.求证:BC=DE.
13.(10分)如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.
(1)求证:△ADC≌△CEB;
(2)若AD=5 cm,DE=3 cm,求BE的长度.
14.(10分)如图,已知PB⊥AB,PC⊥AC,且PB=PC,D是AP上的一点,求证:BD=CD.
15.(12分)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A,D重合,连接BE,EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
16.(12分)如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,点D为AB的中点,点P在线段BC上以3 cm/s的速度由B点向C点运动.同时,点Q在线段CA上以相同的速度由C点向A点运动,一个点到达终点后另一个点也停止运动,当△BPD与△CQP全等时,求P点运动的时间.
参考答案:
一、选择题(每小题4分,共24分)
题号
1
2
3
4
5
6
答案
C
B
C
B
C
B
二、填空题(每小题4分,共16分)
7. 80 , 13 .
8. ∠A=∠F或AC∥EF或BC=DE(答案不唯一).
9. 60°.
10. ①③⑤.
三、解答题(共60分)
11.证明:∵BE=CF,
∴BE-EC=CF-EC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
∴AC=DF.
12.证明:∵∠1=∠2,
∴∠CAB=∠EAD.
在△BAC和△DAE中,
,
∴△BAC≌△DAE(SAS).
∴BC=DE.
13.解:(1)证明:∵AD⊥CE,BE⊥CE,∠ACB=90°,
∴∠ADC=∠ACB=∠CEB=90°.
∴∠BCE=∠CAD.
在△ADC与△CEB中,
∴△ADC≌△CEB(AAS).
(2)由(1)知,△ADC≌△CEB,
则AD=CE=5 cm,CD=BE.
∵CD=CE-DE,
∴BE=AD-DE=5-3=2(cm).
14.证明:∵PB⊥AB,PC⊥AC,
∴∠PBA=∠PCA=90°.
在Rt△PBA和Rt△PCA中,
∴Rt△PBA≌Rt△PCA(HL).
∴∠APB=∠APC.
在△PBD和△PCD中,
∴△PBD≌△PCD(SAS).
∴BD=CD.
15.解:BE=EC,BE⊥EC.证明过程如下:
∵AC=2AB,点D是AC的中点,
∴AB=AD=CD.
∵∠EAD=∠EDA=45°,
∴∠EAB=∠EDC=135°.
在△EAB和△EDC中,
∴△EAB≌△EDC(SAS).
∴∠AEB=∠DEC,EB=EC.
∴∠AEB+∠BED=∠DEC+∠BED.
∴∠BEC=∠AED=90°.
∴BE=EC,BE⊥EC.
16.解:∵点D为AB的中点,AB=10 cm,
∴BD=AD=5 cm.
设点P运动的时间是x s,则BP=CQ=3x cm,CP=(8-3x)cm,
若BD与CQ是对应边,则BD=CQ,
∴5=3x.
∴x=.
此时BP=3x=5 cm,CP=8-3x=3 cm,BP≠CP,故舍去;
若BD与CP是对应边,则BD=CP,
∴5=8-3x.∴x=1,符合题意.
综上所述,点P运动的时间是1 s.
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共24分)
1.如图,△ABC≌△CDA,∠BAC=∠DCA,则BC的对应边是( )
A.CD B.CA
C.DA D.AB
第1题图 第2题图
2.如图,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
A.2 B.3
C.5 D.2.5
3.下列说法中,错误的是( )
A.全等三角形的面积相等
B.全等三角形的周长相等
C.面积相等的三角形全等
D.面积不等的三角形不全等
4.要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,点O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,那么此工件的外径必是CD之长了,其中的依据是全等三角形的判定条件( )
A.SSS B.SAS
C.ASA D.AAS
第4题图 第5题图
5.如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A.∠A=∠D B.∠ACB=∠DBC
C.AC=DB D.AB=DC
6.如图1,已知两个全等直角三角形的直角顶点及一条直角边重合.将△ACB绕点C按顺时针方向旋转到△A′CB′的位置,其中A′C交直线AD于点E,A′B′分别交直线AD,AC于点F,G,则在图2中,全等三角形共有( )
A.5对 B.4对 C.3对 D.2对
二、填空题(每小题4分,共16分)
7.如图,△ABC≌△DEF,点A与点D,点B与点E分别是对应顶点,∠B=32°,∠A=68°,AB=13 cm,则∠F= 度,DE= cm.
8.如图,已知点A,D,B,F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是 .(只需填一个即可)
第8题图 第9题图
9.如图,△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,DE⊥AB,垂足为E,则∠ADE的度数是 .
10.如图,AC=BC,∠ACB=90°,AE平分∠BAC,BF⊥AE,交AC的延长线于点F,且垂足为E,则下列结论:①AD=BF; ②BF=AF; ③AC+CD=AB;④AB=BF;⑤AD=2BE.其中正确的结论有 .(填序号)
三、解答题(共60分)
11.(8分)如图,点B,E,C,F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AC=DF.
12.(8分)如图,AC=AE,∠1=∠2,AB=AD.求证:BC=DE.
13.(10分)如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.
(1)求证:△ADC≌△CEB;
(2)若AD=5 cm,DE=3 cm,求BE的长度.
14.(10分)如图,已知PB⊥AB,PC⊥AC,且PB=PC,D是AP上的一点,求证:BD=CD.
15.(12分)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A,D重合,连接BE,EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
16.(12分)如图,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,点D为AB的中点,点P在线段BC上以3 cm/s的速度由B点向C点运动.同时,点Q在线段CA上以相同的速度由C点向A点运动,一个点到达终点后另一个点也停止运动,当△BPD与△CQP全等时,求P点运动的时间.
参考答案:
一、选择题(每小题4分,共24分)
题号
1
2
3
4
5
6
答案
C
B
C
B
C
B
二、填空题(每小题4分,共16分)
7. 80 , 13 .
8. ∠A=∠F或AC∥EF或BC=DE(答案不唯一).
9. 60°.
10. ①③⑤.
三、解答题(共60分)
11.证明:∵BE=CF,
∴BE-EC=CF-EC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
∴AC=DF.
12.证明:∵∠1=∠2,
∴∠CAB=∠EAD.
在△BAC和△DAE中,
,
∴△BAC≌△DAE(SAS).
∴BC=DE.
13.解:(1)证明:∵AD⊥CE,BE⊥CE,∠ACB=90°,
∴∠ADC=∠ACB=∠CEB=90°.
∴∠BCE=∠CAD.
在△ADC与△CEB中,
∴△ADC≌△CEB(AAS).
(2)由(1)知,△ADC≌△CEB,
则AD=CE=5 cm,CD=BE.
∵CD=CE-DE,
∴BE=AD-DE=5-3=2(cm).
14.证明:∵PB⊥AB,PC⊥AC,
∴∠PBA=∠PCA=90°.
在Rt△PBA和Rt△PCA中,
∴Rt△PBA≌Rt△PCA(HL).
∴∠APB=∠APC.
在△PBD和△PCD中,
∴△PBD≌△PCD(SAS).
∴BD=CD.
15.解:BE=EC,BE⊥EC.证明过程如下:
∵AC=2AB,点D是AC的中点,
∴AB=AD=CD.
∵∠EAD=∠EDA=45°,
∴∠EAB=∠EDC=135°.
在△EAB和△EDC中,
∴△EAB≌△EDC(SAS).
∴∠AEB=∠DEC,EB=EC.
∴∠AEB+∠BED=∠DEC+∠BED.
∴∠BEC=∠AED=90°.
∴BE=EC,BE⊥EC.
16.解:∵点D为AB的中点,AB=10 cm,
∴BD=AD=5 cm.
设点P运动的时间是x s,则BP=CQ=3x cm,CP=(8-3x)cm,
若BD与CQ是对应边,则BD=CQ,
∴5=3x.
∴x=.
此时BP=3x=5 cm,CP=8-3x=3 cm,BP≠CP,故舍去;
若BD与CP是对应边,则BD=CP,
∴5=8-3x.∴x=1,符合题意.
综上所述,点P运动的时间是1 s.
