北师大版九年级数学上册《第3章 概率的进一步认识》 单元练习卷(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学上册《第3章 概率的进一步认识》 单元练习卷(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 187.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 00:00:00 | ||
图片预览



文档简介
第3章 概率的进一步认识
一.选择题
1.连续掷两枚质地均匀的硬币,则两枚硬币都正面朝上的概率为( )
A. B. C. D.
2.甲盒子中装有3个乒乓球,分别标号为1,2,3;乙盒子中装有2个乒乓球,分别标号为1,2.现从每个盒子中随机取出1个球,则取出的两球标号之和为4的概率是( )
A. B. C. D.
3.在一个不适明的发子中装有四个小球,它们除分别标有的号码5,6,7,8不同外,其他完全相同若任意从袋子中摸出一球后不放同,再任意从袋子中摸出一球,则第二次摸出球的号码与第一次换出球的号码的和等于15的概率是( )
A. B. C. D.
4.某区响应国家提出的垃圾分类的号召,将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其他垃圾四类,并分别设置了相应的垃圾箱.为了解居民生活垃圾分类的情况,随机对该区四类垃圾箱中总计1000吨生活垃圾进行分拣后,统计数据如表:
垃圾箱种类 垃圾量
垃圾种类(吨) “厨余垃圾”箱 “可回收物”箱 “有害垃圾”箱 “其他垃圾”箱
厨余垃圾 400 100 40 60
可回收物 30 140 10 20
有害垃圾 5 20 60 15
其他垃圾 25 15 20 40
下列三种说法:
(1)厨余垃圾投放错误的有400t;
(2)估计可回收物投放正确的概率约为;
(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普.
其中正确的个数是( )
A.0 B.1 C.2 D.3
5.在不透明的袋子里装有16个红球和若干个白球,这些球除颜色不同外无其它差别.每次从袋子里摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.6,则袋中白球有( )
A.12个 B.20个 C.24个 D.40个
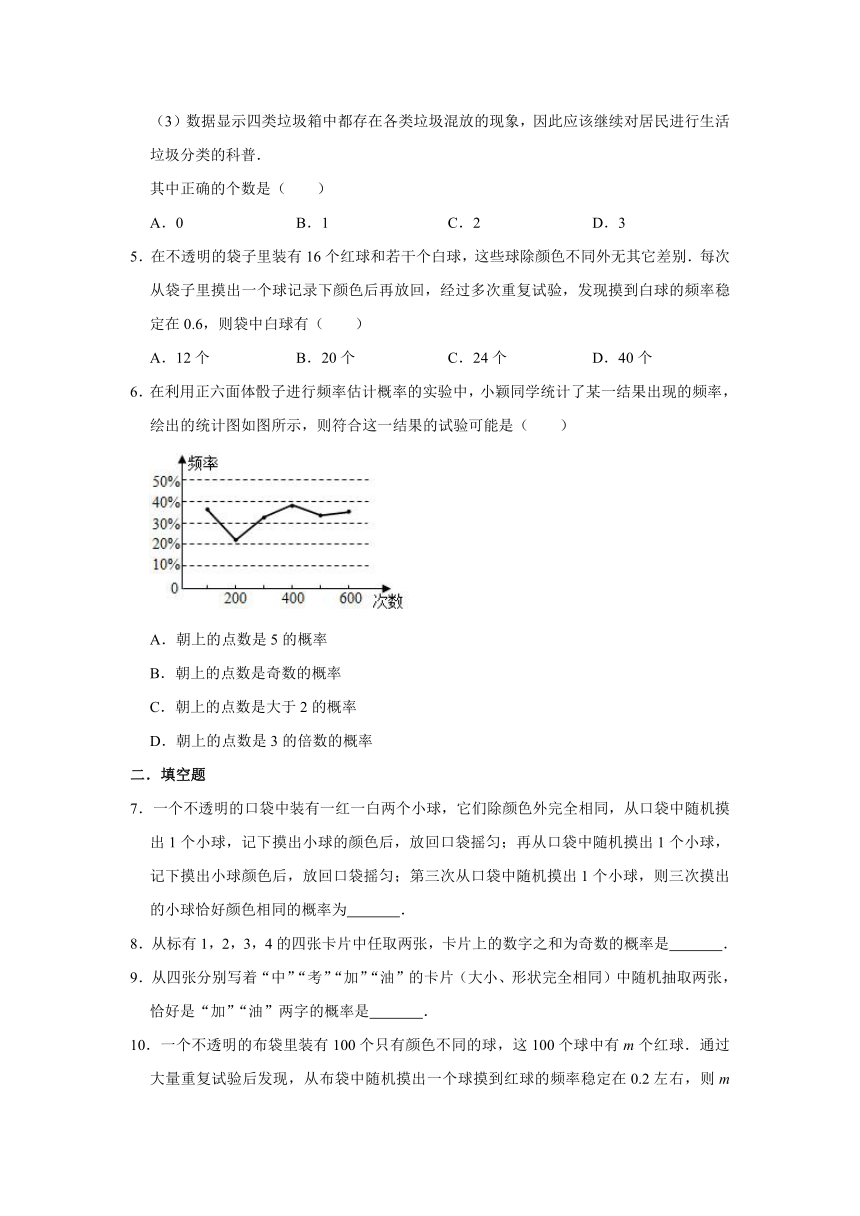
6.在利用正六面体骰子进行频率估计概率的实验中,小颖同学统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( )
A.朝上的点数是5的概率
B.朝上的点数是奇数的概率
C.朝上的点数是大于2的概率
D.朝上的点数是3的倍数的概率
二.填空题
7.一个不透明的口袋中装有一红一白两个小球,它们除颜色外完全相同,从口袋中随机摸出1个小球,记下摸出小球的颜色后,放回口袋摇匀;再从口袋中随机摸出1个小球,记下摸出小球颜色后,放回口袋摇匀;第三次从口袋中随机摸出1个小球,则三次摸出的小球恰好颜色相同的概率为 .
8.从标有1,2,3,4的四张卡片中任取两张,卡片上的数字之和为奇数的概率是 .
9.从四张分别写着“中”“考”“加”“油”的卡片(大小、形状完全相同)中随机抽取两张,恰好是“加”“油”两字的概率是 .
10.一个不透明的布袋里装有100个只有颜色不同的球,这100个球中有m个红球.通过大量重复试验后发现,从布袋中随机摸出一个球摸到红球的频率稳定在0.2左右,则m的值约为 .
11.在一个不透明的口袋中装有5个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,则估计口袋中白球大约有 个.
三.解答题
12.某中学开展黄梅戏演唱比赛,组委会将本次比赛的成绩(单位:分)进行整理,并绘制成如下频数分布表和频数分布直方图(不完整).
成绩 频数 频率
50≤x<60 2 0.04
60≤x<70 a 0.16
70≤x<80 20 0.40
80≤x<90 16 0.32
90≤x≤100 4 b
合计 50 1
请你根据图表提供的信息,解答下列问题:
(1)求出a,b的值并补全频数分布直方图.
(2)将此次比赛成绩分为三组:A.50≤x<60;B.60≤x<80;C.80≤x≤100若按照这样的分组方式绘制扇形统计图,则其中C组所在扇形的圆心角的度数是多少?
(3)学校准备从不低于90分的参赛选手中任选2人参加市级黄梅戏演唱比赛,求都取得了95分的小欣和小怡同时被选上的概率.
13.在一个不透明的布袋中,有三个除颜色外其它均相同的小球,其中两个黑色,一个红色?
(1)请用表格或树状图求出:一次随机取出2个小球,颜色不同的概率.
(2)如果老师在布袋中加入若干个红色小球.然后小明通过做实验的方式猜测加入的小球数,小明每次摸出一个小球记录下慎色并放回,实验数据如下表:
实验次数 100 200 300 400 500 1000
摸出红球 78 147 228 304 373 752
请你帮小明算出老师放入了多少个红色小球.
14.小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问:小明正好穿的是相同的一双袜子的概率是多少?
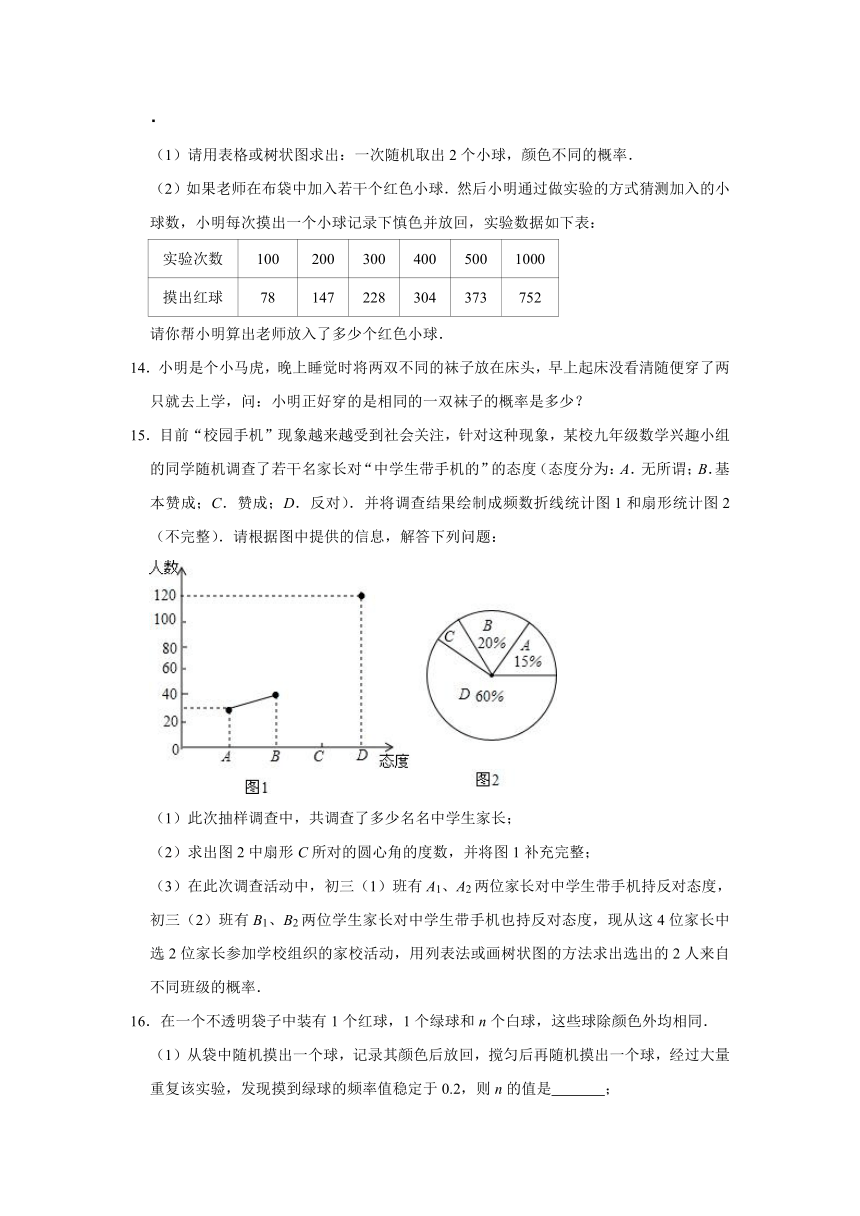
15.目前“校园手机”现象越来越受到社会关注,针对这种现象,某校九年级数学兴趣小组的同学随机调查了若干名家长对“中学生带手机的”的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对).并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)在此次调查活动中,初三(1)班有A1、A2两位家长对中学生带手机持反对态度,初三(2)班有B1、B2两位学生家长对中学生带手机也持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求出选出的2人来自不同班级的概率.
16.在一个不透明袋子中装有1个红球,1个绿球和n个白球,这些球除颜色外均相同.
(1)从袋中随机摸出一个球,记录其颜色后放回,搅匀后再随机摸出一个球,经过大量重复该实验,发现摸到绿球的频率值稳定于0.2,则n的值是 ;
(2)当n=2时,从该不透明的袋子中一次摸出两个球,求摸出的两个球颜色不同的概率.(用“画树状图”或“列表”的方法写出分析过程)
17.在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只.某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
(1)请估计:当n很大时,摸到白球的频率将会接近 ;
(2)试估计口袋中黑、白两种颜色的球各有多少只?
(3)请画树状图或列表计算:从中先摸出一个球,不放回,再摸出一个球,这两只球颜色不同的概率是多少?
18.为了准备体育艺术节的比赛,某篮球运动员在进行定点罚球训练,如表是部分训练记录:
罚球次数 20 40 60 80 100 120
命中次数 15 32 48 65 80 96
命中频率 0.75 0.8 0.8 0.81 0.8 0.8
(1)根据上表:估计该运动员罚球命中的概率是 ;
(2)根据上表分析,如果该运动员在一次比赛中共获得10次罚球机会(每次罚球投掷2次,每命中一次得1分),估计他罚球能得多少分,请说明理由.
参考答案
一.选择题
1. A.
2. B.
3. D.
4. C.
5. C.
6. D.
二.填空题
7. .
8. .
9. .
10. 20.
11. 15.
三.解答题
12.解:(1)a=50×0.16=8,b==0.08,补图如下:
(2)A、50≤x<60的人数所占的百分比是:×100%=4%,
B、60≤x<80的人数所占的百分比是:×100%=56%,
C、80≤x<100的人数所占的百分比是:×100%=40%,画图如下:
C组所在扇形的圆心角的度数为360°×(0.32+0.08)=144°;
(3)由题意知,不低于9(0分)的学生共有4人,设这四名学生分别为M,X,A,B,其中小欣和小怡分别用A,B表示,根据题意,画树状图如下.
由树状图可知,共有12种等可能的结果,其中小欣和小怡同时被选上的结果有2种,
故小欣和小怡同时被选上的概率是.
13.解:(1)根据题意列表如下:
黑1 黑2 红
黑1 / (黑1,黑2) (黑1,红)
黑2 (黑2,黑1) / (黑2,红)
红 (红,黑1) (红,黑2) /
列表如图,一共有6种等可能事件,其中颜色不同的等可能事件有4种,
∴颜色不同的概率为P==;
(2)由图表可得摸到红球概率为,
设加入了x个红球,则=,
解得x=5,
经检验x=5是原方程的解,
答:加入了5个红球.
14.解:设两双袜子分别为黑色和白色,
画树状图得:
∵共有12种等可能的结果,两只恰好配成同色的一双有4种情况,
∴小明正好穿的是相同的一双袜子的概率=,
15.解:(1)120÷60%=200(人),
所以调查的家长数为200人;
(2)扇形C所对的圆心角的度数=360°×(1﹣20%﹣15%﹣60%)=18°,
C类的家长数=200×(1﹣20%﹣15%﹣60%)=10(人),
补充图为:
(3)设初三(1)班两名家长为A1、A2,初三(2)班两名家长为B1,B2,
画树状图为
共有12种等可能结果,其中2人来自不同班级共有8种,
所以2人来自不同班级的概率==.
16.解:(1)根据题意得:=0.2,
解得:n=3,
则n的值为3,
故答案为:3;
(2)根据题意画图如下:
共有12种等情况数,其中摸出的两个球颜色不同的有10种,
则摸出的两个球颜色不同的概率是=.
17.解:(1)根据图表给出的数据可得,当n很大时,摸到白球的频率将会接近0.6;
答案为:0.6;
(2)由(1)摸到白球的概率为0.6,所以可估计口袋中白种颜色的球的个数是:5×0.6=3(只),
黑颜色的球有5﹣3=2(只);
(3)画树状图为:
共有20种等可能的结果数,其中两只球颜色不同占12种,
所以两只球颜色不同的概率==.
18.解:(1)根据表格数据可知该运动员罚球命中的概率0.8,
故答案为0.8;
(2)由题意可知,罚球一次命中概率为0.8,
则罚球10次得分为10×2×0.8=16,
∴估计他能得16分.
一.选择题
1.连续掷两枚质地均匀的硬币,则两枚硬币都正面朝上的概率为( )
A. B. C. D.
2.甲盒子中装有3个乒乓球,分别标号为1,2,3;乙盒子中装有2个乒乓球,分别标号为1,2.现从每个盒子中随机取出1个球,则取出的两球标号之和为4的概率是( )
A. B. C. D.
3.在一个不适明的发子中装有四个小球,它们除分别标有的号码5,6,7,8不同外,其他完全相同若任意从袋子中摸出一球后不放同,再任意从袋子中摸出一球,则第二次摸出球的号码与第一次换出球的号码的和等于15的概率是( )
A. B. C. D.
4.某区响应国家提出的垃圾分类的号召,将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其他垃圾四类,并分别设置了相应的垃圾箱.为了解居民生活垃圾分类的情况,随机对该区四类垃圾箱中总计1000吨生活垃圾进行分拣后,统计数据如表:
垃圾箱种类 垃圾量
垃圾种类(吨) “厨余垃圾”箱 “可回收物”箱 “有害垃圾”箱 “其他垃圾”箱
厨余垃圾 400 100 40 60
可回收物 30 140 10 20
有害垃圾 5 20 60 15
其他垃圾 25 15 20 40
下列三种说法:
(1)厨余垃圾投放错误的有400t;
(2)估计可回收物投放正确的概率约为;
(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普.
其中正确的个数是( )
A.0 B.1 C.2 D.3
5.在不透明的袋子里装有16个红球和若干个白球,这些球除颜色不同外无其它差别.每次从袋子里摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.6,则袋中白球有( )
A.12个 B.20个 C.24个 D.40个
6.在利用正六面体骰子进行频率估计概率的实验中,小颖同学统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( )
A.朝上的点数是5的概率
B.朝上的点数是奇数的概率
C.朝上的点数是大于2的概率
D.朝上的点数是3的倍数的概率
二.填空题
7.一个不透明的口袋中装有一红一白两个小球,它们除颜色外完全相同,从口袋中随机摸出1个小球,记下摸出小球的颜色后,放回口袋摇匀;再从口袋中随机摸出1个小球,记下摸出小球颜色后,放回口袋摇匀;第三次从口袋中随机摸出1个小球,则三次摸出的小球恰好颜色相同的概率为 .
8.从标有1,2,3,4的四张卡片中任取两张,卡片上的数字之和为奇数的概率是 .
9.从四张分别写着“中”“考”“加”“油”的卡片(大小、形状完全相同)中随机抽取两张,恰好是“加”“油”两字的概率是 .
10.一个不透明的布袋里装有100个只有颜色不同的球,这100个球中有m个红球.通过大量重复试验后发现,从布袋中随机摸出一个球摸到红球的频率稳定在0.2左右,则m的值约为 .
11.在一个不透明的口袋中装有5个红球和若干个白球,它们除颜色外其他完全相同,通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,则估计口袋中白球大约有 个.
三.解答题
12.某中学开展黄梅戏演唱比赛,组委会将本次比赛的成绩(单位:分)进行整理,并绘制成如下频数分布表和频数分布直方图(不完整).
成绩 频数 频率
50≤x<60 2 0.04
60≤x<70 a 0.16
70≤x<80 20 0.40
80≤x<90 16 0.32
90≤x≤100 4 b
合计 50 1
请你根据图表提供的信息,解答下列问题:
(1)求出a,b的值并补全频数分布直方图.
(2)将此次比赛成绩分为三组:A.50≤x<60;B.60≤x<80;C.80≤x≤100若按照这样的分组方式绘制扇形统计图,则其中C组所在扇形的圆心角的度数是多少?
(3)学校准备从不低于90分的参赛选手中任选2人参加市级黄梅戏演唱比赛,求都取得了95分的小欣和小怡同时被选上的概率.
13.在一个不透明的布袋中,有三个除颜色外其它均相同的小球,其中两个黑色,一个红色?
(1)请用表格或树状图求出:一次随机取出2个小球,颜色不同的概率.
(2)如果老师在布袋中加入若干个红色小球.然后小明通过做实验的方式猜测加入的小球数,小明每次摸出一个小球记录下慎色并放回,实验数据如下表:
实验次数 100 200 300 400 500 1000
摸出红球 78 147 228 304 373 752
请你帮小明算出老师放入了多少个红色小球.
14.小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问:小明正好穿的是相同的一双袜子的概率是多少?
15.目前“校园手机”现象越来越受到社会关注,针对这种现象,某校九年级数学兴趣小组的同学随机调查了若干名家长对“中学生带手机的”的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对).并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)在此次调查活动中,初三(1)班有A1、A2两位家长对中学生带手机持反对态度,初三(2)班有B1、B2两位学生家长对中学生带手机也持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求出选出的2人来自不同班级的概率.
16.在一个不透明袋子中装有1个红球,1个绿球和n个白球,这些球除颜色外均相同.
(1)从袋中随机摸出一个球,记录其颜色后放回,搅匀后再随机摸出一个球,经过大量重复该实验,发现摸到绿球的频率值稳定于0.2,则n的值是 ;
(2)当n=2时,从该不透明的袋子中一次摸出两个球,求摸出的两个球颜色不同的概率.(用“画树状图”或“列表”的方法写出分析过程)
17.在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只.某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
(1)请估计:当n很大时,摸到白球的频率将会接近 ;
(2)试估计口袋中黑、白两种颜色的球各有多少只?
(3)请画树状图或列表计算:从中先摸出一个球,不放回,再摸出一个球,这两只球颜色不同的概率是多少?
18.为了准备体育艺术节的比赛,某篮球运动员在进行定点罚球训练,如表是部分训练记录:
罚球次数 20 40 60 80 100 120
命中次数 15 32 48 65 80 96
命中频率 0.75 0.8 0.8 0.81 0.8 0.8
(1)根据上表:估计该运动员罚球命中的概率是 ;
(2)根据上表分析,如果该运动员在一次比赛中共获得10次罚球机会(每次罚球投掷2次,每命中一次得1分),估计他罚球能得多少分,请说明理由.
参考答案
一.选择题
1. A.
2. B.
3. D.
4. C.
5. C.
6. D.
二.填空题
7. .
8. .
9. .
10. 20.
11. 15.
三.解答题
12.解:(1)a=50×0.16=8,b==0.08,补图如下:
(2)A、50≤x<60的人数所占的百分比是:×100%=4%,
B、60≤x<80的人数所占的百分比是:×100%=56%,
C、80≤x<100的人数所占的百分比是:×100%=40%,画图如下:
C组所在扇形的圆心角的度数为360°×(0.32+0.08)=144°;
(3)由题意知,不低于9(0分)的学生共有4人,设这四名学生分别为M,X,A,B,其中小欣和小怡分别用A,B表示,根据题意,画树状图如下.
由树状图可知,共有12种等可能的结果,其中小欣和小怡同时被选上的结果有2种,
故小欣和小怡同时被选上的概率是.
13.解:(1)根据题意列表如下:
黑1 黑2 红
黑1 / (黑1,黑2) (黑1,红)
黑2 (黑2,黑1) / (黑2,红)
红 (红,黑1) (红,黑2) /
列表如图,一共有6种等可能事件,其中颜色不同的等可能事件有4种,
∴颜色不同的概率为P==;
(2)由图表可得摸到红球概率为,
设加入了x个红球,则=,
解得x=5,
经检验x=5是原方程的解,
答:加入了5个红球.
14.解:设两双袜子分别为黑色和白色,
画树状图得:
∵共有12种等可能的结果,两只恰好配成同色的一双有4种情况,
∴小明正好穿的是相同的一双袜子的概率=,
15.解:(1)120÷60%=200(人),
所以调查的家长数为200人;
(2)扇形C所对的圆心角的度数=360°×(1﹣20%﹣15%﹣60%)=18°,
C类的家长数=200×(1﹣20%﹣15%﹣60%)=10(人),
补充图为:
(3)设初三(1)班两名家长为A1、A2,初三(2)班两名家长为B1,B2,
画树状图为
共有12种等可能结果,其中2人来自不同班级共有8种,
所以2人来自不同班级的概率==.
16.解:(1)根据题意得:=0.2,
解得:n=3,
则n的值为3,
故答案为:3;
(2)根据题意画图如下:
共有12种等情况数,其中摸出的两个球颜色不同的有10种,
则摸出的两个球颜色不同的概率是=.
17.解:(1)根据图表给出的数据可得,当n很大时,摸到白球的频率将会接近0.6;
答案为:0.6;
(2)由(1)摸到白球的概率为0.6,所以可估计口袋中白种颜色的球的个数是:5×0.6=3(只),
黑颜色的球有5﹣3=2(只);
(3)画树状图为:
共有20种等可能的结果数,其中两只球颜色不同占12种,
所以两只球颜色不同的概率==.
18.解:(1)根据表格数据可知该运动员罚球命中的概率0.8,
故答案为0.8;
(2)由题意可知,罚球一次命中概率为0.8,
则罚球10次得分为10×2×0.8=16,
∴估计他能得16分.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
