华师大版七年级数学上学期《4.1 生活中的立体图形》同步练习卷(Word版 含答案)
文档属性
| 名称 | 华师大版七年级数学上学期《4.1 生活中的立体图形》同步练习卷(Word版 含答案) | 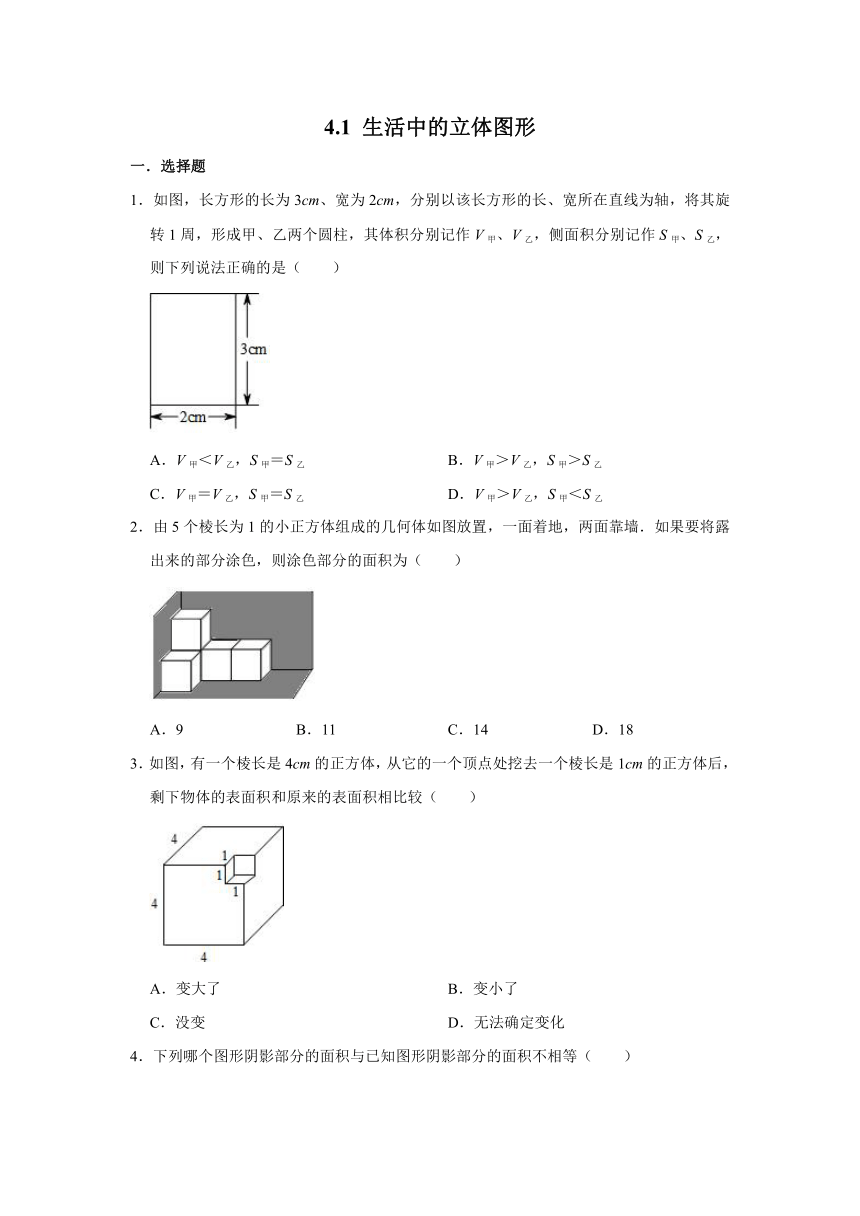 | |
| 格式 | doc | ||
| 文件大小 | 151.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-12 19:52:13 | ||
图片预览




文档简介
4.1 生活中的立体图形
一.选择题
1.如图,长方形的长为3cm、宽为2cm,分别以该长方形的长、宽所在直线为轴,将其旋转1周,形成甲、乙两个圆柱,其体积分别记作V甲、V乙,侧面积分别记作S甲、S乙,则下列说法正确的是( )
A.V甲<V乙,S甲=S乙 B.V甲>V乙,S甲>S乙
C.V甲=V乙,S甲=S乙 D.V甲>V乙,S甲<S乙
2.由5个棱长为1的小正方体组成的几何体如图放置,一面着地,两面靠墙.如果要将露出来的部分涂色,则涂色部分的面积为( )
A.9 B.11 C.14 D.18
3.如图,有一个棱长是4cm的正方体,从它的一个顶点处挖去一个棱长是1cm的正方体后,剩下物体的表面积和原来的表面积相比较( )
A.变大了 B.变小了
C.没变 D.无法确定变化
4.下列哪个图形阴影部分的面积与已知图形阴影部分的面积不相等( )
A. B. C. D.
5.小华用一罐黑漆和一罐白漆来漆一些立方体积木,他打算把这些立方体的每一面漆成单一的黑色或白色,如图1和图2是两种不同的漆法,但图2可以经过翻折得到图3,所以图2和图3是相同的漆法,那么他能漆成互不相同的立方体的种数是( )
A.10种 B.8种 C.9种 D.6种
6.围成下列立体图形的各个面中,每个面都是平的是( )
A.长方体 B.圆柱体
C.球体 D.圆锥体
7.如图:CD是直角三角形ABC的高,将直角三角形ABC按以下方式旋转一周可以得到右侧几何体的是( )
A.绕着AC旋转 B.绕着AB旋转 C.绕着CD旋转 D.绕着BC旋转
8.由7个相同的棱长为1的小立方块搭成的几何体如图所示,它的表面积为( )
A.23 B.24 C.26 D.28
9.棱长分别是3、5、8的三个正方体被粘合在一起,在这些用各种方式粘合在一起的几何体中,表面积最小的那个几何体的表面积是( )
A.570 B.502 C.530 D.538
10.一个立方体的体积为64立方米,将此立方体的棱长增加2米,那么新立方体的体积变为( )
A.72立方米 B.216立方米 C.66立方米 D.128立方米
11.一个正方体的表面涂满了颜色,按如图所示将它切成27个大小相等的小立方块,设其中仅有i个面(1,2,3)涂有颜色的小立方块的个数为xi,则x1、x2、x3之间的关系为( )
A.x1﹣x2+x3=1 B.x1+x2﹣x3=1 C.x1+x3﹣x2=2 D.x1﹣x3+x2=2
二.填空题
12.现在新型肺炎正在世界各地肆虐,WHO将它命名为冠状病毒2019(HCoV﹣19).它的形状是一个球体,体积大约288000πnm,则它的直径约是 nm.(球的体积公式V=)
13.如图,有一个盛有水的正方体玻璃容器,从内部量得它的棱长为30cm,容器内的水深为8cm,现把一块长,宽,高分别为15cm,10cm,10cm的长方体实心铁块平放进玻璃容器中,容器内的水将升高 cm.
14.如图,三个大小相同的球恰好放在一个圆柱形盒子里(球的半径为R时,球的体积为V=),若圆柱的容积为300π,则三个球的体积之和为 .(结果保留π)
15.圆规在纸上划过会留下一个封闭的痕迹,这种现象说明 “一个人手里拿着一个绑在一根棍上的半圆面,当这个人把这个半圆面绕着这根棍飞快旋转起来时就会看到一个球,这种现象说明 .
16.如图,有两个相同的长方体纸盒,它们的长、宽、高分别是12cm,6cm,2cm,现要用这两个纸盒搭成一个大长方体,搭成的大长方体的表面积最小为 cm2.
17.工人师傅按照“最优化处理”打包多个同一款式长方体纸盒,其“最优化处理”是指:每相邻的两个纸盒必须以完全一样的面对接,最后打包成一个表面积最小的长方体,已知长方体纸盒的长xcm、宽ycm、高zcm都为整数,且x>y>z>1,x+z=2y,x+y+z+xy+xz+yz+xyz=439,若将六个此款式纸盒按“最优化处理”打包,其表面积为 cm2.
三.解答题
18.一个长方体,如果它的长增加2厘米,体积就增加20立方厘米;如果宽加3厘米,体积增加60立方厘米;如果高增加5厘米,体积增加40厘米.求原来长方体的表面积.
19.按要求完成下题
(1)求圆柱的表面积和体积.(结果保留π)
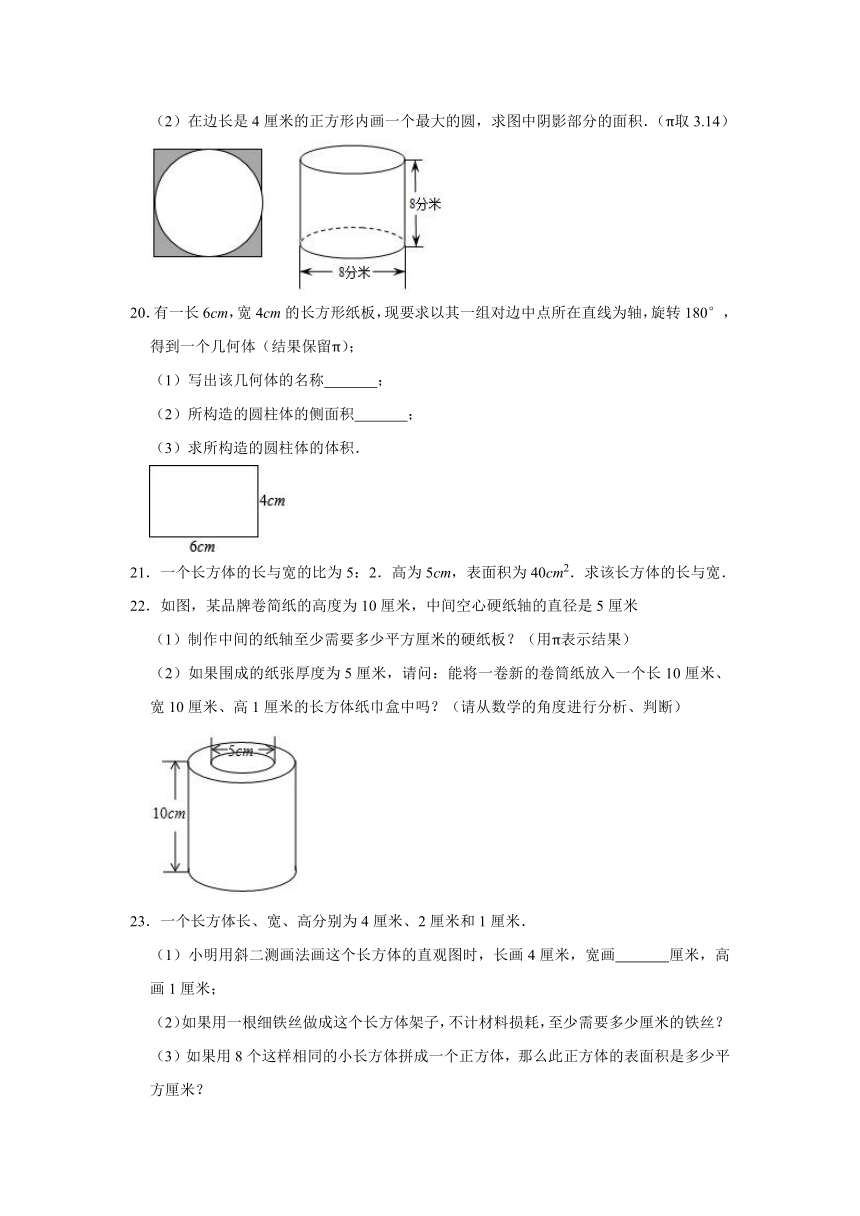
(2)在边长是4厘米的正方形内画一个最大的圆,求图中阴影部分的面积.(π取3.14)
20.有一长6cm,宽4cm的长方形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个几何体(结果保留π);
(1)写出该几何体的名称 ;
(2)所构造的圆柱体的侧面积 ;
(3)求所构造的圆柱体的体积.
21.一个长方体的长与宽的比为5:2.高为5cm,表面积为40cm2.求该长方体的长与宽.
22.如图,某品牌卷简纸的高度为10厘米,中间空心硬纸轴的直径是5厘米
(1)制作中间的纸轴至少需要多少平方厘米的硬纸板?(用π表示结果)
(2)如果围成的纸张厚度为5厘米,请问:能将一卷新的卷筒纸放入一个长10厘米、宽10厘米、高1厘米的长方体纸巾盒中吗?(请从数学的角度进行分析、判断)
23.一个长方体长、宽、高分别为4厘米、2厘米和1厘米.
(1)小明用斜二测画法画这个长方体的直观图时,长画4厘米,宽画 厘米,高画1厘米;
(2)如果用一根细铁丝做成这个长方体架子,不计材料损耗,至少需要多少厘米的铁丝?
(3)如果用8个这样相同的小长方体拼成一个正方体,那么此正方体的表面积是多少平方厘米?
24.12个棱长为1厘米的正方体叠在一起,成为一个长方体,求这个长方体的表面积.
25.已知:如图所示三棱柱,AB=8cm,BC=10cm,AC=6cm,∠BAC=90°,三棱柱高是15cm,求:该三棱柱的表面积.
26.棱长为a的正方体摆放成如图的形状,问:
(1)如图摆放成的几何体,共有几个正方体?表面积是多少?
(2)如果将正方体按如图的方式摆放4层,共有几个正方体?表面积是多少?
(3)若摆放成n层,那么几何体表面积又是多少.
参考答案
一.选择题
1. A.
2. B.
3. C.
4. D.
5. A.
6. A.
7. B.
8. D.
9. B.
10. B.
11. C.
二.填空题
12. 120
13. 1.6或1
14. 200π.
15.点动成线,面动成体.
16. 288.
17. 856.
三.解答题
18.解:(长×宽+长×高+高×宽)×2
=(8+10+20)×2
=76(平方厘米).
故这个长方体的表面积为76平方厘米.
19.解:(1)圆柱的表面积=8π×8+2?π?42=96π平方分米,圆柱的体积=π×42×8=108π立方分米;
(2)图中阴影部分的面积=4×4﹣π×22=16﹣4π≈3.44平方厘米.
20.解:(1)该几何体的名称为圆柱;
故答案为:圆柱;
(2)分两种情况:
以较长的一组对边中点所在直线为轴旋转,如图①,
所构造的圆柱体的侧面积为6π×4=24π(cm2);
以较短的一组对边中点所在直线为轴旋转,如图②,
所构造的圆柱体的侧面积为4π×6=24π(cm2),
综上所述,所构造的圆柱体的侧面积为24πcm2;
故答案为:24πcm2.
(3)分两种情况:
以较长的一组对边中点所在直线为轴旋转,所构造的圆柱体的体积为π×32×4=36π(cm3),
以较短的一组对边中点所在直线为轴旋转,所构造的圆柱体的体积为π×22×6=24π(cm3),
综上所述,所构造的圆柱体的体积为36πcm3或24πcm3.
21.解:设这个长方体的宽为2xcm,则长为5xcm,
依题意,得:2(5x?2x+5?5x+5?2x)=40,
整理,得:2x2+7x﹣4=0,
解得:x1=0.5,x2=﹣4(不合题意,舍去),
∴2x=1,5x=2.5.
答:这个长方体的长为2.5cm,宽为1cm.
22.解:(1)π×5×10=50π 平方厘米,
(2)不能,
∵围成的纸张厚度为5厘米,
∴一卷新的卷筒纸底面直径为15cm,
又∵长方体纸巾盒的长10厘米、宽10厘米、高1厘米,
∴不能放进去.
23.解:(1)几何体的直观图中,平行于x轴的线段的长度不变,而平行于y轴的线段的长度变为原来的一半,故宽画1厘米;
故答案为:1;
(2)4(4+2+1)=28(厘米),
故至少需要28厘米的铁丝;
(3)用8个这样相同的小长方体拼成一个正方体,其体积为8×4×2×1=64(立方厘米),故其棱长为4厘米,
∴此正方体的表面积是6×4×4=96(平方厘米).
24.解:①12×1×1拼法的长方体表面积:
(1×1+1×12+12×1)×2=50(平方厘米);
②6×2×1拼法的长方体表面积:
(6×2+6×1+2×1)×2=20×2=40(平方厘米);
③3×4×1拼法的长方体表面积:
(3×1+4×1+3×4)×2=38(平方厘米);
④3×2×2拼法的长方体表面积:
(3×2+3×2+2×2)×2=32(平方厘米);
答:这个长方体的表面积为50平方厘米或40平方厘米或38平方厘米或32平方厘米.
故答案为:2600或2200平方厘米
25.解:三棱柱的表面积×6×8×2+6×15+8×15+10×15=408厘米2.
故三棱柱的表面积为408厘米2.
26.解:(1)图中1+3+6=10个正方体,根据以上分析该物体的表面积为6×6a2=36a2.
(2)根据以上分析可得:如果将正方体按如图的方式摆放4层,则4层共有1+3+6+10=20个正方体,表面积为
(1+2+3+4)×6a2=60a2.
(3)由题意知,从正面看到的正方形个数有(1+2+3+4+…+n)=个,
表面积为:×6==3n(n+1)a2.
一.选择题
1.如图,长方形的长为3cm、宽为2cm,分别以该长方形的长、宽所在直线为轴,将其旋转1周,形成甲、乙两个圆柱,其体积分别记作V甲、V乙,侧面积分别记作S甲、S乙,则下列说法正确的是( )
A.V甲<V乙,S甲=S乙 B.V甲>V乙,S甲>S乙
C.V甲=V乙,S甲=S乙 D.V甲>V乙,S甲<S乙
2.由5个棱长为1的小正方体组成的几何体如图放置,一面着地,两面靠墙.如果要将露出来的部分涂色,则涂色部分的面积为( )
A.9 B.11 C.14 D.18
3.如图,有一个棱长是4cm的正方体,从它的一个顶点处挖去一个棱长是1cm的正方体后,剩下物体的表面积和原来的表面积相比较( )
A.变大了 B.变小了
C.没变 D.无法确定变化
4.下列哪个图形阴影部分的面积与已知图形阴影部分的面积不相等( )
A. B. C. D.
5.小华用一罐黑漆和一罐白漆来漆一些立方体积木,他打算把这些立方体的每一面漆成单一的黑色或白色,如图1和图2是两种不同的漆法,但图2可以经过翻折得到图3,所以图2和图3是相同的漆法,那么他能漆成互不相同的立方体的种数是( )
A.10种 B.8种 C.9种 D.6种
6.围成下列立体图形的各个面中,每个面都是平的是( )
A.长方体 B.圆柱体
C.球体 D.圆锥体
7.如图:CD是直角三角形ABC的高,将直角三角形ABC按以下方式旋转一周可以得到右侧几何体的是( )
A.绕着AC旋转 B.绕着AB旋转 C.绕着CD旋转 D.绕着BC旋转
8.由7个相同的棱长为1的小立方块搭成的几何体如图所示,它的表面积为( )
A.23 B.24 C.26 D.28
9.棱长分别是3、5、8的三个正方体被粘合在一起,在这些用各种方式粘合在一起的几何体中,表面积最小的那个几何体的表面积是( )
A.570 B.502 C.530 D.538
10.一个立方体的体积为64立方米,将此立方体的棱长增加2米,那么新立方体的体积变为( )
A.72立方米 B.216立方米 C.66立方米 D.128立方米
11.一个正方体的表面涂满了颜色,按如图所示将它切成27个大小相等的小立方块,设其中仅有i个面(1,2,3)涂有颜色的小立方块的个数为xi,则x1、x2、x3之间的关系为( )
A.x1﹣x2+x3=1 B.x1+x2﹣x3=1 C.x1+x3﹣x2=2 D.x1﹣x3+x2=2
二.填空题
12.现在新型肺炎正在世界各地肆虐,WHO将它命名为冠状病毒2019(HCoV﹣19).它的形状是一个球体,体积大约288000πnm,则它的直径约是 nm.(球的体积公式V=)
13.如图,有一个盛有水的正方体玻璃容器,从内部量得它的棱长为30cm,容器内的水深为8cm,现把一块长,宽,高分别为15cm,10cm,10cm的长方体实心铁块平放进玻璃容器中,容器内的水将升高 cm.
14.如图,三个大小相同的球恰好放在一个圆柱形盒子里(球的半径为R时,球的体积为V=),若圆柱的容积为300π,则三个球的体积之和为 .(结果保留π)
15.圆规在纸上划过会留下一个封闭的痕迹,这种现象说明 “一个人手里拿着一个绑在一根棍上的半圆面,当这个人把这个半圆面绕着这根棍飞快旋转起来时就会看到一个球,这种现象说明 .
16.如图,有两个相同的长方体纸盒,它们的长、宽、高分别是12cm,6cm,2cm,现要用这两个纸盒搭成一个大长方体,搭成的大长方体的表面积最小为 cm2.
17.工人师傅按照“最优化处理”打包多个同一款式长方体纸盒,其“最优化处理”是指:每相邻的两个纸盒必须以完全一样的面对接,最后打包成一个表面积最小的长方体,已知长方体纸盒的长xcm、宽ycm、高zcm都为整数,且x>y>z>1,x+z=2y,x+y+z+xy+xz+yz+xyz=439,若将六个此款式纸盒按“最优化处理”打包,其表面积为 cm2.
三.解答题
18.一个长方体,如果它的长增加2厘米,体积就增加20立方厘米;如果宽加3厘米,体积增加60立方厘米;如果高增加5厘米,体积增加40厘米.求原来长方体的表面积.
19.按要求完成下题
(1)求圆柱的表面积和体积.(结果保留π)
(2)在边长是4厘米的正方形内画一个最大的圆,求图中阴影部分的面积.(π取3.14)
20.有一长6cm,宽4cm的长方形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个几何体(结果保留π);
(1)写出该几何体的名称 ;
(2)所构造的圆柱体的侧面积 ;
(3)求所构造的圆柱体的体积.
21.一个长方体的长与宽的比为5:2.高为5cm,表面积为40cm2.求该长方体的长与宽.
22.如图,某品牌卷简纸的高度为10厘米,中间空心硬纸轴的直径是5厘米
(1)制作中间的纸轴至少需要多少平方厘米的硬纸板?(用π表示结果)
(2)如果围成的纸张厚度为5厘米,请问:能将一卷新的卷筒纸放入一个长10厘米、宽10厘米、高1厘米的长方体纸巾盒中吗?(请从数学的角度进行分析、判断)
23.一个长方体长、宽、高分别为4厘米、2厘米和1厘米.
(1)小明用斜二测画法画这个长方体的直观图时,长画4厘米,宽画 厘米,高画1厘米;
(2)如果用一根细铁丝做成这个长方体架子,不计材料损耗,至少需要多少厘米的铁丝?
(3)如果用8个这样相同的小长方体拼成一个正方体,那么此正方体的表面积是多少平方厘米?
24.12个棱长为1厘米的正方体叠在一起,成为一个长方体,求这个长方体的表面积.
25.已知:如图所示三棱柱,AB=8cm,BC=10cm,AC=6cm,∠BAC=90°,三棱柱高是15cm,求:该三棱柱的表面积.
26.棱长为a的正方体摆放成如图的形状,问:
(1)如图摆放成的几何体,共有几个正方体?表面积是多少?
(2)如果将正方体按如图的方式摆放4层,共有几个正方体?表面积是多少?
(3)若摆放成n层,那么几何体表面积又是多少.
参考答案
一.选择题
1. A.
2. B.
3. C.
4. D.
5. A.
6. A.
7. B.
8. D.
9. B.
10. B.
11. C.
二.填空题
12. 120
13. 1.6或1
14. 200π.
15.点动成线,面动成体.
16. 288.
17. 856.
三.解答题
18.解:(长×宽+长×高+高×宽)×2
=(8+10+20)×2
=76(平方厘米).
故这个长方体的表面积为76平方厘米.
19.解:(1)圆柱的表面积=8π×8+2?π?42=96π平方分米,圆柱的体积=π×42×8=108π立方分米;
(2)图中阴影部分的面积=4×4﹣π×22=16﹣4π≈3.44平方厘米.
20.解:(1)该几何体的名称为圆柱;
故答案为:圆柱;
(2)分两种情况:
以较长的一组对边中点所在直线为轴旋转,如图①,
所构造的圆柱体的侧面积为6π×4=24π(cm2);
以较短的一组对边中点所在直线为轴旋转,如图②,
所构造的圆柱体的侧面积为4π×6=24π(cm2),
综上所述,所构造的圆柱体的侧面积为24πcm2;
故答案为:24πcm2.
(3)分两种情况:
以较长的一组对边中点所在直线为轴旋转,所构造的圆柱体的体积为π×32×4=36π(cm3),
以较短的一组对边中点所在直线为轴旋转,所构造的圆柱体的体积为π×22×6=24π(cm3),
综上所述,所构造的圆柱体的体积为36πcm3或24πcm3.
21.解:设这个长方体的宽为2xcm,则长为5xcm,
依题意,得:2(5x?2x+5?5x+5?2x)=40,
整理,得:2x2+7x﹣4=0,
解得:x1=0.5,x2=﹣4(不合题意,舍去),
∴2x=1,5x=2.5.
答:这个长方体的长为2.5cm,宽为1cm.
22.解:(1)π×5×10=50π 平方厘米,
(2)不能,
∵围成的纸张厚度为5厘米,
∴一卷新的卷筒纸底面直径为15cm,
又∵长方体纸巾盒的长10厘米、宽10厘米、高1厘米,
∴不能放进去.
23.解:(1)几何体的直观图中,平行于x轴的线段的长度不变,而平行于y轴的线段的长度变为原来的一半,故宽画1厘米;
故答案为:1;
(2)4(4+2+1)=28(厘米),
故至少需要28厘米的铁丝;
(3)用8个这样相同的小长方体拼成一个正方体,其体积为8×4×2×1=64(立方厘米),故其棱长为4厘米,
∴此正方体的表面积是6×4×4=96(平方厘米).
24.解:①12×1×1拼法的长方体表面积:
(1×1+1×12+12×1)×2=50(平方厘米);
②6×2×1拼法的长方体表面积:
(6×2+6×1+2×1)×2=20×2=40(平方厘米);
③3×4×1拼法的长方体表面积:
(3×1+4×1+3×4)×2=38(平方厘米);
④3×2×2拼法的长方体表面积:
(3×2+3×2+2×2)×2=32(平方厘米);
答:这个长方体的表面积为50平方厘米或40平方厘米或38平方厘米或32平方厘米.
故答案为:2600或2200平方厘米
25.解:三棱柱的表面积×6×8×2+6×15+8×15+10×15=408厘米2.
故三棱柱的表面积为408厘米2.
26.解:(1)图中1+3+6=10个正方体,根据以上分析该物体的表面积为6×6a2=36a2.
(2)根据以上分析可得:如果将正方体按如图的方式摆放4层,则4层共有1+3+6+10=20个正方体,表面积为
(1+2+3+4)×6a2=60a2.
(3)由题意知,从正面看到的正方形个数有(1+2+3+4+…+n)=个,
表面积为:×6==3n(n+1)a2.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
