青岛版八年级数学上册 1.2《怎样判定三角形全等》课件(共17张PPT)
文档属性
| 名称 | 青岛版八年级数学上册 1.2《怎样判定三角形全等》课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 707.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-13 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
青岛版八年级数学上册
怎样判定三角形全等
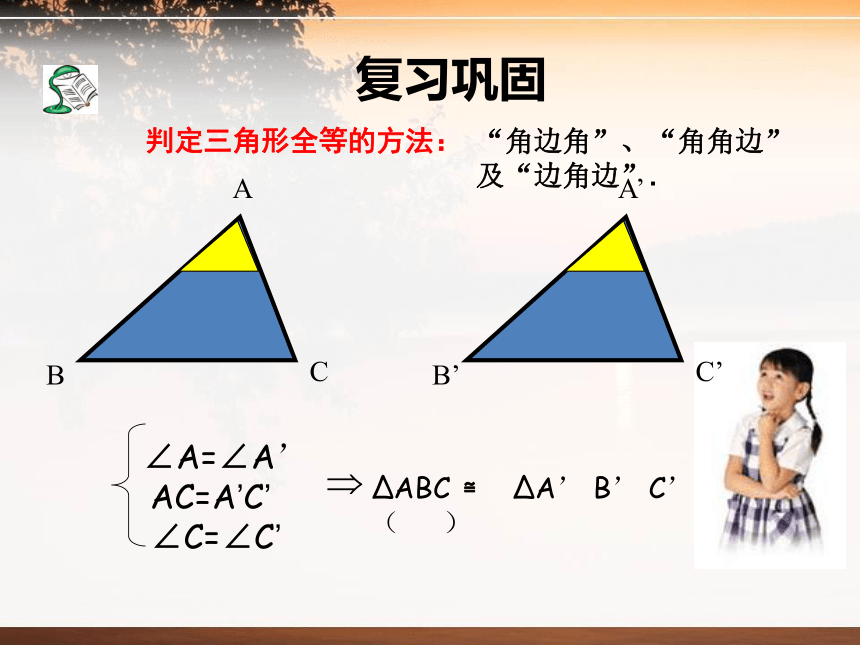
复习巩固
判定三角形全等的方法:
A
B
C
A’
B’
C’
ΔABC
≌
?A’
B’
C’(
)
∠A=∠A’
AC=A’C’
∠C=∠C’
“角边角”、“角角边”及“边角边”.
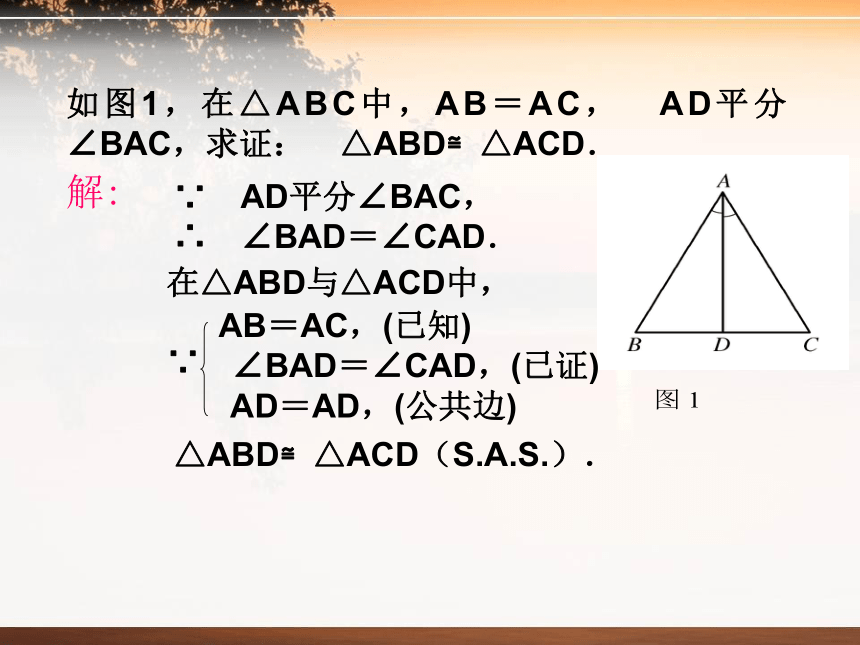
如图1,在△ABC中,AB=AC, AD平分∠BAC,求证: △ABD≌△ACD.
解:
∵ AD平分∠BAC,
∴ ∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,(已知)
∠BAD=∠CAD,(已证)
AD=AD,(公共边)
△ABD≌△ACD(S.A.S.).
∵
PPT模板:www.1ppt.com/moban/
PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/
PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/
PPT教程:
www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/
范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/
教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn
PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/
数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/
美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/
物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/
生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/
历史课件:www.1ppt.com/kejian/lishi/
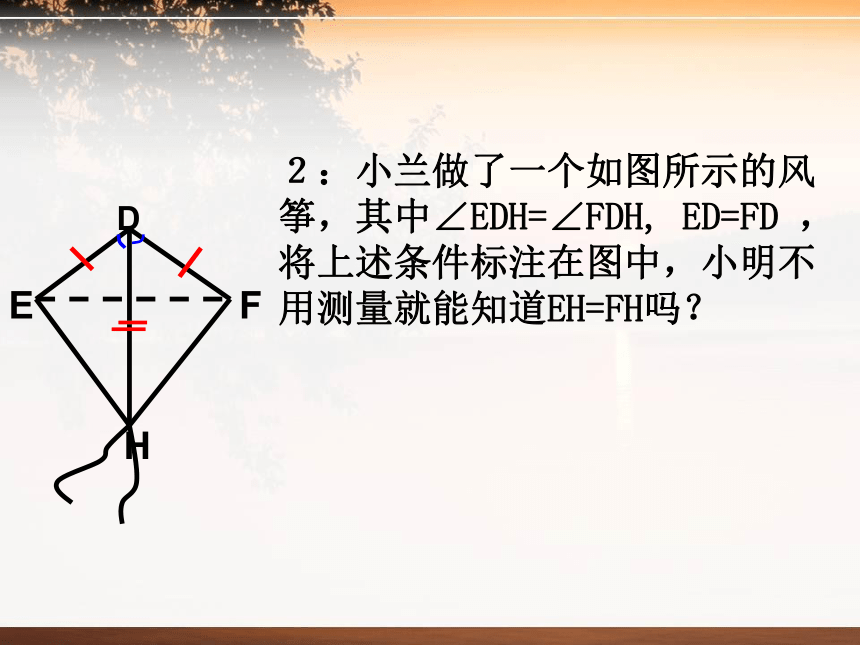
2:小兰做了一个如图所示的风筝,其中∠EDH=∠FDH,
ED=FD
,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?
E
F
D
H
1、用三根木条制作一个三角形的架子?,在用四根木条钉一个四边形的架子?,分
别拉动架子?和?的边框,你有什么发现?
2、如果再取与架子?的三根木条分别相等的木条,再制作一个三角形的架子?,这
两个三角形的架子形状、大小相同吗?如果把其中一个三角形架子叠放在另一个三角形架子上,它们能重合吗?
3、通过以上实验,你能得出什么结论?
试验与探究
结论:由于拥有对应相等三边的所有三角形将全等,所以只要三条边长度固定,这个三角形的形状大小就完全确定,所以三角形具有稳定性,而四边形不具备这样的性质,四边形具有不稳定性。三角形稳定性和四边形的不稳定性在生活及生产实际中都很有用处。
试验与探究
实验与探究
a
b
c
实验与探究
用符号语言表达为:
在△ABC与△
A′B′C′中:
∵AB=A′B′,AC=A′C′,BC=
B′C′
∴△ABC≌△
A′B′C′(SSS)
A
B
C
A′
B′
C′
判定方法4:三边分别相等的两个三角形全等
小结:欲证角相等,转化为证三角形全等。
例5:如图,已知AD=CB,AB=CD,那么∠A=∠C吗??为什么?
拓展练习
如图,已知AB=CD,AD=CB,说明:∠B=∠D
证明:连结AC,
AB=CD(已知)
AC=AC(公用边)
BC=AD(已知)
∴
△
ABC≌
△
CDA(SSS)
∴
∠B=∠D(全等三角形对应角相等)
问:此题添加辅助线,若连结BD行吗?
在原有条件下,还能推出什么结论?
答:∠ABC=∠ADC,AB∥CD,AD∥BC
A
B
C
D
A
B
C
D
在△ABC和△
ADC中
小结:四边形问题转化为三角形问题解决。
例6、如图,已知AB=DE
BC=DF,AE=CF。
1)AC与EF相等吗?为什么?
2)指出
△ABC和△EDF中互相平行的边,并说明理由。
F
B
A
E
C
D
∵AE=CF
∴
AE+EC=CF+EC
∴AC=EF
在△ABC和△EDF中
AB=ED(已知)
BC=DF(已知)
AC=EF(已证)
∴△ABC≌△EDF(SSS)
∴∠A=∠DEF,∠ACB=∠EFD
∴AB∥ED,BC∥DF.
三个角分别对应相等的两个三角形是否全等?
判定两个三角形全等,至少要有一条边对应相等.
实验与探究
通过这节课的学习你有什么收获?
小
结
判定方法4:三边分别相等的两个三角形全等
当堂检测
1
1
2
第1题图
第2题图
青岛版八年级数学上册
怎样判定三角形全等
复习巩固
判定三角形全等的方法:
A
B
C
A’
B’
C’
ΔABC
≌
?A’
B’
C’(
)
∠A=∠A’
AC=A’C’
∠C=∠C’
“角边角”、“角角边”及“边角边”.
如图1,在△ABC中,AB=AC, AD平分∠BAC,求证: △ABD≌△ACD.
解:
∵ AD平分∠BAC,
∴ ∠BAD=∠CAD.
在△ABD与△ACD中,
AB=AC,(已知)
∠BAD=∠CAD,(已证)
AD=AD,(公共边)
△ABD≌△ACD(S.A.S.).
∵
PPT模板:www.1ppt.com/moban/
PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/
PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/
PPT教程:
www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/
范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/
教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn
PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/
数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/
美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/
物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/
生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/
历史课件:www.1ppt.com/kejian/lishi/
2:小兰做了一个如图所示的风筝,其中∠EDH=∠FDH,
ED=FD
,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?
E
F
D
H
1、用三根木条制作一个三角形的架子?,在用四根木条钉一个四边形的架子?,分
别拉动架子?和?的边框,你有什么发现?
2、如果再取与架子?的三根木条分别相等的木条,再制作一个三角形的架子?,这
两个三角形的架子形状、大小相同吗?如果把其中一个三角形架子叠放在另一个三角形架子上,它们能重合吗?
3、通过以上实验,你能得出什么结论?
试验与探究
结论:由于拥有对应相等三边的所有三角形将全等,所以只要三条边长度固定,这个三角形的形状大小就完全确定,所以三角形具有稳定性,而四边形不具备这样的性质,四边形具有不稳定性。三角形稳定性和四边形的不稳定性在生活及生产实际中都很有用处。
试验与探究
实验与探究
a
b
c
实验与探究
用符号语言表达为:
在△ABC与△
A′B′C′中:
∵AB=A′B′,AC=A′C′,BC=
B′C′
∴△ABC≌△
A′B′C′(SSS)
A
B
C
A′
B′
C′
判定方法4:三边分别相等的两个三角形全等
小结:欲证角相等,转化为证三角形全等。
例5:如图,已知AD=CB,AB=CD,那么∠A=∠C吗??为什么?
拓展练习
如图,已知AB=CD,AD=CB,说明:∠B=∠D
证明:连结AC,
AB=CD(已知)
AC=AC(公用边)
BC=AD(已知)
∴
△
ABC≌
△
CDA(SSS)
∴
∠B=∠D(全等三角形对应角相等)
问:此题添加辅助线,若连结BD行吗?
在原有条件下,还能推出什么结论?
答:∠ABC=∠ADC,AB∥CD,AD∥BC
A
B
C
D
A
B
C
D
在△ABC和△
ADC中
小结:四边形问题转化为三角形问题解决。
例6、如图,已知AB=DE
BC=DF,AE=CF。
1)AC与EF相等吗?为什么?
2)指出
△ABC和△EDF中互相平行的边,并说明理由。
F
B
A
E
C
D
∵AE=CF
∴
AE+EC=CF+EC
∴AC=EF
在△ABC和△EDF中
AB=ED(已知)
BC=DF(已知)
AC=EF(已证)
∴△ABC≌△EDF(SSS)
∴∠A=∠DEF,∠ACB=∠EFD
∴AB∥ED,BC∥DF.
三个角分别对应相等的两个三角形是否全等?
判定两个三角形全等,至少要有一条边对应相等.
实验与探究
通过这节课的学习你有什么收获?
小
结
判定方法4:三边分别相等的两个三角形全等
当堂检测
1
1
2
第1题图
第2题图
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
