北师大版九年级数学下册课件:1.6 利用三角函数测高(20张)
文档属性
| 名称 | 北师大版九年级数学下册课件:1.6 利用三角函数测高(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-14 09:55:49 | ||
图片预览





文档简介
(共20张PPT)
第一章
直角三角形的边角关系
1.6
利用三角函数测高
情景导入
如果不告诉你这些高楼大厦的高度,你能想到办法测出它们的高度吗?
获取新知
活动一:使用侧倾器测量倾斜角
1.测倾器的组成:度盘、铅锤和支杆.
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
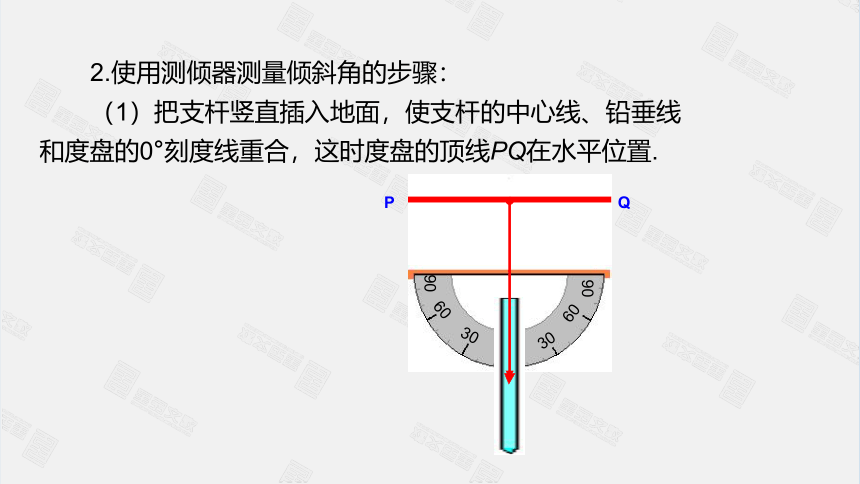
2.使用测倾器测量倾斜角的步骤:
(1)把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
0
30
30
60
60
90
90
P
Q
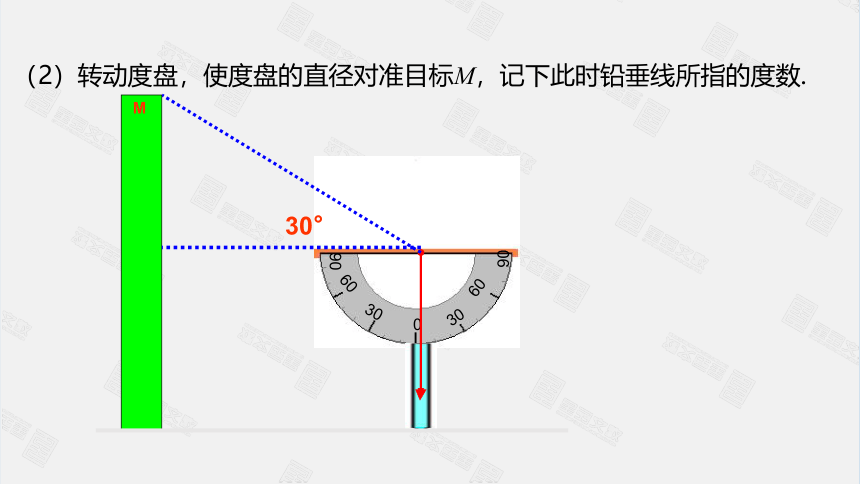
(2)转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
0
30
30
60
60
06
90
M
30°
活动二:测量底部可以到达的物体的高度
所谓"底部可以到达",就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
如图,要测量物体MN的高度,
可以按下列步骤进行:
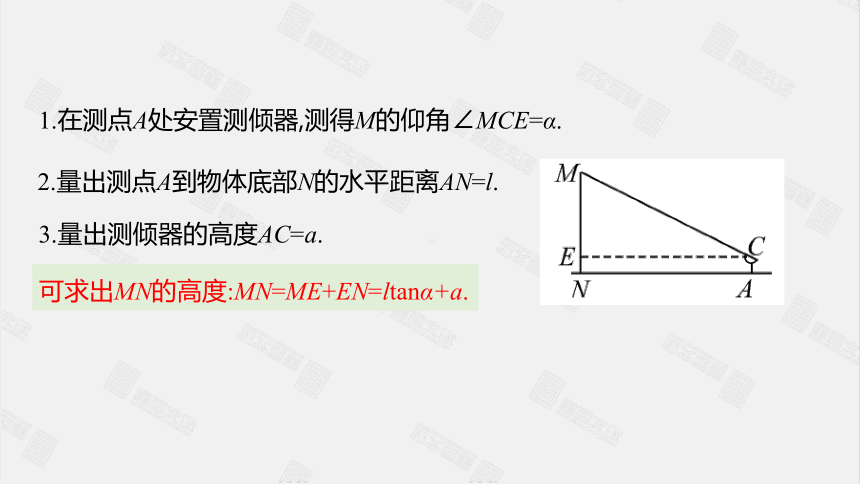
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=l.
3.量出测倾器的高度AC=a.
可求出MN的高度:MN=ME+EN=ltanα+a.
例题讲解
例1
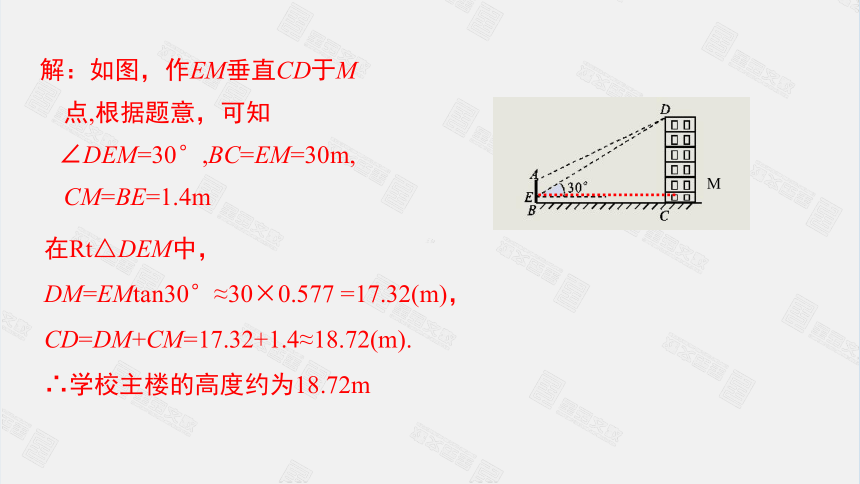
如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度(精确到0.01m).
解:如图,作EM垂直CD于M点,根据题意,可知
∠DEM=30°,BC=EM=30m,
CM=BE=1.4m
在Rt△DEM中,
DM=EMtan30°≈30×0.577
=17.32(m),
CD=DM+CM=17.32+1.4≈18.72(m).
∴学校主楼的高度约为18.72m
M
获取新知
活动三:测量底部不可以到达的物体的高度
所谓"底部不可以到达",就是在地面上不能直接测得测点与被测物体的底部之间的距离.如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.在测点B处安置测倾器,测得M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及A,B之间的距离AB=b.
则CD=AB=CE-DE=
=b
∴ME=
∴MN=
例题讲解
课题
在平面上测量地王大厦的高AB
测量示意图
测得数据
(测倾器高度为1m)
测量项目
∠α
∠β
CD的长
第一次
30°
16'
45°
35'
60.11m
第二次
29°
44'
44°
25’'
59.89m
平均值
例2
下表是小亮所填实习报告的部分内容,请根据数据求大楼的高.
C
E
D
F
A
G
B
α
β
30°
45°
60m
解:由表格中数据,得α=30°
,β=45°
,
答:大楼高度为
.
随堂演练
1.
如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30
m的B处测得树顶点A的仰角∠ABO为∠α,则树OA的高度为( )
A.
m
B.30sinα
m
C.30tanα
m
D.30cosα
m
C
2.
如图,在高度是21
m的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=________m(结果保留根号).
3.
如图,一枚运载火箭从距雷达站C处5
km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.求A,B两点间的距离.
(结果精确到0.1
km,参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
解:由题意,得∠AOC=90°,OC=5
km.
在Rt△AOC中,∵tan34°=
,
∴OA=OC·tan34°≈5×0.67=3.35(km).
在Rt△BOC中,∠BCO=45°,
∴OB=OC=5
km,
∴AB=OB-OA≈5-3.35=1.65≈1.7(km).
答:A,B两点间的距离约为1.7
km.
4.
如图小山岗的斜坡AC的坡度是
坡角为α,在与山脚C距离200
m的点D处测得山顶A的仰角为26.6°,求小山岗的高.(结果精确到1
m,参考数据:sin
26.6°≈0.45,cos
26.6°≈0.89,
tan
26.6°≈0.50)
解:设小山岗的高为x
m,
在Rt△ABC中,由题意得
tan
α=
∴BC=
∴BD=DC+BC=
在Rt△ABD中,tan
∠ADB=tan
26.6°=
∴
解得x≈300,即小山岗的高约为300
m.
课堂小结
利用三角函数测高
测倾器的认识及使用
测量底部可以到达的物体的高度(一次测量仰角)
测量底部不可以到达的物体的高度(两次测量仰角)
利用解三角形的知识,求出物体的高度
第一章
直角三角形的边角关系
1.6
利用三角函数测高
情景导入
如果不告诉你这些高楼大厦的高度,你能想到办法测出它们的高度吗?
获取新知
活动一:使用侧倾器测量倾斜角
1.测倾器的组成:度盘、铅锤和支杆.
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
2.使用测倾器测量倾斜角的步骤:
(1)把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
0
30
30
60
60
90
90
P
Q
(2)转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
0
30
30
60
60
06
90
M
30°
活动二:测量底部可以到达的物体的高度
所谓"底部可以到达",就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
如图,要测量物体MN的高度,
可以按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=l.
3.量出测倾器的高度AC=a.
可求出MN的高度:MN=ME+EN=ltanα+a.
例题讲解
例1
如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度(精确到0.01m).
解:如图,作EM垂直CD于M点,根据题意,可知
∠DEM=30°,BC=EM=30m,
CM=BE=1.4m
在Rt△DEM中,
DM=EMtan30°≈30×0.577
=17.32(m),
CD=DM+CM=17.32+1.4≈18.72(m).
∴学校主楼的高度约为18.72m
M
获取新知
活动三:测量底部不可以到达的物体的高度
所谓"底部不可以到达",就是在地面上不能直接测得测点与被测物体的底部之间的距离.如图,要测量物体MN的高度,可以按下列步骤进行:
1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.在测点B处安置测倾器,测得M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及A,B之间的距离AB=b.
则CD=AB=CE-DE=
=b
∴ME=
∴MN=
例题讲解
课题
在平面上测量地王大厦的高AB
测量示意图
测得数据
(测倾器高度为1m)
测量项目
∠α
∠β
CD的长
第一次
30°
16'
45°
35'
60.11m
第二次
29°
44'
44°
25’'
59.89m
平均值
例2
下表是小亮所填实习报告的部分内容,请根据数据求大楼的高.
C
E
D
F
A
G
B
α
β
30°
45°
60m
解:由表格中数据,得α=30°
,β=45°
,
答:大楼高度为
.
随堂演练
1.
如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30
m的B处测得树顶点A的仰角∠ABO为∠α,则树OA的高度为( )
A.
m
B.30sinα
m
C.30tanα
m
D.30cosα
m
C
2.
如图,在高度是21
m的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=________m(结果保留根号).
3.
如图,一枚运载火箭从距雷达站C处5
km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.求A,B两点间的距离.
(结果精确到0.1
km,参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
解:由题意,得∠AOC=90°,OC=5
km.
在Rt△AOC中,∵tan34°=
,
∴OA=OC·tan34°≈5×0.67=3.35(km).
在Rt△BOC中,∠BCO=45°,
∴OB=OC=5
km,
∴AB=OB-OA≈5-3.35=1.65≈1.7(km).
答:A,B两点间的距离约为1.7
km.
4.
如图小山岗的斜坡AC的坡度是
坡角为α,在与山脚C距离200
m的点D处测得山顶A的仰角为26.6°,求小山岗的高.(结果精确到1
m,参考数据:sin
26.6°≈0.45,cos
26.6°≈0.89,
tan
26.6°≈0.50)
解:设小山岗的高为x
m,
在Rt△ABC中,由题意得
tan
α=
∴BC=
∴BD=DC+BC=
在Rt△ABD中,tan
∠ADB=tan
26.6°=
∴
解得x≈300,即小山岗的高约为300
m.
课堂小结
利用三角函数测高
测倾器的认识及使用
测量底部可以到达的物体的高度(一次测量仰角)
测量底部不可以到达的物体的高度(两次测量仰角)
利用解三角形的知识,求出物体的高度
