华东师大版数学八年级上册 13.5.2线段垂直平分线课件(共18张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.5.2线段垂直平分线课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 325.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-15 10:36:38 | ||
图片预览


文档简介
(共18张PPT)
13.5.2
线段垂直平分线
高
速
公
路
A
B
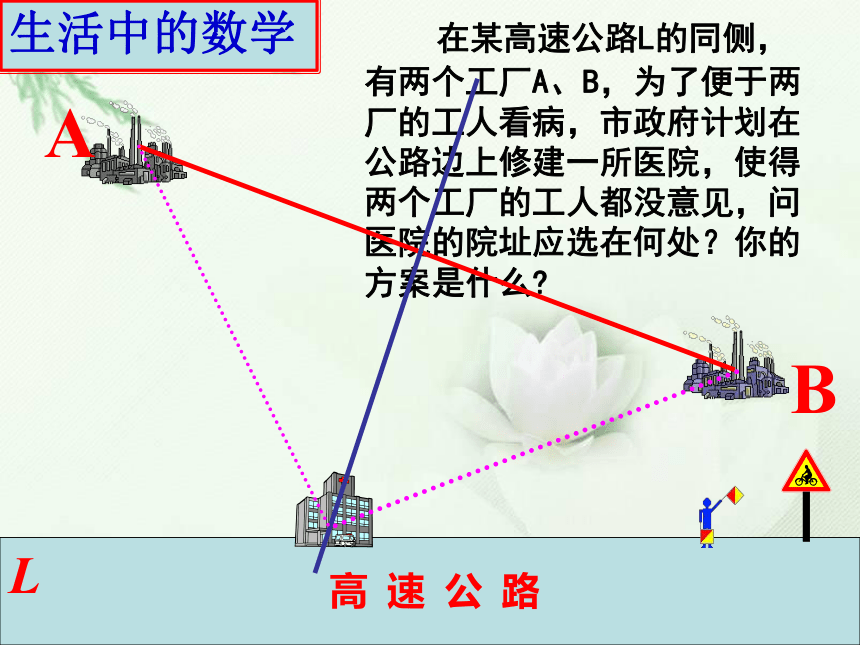
在某高速公路L的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?你的方案是什么?
生活中的数学
L
学习目标
1、使学生理解线段垂直平分线的性质定理及
逆定理,掌握这两个定理的关系并会用这两个定
理解决有关几何问题。
2、了解线段垂直平分线的证明过程。
3、结合教学内容培养学生的抽象思维能力。
学习重难点
重点:线段垂直平分线性质定理及逆定理的引入
证明及运用。
难点:线段垂直平分线性质定理及逆定理的关系。
回顾
1.等腰三角形有哪些性质?
N
A
B
P
M
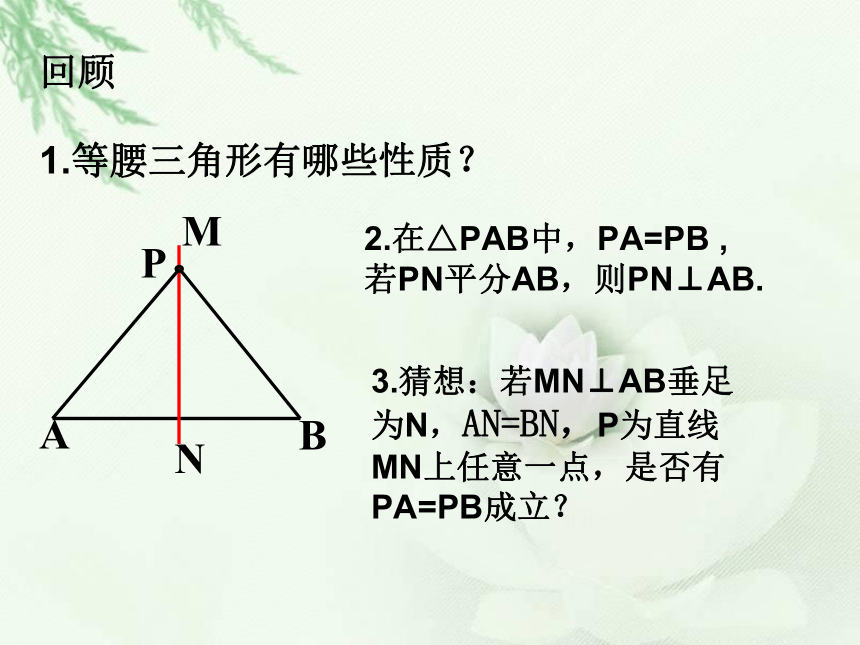
2.在△PAB中,PA=PB
,若PN平分AB,则PN⊥AB.
3.猜想:若MN⊥AB垂足为N,AN=BN,P为直线MN上任意一点,是否有PA=PB成立?
N
A
B
P
M
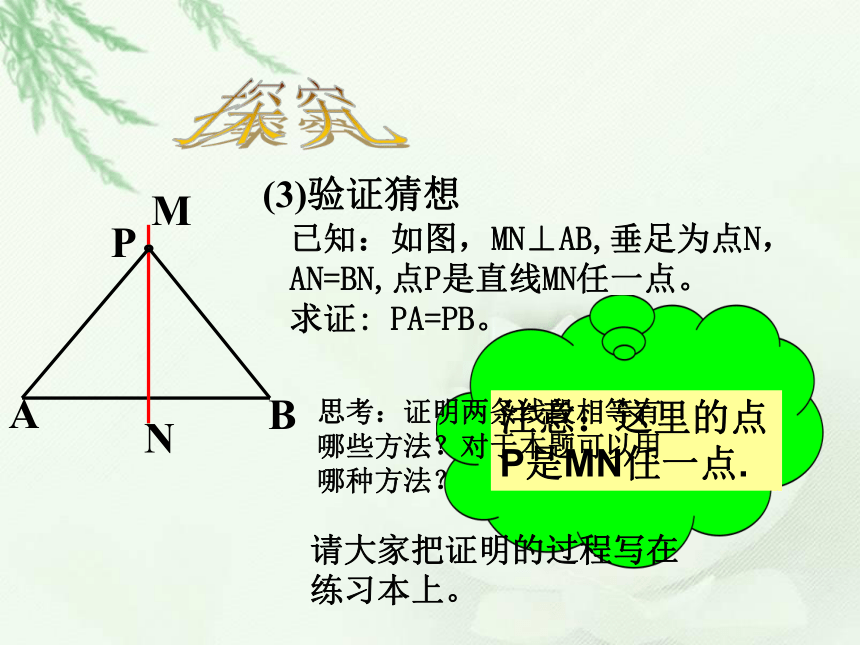
(3)验证猜想
已知:如图,MN⊥AB,垂足为点N,AN=BN,点P是直线MN任一点。
求证:
PA=PB。
注意:这里的点P是MN任一点.
思考:证明两条线段相等有哪些方法?对于本题可以用哪种方法?
请大家把证明的过程写在练习本上。
探究
(4)得出结论
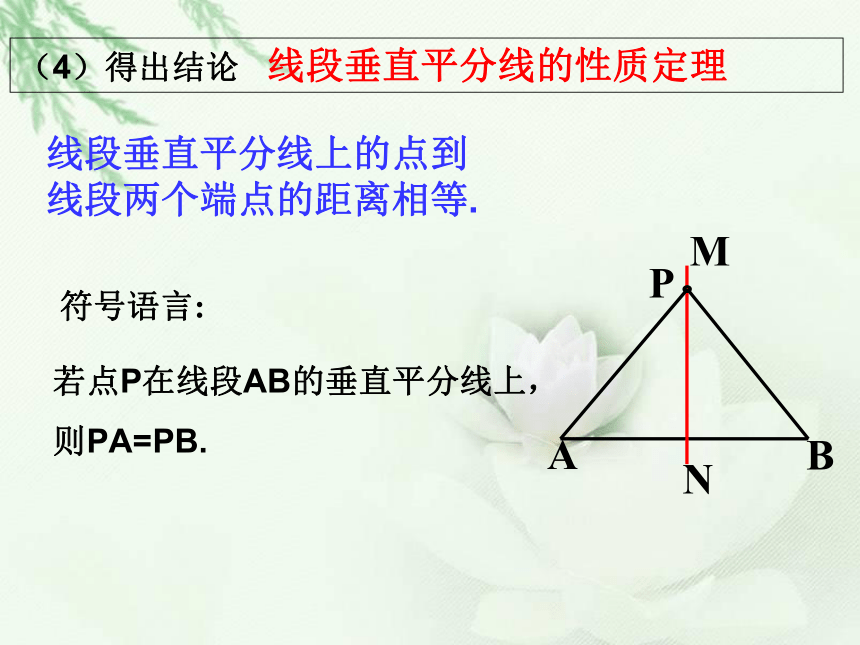
线段垂直平分线的性质定理
线段垂直平分线上的点到线段两个端点的距离相等.
符号语言:
若点P在线段AB的垂直平分线上,
则PA=PB.
N
A
B
P
M
线段垂直平分线上的点到线段两个端点的距离相等.
你能根据图形写出已知、求证,并进行证明吗?
如果有一个点在线段的垂直平分线上,那么这个点到线段的两个端点距离相等.
到线段的两个端点距离相等的点,在线段的垂直平分线上.
逆命题
P
A
B
若PA=PB,则点P在线段AB的垂直平分线上.
已知:PA=PB
求证:点P在线段AB的垂直平分线上.
证明:
过点P作AB的垂线PN,
垂足为C
∵PA=PB,PC⊥AB
∴PC平分AB
∴直线PN是线段AB的垂直平分线
即点P在AB的垂直平分线上
P
A
B
N
C
例题讲解
驶向胜利的彼岸
例1
如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED=
cm;如果∠ECD=600,那么∠EDC=
0.
老师期望:
你能说出填空结果的根据.
E
D
A
B
C
7
60
驶向胜利的彼岸
例2.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长.
老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去.
B
A
E
D
C
解:∵DE是AB的垂直平分线
∴EA=EB
∵△BCE的周长=EB+EC+BC=50
∴EA+EC+BC=50
即AC+BC=50
∵AC=27
∴BC=23
1.在△ABC中,∠ACB=90°,AB=8cm,BC的垂直平分线DE交AB于D点,则CD=____
4cm
2、在△ABC,PM,QN分别垂直平分AB,AC,则:
(1)若BC=10cm则△APQ的周长=_____cm;
(2)若∠BAC=100°则∠PAQ=______.
10
200
拿出准备好的三角形纸片,用折叠的方法找出每条边的垂直平分线。
思考:刚刚折出来的三条垂直平分线有什么关系?
画—个任意的三角形,并利用直尺和圆规作出三角形三条边的垂直平分线,要注意作图的方法和步骤。
观察作出来的三条垂直平分线有什么特点?对照纸折的三条垂直平分线,是不是它们共有的特点?
三角形三边的垂直平分线交与一点。
结论
如图,△ABC中,边AB、BC的垂直平分线交于点O。
(1)求证:OA=OB=OC。
(2)点O是否也在边AC的垂直平分线上呢?由此你能得出什么结论?
A
P
C
B
证明:∵点O在线段AB的垂直平分线上
∴OA=OB
∵点O在线段BC的垂直平分线上
∴OB=OC
∴OA=OB
∴点O在线段AC的垂直平分线上
3、在△ABC中,AB=AC,AB的中垂线与AC所在的直线相交所得的锐角为50°,则∠B=______.
700或200
例题:
有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。
A
B
C
高
速
公
路
A
B
在某高速公路L的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?你的方案是什么?
生活中的数学
L
课堂小结
本节课学习了哪些知识?
到线段的两端距离相等的点在线段的垂直平分线上.
线段的垂直平分线上的点到线段两个端点的距离相等.
作业
课本第99页习题13.5
第2、3题
13.5.2
线段垂直平分线
高
速
公
路
A
B
在某高速公路L的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?你的方案是什么?
生活中的数学
L
学习目标
1、使学生理解线段垂直平分线的性质定理及
逆定理,掌握这两个定理的关系并会用这两个定
理解决有关几何问题。
2、了解线段垂直平分线的证明过程。
3、结合教学内容培养学生的抽象思维能力。
学习重难点
重点:线段垂直平分线性质定理及逆定理的引入
证明及运用。
难点:线段垂直平分线性质定理及逆定理的关系。
回顾
1.等腰三角形有哪些性质?
N
A
B
P
M
2.在△PAB中,PA=PB
,若PN平分AB,则PN⊥AB.
3.猜想:若MN⊥AB垂足为N,AN=BN,P为直线MN上任意一点,是否有PA=PB成立?
N
A
B
P
M
(3)验证猜想
已知:如图,MN⊥AB,垂足为点N,AN=BN,点P是直线MN任一点。
求证:
PA=PB。
注意:这里的点P是MN任一点.
思考:证明两条线段相等有哪些方法?对于本题可以用哪种方法?
请大家把证明的过程写在练习本上。
探究
(4)得出结论
线段垂直平分线的性质定理
线段垂直平分线上的点到线段两个端点的距离相等.
符号语言:
若点P在线段AB的垂直平分线上,
则PA=PB.
N
A
B
P
M
线段垂直平分线上的点到线段两个端点的距离相等.
你能根据图形写出已知、求证,并进行证明吗?
如果有一个点在线段的垂直平分线上,那么这个点到线段的两个端点距离相等.
到线段的两个端点距离相等的点,在线段的垂直平分线上.
逆命题
P
A
B
若PA=PB,则点P在线段AB的垂直平分线上.
已知:PA=PB
求证:点P在线段AB的垂直平分线上.
证明:
过点P作AB的垂线PN,
垂足为C
∵PA=PB,PC⊥AB
∴PC平分AB
∴直线PN是线段AB的垂直平分线
即点P在AB的垂直平分线上
P
A
B
N
C
例题讲解
驶向胜利的彼岸
例1
如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED=
cm;如果∠ECD=600,那么∠EDC=
0.
老师期望:
你能说出填空结果的根据.
E
D
A
B
C
7
60
驶向胜利的彼岸
例2.如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长.
老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去.
B
A
E
D
C
解:∵DE是AB的垂直平分线
∴EA=EB
∵△BCE的周长=EB+EC+BC=50
∴EA+EC+BC=50
即AC+BC=50
∵AC=27
∴BC=23
1.在△ABC中,∠ACB=90°,AB=8cm,BC的垂直平分线DE交AB于D点,则CD=____
4cm
2、在△ABC,PM,QN分别垂直平分AB,AC,则:
(1)若BC=10cm则△APQ的周长=_____cm;
(2)若∠BAC=100°则∠PAQ=______.
10
200
拿出准备好的三角形纸片,用折叠的方法找出每条边的垂直平分线。
思考:刚刚折出来的三条垂直平分线有什么关系?
画—个任意的三角形,并利用直尺和圆规作出三角形三条边的垂直平分线,要注意作图的方法和步骤。
观察作出来的三条垂直平分线有什么特点?对照纸折的三条垂直平分线,是不是它们共有的特点?
三角形三边的垂直平分线交与一点。
结论
如图,△ABC中,边AB、BC的垂直平分线交于点O。
(1)求证:OA=OB=OC。
(2)点O是否也在边AC的垂直平分线上呢?由此你能得出什么结论?
A
P
C
B
证明:∵点O在线段AB的垂直平分线上
∴OA=OB
∵点O在线段BC的垂直平分线上
∴OB=OC
∴OA=OB
∴点O在线段AC的垂直平分线上
3、在△ABC中,AB=AC,AB的中垂线与AC所在的直线相交所得的锐角为50°,则∠B=______.
700或200
例题:
有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。
A
B
C
高
速
公
路
A
B
在某高速公路L的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?你的方案是什么?
生活中的数学
L
课堂小结
本节课学习了哪些知识?
到线段的两端距离相等的点在线段的垂直平分线上.
线段的垂直平分线上的点到线段两个端点的距离相等.
作业
课本第99页习题13.5
第2、3题
