苏科版八年级上册数学 2.6轴对称图形数学活动 折纸与证明 教案
文档属性
| 名称 | 苏科版八年级上册数学 2.6轴对称图形数学活动 折纸与证明 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 201.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-13 00:00:00 | ||
图片预览


文档简介
《折纸与证明》
——与三角形相关的问题
教学目标:
知识技能:通过折纸活动,在操作、交流中,巩固轴对称图形的相关知识;
数学思考:在动手操作过程中,获得数学活动的经验,经历“思考、操作、观察、猜想、验证”等过程,培养推理能力以及分析问题、解决问题的能力;
问题解决:在解决“三角形边与角关系”时,获得分析问题和解决问题的基本方法,并体验解决问题方法的多样性;
在解决“特殊三角形”问题时,获得解决问题的一般方法,体会化归的数学思想.
情感态度:通过活动,感受折纸的魅力,体会生活中处处存在着数学,感受数学的奇妙.
通过生生交流、师生对话,培养有条理的表达能力以及合作交流能力.
教学重点:
经历折纸过程,探究折纸前后图形全等(边、角相等),并利用该性质解决三角形相关的问题,提高学生动手操作能力以及解决问题的能力.
教学难点:
运用所学知识利用折纸得到特殊三角形并证明.
准备材料:
三角形、正方形、长方形、平行四边形纸片若干张
教学思路:
在学生已有的知识、经验基础上,感悟利用折纸可以为证明一些问题提供思路,同时也可以利用折纸折出特殊三角形,为我们解决一些问题提供方法,也是一些折纸创作的基础。教学过程以“发现问题——思考问题——尝试解决问题——交流分享——解决问题”的模式有序进行.
教学过程
一、问题情境
请欣赏一段视频
几张彩色的纸,折出一个多彩世界;几张长纸条,折出了变化多端,这就是折纸的魅力!
我们运用数学知识使折纸更美妙,同时我们也感受着折纸带给数学的思考.
下面我们就一起来尝试用折纸解决与三角形相关的问题,初步感受折纸魅力!
【设计目的】以生动活泼的视频引入,激发学生学习的积极性,活跃课堂氛围,引出主题.
探究活动
探究活动一:三角形
复习回顾
利用折纸的方法找出该三角形的一条高,一条垂直平分线,一条角平分线,并在纸上画出;
【学生活动】操作,并与同伴交流方法.
【教师活动】点评学生的操作,并小结方法.
小结:数学知识:轴对称(翻折);
操作关键:构造相等的边、相等的角.
【设计目的】通过复习回顾,获得折纸活动的数学知识,即轴对称知识,也获得折纸活动的操作关键,即构造相等的边、相等的角;为后续的探究活动奠定基础.
我们在学习等腰三角形的性质里,通过折纸说明了“等边对等角”,那如果这两边不等呢?这两边所对的角有怎样的关系?我们一起尝试探究.
2、拓展探究:三角形中的边角关系
如图,△ABC中,AB>AC. 猜想∠C>∠B.并借助折纸证明.
请折一折,并与同伴交流自己的操作过程与证明思路.
【师生交流,总结】
三种方法:(与复习回顾相呼应):
(1)沿着垂直平分线折叠,构造与∠B相等的∠ECD,利用叠合法比较,∠ECD>∠ACB;
(2)沿着角平分线折叠,构造与∠C相等的∠AC’D,利用三角形外角性质比较,∠AC’D>∠ABC;
(3)沿着高折叠,构造与∠C相等的∠AC’D,利用三角形外角性质比较,∠AC’D>∠ABC.
(1) (2) (3)
操作关键:通过翻折,构造相等的角.
证得结论:在三角形中,“大边对大角”、“小边对小角”
由此,通过折纸可以为我们证明一些命题提供一些思路与方法.
【设计目的】由等腰三角形的性质“等边对等角”,猜测三角形中大边的对角与小边的对角之间的关系,并运用折纸进行证明 .学生通过自主探究、合作交流,获得多种解决问题的方法,并获得解决问题中操作的关键步骤.
(二)探究活动二:特殊三角形
1、等腰三角形
现在给大家一张长方形纸,你能通过折纸、裁剪得到哪些特殊三角形?动手试一试.
等腰三角形(合作交流)
【师生操作、交流】
(1)常用方法(等腰直角三角形)
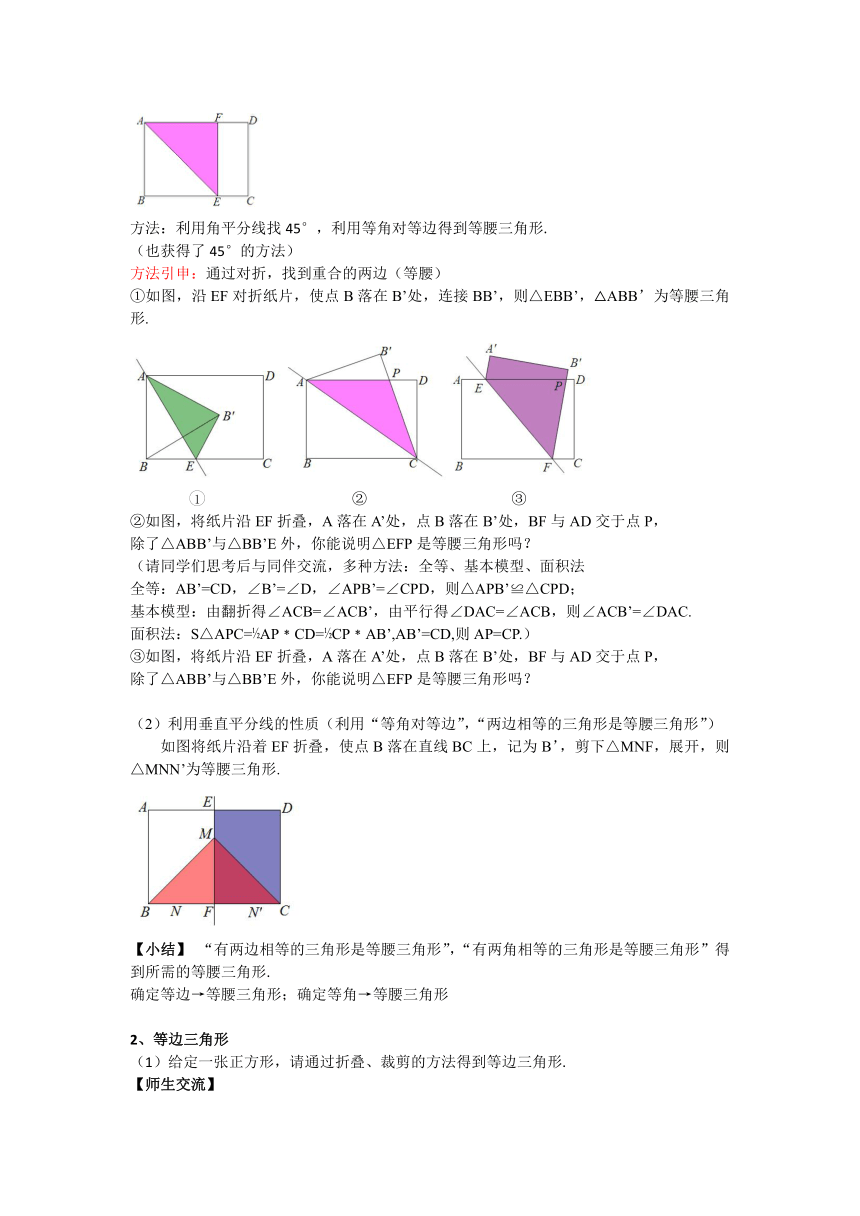
方法:利用角平分线找45°,利用等角对等边得到等腰三角形.
(也获得了45°的方法)
方法引申:通过对折,找到重合的两边(等腰)
①如图,沿EF对折纸片,使点B落在B’处,连接BB’,则△EBB’,△ABB’为等腰三角形.
② ③
②如图,将纸片沿EF折叠,A落在A’处,点B落在B’处,BF与AD交于点P,
除了△ABB’与△BB’E外,你能说明△EFP是等腰三角形吗?
(请同学们思考后与同伴交流,多种方法:全等、基本模型、面积法
全等:AB’=CD,∠B’=∠D,∠APB’=∠CPD,则△APB’≌△CPD;
基本模型:由翻折得∠ACB=∠ACB’,由平行得∠DAC=∠ACB,则∠ACB’=∠DAC.
面积法:S△APC=?AP﹡CD=?CP﹡AB’,AB’=CD,则AP=CP.)
③如图,将纸片沿EF折叠,A落在A’处,点B落在B’处,BF与AD交于点P,
除了△ABB’与△BB’E外,你能说明△EFP是等腰三角形吗?
(2)利用垂直平分线的性质(利用“等角对等边”,“两边相等的三角形是等腰三角形”)
如图将纸片沿着EF折叠,使点B落在直线BC上,记为B’,剪下△MNF,展开,则△MNN’为等腰三角形.
【小结】 “有两边相等的三角形是等腰三角形”,“有两角相等的三角形是等腰三角形”得到所需的等腰三角形.
确定等边→等腰三角形;确定等角→等腰三角形
2、等边三角形
(1)给定一张正方形,请通过折叠、裁剪的方法得到等边三角形.
【师生交流】
利用“三边相等的三角形是等边三角形”
折叠得到垂直平分线,构造等腰三角形,即一组相等的边,现只需得到另一组相等的边即可,因此①CD不折,直接连接CH即可;②将BC翻折,使点C落到H处,连接BH、CH即可。
【小结】方法:①翻折得到垂直平分线,即一组相等的边;②翻折得到另一组相等的边,从而得到等边三角形。
【引申】你能利用正方形纸片折一个60°角吗?
(2)在折叠正方形纸片基础上,思考,如何通过折叠长方形纸片得到等边三角形?说明理由.
【师生交流】
方法1:将长方形转化为正方形问题解决;
方法2:将正方形中折等边三角形的一种方法类比运用于长方形中:
【小结】(1)确定60°→等边三角形;确定相等的边→等边三角形;
(2)获得利用折纸折出60°角的方法;
(3)化归方法.
【设计目的】通过折纸获得特殊三角形,素材由正方形到长方形;特殊三角形由等腰三角形到等边三角形,层层递进,在师生探究、交流中,揭示获得特殊三角形的基本方法,并证明,也体现了化归的数学思想.
三、课堂小结
1、数学知识:折纸问题→轴对称→相等边、角→特殊三角形;
数学方法:化归;
操作关键:构造相等的边与相等的角.
2、若给一张任意纸片,需要折出一个特殊的几何图形,请你说说可以尝试从哪几个思考操作?
【设计目的】由学生总结本节课的数学知识、数学方法、操作关键等,在总结中加强对折纸活动的感受.
四、知识运用
给一张平行四边形纸片,如何通过折叠、裁剪得到一个等边三角形?
【师生交流】
方法1:将平行四边形问题转化为正方形问题解决;
方法2:将正方形中折等边三角形的一种方法类比运用于平行四边形中:
【设计目的】在两个探究活动的基础上,进一步将特殊三角形进行深化,抓住问题的本质,利用垂直平分线构造一组相等的边,利用翻折,构造另一组相等的边,从而获得等边三角形.及时巩固前面所学.
五、结束语
除了平面的几何图形,我们还可以利用折纸折出更多奇妙的图形,你可以再次感受“数学的魅力、折纸的美妙”!
六、课后作业
利用所学知识,通过折纸得到一个作品,与同学分享.
板书设计
折纸与证明——与三角形相关的问题
数学知识:轴对称(翻折);
操作关键:构造相等的边、相等的角.
数学方法:化归
一、三角形中的边角关系
等边对等角
大边对大角、小边对小角
二、等腰三角形 (45°角)
翻折→角平分线→构造相等的角→相等的边
翻折→垂直平分线→构造相等的边
翻折→构造相等的边
三、等边三角形 (60°角、30°角)
垂直平分线(等腰三角形)+一组相等的边(翻折)→等边三角形
∠B=∠ECD, ∠C=∠AC’D ∠C=∠AC’D
∠ECD>∠ACB ∠AC’D>∠B ∠AC’D>∠B
AB=AB’ ∠PAE=∠PEA→PA=PE
BH=HC=BC BH=HC, BH=BC
——与三角形相关的问题
教学目标:
知识技能:通过折纸活动,在操作、交流中,巩固轴对称图形的相关知识;
数学思考:在动手操作过程中,获得数学活动的经验,经历“思考、操作、观察、猜想、验证”等过程,培养推理能力以及分析问题、解决问题的能力;
问题解决:在解决“三角形边与角关系”时,获得分析问题和解决问题的基本方法,并体验解决问题方法的多样性;
在解决“特殊三角形”问题时,获得解决问题的一般方法,体会化归的数学思想.
情感态度:通过活动,感受折纸的魅力,体会生活中处处存在着数学,感受数学的奇妙.
通过生生交流、师生对话,培养有条理的表达能力以及合作交流能力.
教学重点:
经历折纸过程,探究折纸前后图形全等(边、角相等),并利用该性质解决三角形相关的问题,提高学生动手操作能力以及解决问题的能力.
教学难点:
运用所学知识利用折纸得到特殊三角形并证明.
准备材料:
三角形、正方形、长方形、平行四边形纸片若干张
教学思路:
在学生已有的知识、经验基础上,感悟利用折纸可以为证明一些问题提供思路,同时也可以利用折纸折出特殊三角形,为我们解决一些问题提供方法,也是一些折纸创作的基础。教学过程以“发现问题——思考问题——尝试解决问题——交流分享——解决问题”的模式有序进行.
教学过程
一、问题情境
请欣赏一段视频
几张彩色的纸,折出一个多彩世界;几张长纸条,折出了变化多端,这就是折纸的魅力!
我们运用数学知识使折纸更美妙,同时我们也感受着折纸带给数学的思考.
下面我们就一起来尝试用折纸解决与三角形相关的问题,初步感受折纸魅力!
【设计目的】以生动活泼的视频引入,激发学生学习的积极性,活跃课堂氛围,引出主题.
探究活动
探究活动一:三角形
复习回顾
利用折纸的方法找出该三角形的一条高,一条垂直平分线,一条角平分线,并在纸上画出;
【学生活动】操作,并与同伴交流方法.
【教师活动】点评学生的操作,并小结方法.
小结:数学知识:轴对称(翻折);
操作关键:构造相等的边、相等的角.
【设计目的】通过复习回顾,获得折纸活动的数学知识,即轴对称知识,也获得折纸活动的操作关键,即构造相等的边、相等的角;为后续的探究活动奠定基础.
我们在学习等腰三角形的性质里,通过折纸说明了“等边对等角”,那如果这两边不等呢?这两边所对的角有怎样的关系?我们一起尝试探究.
2、拓展探究:三角形中的边角关系
如图,△ABC中,AB>AC. 猜想∠C>∠B.并借助折纸证明.
请折一折,并与同伴交流自己的操作过程与证明思路.
【师生交流,总结】
三种方法:(与复习回顾相呼应):
(1)沿着垂直平分线折叠,构造与∠B相等的∠ECD,利用叠合法比较,∠ECD>∠ACB;
(2)沿着角平分线折叠,构造与∠C相等的∠AC’D,利用三角形外角性质比较,∠AC’D>∠ABC;
(3)沿着高折叠,构造与∠C相等的∠AC’D,利用三角形外角性质比较,∠AC’D>∠ABC.
(1) (2) (3)
操作关键:通过翻折,构造相等的角.
证得结论:在三角形中,“大边对大角”、“小边对小角”
由此,通过折纸可以为我们证明一些命题提供一些思路与方法.
【设计目的】由等腰三角形的性质“等边对等角”,猜测三角形中大边的对角与小边的对角之间的关系,并运用折纸进行证明 .学生通过自主探究、合作交流,获得多种解决问题的方法,并获得解决问题中操作的关键步骤.
(二)探究活动二:特殊三角形
1、等腰三角形
现在给大家一张长方形纸,你能通过折纸、裁剪得到哪些特殊三角形?动手试一试.
等腰三角形(合作交流)
【师生操作、交流】
(1)常用方法(等腰直角三角形)
方法:利用角平分线找45°,利用等角对等边得到等腰三角形.
(也获得了45°的方法)
方法引申:通过对折,找到重合的两边(等腰)
①如图,沿EF对折纸片,使点B落在B’处,连接BB’,则△EBB’,△ABB’为等腰三角形.
② ③
②如图,将纸片沿EF折叠,A落在A’处,点B落在B’处,BF与AD交于点P,
除了△ABB’与△BB’E外,你能说明△EFP是等腰三角形吗?
(请同学们思考后与同伴交流,多种方法:全等、基本模型、面积法
全等:AB’=CD,∠B’=∠D,∠APB’=∠CPD,则△APB’≌△CPD;
基本模型:由翻折得∠ACB=∠ACB’,由平行得∠DAC=∠ACB,则∠ACB’=∠DAC.
面积法:S△APC=?AP﹡CD=?CP﹡AB’,AB’=CD,则AP=CP.)
③如图,将纸片沿EF折叠,A落在A’处,点B落在B’处,BF与AD交于点P,
除了△ABB’与△BB’E外,你能说明△EFP是等腰三角形吗?
(2)利用垂直平分线的性质(利用“等角对等边”,“两边相等的三角形是等腰三角形”)
如图将纸片沿着EF折叠,使点B落在直线BC上,记为B’,剪下△MNF,展开,则△MNN’为等腰三角形.
【小结】 “有两边相等的三角形是等腰三角形”,“有两角相等的三角形是等腰三角形”得到所需的等腰三角形.
确定等边→等腰三角形;确定等角→等腰三角形
2、等边三角形
(1)给定一张正方形,请通过折叠、裁剪的方法得到等边三角形.
【师生交流】
利用“三边相等的三角形是等边三角形”
折叠得到垂直平分线,构造等腰三角形,即一组相等的边,现只需得到另一组相等的边即可,因此①CD不折,直接连接CH即可;②将BC翻折,使点C落到H处,连接BH、CH即可。
【小结】方法:①翻折得到垂直平分线,即一组相等的边;②翻折得到另一组相等的边,从而得到等边三角形。
【引申】你能利用正方形纸片折一个60°角吗?
(2)在折叠正方形纸片基础上,思考,如何通过折叠长方形纸片得到等边三角形?说明理由.
【师生交流】
方法1:将长方形转化为正方形问题解决;
方法2:将正方形中折等边三角形的一种方法类比运用于长方形中:
【小结】(1)确定60°→等边三角形;确定相等的边→等边三角形;
(2)获得利用折纸折出60°角的方法;
(3)化归方法.
【设计目的】通过折纸获得特殊三角形,素材由正方形到长方形;特殊三角形由等腰三角形到等边三角形,层层递进,在师生探究、交流中,揭示获得特殊三角形的基本方法,并证明,也体现了化归的数学思想.
三、课堂小结
1、数学知识:折纸问题→轴对称→相等边、角→特殊三角形;
数学方法:化归;
操作关键:构造相等的边与相等的角.
2、若给一张任意纸片,需要折出一个特殊的几何图形,请你说说可以尝试从哪几个思考操作?
【设计目的】由学生总结本节课的数学知识、数学方法、操作关键等,在总结中加强对折纸活动的感受.
四、知识运用
给一张平行四边形纸片,如何通过折叠、裁剪得到一个等边三角形?
【师生交流】
方法1:将平行四边形问题转化为正方形问题解决;
方法2:将正方形中折等边三角形的一种方法类比运用于平行四边形中:
【设计目的】在两个探究活动的基础上,进一步将特殊三角形进行深化,抓住问题的本质,利用垂直平分线构造一组相等的边,利用翻折,构造另一组相等的边,从而获得等边三角形.及时巩固前面所学.
五、结束语
除了平面的几何图形,我们还可以利用折纸折出更多奇妙的图形,你可以再次感受“数学的魅力、折纸的美妙”!
六、课后作业
利用所学知识,通过折纸得到一个作品,与同学分享.
板书设计
折纸与证明——与三角形相关的问题
数学知识:轴对称(翻折);
操作关键:构造相等的边、相等的角.
数学方法:化归
一、三角形中的边角关系
等边对等角
大边对大角、小边对小角
二、等腰三角形 (45°角)
翻折→角平分线→构造相等的角→相等的边
翻折→垂直平分线→构造相等的边
翻折→构造相等的边
三、等边三角形 (60°角、30°角)
垂直平分线(等腰三角形)+一组相等的边(翻折)→等边三角形
∠B=∠ECD, ∠C=∠AC’D ∠C=∠AC’D
∠ECD>∠ACB ∠AC’D>∠B ∠AC’D>∠B
AB=AB’ ∠PAE=∠PEA→PA=PE
BH=HC=BC BH=HC, BH=BC
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
