幂函数
图片预览





文档简介
(共15张PPT)
幂函数
以上问题中的函数具有什么共同特征
注意:幂函数的解析式必须是 的形式, 其特征可归纳为“两个1:系数为1,只有1项”.
你能说出幂函数与指数函数的区别吗
指数函数:解析式 ,底数为常数
指数为自变量 ;
幂函数:解析式 ,底数为自变量 ,指数为常数 .
判一判
例1:判断下列函数是否为幂函数.
下面研究幂函数
结合图象,研究性质:定义域、值域、单调性、奇偶性、过定点的情况等。
研究
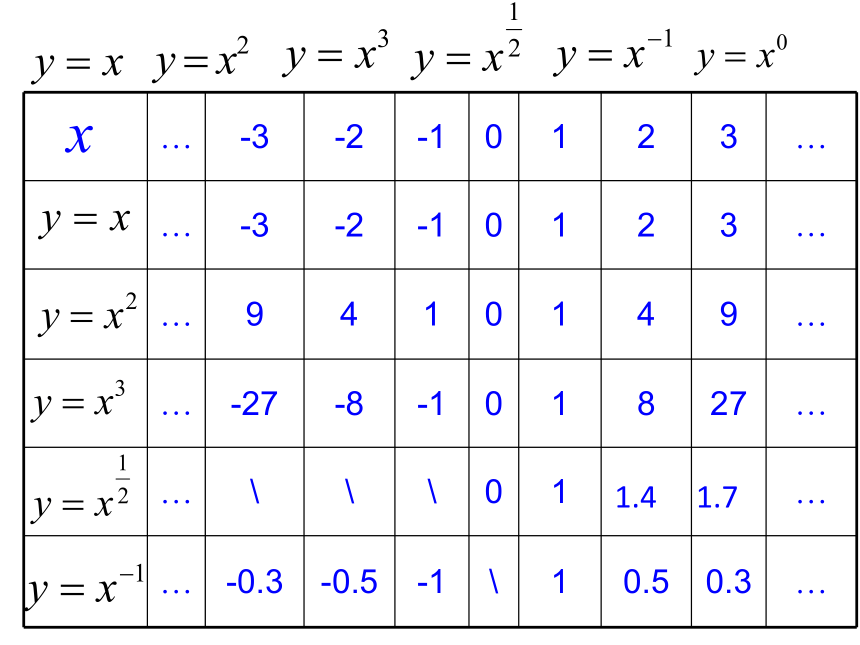
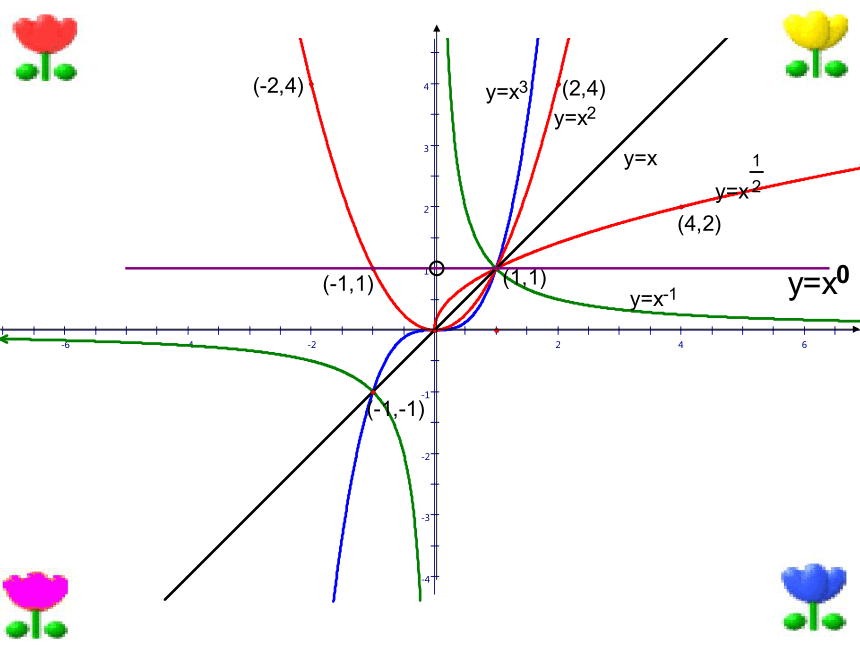
在同一平面直角坐标系内作出这
六个幂函数的图象.
… -3 -2 -1 0 1 2 3 …
… -3 -2 -1 0 1 2 3 …
… 9 4 1 0 1 4 9 …
… -27 -8 -1 0 1 8 27 …
… \ \ \ 0 1 …
… -0.3 -0.5 -1 \ 1 0.5 0.3 …
1.4
1.7
定点?
不管指数是多少,图象都经过哪个定点
图象都经过点(1,1)
时,图象还都过点(0,0)点
定点?
定义域
值域
奇偶性
单调性
公共点
奇
偶
奇
非奇
非偶
奇
(1,1)
R
R
R
{x|x≠0}
[0,+∞)
R
R
{y|y≠0}
[0,+∞)
[0,+∞)
在R上增
在(-∞,0)上减,
观察幂函数图象,将你发现的结论写在下表:
在R上增
在[0,+∞)上增,
在(-∞,0]上减,
在[0,+∞)上增,
在(0,+∞)上减
(1) 所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1);
幂函数的性质
(2) 如果 ,则幂函数图象过原点,并且在区间[0,+∞)上是增函数;
(3) 如果 ,则幂函数图象在区间(0,+∞)上是减函数,在第一象限内,图象向上与 轴无限接近,向右与 轴无限接近;
练习1
1)
2)
3)
<
<
>
证明幂函数 在[0,+∞)上是增函数.
复习用定义证明函数的单调性的步骤:
(4). 下结论.
例2
证明:任取
所以幂函数 在[0,+∞)上是增函数.
(1). 设 是某个区间上任意二值,且 ;
(2). 作差 ,变形 ;
(3). 判断 的符号;
幂函数
定义
五个特殊幂函数
图象
基本性质
本节知识结构:
课堂小结:
P79习题2.3: 1,2,3.
幂函数
以上问题中的函数具有什么共同特征
注意:幂函数的解析式必须是 的形式, 其特征可归纳为“两个1:系数为1,只有1项”.
你能说出幂函数与指数函数的区别吗
指数函数:解析式 ,底数为常数
指数为自变量 ;
幂函数:解析式 ,底数为自变量 ,指数为常数 .
判一判
例1:判断下列函数是否为幂函数.
下面研究幂函数
结合图象,研究性质:定义域、值域、单调性、奇偶性、过定点的情况等。
研究
在同一平面直角坐标系内作出这
六个幂函数的图象.
… -3 -2 -1 0 1 2 3 …
… -3 -2 -1 0 1 2 3 …
… 9 4 1 0 1 4 9 …
… -27 -8 -1 0 1 8 27 …
… \ \ \ 0 1 …
… -0.3 -0.5 -1 \ 1 0.5 0.3 …
1.4
1.7
定点?
不管指数是多少,图象都经过哪个定点
图象都经过点(1,1)
时,图象还都过点(0,0)点
定点?
定义域
值域
奇偶性
单调性
公共点
奇
偶
奇
非奇
非偶
奇
(1,1)
R
R
R
{x|x≠0}
[0,+∞)
R
R
{y|y≠0}
[0,+∞)
[0,+∞)
在R上增
在(-∞,0)上减,
观察幂函数图象,将你发现的结论写在下表:
在R上增
在[0,+∞)上增,
在(-∞,0]上减,
在[0,+∞)上增,
在(0,+∞)上减
(1) 所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1);
幂函数的性质
(2) 如果 ,则幂函数图象过原点,并且在区间[0,+∞)上是增函数;
(3) 如果 ,则幂函数图象在区间(0,+∞)上是减函数,在第一象限内,图象向上与 轴无限接近,向右与 轴无限接近;
练习1
1)
2)
3)
<
<
>
证明幂函数 在[0,+∞)上是增函数.
复习用定义证明函数的单调性的步骤:
(4). 下结论.
例2
证明:任取
所以幂函数 在[0,+∞)上是增函数.
(1). 设 是某个区间上任意二值,且 ;
(2). 作差 ,变形 ;
(3). 判断 的符号;
幂函数
定义
五个特殊幂函数
图象
基本性质
本节知识结构:
课堂小结:
P79习题2.3: 1,2,3.
