《5.3诱导公式(习题)》课件(15张PPT)
文档属性
| 名称 | 《5.3诱导公式(习题)》课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-13 00:00:00 | ||
图片预览




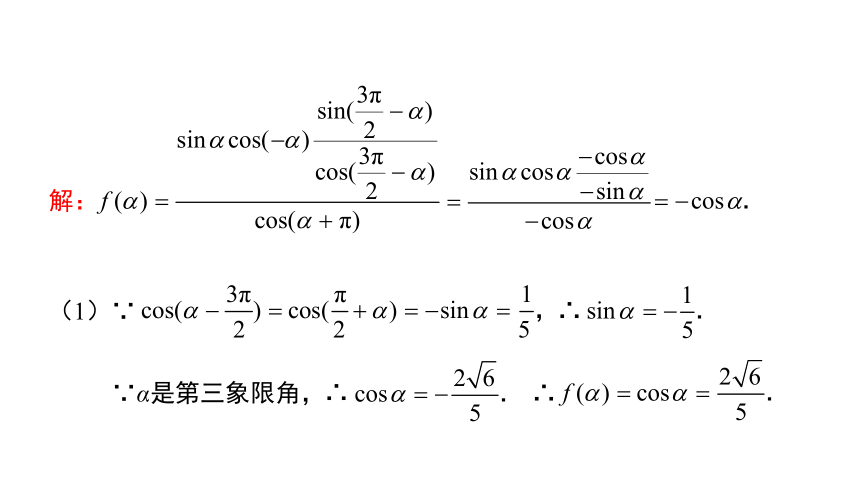
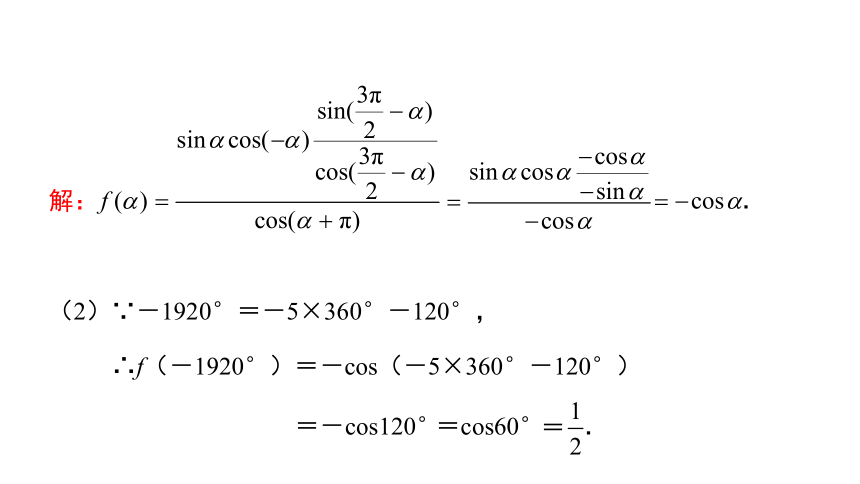

文档简介
5.3 诱导公式
习题
新知探究
例1 已知α是第三象限角,
(1)若 ,求f(α)的值;
(2)若α=-1920°,求f(α)的值.
追问1 根据所给已知条件,首先应该解决什么问题?
由于所给f(α)的表达式很繁琐,因此可先化简再代入求值.
追问2 对于式子中的 与 ,可以直接选用诱导公式,那么,对于 、 、 ,该如何选用公式呢?
新知探究
答:对于 ,因为诱导公式中没有 这种形式,
可以先将拆开为 ,然后分别选用诱导公式二和五消去常数,
当然也可以采用别的途径消去常数,比如,先用诱导公式三,
再用诱导公式一,最后用公式六也可解决;
对于 可以先用公式一,变为 ,
追问2 对于式子中的 与 ,可以直接选用诱导公式,那么,对于 、 、 ,该如何选用公式呢?
新知探究
再用公式四,即可化简,也可以先用公式三,变为 ,
再用公式二,进行化简;
对于 ,可以先用公式一,
变为 ,
再用公式六,即可化简.
新知探究
解:
(1)∵
∴
∵α是第三象限角,
∴
∴
新知探究
解:
(2)∵-1920°=-5×360°-120°,
∴f(-1920°)=-cos(-5×360°-120°)
=-cos120°
=cos60°
=
新知探究
例2 求证:
追问1 根据所给恒等式,应该采用什么样的证明方法?
由于恒等式两边都含有 的形式,因此可以考虑从等式两边分别进行化简.
追问2 你能试着分析一下具体的证明过程吗?
新知探究
左边
选用公式
“1”的代换
消公因式
右边
公式一、二
切化弦,化简
得证
.
新知探究
例2 求证:
证明:
∴左边=右边,故原式得证.
新知探究
例3 已知 求
可以考虑已知角与所求角相加是 的形式,再用诱导公式求解.
追问 已知角与所求角都不是 的形式,怎样利用它们之间的关系求解呢?
新知探究
例3 已知 求
解:∵
∴
∴
∴
∴
归纳小结
问题 通过解决以上的几道题,你觉得在应用诱导公式时需要注意哪些问题?你有什么收获?
(1)适时地运用诱导公式进行转化;
(2)学会分析所给角之间的联系;
(3)根据已知条件会选择恰当的诱导公式进行变形.
作业布置
设 ,求证:
目标检测
已知 ,求 的值.
解:
再见
习题
新知探究
例1 已知α是第三象限角,
(1)若 ,求f(α)的值;
(2)若α=-1920°,求f(α)的值.
追问1 根据所给已知条件,首先应该解决什么问题?
由于所给f(α)的表达式很繁琐,因此可先化简再代入求值.
追问2 对于式子中的 与 ,可以直接选用诱导公式,那么,对于 、 、 ,该如何选用公式呢?
新知探究
答:对于 ,因为诱导公式中没有 这种形式,
可以先将拆开为 ,然后分别选用诱导公式二和五消去常数,
当然也可以采用别的途径消去常数,比如,先用诱导公式三,
再用诱导公式一,最后用公式六也可解决;
对于 可以先用公式一,变为 ,
追问2 对于式子中的 与 ,可以直接选用诱导公式,那么,对于 、 、 ,该如何选用公式呢?
新知探究
再用公式四,即可化简,也可以先用公式三,变为 ,
再用公式二,进行化简;
对于 ,可以先用公式一,
变为 ,
再用公式六,即可化简.
新知探究
解:
(1)∵
∴
∵α是第三象限角,
∴
∴
新知探究
解:
(2)∵-1920°=-5×360°-120°,
∴f(-1920°)=-cos(-5×360°-120°)
=-cos120°
=cos60°
=
新知探究
例2 求证:
追问1 根据所给恒等式,应该采用什么样的证明方法?
由于恒等式两边都含有 的形式,因此可以考虑从等式两边分别进行化简.
追问2 你能试着分析一下具体的证明过程吗?
新知探究
左边
选用公式
“1”的代换
消公因式
右边
公式一、二
切化弦,化简
得证
.
新知探究
例2 求证:
证明:
∴左边=右边,故原式得证.
新知探究
例3 已知 求
可以考虑已知角与所求角相加是 的形式,再用诱导公式求解.
追问 已知角与所求角都不是 的形式,怎样利用它们之间的关系求解呢?
新知探究
例3 已知 求
解:∵
∴
∴
∴
∴
归纳小结
问题 通过解决以上的几道题,你觉得在应用诱导公式时需要注意哪些问题?你有什么收获?
(1)适时地运用诱导公式进行转化;
(2)学会分析所给角之间的联系;
(3)根据已知条件会选择恰当的诱导公式进行变形.
作业布置
设 ,求证:
目标检测
已知 ,求 的值.
解:
再见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
