青岛版九年级上1.5梯形第一课时

1.5梯形
第一课时 等腰梯形的性质
山东省单县终兴中学 编写人 王敏 吴吉杰
一 学习目标
1记住梯形、等腰梯形、直角梯形的定义
2掌握等腰梯形的性质，并能灵活的应用
二 自主预习
（一）梯形
1.一组对边 而另一组对边 的四边形叫做梯形。 的两边叫做梯形的底， 的两边叫做梯形的腰。夹在两底之间与底 的线段叫做梯形的高。
2. 的梯形叫做等腰梯形， 的梯形叫做直角梯形。
（二）等腰梯形的性质
1.等腰梯形同一底上得两个内角 。
2.等腰梯形的两条对角线 。
3.等腰梯形是 图形。
三 导学探究
（一）梯形的初步认识
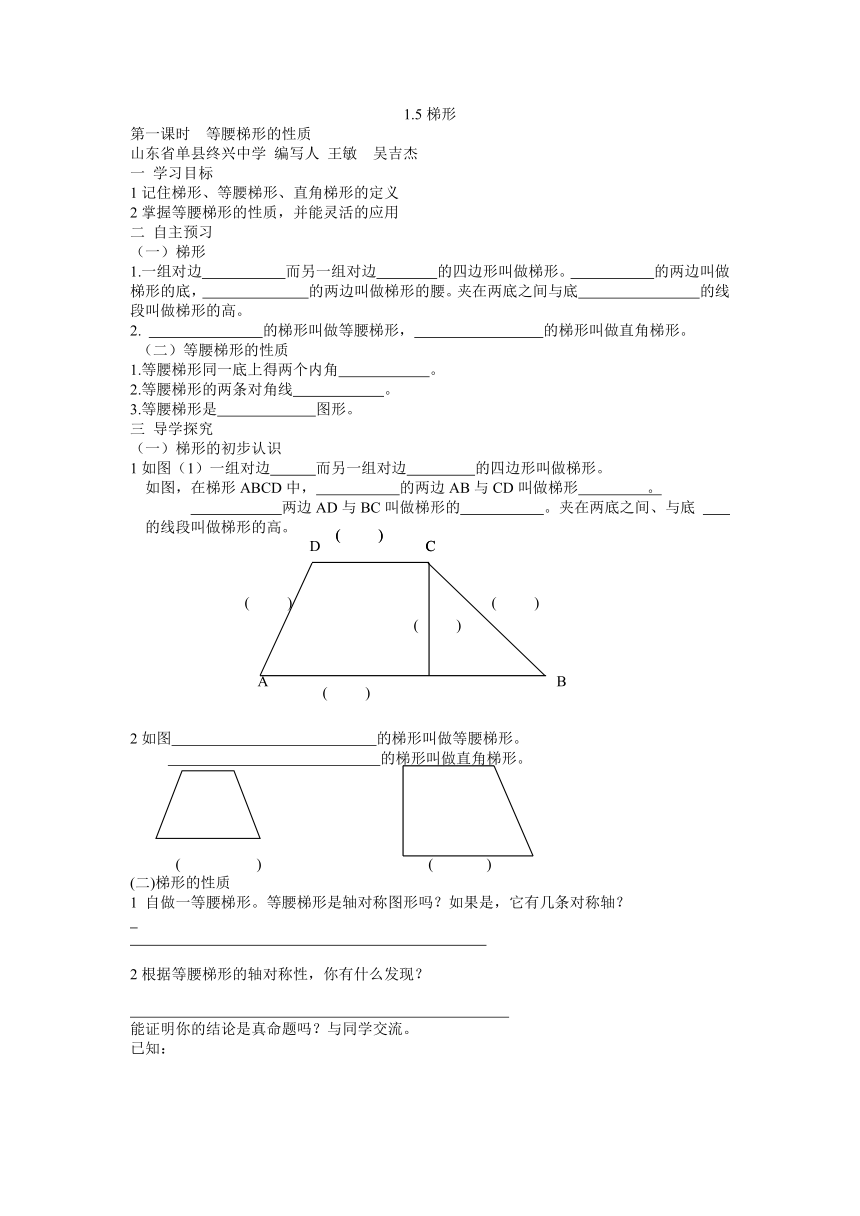
1如图（1）一组对边 而另一组对边 的四边形叫做梯形。
如图，在梯形ABCD中， 的两边AB与CD叫做梯形 。
两边AD与BC叫做梯形的 。夹在两底之间、与底
的线段叫做梯形的高。
2如图 的梯形叫做等腰梯形。
的梯形叫做直角梯形。
( ) ( )
(二)梯形的性质
1 自做一等腰梯形。等腰梯形是轴对称图形吗？如果是，它有几条对称轴？
2根据等腰梯形的轴对称性，你有什么发现？
能证明你的结论是真命题吗？与同学交流。
已知：
求证：
证明：
结论：
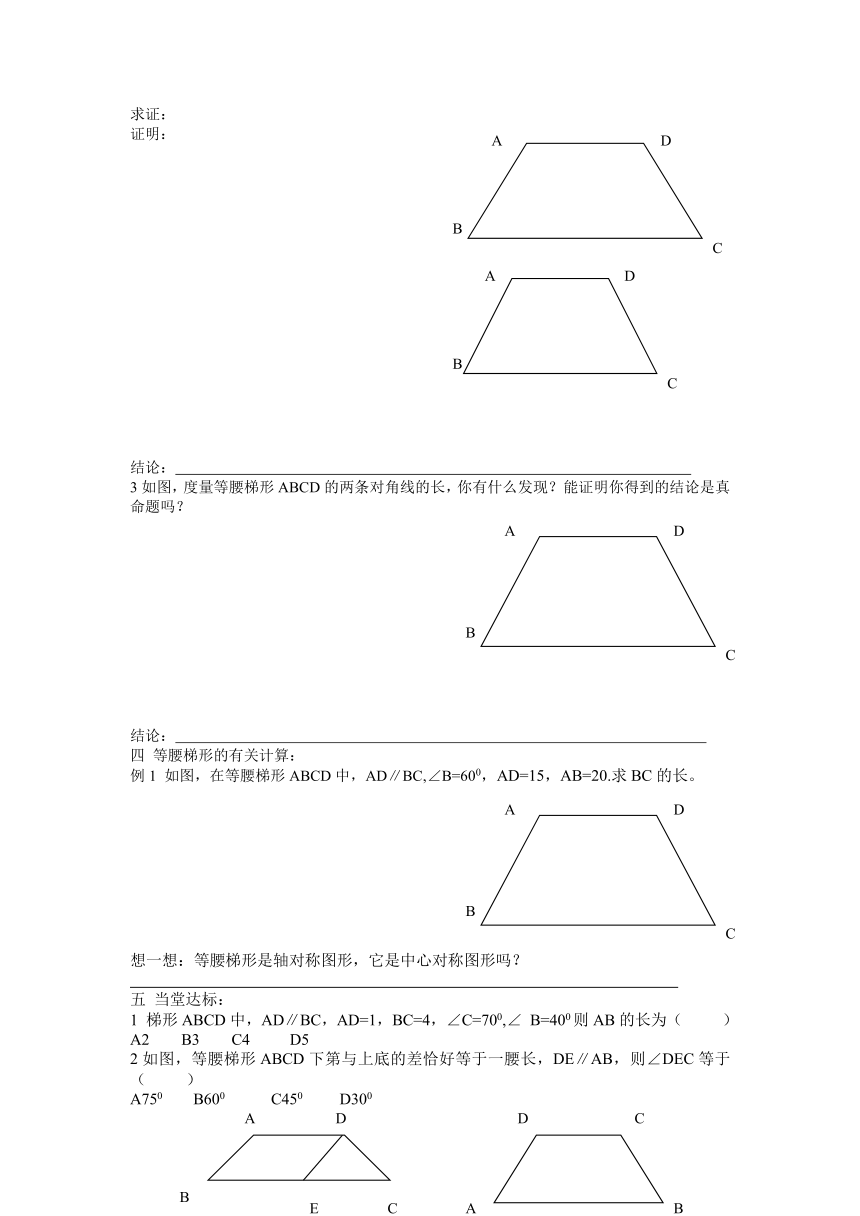
3如图，度量等腰梯形ABCD的两条对角线的长，你有什么发现？能证明你得到的结论是真命题吗？
结论：
四 等腰梯形的有关计算：
例1 如图，在等腰梯形ABCD中，AD∥BC,∠B=600，AD=15，AB=20.求BC的长。
想一想：等腰梯形是轴对称图形，它是中心对称图形吗？
五 当堂达标：
1 梯形ABCD中，AD∥BC，AD=1，BC=4，∠C=700,∠ B=400则AB的长为（ ）
A2 B3 C4 D5
2如图，等腰梯形ABCD下第与上底的差恰好等于一腰长，DE∥AB，则∠DEC等于（ ）
A750 B600 C450 D300
3如图，等腰梯形ABCD中，AB∥DC,AD=BC=8，AB=10， CD=6，则梯形ABCD的面积是（ ）
A16 B16 C32 D16
4 如图，在等腰梯形ABCD中，AD∥BC,对角线AC⊥BD于点O，AE⊥BC,DF⊥BC,垂足分别为E,F设AD=a,BC=b,则四边形AEFD的周长是（ ）
A3a+b B2( a+b) C2b+a D4a+b
5 如图，梯形ABCD的两条对角线交于点E,图中面积相等的三角形有 对
6在等腰梯形ABCD中，AD∥BC，AD=3cm,AB=4cm,B=600则下底BC的长为 cm
7在等腰梯形ABCD中，AD∥BC,AD=1，AB=CD=2，BC=3，则∠B=
8如图，在梯形ABCD中AB∥CD,BD⊥AD,BC=CD,A=600,CD=2cm.
( 1)求∠CBD得度数
（2）求下底AB的长
9如图，梯形ABCD中，AD∥BC，DC⊥BC，将梯形沿对角线BD折叠，点A恰好落在DC上得A′处，若∠A′BC＝200，则∠A′BD的度数是（ ）
A 150 B 200 C 250 D 300
10有一个直角梯形ABCD零件，AD∥BC，斜腰DC的长
为10cm，∠D＝1200，则该零件另一腰AB的长为
11如图等腰梯形ABCD中，AB∥DC，
AC⊥BC，点E是AB的中点，EC∥AD，
∠ABC＝ （ ）
A 750 B 700 C 600 D 300 （9题图）
12如图等腰梯形ABCD中AD∥BC，∠B＝600
AD＝4，BC＝7，则梯形ABCD的周长是 (10题图)
（ (12题图)
（
（11题图）
13如图在梯形ABCD中，AD∥BC，AB＝DA＝DC，
AC⊥AB，将CB延长至点F，使BF＝CD，
（1）求∠ABC的度数；（2）求证：
△CAF为等腰三角形
14如图在梯形ABCD的两条对角线交于点E，图中面积相等的三角形共有
A
B
C
D
( )
( )
( )
( )
( )
C
( )
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
D
C
A
B
D
C
E
A′
D
C
B
A
D
C
B
A
D
C
B
A
E
D
C
B
A
E
D
C
B
A