特殊的平行四边形导学案
图片预览
文档简介
知识改变命运 学习创造未来 成功=50%的学习策略+40%的努力程度+10%的智商
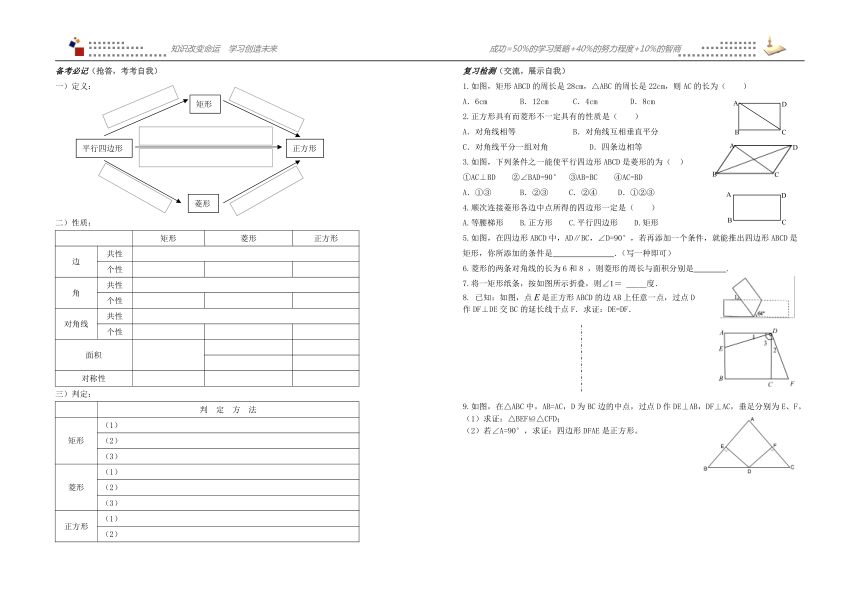
备考必记(抢答,考考自我)
一)定义:
二)性质:
矩形 菱形 正方形
边 共性
个性
角 共性
个性
对角线 共性
个性
面积
对称性
三)判定:
判 定 方 法
矩形 (1)
(2)
(3)
菱形 (1)
(2)
(3)
正方形 (1)
(2)
复习检测(交流,展示自我)
1.如图,矩形ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A.6cm B.12cm C.4cm D.8cm
2.正方形具有而菱形不一定具有的性质是( )
A.对角线相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.四条边相等
3.如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD ②∠BAD=90° ③AB=BC ④AC=BD
A.①③ B.②③ C.②④ D.①②③
4.顺次连接菱形各边中点所得的四边形一定是( )
A.等腰梯形 B.正方形 C.平行四边形 D.矩形
5.如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是
矩形,你所添加的条件是 .(写一种即可)
6.菱形的两条对角线的长为6和8 ,则菱形的周长与面积分别是 .
7.将一矩形纸条,按如图所示折叠,则∠1= _____度.
8. 已知:如图,点是正方形ABCD的边AB上任意一点,过点D
作DF⊥DE交BC的延长线于点F.求证:DE=DF.
9.如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F。
(1)求证:△BEF≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形。
合作探究(超越自我)
10.如图,分别以△ABC的三边为边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF。
请回答下列问题:
(1)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?
(2)说明四边形ADEF是什么特殊四边形?
(3)当△ABC满足什么条件时,四边形ADEF是矩形?
(4)当△ABC满足什么条件时,四边形ADEF是菱形?
(5)当△ABC满足什么条件时,四边形ADEF是正方形?
反思小结(完善自我)
谈谈你对本堂课的收获与体会。
达标检测(检阅自我)
11.如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是 _______。
12.在矩形ABCD中,对角线AC,BD相交于点O,若∠AOB=60°,AB=4cm,则AC的长为
________cm.
13.如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为 .
14.(提高题)如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN
交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
课外练习(巩固自我)
《娄底市初中毕业学业考试指南》P90-91/1,2,3,4,5,6,8
Te shu ping xing si bian xing dao xue an
■设计与编导 桥头河镇株木中学谢彦文
矩形
正方形
平行四边形
菱形
D
C
B
A
D
C
B
A
D
A
B
C
B
A
C
D
E
F
11题图
专题复习
◆ 知识目标:掌握特殊平行四边形的定义及相关性质和判定方法。
◆ 能力目标:培养概括归纳能力、逻辑推理能力和创新能力。
◆ 情感与态度:在学习活动中发展主动探索和独立思考的习惯,获得成功的体验。
◆ 重点:特殊平行四边形的性质与判定的应用。
◆ 难点:发展合情推理和初步的演绎推理能力。
复
习
目
标
13题图
备考必记(抢答,考考自我)
一)定义:
二)性质:
矩形 菱形 正方形
边 共性
个性
角 共性
个性
对角线 共性
个性
面积
对称性
三)判定:
判 定 方 法
矩形 (1)
(2)
(3)
菱形 (1)
(2)
(3)
正方形 (1)
(2)
复习检测(交流,展示自我)
1.如图,矩形ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A.6cm B.12cm C.4cm D.8cm
2.正方形具有而菱形不一定具有的性质是( )
A.对角线相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.四条边相等
3.如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD ②∠BAD=90° ③AB=BC ④AC=BD
A.①③ B.②③ C.②④ D.①②③
4.顺次连接菱形各边中点所得的四边形一定是( )
A.等腰梯形 B.正方形 C.平行四边形 D.矩形
5.如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD是
矩形,你所添加的条件是 .(写一种即可)
6.菱形的两条对角线的长为6和8 ,则菱形的周长与面积分别是 .
7.将一矩形纸条,按如图所示折叠,则∠1= _____度.
8. 已知:如图,点是正方形ABCD的边AB上任意一点,过点D
作DF⊥DE交BC的延长线于点F.求证:DE=DF.
9.如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F。
(1)求证:△BEF≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形。
合作探究(超越自我)
10.如图,分别以△ABC的三边为边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF。
请回答下列问题:
(1)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?
(2)说明四边形ADEF是什么特殊四边形?
(3)当△ABC满足什么条件时,四边形ADEF是矩形?
(4)当△ABC满足什么条件时,四边形ADEF是菱形?
(5)当△ABC满足什么条件时,四边形ADEF是正方形?
反思小结(完善自我)
谈谈你对本堂课的收获与体会。
达标检测(检阅自我)
11.如图,四边形ABCD是正方形,延长AB到E,使AE=AC,则∠BCE的度数是 _______。
12.在矩形ABCD中,对角线AC,BD相交于点O,若∠AOB=60°,AB=4cm,则AC的长为
________cm.
13.如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为 .
14.(提高题)如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN
交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
课外练习(巩固自我)
《娄底市初中毕业学业考试指南》P90-91/1,2,3,4,5,6,8
Te shu ping xing si bian xing dao xue an
■设计与编导 桥头河镇株木中学谢彦文
矩形
正方形
平行四边形
菱形
D
C
B
A
D
C
B
A
D
A
B
C
B
A
C
D
E
F
11题图
专题复习
◆ 知识目标:掌握特殊平行四边形的定义及相关性质和判定方法。
◆ 能力目标:培养概括归纳能力、逻辑推理能力和创新能力。
◆ 情感与态度:在学习活动中发展主动探索和独立思考的习惯,获得成功的体验。
◆ 重点:特殊平行四边形的性质与判定的应用。
◆ 难点:发展合情推理和初步的演绎推理能力。
复
习
目
标
13题图
