梯形
图片预览
文档简介
16.3梯形的性质
【学习目标】
了解梯形,等腰梯形,直角梯形的概念,探索并理解记忆等腰梯形的有关性质。
能够应用梯形的有关性质进行有关问题的论证和计算,培养学生的分析能力和计算能力。
3.通过添加辅助线,把梯形的问题转化为平行四边形和三角形问题,使学生体会图形变换的方法和转化的思想。
【教学过程】
1.小学我们已经学过梯形,你能说说生活中见过那些梯形的物体或图形吗?
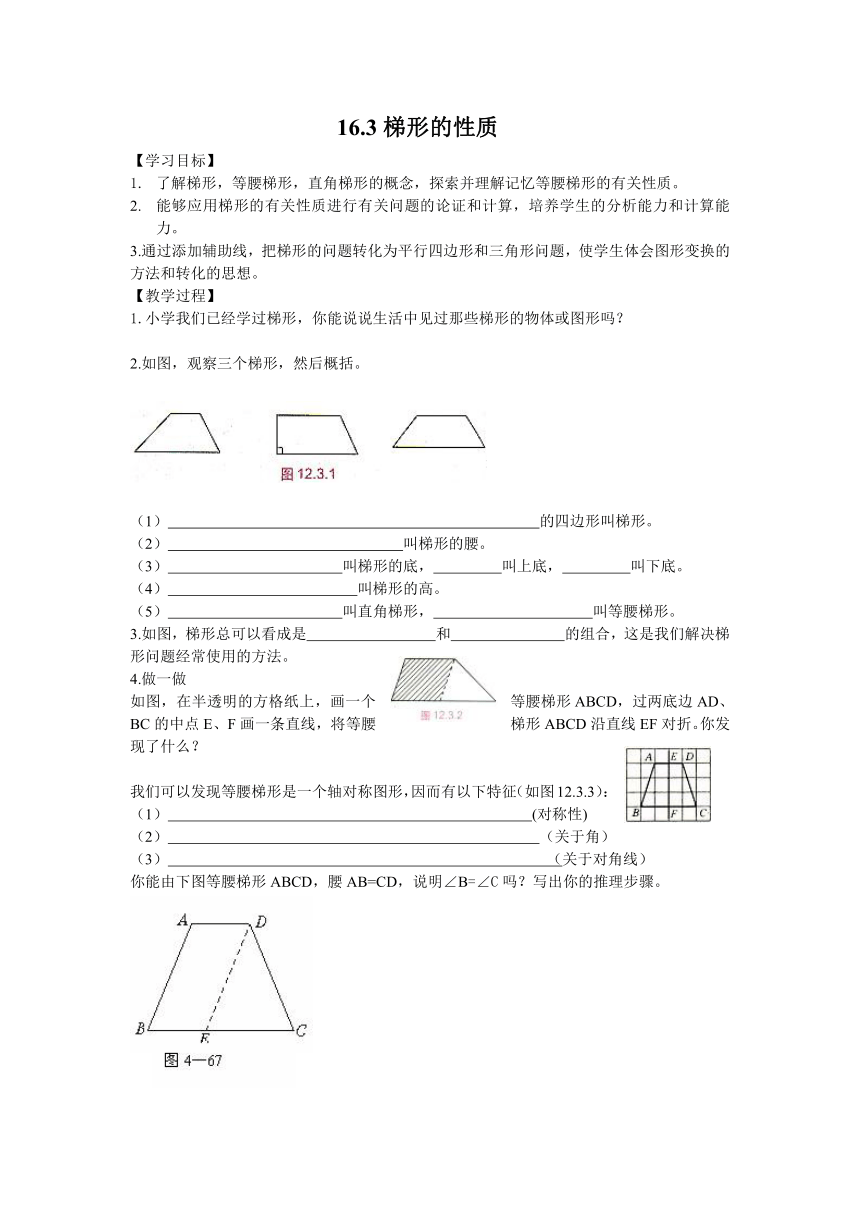
2.如图,观察三个梯形,然后概括。
(1) 的四边形叫梯形。
(2) 叫梯形的腰。
(3) 叫梯形的底, 叫上底, 叫下底。
(4) 叫梯形的高。
(5) 叫直角梯形, 叫等腰梯形。
3.如图,梯形总可以看成是 和 的组合,这是我们解决梯形问题经常使用的方法。
4.做一做
如图,在半透明的方格纸上,画一个等腰梯形ABCD,过两底边AD、BC的中点E、F画一条直线,将等腰梯形ABCD沿直线EF对折。你发现了什么?
我们可以发现等腰梯形是一个轴对称图形,因而有以下特征(如图12.3.3):
(1) (对称性)
(2) (关于角)
(3) (关于对角线)
你能由下图等腰梯形ABCD,腰AB=CD,说明∠B=∠C吗?写出你的推理步骤。
【应用举例】
例1如图12.3.4,延长等腰梯形ABCD的两腰BA与CD,相交于点E。试说明△
EBC和△EAD都是等腰三角形。
例2如图12.3.5,在等腰梯形ABCD中,AB∥DC,CE∥DA。
已知AB=8,DC=5,DA=6,求△CEB的周长。
练习,完成P111练习1、2题。
【综合应用】
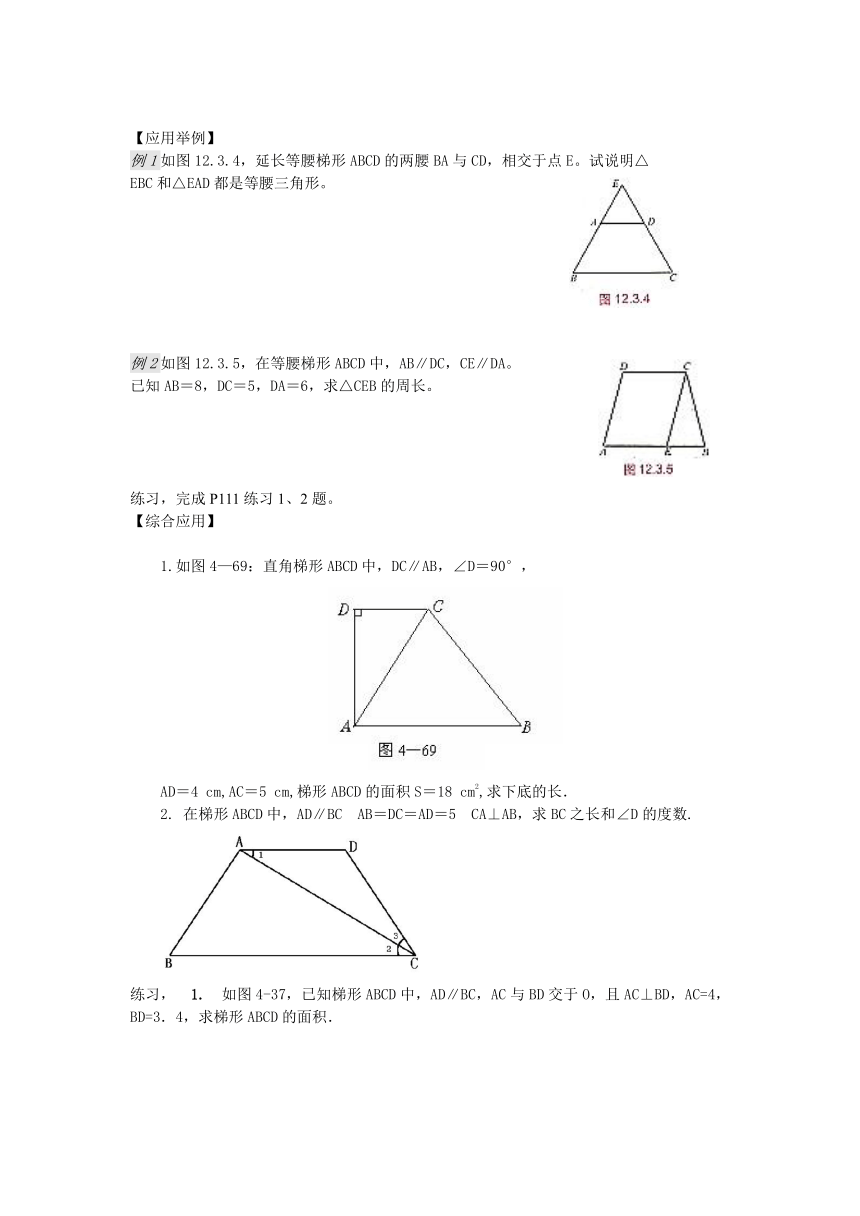
1.如图4—69:直角梯形ABCD中,DC∥AB,∠D=90°,
AD=4 cm,AC=5 cm,梯形ABCD的面积S=18 cm2,求下底的长.
2. 在梯形ABCD中,AD∥BC AB=DC=AD=5 CA⊥AB,求BC之长和∠D的度数.
练习, 1. 如图4-37,已知梯形ABCD中,AD∥BC,AC与BD交于O,且AC⊥BD,AC=4,BD=3.4,求梯形ABCD的面积.
2. 如图12-3-3,在梯形ABCD中,AD∥BC,AD=AB=DC,BD⊥CD.求∠C的大小.
【拓展提高】
1.解决梯形问题的基本思路:
.
这种思路常通过平移或旋转来实现.
2. 梯形的面积(如图12-3-1):
.
3.梯形中常见的辅助线
【拓展应用】
1. 在等腰梯形ABCD中AD∥CB,AD=3,AB=5,BC=8,求∠B的度.
2. 如图,已知:等腰梯形ABCD中,AD∥BC,AC⊥BD,AD+BC=16,求梯形的高.
3. 如图12-3-8,等腰梯形ABCD中,AD∥BC,AB=CD,对角线AC⊥BD,AD=4cm,BC=10cm.求梯形的面积.
4. 已知,如图;在梯形ABCD中,AD∥BC,AD<BC,E,F分别为AD,BC的中点,且EF⊥BC,求证:∠B=∠C.
练习:1. 1.如图4.9-14,在等腰梯形ABCD中,对角线AC与BD互相垂直,且AD=3cm,BC=7cm,求BD的长度.
2. 已知,在梯形ABCD中,AD∥BC,AB=AC,∠BAC=90°,BD=BC,BD交AC于O,求证:CD=CD.
3.如图12-3-12,在梯形ABCD中,AD∥BC,∠B=40°,∠C=70°,试说明AB+AD=BC.
【学习目标】
了解梯形,等腰梯形,直角梯形的概念,探索并理解记忆等腰梯形的有关性质。
能够应用梯形的有关性质进行有关问题的论证和计算,培养学生的分析能力和计算能力。
3.通过添加辅助线,把梯形的问题转化为平行四边形和三角形问题,使学生体会图形变换的方法和转化的思想。
【教学过程】
1.小学我们已经学过梯形,你能说说生活中见过那些梯形的物体或图形吗?
2.如图,观察三个梯形,然后概括。
(1) 的四边形叫梯形。
(2) 叫梯形的腰。
(3) 叫梯形的底, 叫上底, 叫下底。
(4) 叫梯形的高。
(5) 叫直角梯形, 叫等腰梯形。
3.如图,梯形总可以看成是 和 的组合,这是我们解决梯形问题经常使用的方法。
4.做一做
如图,在半透明的方格纸上,画一个等腰梯形ABCD,过两底边AD、BC的中点E、F画一条直线,将等腰梯形ABCD沿直线EF对折。你发现了什么?
我们可以发现等腰梯形是一个轴对称图形,因而有以下特征(如图12.3.3):
(1) (对称性)
(2) (关于角)
(3) (关于对角线)
你能由下图等腰梯形ABCD,腰AB=CD,说明∠B=∠C吗?写出你的推理步骤。
【应用举例】
例1如图12.3.4,延长等腰梯形ABCD的两腰BA与CD,相交于点E。试说明△
EBC和△EAD都是等腰三角形。
例2如图12.3.5,在等腰梯形ABCD中,AB∥DC,CE∥DA。
已知AB=8,DC=5,DA=6,求△CEB的周长。
练习,完成P111练习1、2题。
【综合应用】
1.如图4—69:直角梯形ABCD中,DC∥AB,∠D=90°,
AD=4 cm,AC=5 cm,梯形ABCD的面积S=18 cm2,求下底的长.
2. 在梯形ABCD中,AD∥BC AB=DC=AD=5 CA⊥AB,求BC之长和∠D的度数.
练习, 1. 如图4-37,已知梯形ABCD中,AD∥BC,AC与BD交于O,且AC⊥BD,AC=4,BD=3.4,求梯形ABCD的面积.
2. 如图12-3-3,在梯形ABCD中,AD∥BC,AD=AB=DC,BD⊥CD.求∠C的大小.
【拓展提高】
1.解决梯形问题的基本思路:
.
这种思路常通过平移或旋转来实现.
2. 梯形的面积(如图12-3-1):
.
3.梯形中常见的辅助线
【拓展应用】
1. 在等腰梯形ABCD中AD∥CB,AD=3,AB=5,BC=8,求∠B的度.
2. 如图,已知:等腰梯形ABCD中,AD∥BC,AC⊥BD,AD+BC=16,求梯形的高.
3. 如图12-3-8,等腰梯形ABCD中,AD∥BC,AB=CD,对角线AC⊥BD,AD=4cm,BC=10cm.求梯形的面积.
4. 已知,如图;在梯形ABCD中,AD∥BC,AD<BC,E,F分别为AD,BC的中点,且EF⊥BC,求证:∠B=∠C.
练习:1. 1.如图4.9-14,在等腰梯形ABCD中,对角线AC与BD互相垂直,且AD=3cm,BC=7cm,求BD的长度.
2. 已知,在梯形ABCD中,AD∥BC,AB=AC,∠BAC=90°,BD=BC,BD交AC于O,求证:CD=CD.
3.如图12-3-12,在梯形ABCD中,AD∥BC,∠B=40°,∠C=70°,试说明AB+AD=BC.
