直线与圆的位置关系
图片预览




文档简介
(共15张PPT)
山水相搂的地方出现了一道红霞,过了一会儿,那里出现了太阳的小半边脸,慢慢儿,一纵一纵地使劲儿向上升,到了最后,它终于冲破了云霞,完全跳出了海面。
——巴 金
到了最后,它终于冲破了云霞,完全跳出了海面。
山水相搂的地方出现了一道红霞,
过了一会儿,那里出现了太阳的小半边脸,
慢慢儿,一纵一纵地使劲儿向上升,
观察与思考
直线与圆的位置关系除了这三种外,还有别的可能吗?它们各有何特点?
图1
图2
图3
设计与制作:株木中学谢彦文
l1
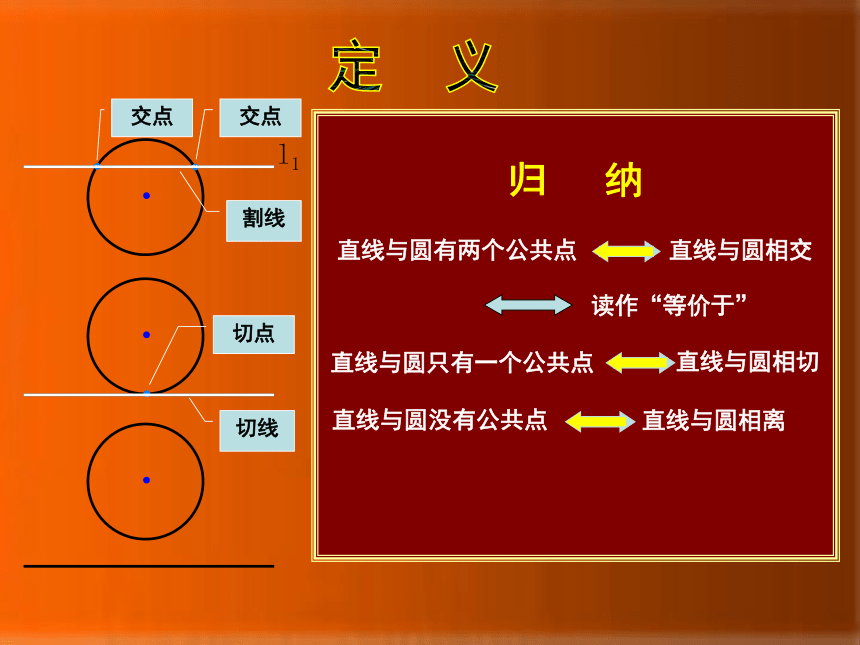
直线和圆有两个公共点时,叫做直线和圆相交;
直线和圆有唯一公共点时,叫做直线和圆相切;
直线和圆没有公共点时,叫做直线和圆相离.
交点
交点
这时直线叫做圆的割线.
这时直线叫做圆的切线.
唯一的公共点叫做切点.
割线
切点
切线
归 纳
直线与圆有两个公共点
直线与圆相交
读作“等价于”
直线与圆只有一个公共点
直线与圆相切
直线与圆没有公共点
直线与圆相离
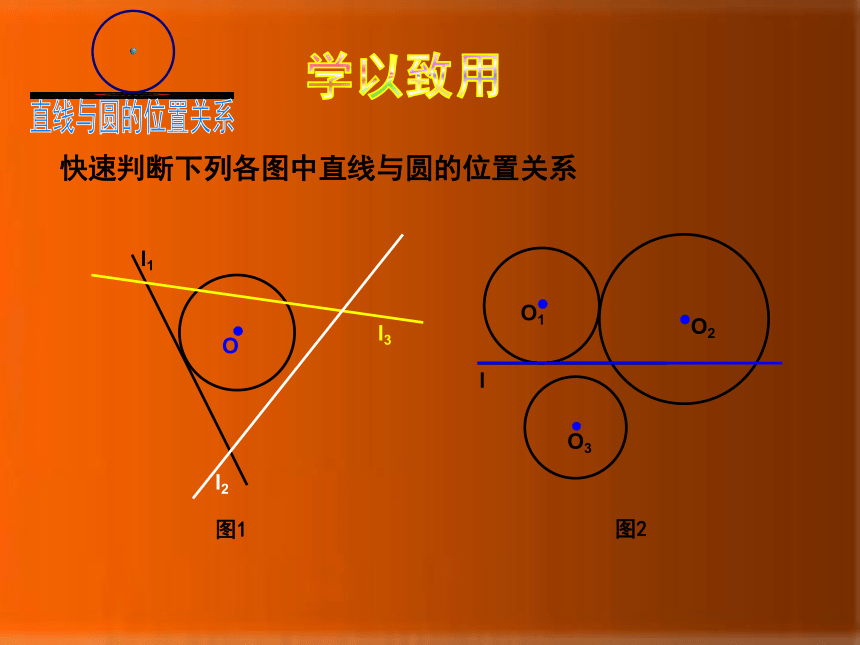
快速判断下列各图中直线与圆的位置关系
l3
l2
l1
O
图1
图2
O3
O2
O1
l
●
●
●
●
C
B
A
O
O
∟
A
d
r
A
B
r
r
r
∟
A
相 离
相 切
相 交
直线L和⊙O相交
d直线L和⊙O相切
d=r
直线L和⊙O相离
d>r
l
O
l
l
B
∟
1)直线与圆最多有两个公共点。
2)若A是⊙O上一点,则直线AB与⊙O相切。
3)若C为⊙O外一点,则过点C的直线CD与⊙O 相交或相离。
一、判断
二、填空
三、选择
1)设⊙O的半径为4,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=4
已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
2)设⊙p的半径为4cm,直线l上一点A到圆心的距离4cm,则直线l与⊙O的位置关系是…………( )
A、相交 B、相切 C、相离 D、相切或相交
√
×
×
相离
相交
相切
2
1
0
C
D
1.已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。
相离
相切
O
X
Y
.
A
3
C
∟
4
B
∟
2.在Rt△ABC,∠C=900,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB所在的直线有怎样的位置关系 为什么
(1)r=2 cm ; (2)r=2.4 cm ; (3) r=3 cm.
5
2.4
4
3
B
C
A
∟
D
∟
2
2
(1)当r=2cm时, ∵d>r,∴⊙C与AB相离。
即圆心C到AB的距离d=2.4cm。
(2)当r=2.4cm时, ∵d=r, ∴⊙C与AB相切。
(3)当r=3cm时, ∵d<r,∴⊙C与AB相交。
根据三角形面积公式有 CD·AB=AC·BC
=5(cm)
2
2
AB=
解:在Rt△ABC中,
2
2
=
= 2.4(cm)。
∴CD=
=
3.在Rt△ABC,∠C=900,AC=3cm,BC=4cm,以C为圆心,r满足怎样的条件时,C圆与线段AB只有一个交点
2.4
4
3
B
C
A
∟
D
∟
说说收获
直线与圆的位置关系
相 交 相 切 相 离
图 形
公共点个数
公共点名称
直线名称
d与r的关系
d
r
O
l
2 个
交点
割线
1 个
切点
切线
d < r
d = r
d > r
没有
∟
d
r
∟
d
r
判定直线与圆的位置关系的方法有2种:
(1)根据定义,由_____________________的个数来判断;
(2)根据性质,由___________________________的关系来判断。
直线与圆的公共点
圆心到直线的距离d与半径r
在实际应用中,常采用第(2)种方法来判定。
相离
没有公共点
d﹥r
相切
只有一个公共点
d = r
相交
有两个公共点
d < r
2.(必做题)如图:已知∠ AOB=30°,M为OB上一点,且OM=5cm,以M为圆心,以r为半径的圆与直线OA有怎样的位置关系?为什么?
(1)r=2cm; (2)r=4cm; (3)r=2.5cm.
●
O
M
B
A
课堂练习
1.(必做题)P73/练习/1.2.
在第2题中,当r满足什么条件时, ⊙M与射线OA只有一个交点?
拓展训练(选做题)
山水相搂的地方出现了一道红霞,过了一会儿,那里出现了太阳的小半边脸,慢慢儿,一纵一纵地使劲儿向上升,到了最后,它终于冲破了云霞,完全跳出了海面。
——巴 金
到了最后,它终于冲破了云霞,完全跳出了海面。
山水相搂的地方出现了一道红霞,
过了一会儿,那里出现了太阳的小半边脸,
慢慢儿,一纵一纵地使劲儿向上升,
观察与思考
直线与圆的位置关系除了这三种外,还有别的可能吗?它们各有何特点?
图1
图2
图3
设计与制作:株木中学谢彦文
l1
直线和圆有两个公共点时,叫做直线和圆相交;
直线和圆有唯一公共点时,叫做直线和圆相切;
直线和圆没有公共点时,叫做直线和圆相离.
交点
交点
这时直线叫做圆的割线.
这时直线叫做圆的切线.
唯一的公共点叫做切点.
割线
切点
切线
归 纳
直线与圆有两个公共点
直线与圆相交
读作“等价于”
直线与圆只有一个公共点
直线与圆相切
直线与圆没有公共点
直线与圆相离
快速判断下列各图中直线与圆的位置关系
l3
l2
l1
O
图1
图2
O3
O2
O1
l
●
●
●
●
C
B
A
O
O
∟
A
d
r
A
B
r
r
r
∟
A
相 离
相 切
相 交
直线L和⊙O相交
d
d=r
直线L和⊙O相离
d>r
l
O
l
l
B
∟
1)直线与圆最多有两个公共点。
2)若A是⊙O上一点,则直线AB与⊙O相切。
3)若C为⊙O外一点,则过点C的直线CD与⊙O 相交或相离。
一、判断
二、填空
三、选择
1)设⊙O的半径为4,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d为…( )
A、d≤4 B、d<4 C、d≥4 D、d=4
已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
2)设⊙p的半径为4cm,直线l上一点A到圆心的距离4cm,则直线l与⊙O的位置关系是…………( )
A、相交 B、相切 C、相离 D、相切或相交
√
×
×
相离
相交
相切
2
1
0
C
D
1.已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。
相离
相切
O
X
Y
.
A
3
C
∟
4
B
∟
2.在Rt△ABC,∠C=900,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB所在的直线有怎样的位置关系 为什么
(1)r=2 cm ; (2)r=2.4 cm ; (3) r=3 cm.
5
2.4
4
3
B
C
A
∟
D
∟
2
2
(1)当r=2cm时, ∵d>r,∴⊙C与AB相离。
即圆心C到AB的距离d=2.4cm。
(2)当r=2.4cm时, ∵d=r, ∴⊙C与AB相切。
(3)当r=3cm时, ∵d<r,∴⊙C与AB相交。
根据三角形面积公式有 CD·AB=AC·BC
=5(cm)
2
2
AB=
解:在Rt△ABC中,
2
2
=
= 2.4(cm)。
∴CD=
=
3.在Rt△ABC,∠C=900,AC=3cm,BC=4cm,以C为圆心,r满足怎样的条件时,C圆与线段AB只有一个交点
2.4
4
3
B
C
A
∟
D
∟
说说收获
直线与圆的位置关系
相 交 相 切 相 离
图 形
公共点个数
公共点名称
直线名称
d与r的关系
d
r
O
l
2 个
交点
割线
1 个
切点
切线
d < r
d = r
d > r
没有
∟
d
r
∟
d
r
判定直线与圆的位置关系的方法有2种:
(1)根据定义,由_____________________的个数来判断;
(2)根据性质,由___________________________的关系来判断。
直线与圆的公共点
圆心到直线的距离d与半径r
在实际应用中,常采用第(2)种方法来判定。
相离
没有公共点
d﹥r
相切
只有一个公共点
d = r
相交
有两个公共点
d < r
2.(必做题)如图:已知∠ AOB=30°,M为OB上一点,且OM=5cm,以M为圆心,以r为半径的圆与直线OA有怎样的位置关系?为什么?
(1)r=2cm; (2)r=4cm; (3)r=2.5cm.
●
O
M
B
A
课堂练习
1.(必做题)P73/练习/1.2.
在第2题中,当r满足什么条件时, ⊙M与射线OA只有一个交点?
拓展训练(选做题)
