23.2中心对称

(共51张PPT)
中心对称
(1) 这些图形有什么共同的特征？
(2) 将上述图形绕其上的某一点旋转180o，
这些图形与原来的图形完全重合吗？
一、中心对称的概念
把一个图形绕着某一个点旋转180°后，如果它能够与另一个图形完全重合，那么称这两个图形关于这个点对称，也叫中心对称。这个点叫做对称中心。这两个图形中的对应点叫做关于中心的对称点。
△ABC与△A`B`C`
关于点O对称,点O是对称中心，对应点A和A`关于点O对称
关于中心对称图形的两个图形，对称点的连线都经过对称中心，并且被对称中心平分。
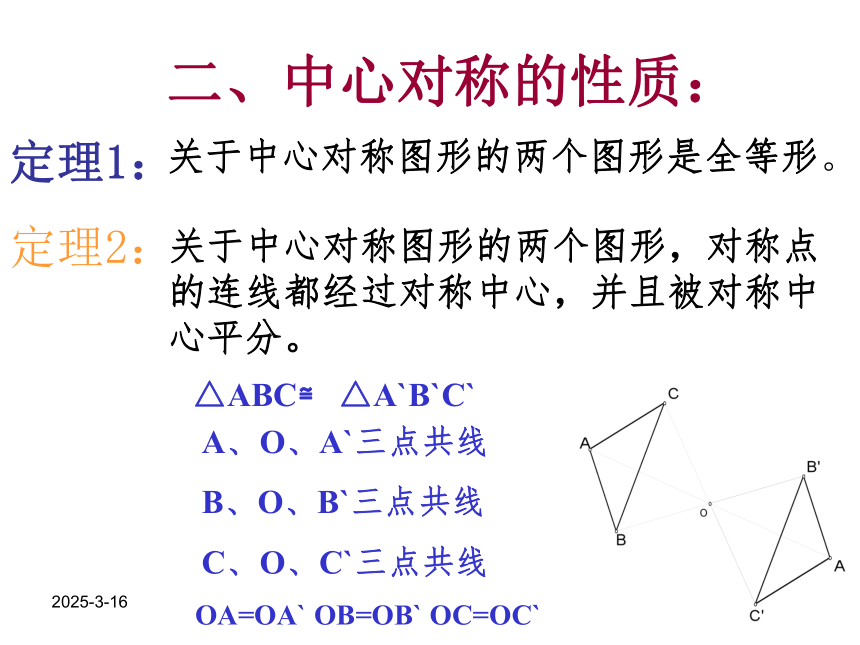
二、中心对称的性质：
定理1：
定理2：
关于中心对称图形的两个图形是全等形。
△ABC≌ △A`B`C`
A、O、A`三点共线
B、O、B`三点共线
C、O、C`三点共线
OA=OA` OB=OB` OC=OC`
轴对称图形
图形
1
2
3
中心对称图形与轴对称图形有什么区别与联系？
4
有一条对称轴
——
直线
有一个对称中心
——
点
图形沿轴对折（翻转
180°
）
图形绕中心旋转
180°
翻转前后的图形完全重合
旋转前后的图形完全重合
对应点的连线被对称轴垂直平分
对称中心平分连结两个对称点的线段
（１）
（２）
（３）
（４）
（５）
（６）
下面图案是中心对称图形吗？若是请指出它们的对称中心，对于图（６），只要把图形绕整个圆的圆心旋转多少度，就能和原图重合。
三、中心对称的作图
A
O
A'
连结OA，
并延长到A’，使OA’=OA，
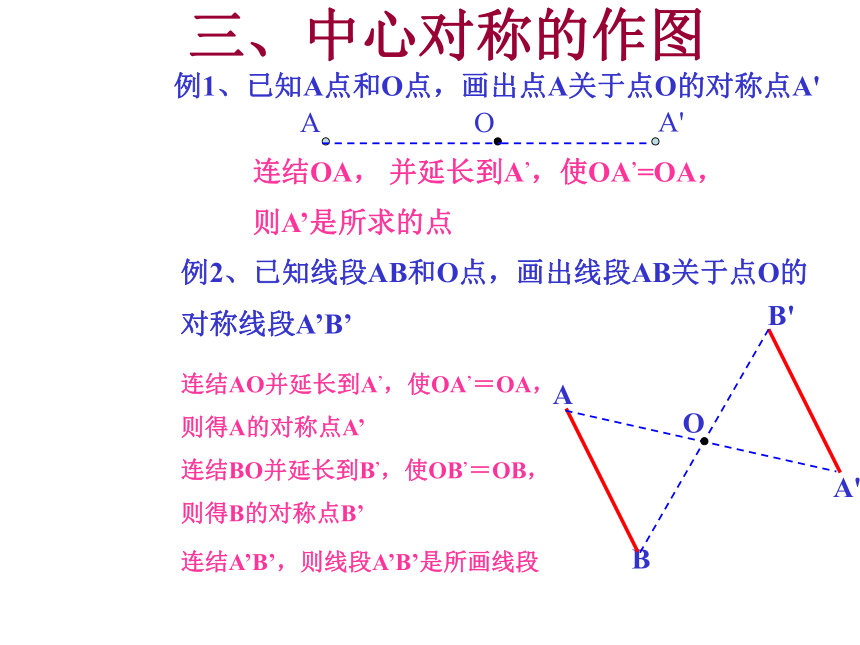
例1、已知A点和O点，画出点A关于点O的对称点A'
则A’是所求的点
例2、已知线段AB和O点，画出线段AB关于点O的
对称线段A’B’
O
A'
B'
A
B
连结AO并延长到A’，使OA’＝OA，
则得A的对称点A’
连结BO并延长到B’，使OB’＝OB，
则得B的对称点B’
连结A’B’，则线段A’B’是所画线段
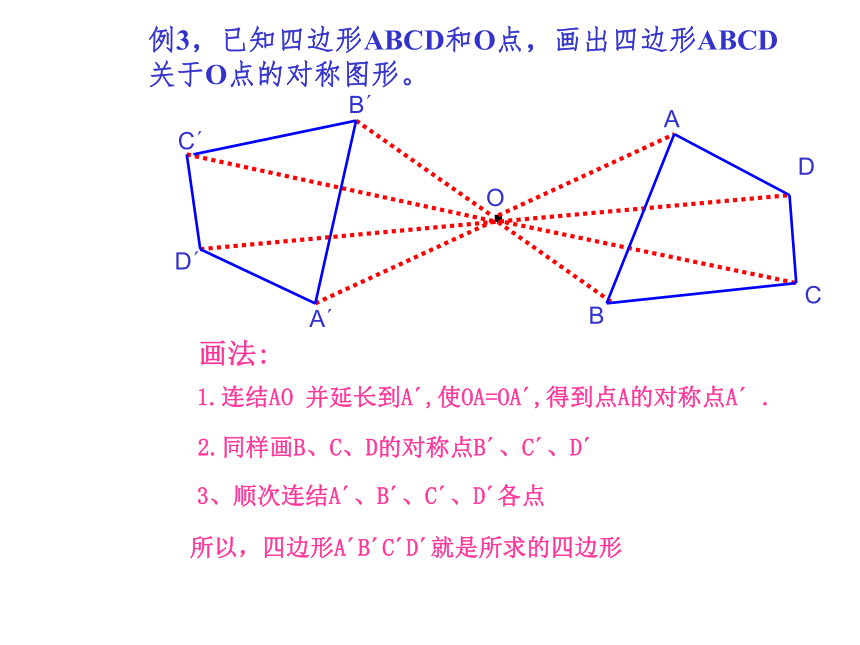
例3，已知四边形ABCD和O点，画出四边形ABCD
关于O点的对称图形。
.
C
D
A
B
D
C
O
A
B
画法:
1.连结AO 并延长到A ,使OA=OA ,得到点A的对称点A .
2.同样画B、C、D的对称点B 、C 、D
3、顺次连结A 、B 、C 、D 各点
所以，四边形A B C D 就是所求的四边形
四、中心对称图形定义
把一个图形绕某一个点旋转180°，如果旋转后的图形能够和原来的图形互相重合，那 么这个图形叫做中心对称图形。这个点就是它的对称中心。
A
B
C
D
O
ABCD是中心对
称图形点 O是对
称中心
中心对称与中心对称图形的区别与联系:
名
称 中心对称 中心对称图形
定
义
性质
区别
联系
如果一个图形绕着一个点旋转180 后的图形能够与原来的图形重合，那么这个图形叫做中心对称形，这个点就是它的对称中心
①两个图形完全重合；
②对应点连线都经过对称中心，并且被对
称中心平分
————
①两个图形的关系
②对称点在两个图形上
①具有某种性质的一个图形
②对称点在一个图形上
若把中心对称图形的两部分分别看作两个图形，则它们成中心对称，若把中心对称的两个图形看作一个整体，则成为中心对称图形。
把一个图形绕着一个点旋转180度后，和另一个图形重合，那么叫做这两个图形关于这点对称，也叫做这两个图形成中心对称，这个点叫做对称中心，这两个图形中的对应点叫做关于中心的对称点。
例1 如图，已知△ ABC与△ CDA
关于点O对称，过点O任作直线EF
分别交AD、BC于点E、F，下面的
结论：①点E和F； B和D是关于
中心O对称； ② 直线BD必经过点
O； ③ 四边形ABCD是中心对称图
形 ； ④四边形DEOC与四边形BF
OA的面积必相等； ⑤△ AOE与△
COF成中心对称，
其中正确的个数为（ ）
A.1个 B.2个 C.3个 D.5个
在26个英文大写正体字母中，哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
随堂练习
判断下列图形是中心对称图形还是轴对称图形 是中心对称图形指明对称中心。
（1）
（2）
（3）
（4）
（5）
（6）
（7）
（8）
名称
图形 中心对称图形 轴对称图形 对称中心，对称轴
线
段
角
等腰三角形
平行四边形
是
是
是
是
不是
不是
不是
是
线段中点
线段的中垂线和线段本身所在的直线
角平分线所在的直线
底边的中垂线
对角线交点
名称
图形
中心对称图形
轴对称图形
对称中心，对称轴
矩形
菱形
正方形
圆
等腰梯形
是
是
是
是
是
是
是
是
是
不是
圆心
边的中垂线
对角线交点
对角线交点
对角线所在直线
对角线交点
对角线所在直线
边的中垂线
直径所在直线
两底的中垂线
1 选择题：
⑴下列图形中即是轴对称图形又是中心对称图形的是（ ）
A 角 B 等边三角形 C 线段 D平行四边形
C
(2) 下列多边形中，是中心对称图形而不是轴对称图形的是（ ）
A平行四边形 B矩形 C菱形 D正方形
A
(3)已知：下列命题中真命题的个数是（ ）
①关于中心对称的两个图形一定不全等
②关于中心对称的两个图形是全等形
③两个全等的图形一定关于中心对称
A 0 B 1 C 2 D 3
B
如果两图形关于某一点成中心对称，那么下列说法:
① 对称点的连线一定经过对称中心
② 对应线段一定相等且平行
③ 将一个图形绕对称中心旋转180度必定与另一个图形重合
④ 一定存在某直线，沿该直线折叠后的两个图形互相重合，其中，正确的是______。
①③
下列说法正确的是：
（1）中心对称与中心对称图形是两个不同的概念，它们既有区别又有联系。
（2）中心对称图形是指两个图形之间的一种对称关系。
（3）中心对称和中心对称图形有一个共同的特点是它们都有且只有一个对称中心。
（4）任何一条经过对称中心的直线都将一个中心对称图形分成两个形状大小完全一样的图形。
解答：（1）正确。由中心对称和中心对称图形的定义得知。
（2）错误。中心对称图形是一个图形本身的性质。
（3）正确。中心对称也好。中心对称图形也好，
都只有一个对称中心，故（3）正确。
（4）正确。由中心对称图形的性质可知。
一、填空
1.如图, ABCD的对角线AC、BD交于O
A
B
C
D
C点
B点
线段CB
平行四边形CDAB
练习
1) A点关于O点的对称点是 ；
2) D点关于O点的对称点是 ；
3)线段AD关于O点的对称线段是
；
4) ABCD关于O点的对称图形是 。
O
二、判断
1.线段的两个端点关于它的中点对称.
√
2.矩形一组对边关于对角线交点对称.
×
3.正方形一组对角的顶点关于对角线交点对称.
√
√
4.关于中心对称的两个图形一定是全等.
√
5.中心对称与中心对称图形是同一个概念.
6.正三角形是中心对称图形.
×
7.矩形、菱形、正方形都是中心对称图形
和轴对称图形.对称轴的交点是对称中心.
√
六、中心对称的特征与实际应用
具有数学美。因为中心对称图形形状匀称美观。所以许多建筑、工艺品、商标常用这种图形作装饰图案。
平稳旋转。具有中心对称图形形状的物体，能够在所在的平面内绕对称中心平稳旋转。所以在生产中，有关旋转的零部件常设计成中心对称图形。
上图表示一根弦的分段振动和整体振动。
雅致
全课总结:
中心对称与中心对称图形两个概念区别和联系
中心对称是 全等图形之间的 ；
中心对称图形是 图形本身成对称的 。
中心对称的两个图形性质
成中心对称的两个图形，对称点的连线都经过 ，并且被对称中心 。
成中心对称的两个图形是 ；
全等形。
对称中心
平分
画已知图形关于某点的中心对称图形关键是
作出各顶点的对称点。
线段、平行四边形、矩形、菱形、正方形、圆
都是 。
两个
一个
位置关系
特性
中心对称图形