人教A版高中数学必修一2.1.2《指数函数及其性质》说课(共24张PPT)课件
文档属性
| 名称 | 人教A版高中数学必修一2.1.2《指数函数及其性质》说课(共24张PPT)课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-14 08:22:08 | ||
图片预览






文档简介
(共24张PPT)
指数函数及其性质
(第1课时)
知识目标
理解指数函数的定义,会判断指数函数,能画出其图象、说出其性质并能简单应用.
能力目标
通过合作交流、自主探索,培养学生观察、分析、归纳等思维能力;体会数形结合、分类讨论思想;增强识图、用图能力.
德育目标
教学目标的确定
使学生学会认识事物的特殊性与一般性的关系,用联系的观点看问题;并引导学生发现数学中的对称美、简洁美。
教材分析
学情分析
教法分析
教学过程
设计说明
学法分析
3.教学重难点
教学重点:指数函数的定义、图像、性质及其简单应用。
教学难点:指数函数图象和性质的发现、总结过程。
教材分析
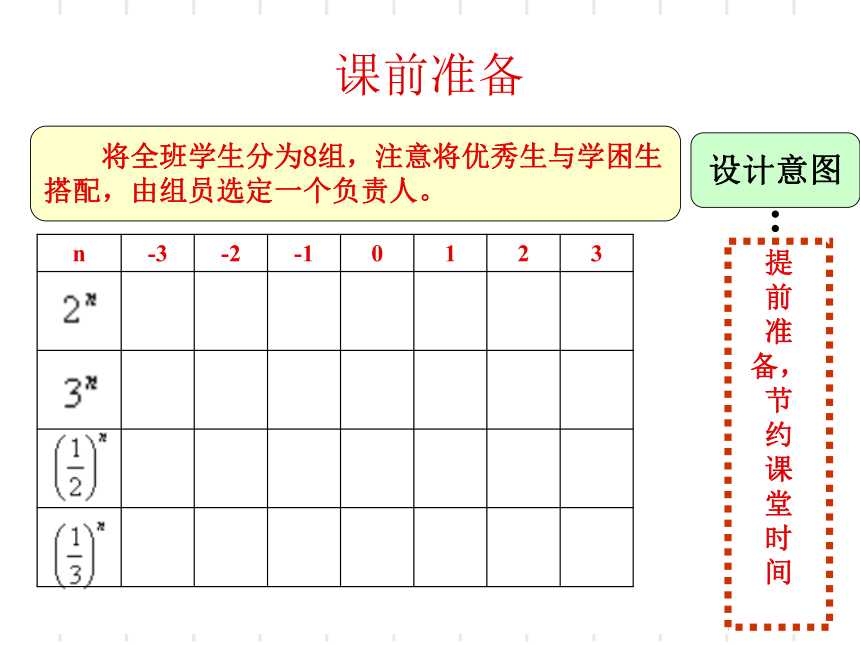
课前准备
将全班学生分为8组,注意将优秀生与学困生
搭配,由组员选定一个负责人。
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
3
2
1
0
-1
-2
-3
n
设计意图
提前准备,节约课堂时间
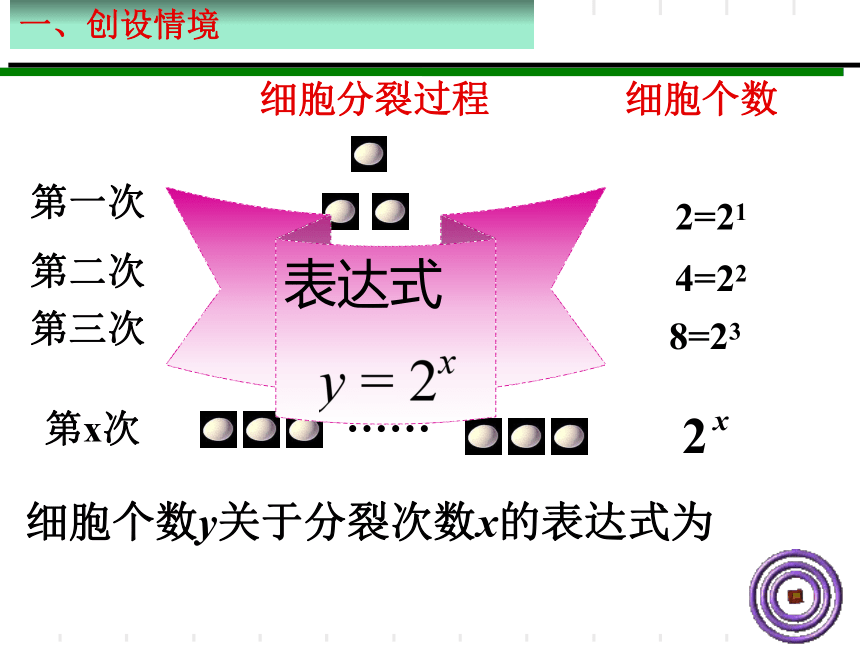
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第x次
……
细胞个数y关于分裂次数x的表达式为
表达式
一、创设情境
创
设
情
境
、
激
发
兴
趣
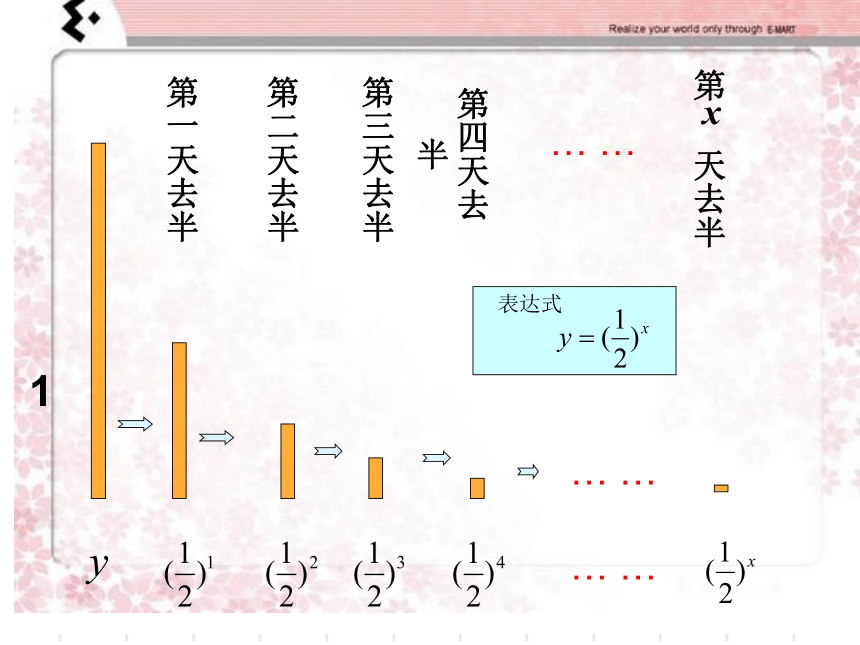
庄
子
第一天去半
第二天去半
第三天去半
第四天去半
第
天去半
…
…
1
表达式
…
…
…
…
前面我们从两个实例中抽象得到两个函数:
1、定义:
这两个函数表达式有何异同?
函数y
=
ax(a?0,且a
?1)叫做指数函数,其中x是自变量
.函数的定义域是R
.
起个什么名字?
注:回顾上一节的内容,我们发现指数
中p可以是有理数也可以是无理数,
所以指数函数的定义域是R。
p
a
二、概念的形成
探究:
三、概念深化、完善认识
?
?
0
1
a
(1)如果
,比如
,这时对于
等,
在实数范围内函数值不存在;
(2)如果
,
;
(3)如果
,
,是常值函数,没有研究的必要;
(4)如果
或
,即
,当
是实数时,
都有意义.
学生思考:判断下列函数哪些是指数函数?
概念上
“咬文嚼字”
牛
刀
小
试
、
巩
固
概
念
教师指导:提醒学生指数函数的定义是形式定义,必须
在形式上一模一样才行,进而得出只有(1)是指数函数。
研究函数的一般思路:
教师指导:
函数的
图象
函数的
性质
特殊的
函数
函数的
定义
用性质
解问题
四、合作互动、探求新知
具体函数图像探究
问题引导:
(1)能用什么方法画出函数
的图像呢?
(2)
你打算对自变量取哪些数呢?
(3)在不影响图像的情况下,取点要保证什么呢?
合作互动、探求新知
教师活动:
?然后用实物投影仪投出学生的作品,再借助多媒体画出这四组指数函数图象。
0
1
1
问题思考:1.底互为倒数的两指数函数图象间的关系?
2.
若把指数函数分类,该如何分?
0
1
1
0
1
1
0
1
0
1
探
求
新
知
、
深
化
理
解
特殊点
定义域
奇偶性
单调性
值域
对称性
y
x
0
·
(0,1)
图象
指数函数
的图象和性质
1.
定义域:
2.
值
域:
3.
过
点:
4.
单调性:
5.
函数值的变化情况:
当
x
<
0时,
0<
y
<1.
图象
R
;
(
0
,
+∞)
;
(
0
,
1)
;
在
R
上是增函数;
当
x
>
0时,
y
>
1.
在R上是减函数
在R上是增函数
单调性
(0,1)
(0,1)
过定点
x
>
0时,0<
y
<1
x
<
0时,y
>
1
x
>
0时,y
>
1
x
<
0时,0<
y
<1
函数值变化情况
R
R
值
域
(0,+∞)
(0,+∞)
定义域
图 象
函
数
(0,+∞)
(0,1)
性质
R
解锁密钥:
指数函数很简单
一瞥一捺记心间
图像恒过(0,1)点
x轴渐近线
是增是减底数观
例2、
比较下列各题中两值的大小
(1)
30.8
,
30.7
(2)0.750.1,0.75-0.1
(2)
0.8-0.1,
1.250.2
(4)
0.250.8
,
0.51.8;
(5)
1.70.3
,
0.93.1
(6)
1.50.3,
0.81.2;
同底比较大小
不同底但可化同底
底不同,指数也不同
同底指数幂比大小,构造指数函数,利用函数单调性
利用函数图像或中间变量进行比较
例1、已知指数函数f(x)的图象过点(3,),
求f(0),
f(1),
f(-3)的值。
五、知识应用
巩固提高
知识应用,巩固提高
练习:
已知下列不等式,比较m,n的大小.
(1)
;(2)
.
(3)
知识的逆用,建立函数思想和分类讨论思想
归
纳
总
结
、
知
识
升
华
知识上
(一)指数函数的定义;
(二)图象及性质;
(三)图象及性质的
简单应用;
方法上
(一)分类讨论;
(二)数形结合;
(三)研究函数的方法.
六、归纳总结
知识升华
布置作业
分层练习
必做题:课本59页,习题2.1、A组第5、6题
补充:(1)已知
,则x的取值范围为
;
(2)已知
,则x的取值范围为
;
(3)已知
,则x的取值范围为
;.
选做题:比较
的大小。
板书设计与评价
指数函数及其性质
(第1课时)
知识目标
理解指数函数的定义,会判断指数函数,能画出其图象、说出其性质并能简单应用.
能力目标
通过合作交流、自主探索,培养学生观察、分析、归纳等思维能力;体会数形结合、分类讨论思想;增强识图、用图能力.
德育目标
教学目标的确定
使学生学会认识事物的特殊性与一般性的关系,用联系的观点看问题;并引导学生发现数学中的对称美、简洁美。
教材分析
学情分析
教法分析
教学过程
设计说明
学法分析
3.教学重难点
教学重点:指数函数的定义、图像、性质及其简单应用。
教学难点:指数函数图象和性质的发现、总结过程。
教材分析
课前准备
将全班学生分为8组,注意将优秀生与学困生
搭配,由组员选定一个负责人。
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
3
2
1
0
-1
-2
-3
n
设计意图
提前准备,节约课堂时间
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第x次
……
细胞个数y关于分裂次数x的表达式为
表达式
一、创设情境
创
设
情
境
、
激
发
兴
趣
庄
子
第一天去半
第二天去半
第三天去半
第四天去半
第
天去半
…
…
1
表达式
…
…
…
…
前面我们从两个实例中抽象得到两个函数:
1、定义:
这两个函数表达式有何异同?
函数y
=
ax(a?0,且a
?1)叫做指数函数,其中x是自变量
.函数的定义域是R
.
起个什么名字?
注:回顾上一节的内容,我们发现指数
中p可以是有理数也可以是无理数,
所以指数函数的定义域是R。
p
a
二、概念的形成
探究:
三、概念深化、完善认识
?
?
0
1
a
(1)如果
,比如
,这时对于
等,
在实数范围内函数值不存在;
(2)如果
,
;
(3)如果
,
,是常值函数,没有研究的必要;
(4)如果
或
,即
,当
是实数时,
都有意义.
学生思考:判断下列函数哪些是指数函数?
概念上
“咬文嚼字”
牛
刀
小
试
、
巩
固
概
念
教师指导:提醒学生指数函数的定义是形式定义,必须
在形式上一模一样才行,进而得出只有(1)是指数函数。
研究函数的一般思路:
教师指导:
函数的
图象
函数的
性质
特殊的
函数
函数的
定义
用性质
解问题
四、合作互动、探求新知
具体函数图像探究
问题引导:
(1)能用什么方法画出函数
的图像呢?
(2)
你打算对自变量取哪些数呢?
(3)在不影响图像的情况下,取点要保证什么呢?
合作互动、探求新知
教师活动:
?然后用实物投影仪投出学生的作品,再借助多媒体画出这四组指数函数图象。
0
1
1
问题思考:1.底互为倒数的两指数函数图象间的关系?
2.
若把指数函数分类,该如何分?
0
1
1
0
1
1
0
1
0
1
探
求
新
知
、
深
化
理
解
特殊点
定义域
奇偶性
单调性
值域
对称性
y
x
0
·
(0,1)
图象
指数函数
的图象和性质
1.
定义域:
2.
值
域:
3.
过
点:
4.
单调性:
5.
函数值的变化情况:
当
x
<
0时,
0<
y
<1.
图象
R
;
(
0
,
+∞)
;
(
0
,
1)
;
在
R
上是增函数;
当
x
>
0时,
y
>
1.
在R上是减函数
在R上是增函数
单调性
(0,1)
(0,1)
过定点
x
>
0时,0<
y
<1
x
<
0时,y
>
1
x
>
0时,y
>
1
x
<
0时,0<
y
<1
函数值变化情况
R
R
值
域
(0,+∞)
(0,+∞)
定义域
图 象
函
数
(0,+∞)
(0,1)
性质
R
解锁密钥:
指数函数很简单
一瞥一捺记心间
图像恒过(0,1)点
x轴渐近线
是增是减底数观
例2、
比较下列各题中两值的大小
(1)
30.8
,
30.7
(2)0.750.1,0.75-0.1
(2)
0.8-0.1,
1.250.2
(4)
0.250.8
,
0.51.8;
(5)
1.70.3
,
0.93.1
(6)
1.50.3,
0.81.2;
同底比较大小
不同底但可化同底
底不同,指数也不同
同底指数幂比大小,构造指数函数,利用函数单调性
利用函数图像或中间变量进行比较
例1、已知指数函数f(x)的图象过点(3,),
求f(0),
f(1),
f(-3)的值。
五、知识应用
巩固提高
知识应用,巩固提高
练习:
已知下列不等式,比较m,n的大小.
(1)
;(2)
.
(3)
知识的逆用,建立函数思想和分类讨论思想
归
纳
总
结
、
知
识
升
华
知识上
(一)指数函数的定义;
(二)图象及性质;
(三)图象及性质的
简单应用;
方法上
(一)分类讨论;
(二)数形结合;
(三)研究函数的方法.
六、归纳总结
知识升华
布置作业
分层练习
必做题:课本59页,习题2.1、A组第5、6题
补充:(1)已知
,则x的取值范围为
;
(2)已知
,则x的取值范围为
;
(3)已知
,则x的取值范围为
;.
选做题:比较
的大小。
板书设计与评价
