苏科版八年级上册数学 6.1函数 教案
文档属性
| 名称 | 苏科版八年级上册数学 6.1函数 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 377.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-14 07:45:51 | ||
图片预览

文档简介
课 题 6.1 函 数 时 间
课 型 新授课 主备
审 核
学习目标 1.通过简单实例,了解常量与变量的意义;
2.通过实例,让学生多角度、多层面地认识和理解函数的意义,感受函数的多种表示形式;
3.能说出一些函数的实例,并能判断两个变量间的关系是否是函数关系.
学习重 难 点 重 点 1.函数概念的建立;
2.判断两个变量间的关系是否是函数关系.
难 点 函数概念中的常量、变量的理解及其对应关系探索.
学 习 过 程
一、预习指导: 1、在某一变化过程中,数值保持 的量叫做常量,可以取不同数值的量叫做
2、一般的,在一个变化的过程中的两个 量x和y,如果对于x的每一个值,y都有 的值与它对应,那么我们称y是x的函数,x是 量.
二、预习作业:
1、经测量,淮安与南京两地的路程s为180千米,当汽车以v千米/时的速度行驶时,t小时到达.
在这变化的过程中,没有变化的量是 , 变化的量是
2、从淮安出发,汽车在高速路上总是以速度v为100千米/时行驶,已行驶路程为s千米,时间为t小时。
在这变化的过程中,没有变化的量是 , 变化的量是
(3)下表中的y是x的函数吗?为什么?
x
1
2
3
4
5
y
±1
±2
±3
±4
±5
三、情境导入:
1、宇宙无时无刻不在变化……
2、神十飞天圆梦……
四、新知探究:
活动一
1.已知某公园门票的价格为50元/人.
(1)2个人进去,需 元;
3个人进去,需 元;
5个人进去,需 元;
(2)在这变化的过程中,没有变化的量是 , 变化的量是
2. 把一根2m长的铁丝围成一个长方形.
(1)填表
宽(m)
0.1
0.2
0.3
…
长(m)
…
(2)在这变化的过程中,没有变化的量是 , 变化的量是
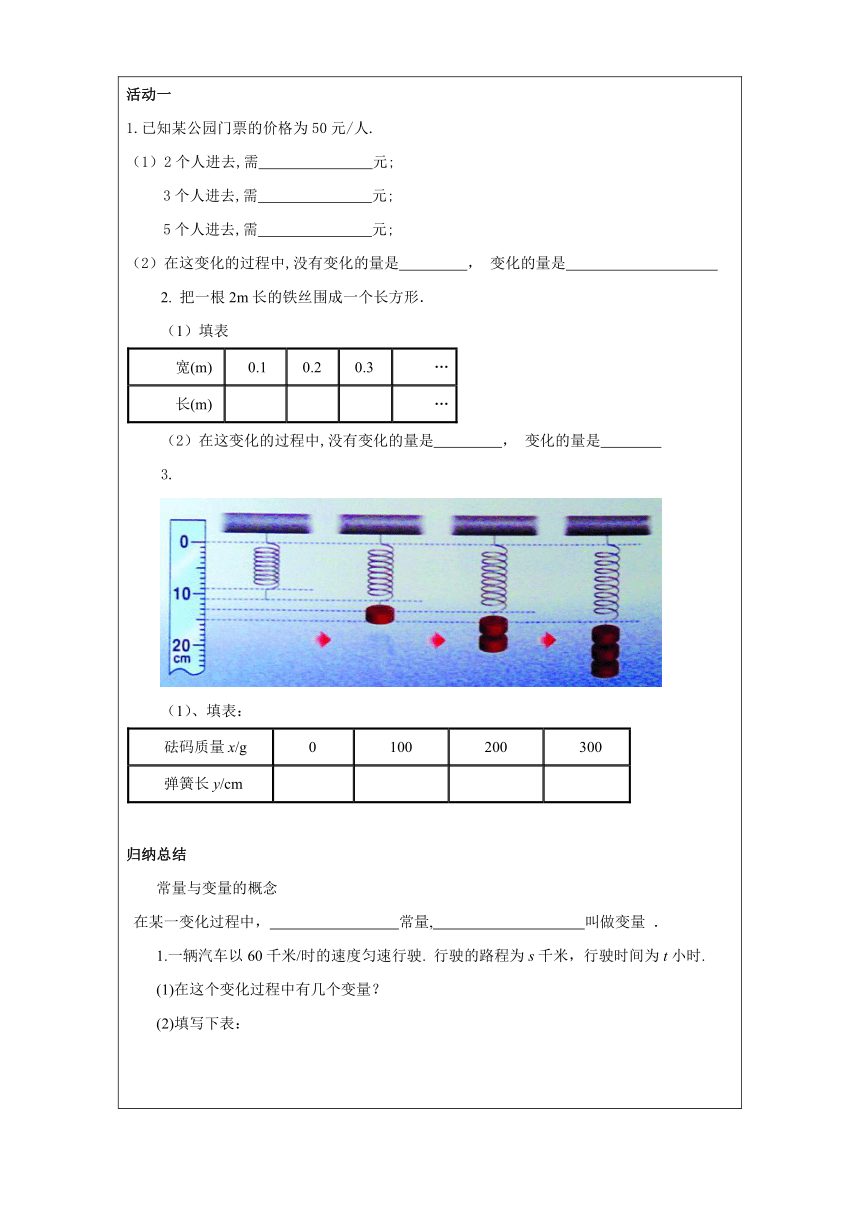
3.
(1)、填表:
砝码质量x/g
0
100
200
300
弹簧长y/cm
归纳总结
常量与变量的概念
在某一变化过程中, 常量, 叫做变量 .
1.一辆汽车以60千米/时的速度匀速行驶. 行驶的路程为s千米,行驶时间为t小时.
(1)在这个变化过程中有几个变量?
(2)填写下表:
t/小时
0
1
1.5
5
…
s/千米
…
(3)变量之间的对应关系是怎样的?
2.工作人员根据水库的水位变化与水库蓄水量变化情况而制作的表格:
水位h(m)
106
120
133
135
…
蓄水量Q(m3)
2.30×107
7.09×107
1.18×108
1.23×108
…
看表格回答:
(1)在这个变化过程中有几个变量?
(2)变量之间的对应关系是怎样的?
3. 如图2,根据搭“小鱼”的条数的变化与所需火柴棒根数的变化的情况,填写右表.
活动二
(1)一个 ; (2)两个 变量;
(3)对于一个变量的每一个值,另一个变量
函数定义
搭“小鱼”的条数n
火柴棒的根数S
1
?8
2 2
?
3
?
4
?
?
?
?
一般地,如果在一个变化的过程中有 变量x和y,并且对于变量x的每一个值,变量y都有 的值与它对应,那么我们称 y是 x的函数,x是 量.
活动三
请你举出一些身边函数的实例,并指出其中的自变量与函数.
五、巩固练习:
(1)按如下的运算程序:输入x→+2→×5→-4→输出y 每输入一个实数x,便可输出一个相应的实数y, y 是 x 的函数吗?为什么?
(2)下面这个表格是否表示y是x的函数?为什么?
x
2
24
25
26
y
2
3
4
5
六、课堂小结
通过本节课的学习,对自己说,你有哪些收获?
课堂作业:
1.下列各变量之间的关系,不能构成函数关系的是( ) .
A.圆的周长与半径;
B.长方形的宽一定,它的面积与长;
C.正方形的面积与周长;
D.等腰三角形的面积与底边长.
2某粮店在某一段时间内以相同的价格出售同一种大米,请问在整个的售米过程中哪些量是变量?哪些量是常量?
2.在圆的周长公式 中,变量是 ,常量是 。
3.在求余角的计算公式为β=900-α中,变量是 ,常量是 。
3.如果用x代表左边的数字,用y代表右边的数字,那么变量y是否是变量x的函数?为什么?
课 型 新授课 主备
审 核
学习目标 1.通过简单实例,了解常量与变量的意义;
2.通过实例,让学生多角度、多层面地认识和理解函数的意义,感受函数的多种表示形式;
3.能说出一些函数的实例,并能判断两个变量间的关系是否是函数关系.
学习重 难 点 重 点 1.函数概念的建立;
2.判断两个变量间的关系是否是函数关系.
难 点 函数概念中的常量、变量的理解及其对应关系探索.
学 习 过 程
一、预习指导: 1、在某一变化过程中,数值保持 的量叫做常量,可以取不同数值的量叫做
2、一般的,在一个变化的过程中的两个 量x和y,如果对于x的每一个值,y都有 的值与它对应,那么我们称y是x的函数,x是 量.
二、预习作业:
1、经测量,淮安与南京两地的路程s为180千米,当汽车以v千米/时的速度行驶时,t小时到达.
在这变化的过程中,没有变化的量是 , 变化的量是
2、从淮安出发,汽车在高速路上总是以速度v为100千米/时行驶,已行驶路程为s千米,时间为t小时。
在这变化的过程中,没有变化的量是 , 变化的量是
(3)下表中的y是x的函数吗?为什么?
x
1
2
3
4
5
y
±1
±2
±3
±4
±5
三、情境导入:
1、宇宙无时无刻不在变化……
2、神十飞天圆梦……
四、新知探究:
活动一
1.已知某公园门票的价格为50元/人.
(1)2个人进去,需 元;
3个人进去,需 元;
5个人进去,需 元;
(2)在这变化的过程中,没有变化的量是 , 变化的量是
2. 把一根2m长的铁丝围成一个长方形.
(1)填表
宽(m)
0.1
0.2
0.3
…
长(m)
…
(2)在这变化的过程中,没有变化的量是 , 变化的量是
3.
(1)、填表:
砝码质量x/g
0
100
200
300
弹簧长y/cm
归纳总结
常量与变量的概念
在某一变化过程中, 常量, 叫做变量 .
1.一辆汽车以60千米/时的速度匀速行驶. 行驶的路程为s千米,行驶时间为t小时.
(1)在这个变化过程中有几个变量?
(2)填写下表:
t/小时
0
1
1.5
5
…
s/千米
…
(3)变量之间的对应关系是怎样的?
2.工作人员根据水库的水位变化与水库蓄水量变化情况而制作的表格:
水位h(m)
106
120
133
135
…
蓄水量Q(m3)
2.30×107
7.09×107
1.18×108
1.23×108
…
看表格回答:
(1)在这个变化过程中有几个变量?
(2)变量之间的对应关系是怎样的?
3. 如图2,根据搭“小鱼”的条数的变化与所需火柴棒根数的变化的情况,填写右表.
活动二
(1)一个 ; (2)两个 变量;
(3)对于一个变量的每一个值,另一个变量
函数定义
搭“小鱼”的条数n
火柴棒的根数S
1
?8
2 2
?
3
?
4
?
?
?
?
一般地,如果在一个变化的过程中有 变量x和y,并且对于变量x的每一个值,变量y都有 的值与它对应,那么我们称 y是 x的函数,x是 量.
活动三
请你举出一些身边函数的实例,并指出其中的自变量与函数.
五、巩固练习:
(1)按如下的运算程序:输入x→+2→×5→-4→输出y 每输入一个实数x,便可输出一个相应的实数y, y 是 x 的函数吗?为什么?
(2)下面这个表格是否表示y是x的函数?为什么?
x
2
24
25
26
y
2
3
4
5
六、课堂小结
通过本节课的学习,对自己说,你有哪些收获?
课堂作业:
1.下列各变量之间的关系,不能构成函数关系的是( ) .
A.圆的周长与半径;
B.长方形的宽一定,它的面积与长;
C.正方形的面积与周长;
D.等腰三角形的面积与底边长.
2某粮店在某一段时间内以相同的价格出售同一种大米,请问在整个的售米过程中哪些量是变量?哪些量是常量?
2.在圆的周长公式 中,变量是 ,常量是 。
3.在求余角的计算公式为β=900-α中,变量是 ,常量是 。
3.如果用x代表左边的数字,用y代表右边的数字,那么变量y是否是变量x的函数?为什么?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
