人教版九年级上册数学 24.1.2垂直于弦的直径 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版九年级上册数学 24.1.2垂直于弦的直径 同步练习(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 266.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-13 00:00:00 | ||
图片预览


文档简介
24.1.2垂直于弦的直径 同步练习
一.选择题
1.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则BE的长为( )
A.2 B.4 C.6 D.8
2.如图,△ABC中,AB=5,AC=4,BC=2,以A为圆心AB为半径作圆A,延长BC交圆A于点D,则CD长为( )
A.5 B.4 C. D.2
3.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm B.10cm C.16cm D.20cm
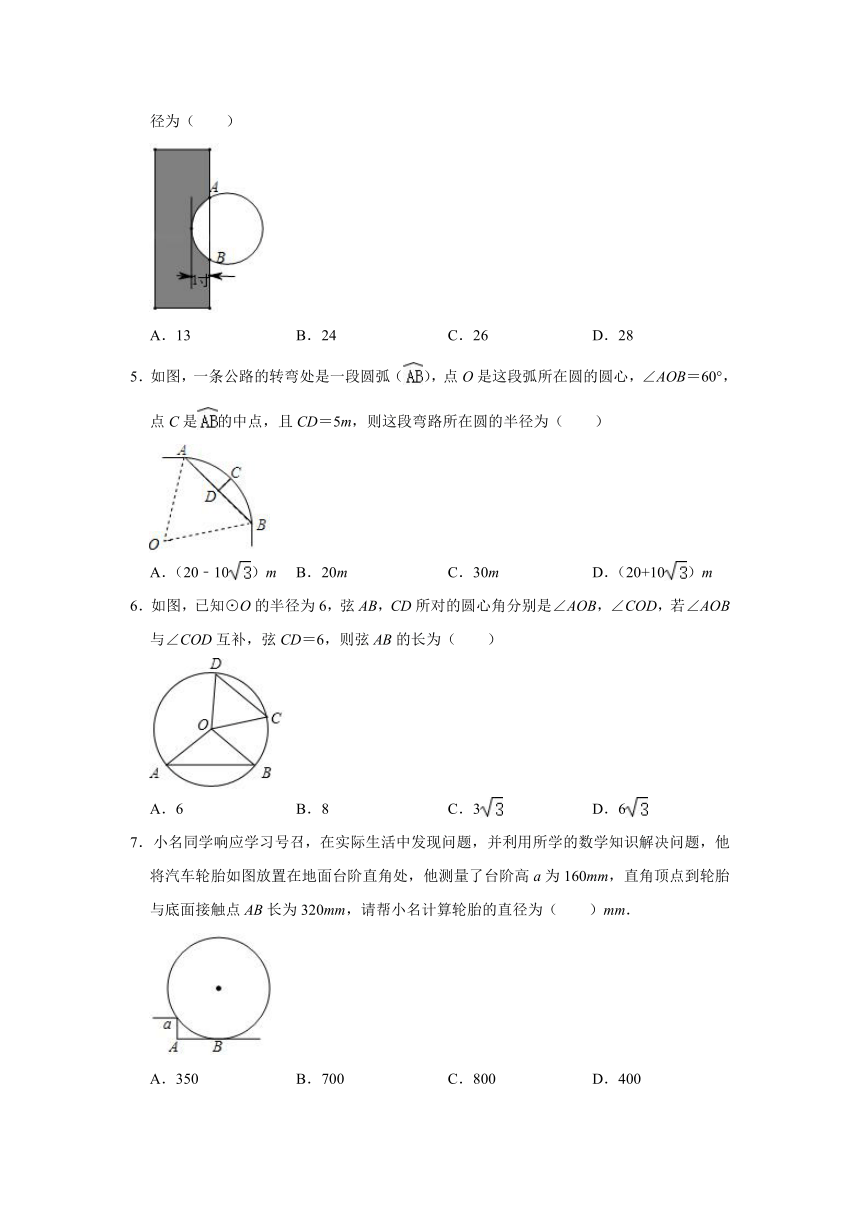
4.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为( )
A.13 B.24 C.26 D.28
5.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,∠AOB=60°,点C是的中点,且CD=5m,则这段弯路所在圆的半径为( )
A.(20﹣10)m B.20m C.30m D.(20+10)m
6.如图,已知⊙O的半径为6,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A.6 B.8 C.3 D.6
7.小名同学响应学习号召,在实际生活中发现问题,并利用所学的数学知识解决问题,他将汽车轮胎如图放置在地面台阶直角处,他测量了台阶高a为160mm,直角顶点到轮胎与底面接触点AB长为320mm,请帮小名计算轮胎的直径为( )mm.
A.350 B.700 C.800 D.400
8.如图,⊙O中,弦AB⊥CD于E,若已知AD=9,BC=12,则⊙O的半径为( )
A.5.5 B.6 C.7.5 D.8
9.如图,AB是⊙O的弦,半径OD⊥AB于点C,AE为直径,AB=8,CD=2,则线段CE的长为( )
A. B.8 C. D.
10.如图,⊙O的直径AB与弦CD相交于点P,且∠APC=45°,若PC2+PD2=8,则⊙O的半径为( )
A. B.2 C.2 D.4
二.填空题
11.已知⊙O的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为 cm.
12.在半径为的⊙O中,弦AB垂直于弦CD,垂足为P,AB=CD=4,则S△ACP= .
13.如图,射线PB,PD分别交圆O于点A,B和点C,D,且AB=CD=8.已知圆O半径等于5,OA∥PC,则OP的长度为 .
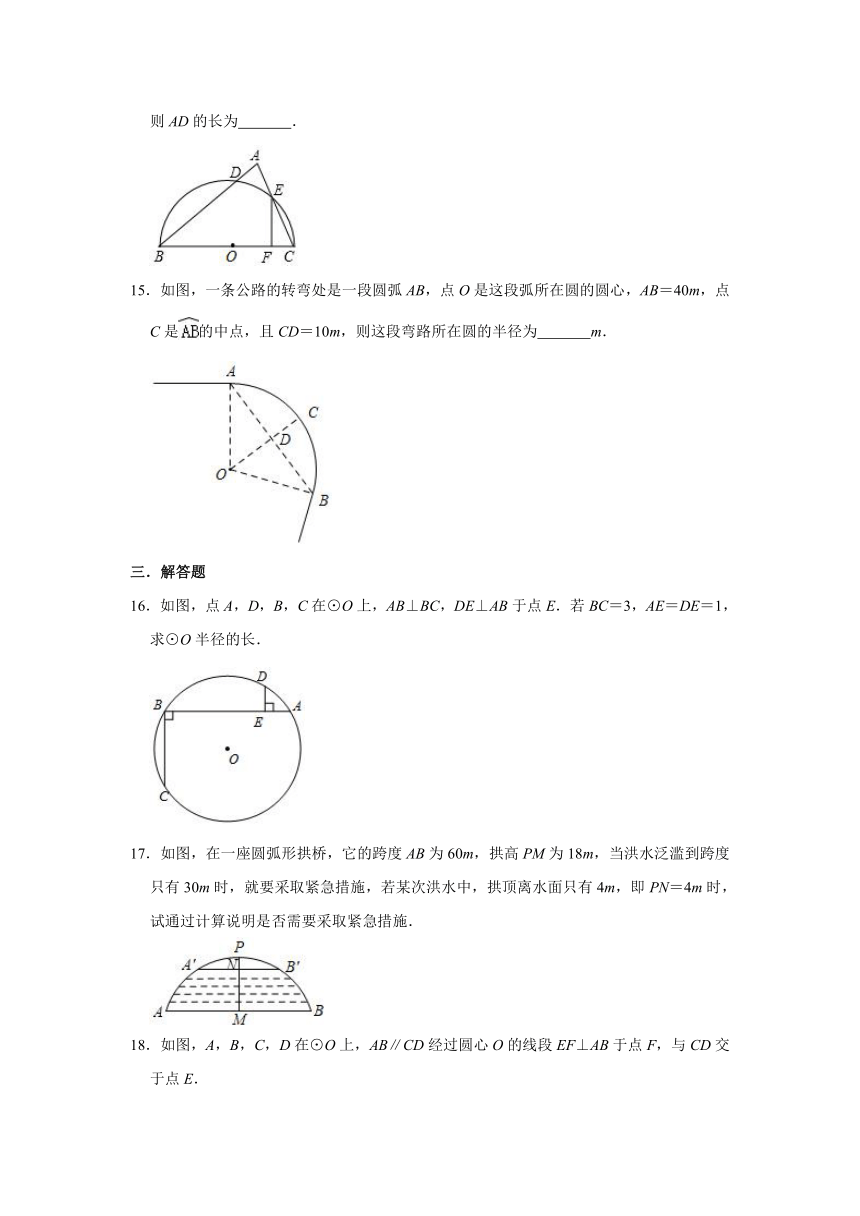
14.如图,BC为半圆O的直径,EF⊥BC于点F,且BF:FC=5:1,若AB=8,AE=2,则AD的长为 .
15.如图,一条公路的转弯处是一段圆弧AB,点O是这段弧所在圆的圆心,AB=40m,点C是的中点,且CD=10m,则这段弯路所在圆的半径为 m.
三.解答题
16.如图,点A,D,B,C在⊙O上,AB⊥BC,DE⊥AB于点E.若BC=3,AE=DE=1,求⊙O半径的长.
17.如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有4m,即PN=4m时,试通过计算说明是否需要采取紧急措施.
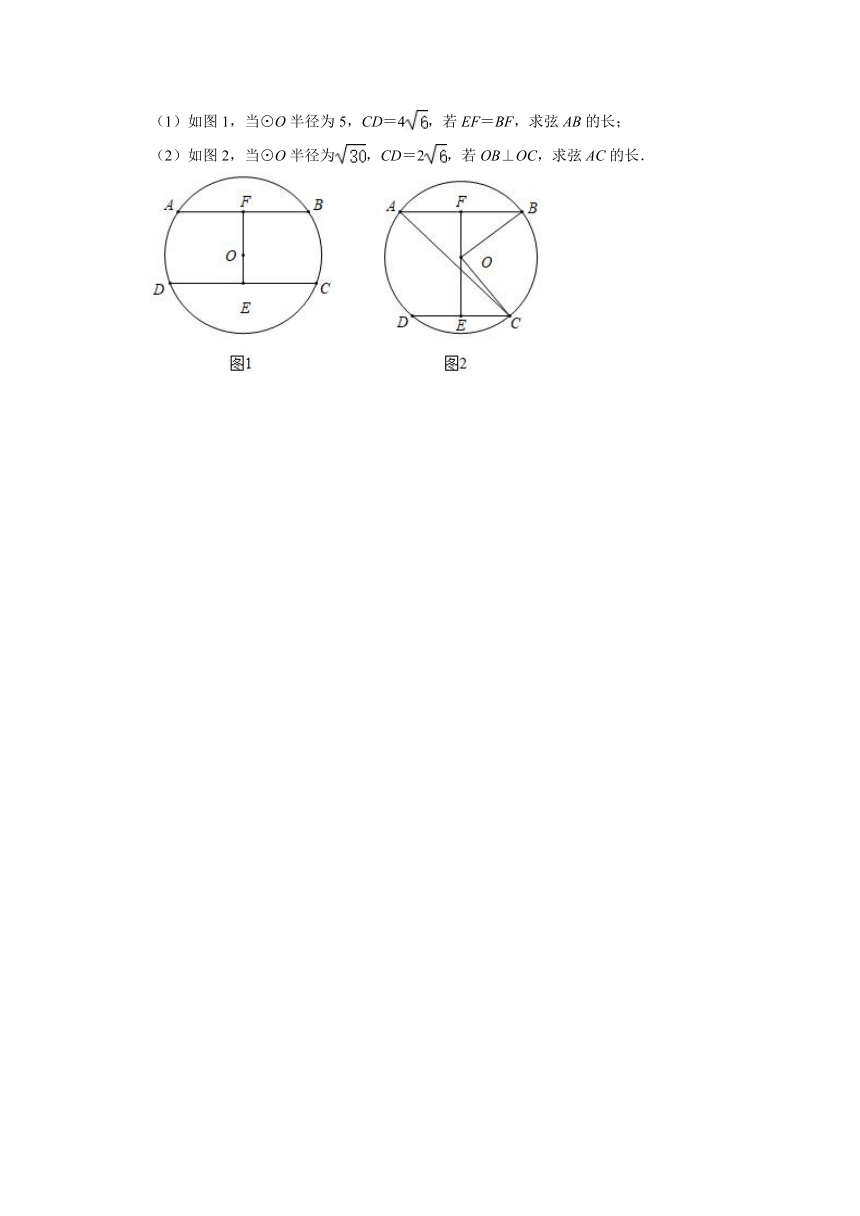
18.如图,A,B,C,D在⊙O上,AB∥CD经过圆心O的线段EF⊥AB于点F,与CD交于点E.
(1)如图1,当⊙O半径为5,CD=4,若EF=BF,求弦AB的长;
(2)如图2,当⊙O半径为,CD=2,若OB⊥OC,求弦AC的长.
参考答案
1.解:∵CE=2,DE=8,
∴CD=10,
∴OB=5,
∴OE=3,
∵AB⊥CD,
∴在△OBE中,BE===4,
故选:B.
2.解:如图,过点A作AE⊥BD于点E,连接AD,
∴AD=AB=5,
根据垂径定理,得
DE=BE,
∴CE=BE﹣BC=DE﹣2,
根据勾股定理,得
AD2﹣DE2=AC2﹣CE2,
∴52﹣DE2=42﹣(DE﹣2)2,
解得DE=,
∴CD=DE+CE=2DE﹣2=.
故选:C.
3.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
4.解:设圆心为O,过O作OC⊥AB于C,交⊙O于D,连接OA,如图所示:
∴AC=AB=×10=5,
设⊙O的半径为r寸,
在Rt△ACO中,OC=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸,
故选:C.
5.解:∵点O是这段弧所在圆的圆心,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB,
设AB=OB=OA=rm,
∵点C是的中点,
∴OC⊥AB,
∴C,D,O三点共线,
∴AD=DB=rm,
在Rt△AOD中,
∴OD=r,
∵OD+CD=OC,
∴r+5=r,
解得:r=(20+10)m,
∴这段弯路的半径为(20+10)m
故选:D.
6.解:作OE⊥AB于点E,
∵⊙O的半径为6,弦CD=6,
∴OC=OD=CD,
∴△DOC是等边三角形,
∴∠DOC=60°,
∵∠AOB与∠COD互补,
∴∠AOB=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵OA=6,OE⊥AB,
∴AE=OA?cos30°=6×=3,
∴AB=2AE=6,
故选:D.
7.解:如图,连接OB,OC,作CD⊥OB于D.
设⊙O半径为xmm,在Rt△OCD中,
由勾股定理得方程,(x﹣160)2+3202=x2,
解得,x=400,
∴2x=800,
答:车轱辘的直径为800mm.
故选:C.
8.解:连接DO并延长DO交圆O于点F,连接BD,AF,BF,
∵∠DAE=∠DFB,∠AED=∠FBD=90°,
∴∠ADC=∠FDB,
∴∠ADF=∠CDB,
∴,
∴AF=BC=12,
∵∠DAF=90°,
∴DF=,
∴⊙O的半径为7.5.
故选:C.
9.解:连结BE,如图,
∵OD⊥弦AB,AB=8,
∴AC=AB=4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,
r2=(r﹣2)2+42,
解得:r=5,
∴AE=2r=10;
∵OD=5,CD=2,
∴OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE===2.
故选:D.
10.解:作CM⊥AB于M,DN⊥AB于N,连接OC,OD,
∴∠NDP=∠MCP=∠APC=45°
又∵OC=OD,
∴∠ODP=∠OCP,
∵∠COM=45°+∠OCD,∠ODB=45°+∠ODC,
∴∠NDO=∠COM,
在Rt△ODN与Rt△COM中,
,
∴Rt△ODN≌Rt△COM,
∴ON=CM=PM,OM=ND=PN
又∵OC2=CM2+OM2,OD2=DN2+ON2
∴OC2=CM2+PN2,OD2=DN2+PM2
∴OC2+OD2=CM2+PN2+DN2+PM2=PC2+PD2=8
∴OC2=4,
∴OC=2,
故选:B.
11.解:如图,作OC⊥AB于C,连接OA,
则AC=BC=AB=5,
在Rt△OAC中,OC==12,
所以圆心O到AB的距离为12cm.
故答案为12.
12.解:作OE⊥AB于E,OF⊥CD于F,连结OD、OB,
则AE=BE=AB=2,DF=CF=CD=2,
如图1,
在Rt△OBE中,∵OB=,BE=2,
∴OE==1,
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
∴PE=PF=1,
∴PA=PC=1,
∴S△APC==;
如图2,
同理:S△APC==;
如图3,
同理:S△APC==;
故答案为:或或.
13.解:作OE⊥AB于E,OF⊥CD于F,连接OP,如图,
∵AB=CD,
∴OE=OF,
而OE⊥AB,OF⊥CD,
∴PO平分∠BPD,
∴∠APO=∠OPC,
∵OA∥PC,
∴∠AOP=∠OPC,
∴∠APO=∠AOP,
∴PA=AO=5,
∵OE⊥AB,
∴AE=BE=AB=4,
在Rt△AOE中,OE==3,
在Rt△POE中,PO==3.
故答案为3.
14.解:连接BE.
∵BC是直径.
∴∠AEB=∠BEC=90°
在直角△ABE中,根据勾股定理可得:BE2=AB2﹣AE2=82﹣22=60.
∵=5
∴设FC=x,则BF=5x,BC=6x.
又∵BE2=BF?BC
即:30x2=60
解得:x=,
∴EC2=FC?BC=6x2=12
∴EC=2,
∴AC=AE+EC=2+2,
∵AD?AB=AE?AC
∴AD===.
故答案为.
15.解:∵OC⊥AB,
∴AD=DB=20m,
在Rt△AOD中,OA2=OD2+AD2,
设半径为r得:r2=(r﹣10)2+202,
解得:r=25m,
∴这段弯路的半径为25m.
故答案为:25.
16.解:如图,连接AD,AC,连接CD与AB交于点F,
∵AB⊥BC,
∴∠ABC=90°.
∴AC为直径.
∴∠ADC=90°.
∵AE=DE,DE⊥AB,
∴∠DAB=∠ADE=45°.
∴∠BCF=∠DAB=45°.
∴BC=BF=3.
在△ADF中,∠DAB=∠AFD=45°,
∴EF=ED=1.
∴AB=5.
∴AC==.
∴⊙O半径的长.
17.解:设圆弧所在圆的圆心为O,连接OA、OA′,设半径为x米,
则OA=OA′=OP,
由垂径定理可知AM=BM,A′N=B′N,
∵AB=60米,
∴AM=30米,且OM=OP﹣PM=(x﹣18)米,
在Rt△AOM中,由勾股定理可得AO2=OM2+AM2,
即x2=(x﹣18)2+302,解得x=34,
∴ON=OP﹣PN=34﹣4=30(米),
在Rt△A′ON中,由勾股定理可得A′N===16(米),
∴A′B′=32米>30米,
∴不需要采取紧急措施.
18.解:(1)如图1中,连接OB,OC.设BF=EF=x,OF=y.
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴∠CEF=∠BFO=90°
∴AF=BF=x,DE=EC=2,
根据勾股定理可得:,
解得(舍弃)或,
∴BF=4,AB=2BF=8.
(2)如图2中,作CH⊥AB于H.
∵OB⊥OC,
∴∠A=∠BOC=45°,
∵AH⊥CH,
∴△ACH是等腰直角三角形,
∵AC=CH,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∠CEF=∠EFH=∠CHF=90°,
∴四边形EFHC是矩形,
∴CH=EF,
在Rt△OEC中,∵EC=,OC=,
OE===2,
∵∠EOC+∠OCE=90°,∠EOC+∠FOB=90°,
∴∠FOB=∠ECO,
∵OB=OC,
∴△OFB≌△CEO(AAS),
∴OF=EC=,
∴CH=EF=3,
∴AC=EF=6.
一.选择题
1.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则BE的长为( )
A.2 B.4 C.6 D.8
2.如图,△ABC中,AB=5,AC=4,BC=2,以A为圆心AB为半径作圆A,延长BC交圆A于点D,则CD长为( )
A.5 B.4 C. D.2
3.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm B.10cm C.16cm D.20cm
4.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为( )
A.13 B.24 C.26 D.28
5.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,∠AOB=60°,点C是的中点,且CD=5m,则这段弯路所在圆的半径为( )
A.(20﹣10)m B.20m C.30m D.(20+10)m
6.如图,已知⊙O的半径为6,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A.6 B.8 C.3 D.6
7.小名同学响应学习号召,在实际生活中发现问题,并利用所学的数学知识解决问题,他将汽车轮胎如图放置在地面台阶直角处,他测量了台阶高a为160mm,直角顶点到轮胎与底面接触点AB长为320mm,请帮小名计算轮胎的直径为( )mm.
A.350 B.700 C.800 D.400
8.如图,⊙O中,弦AB⊥CD于E,若已知AD=9,BC=12,则⊙O的半径为( )
A.5.5 B.6 C.7.5 D.8
9.如图,AB是⊙O的弦,半径OD⊥AB于点C,AE为直径,AB=8,CD=2,则线段CE的长为( )
A. B.8 C. D.
10.如图,⊙O的直径AB与弦CD相交于点P,且∠APC=45°,若PC2+PD2=8,则⊙O的半径为( )
A. B.2 C.2 D.4
二.填空题
11.已知⊙O的半径为13cm,弦AB的长为10cm,则圆心O到AB的距离为 cm.
12.在半径为的⊙O中,弦AB垂直于弦CD,垂足为P,AB=CD=4,则S△ACP= .
13.如图,射线PB,PD分别交圆O于点A,B和点C,D,且AB=CD=8.已知圆O半径等于5,OA∥PC,则OP的长度为 .
14.如图,BC为半圆O的直径,EF⊥BC于点F,且BF:FC=5:1,若AB=8,AE=2,则AD的长为 .
15.如图,一条公路的转弯处是一段圆弧AB,点O是这段弧所在圆的圆心,AB=40m,点C是的中点,且CD=10m,则这段弯路所在圆的半径为 m.
三.解答题
16.如图,点A,D,B,C在⊙O上,AB⊥BC,DE⊥AB于点E.若BC=3,AE=DE=1,求⊙O半径的长.
17.如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有4m,即PN=4m时,试通过计算说明是否需要采取紧急措施.
18.如图,A,B,C,D在⊙O上,AB∥CD经过圆心O的线段EF⊥AB于点F,与CD交于点E.
(1)如图1,当⊙O半径为5,CD=4,若EF=BF,求弦AB的长;
(2)如图2,当⊙O半径为,CD=2,若OB⊥OC,求弦AC的长.
参考答案
1.解:∵CE=2,DE=8,
∴CD=10,
∴OB=5,
∴OE=3,
∵AB⊥CD,
∴在△OBE中,BE===4,
故选:B.
2.解:如图,过点A作AE⊥BD于点E,连接AD,
∴AD=AB=5,
根据垂径定理,得
DE=BE,
∴CE=BE﹣BC=DE﹣2,
根据勾股定理,得
AD2﹣DE2=AC2﹣CE2,
∴52﹣DE2=42﹣(DE﹣2)2,
解得DE=,
∴CD=DE+CE=2DE﹣2=.
故选:C.
3.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
4.解:设圆心为O,过O作OC⊥AB于C,交⊙O于D,连接OA,如图所示:
∴AC=AB=×10=5,
设⊙O的半径为r寸,
在Rt△ACO中,OC=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸,
故选:C.
5.解:∵点O是这段弧所在圆的圆心,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB,
设AB=OB=OA=rm,
∵点C是的中点,
∴OC⊥AB,
∴C,D,O三点共线,
∴AD=DB=rm,
在Rt△AOD中,
∴OD=r,
∵OD+CD=OC,
∴r+5=r,
解得:r=(20+10)m,
∴这段弯路的半径为(20+10)m
故选:D.
6.解:作OE⊥AB于点E,
∵⊙O的半径为6,弦CD=6,
∴OC=OD=CD,
∴△DOC是等边三角形,
∴∠DOC=60°,
∵∠AOB与∠COD互补,
∴∠AOB=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵OA=6,OE⊥AB,
∴AE=OA?cos30°=6×=3,
∴AB=2AE=6,
故选:D.
7.解:如图,连接OB,OC,作CD⊥OB于D.
设⊙O半径为xmm,在Rt△OCD中,
由勾股定理得方程,(x﹣160)2+3202=x2,
解得,x=400,
∴2x=800,
答:车轱辘的直径为800mm.
故选:C.
8.解:连接DO并延长DO交圆O于点F,连接BD,AF,BF,
∵∠DAE=∠DFB,∠AED=∠FBD=90°,
∴∠ADC=∠FDB,
∴∠ADF=∠CDB,
∴,
∴AF=BC=12,
∵∠DAF=90°,
∴DF=,
∴⊙O的半径为7.5.
故选:C.
9.解:连结BE,如图,
∵OD⊥弦AB,AB=8,
∴AC=AB=4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,
r2=(r﹣2)2+42,
解得:r=5,
∴AE=2r=10;
∵OD=5,CD=2,
∴OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE===2.
故选:D.
10.解:作CM⊥AB于M,DN⊥AB于N,连接OC,OD,
∴∠NDP=∠MCP=∠APC=45°
又∵OC=OD,
∴∠ODP=∠OCP,
∵∠COM=45°+∠OCD,∠ODB=45°+∠ODC,
∴∠NDO=∠COM,
在Rt△ODN与Rt△COM中,
,
∴Rt△ODN≌Rt△COM,
∴ON=CM=PM,OM=ND=PN
又∵OC2=CM2+OM2,OD2=DN2+ON2
∴OC2=CM2+PN2,OD2=DN2+PM2
∴OC2+OD2=CM2+PN2+DN2+PM2=PC2+PD2=8
∴OC2=4,
∴OC=2,
故选:B.
11.解:如图,作OC⊥AB于C,连接OA,
则AC=BC=AB=5,
在Rt△OAC中,OC==12,
所以圆心O到AB的距离为12cm.
故答案为12.
12.解:作OE⊥AB于E,OF⊥CD于F,连结OD、OB,
则AE=BE=AB=2,DF=CF=CD=2,
如图1,
在Rt△OBE中,∵OB=,BE=2,
∴OE==1,
同理可得OF=1,
∵AB⊥CD,
∴四边形OEPF为矩形,
∴PE=PF=1,
∴PA=PC=1,
∴S△APC==;
如图2,
同理:S△APC==;
如图3,
同理:S△APC==;
故答案为:或或.
13.解:作OE⊥AB于E,OF⊥CD于F,连接OP,如图,
∵AB=CD,
∴OE=OF,
而OE⊥AB,OF⊥CD,
∴PO平分∠BPD,
∴∠APO=∠OPC,
∵OA∥PC,
∴∠AOP=∠OPC,
∴∠APO=∠AOP,
∴PA=AO=5,
∵OE⊥AB,
∴AE=BE=AB=4,
在Rt△AOE中,OE==3,
在Rt△POE中,PO==3.
故答案为3.
14.解:连接BE.
∵BC是直径.
∴∠AEB=∠BEC=90°
在直角△ABE中,根据勾股定理可得:BE2=AB2﹣AE2=82﹣22=60.
∵=5
∴设FC=x,则BF=5x,BC=6x.
又∵BE2=BF?BC
即:30x2=60
解得:x=,
∴EC2=FC?BC=6x2=12
∴EC=2,
∴AC=AE+EC=2+2,
∵AD?AB=AE?AC
∴AD===.
故答案为.
15.解:∵OC⊥AB,
∴AD=DB=20m,
在Rt△AOD中,OA2=OD2+AD2,
设半径为r得:r2=(r﹣10)2+202,
解得:r=25m,
∴这段弯路的半径为25m.
故答案为:25.
16.解:如图,连接AD,AC,连接CD与AB交于点F,
∵AB⊥BC,
∴∠ABC=90°.
∴AC为直径.
∴∠ADC=90°.
∵AE=DE,DE⊥AB,
∴∠DAB=∠ADE=45°.
∴∠BCF=∠DAB=45°.
∴BC=BF=3.
在△ADF中,∠DAB=∠AFD=45°,
∴EF=ED=1.
∴AB=5.
∴AC==.
∴⊙O半径的长.
17.解:设圆弧所在圆的圆心为O,连接OA、OA′,设半径为x米,
则OA=OA′=OP,
由垂径定理可知AM=BM,A′N=B′N,
∵AB=60米,
∴AM=30米,且OM=OP﹣PM=(x﹣18)米,
在Rt△AOM中,由勾股定理可得AO2=OM2+AM2,
即x2=(x﹣18)2+302,解得x=34,
∴ON=OP﹣PN=34﹣4=30(米),
在Rt△A′ON中,由勾股定理可得A′N===16(米),
∴A′B′=32米>30米,
∴不需要采取紧急措施.
18.解:(1)如图1中,连接OB,OC.设BF=EF=x,OF=y.
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴∠CEF=∠BFO=90°
∴AF=BF=x,DE=EC=2,
根据勾股定理可得:,
解得(舍弃)或,
∴BF=4,AB=2BF=8.
(2)如图2中,作CH⊥AB于H.
∵OB⊥OC,
∴∠A=∠BOC=45°,
∵AH⊥CH,
∴△ACH是等腰直角三角形,
∵AC=CH,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∠CEF=∠EFH=∠CHF=90°,
∴四边形EFHC是矩形,
∴CH=EF,
在Rt△OEC中,∵EC=,OC=,
OE===2,
∵∠EOC+∠OCE=90°,∠EOC+∠FOB=90°,
∴∠FOB=∠ECO,
∵OB=OC,
∴△OFB≌△CEO(AAS),
∴OF=EC=,
∴CH=EF=3,
∴AC=EF=6.
同课章节目录
