人教版高一物理必修二5.5向心加速度(23张PPT)
文档属性
| 名称 | 人教版高一物理必修二5.5向心加速度(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-14 07:59:25 | ||
图片预览







文档简介
(共23张PPT)
5
向心加速度
回顾:牛顿第一定律
牛顿第二定律
做圆周运动的物体是否一定受力?
那么做匀速圆周运动的物体所受合外力方向有什么特点?
如果物体不受力
做匀速直线运动或静止
做圆周运动的物体
变速曲线运动
根据牛顿第二定律(同样适用于曲线运动),即合外力一定不为零。
一定存在加速度
速度方向一定改变
地球受到什么力的作用?
这个力可能沿什么方向?
讨论
应该受到指向太阳的引力作用
因此,根据牛二(力与加速度具有同向性),地球的加速度的方向指向太阳
感知加速度的方向
V
F
F
F
V
V
结论:做匀速圆周运动的卫星,合外力方向
指向圆心(地心),与速度V垂直
卫星绕地球(行星)的运动
小球受到几个力的作用?
这几个力的合力沿什么方向?
小球受到重力、支持力和绳子的拉力三个力的作用,其合力即为绳子的拉力,其方向指向圆心
G
N
F拉
因此,小球的加速度的方向指向圆心
结论
做匀速圆周运动的物体,其加速度的方向时刻指向圆心,这个加速度叫向心加速度
O
B
A
vA
vB
vA
Δv
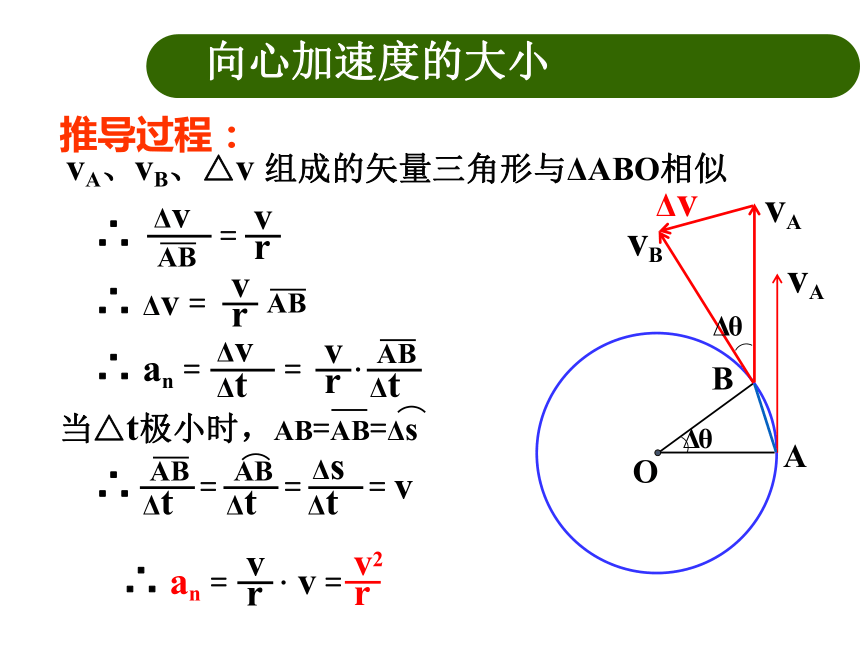
vA、vB、△v
组成的矢量三角形与ΔABO相似
∴
=
AB
Δv
v
r
∴
Δv
=
AB
v
r
∴
an
=
=
·
AB
v
r
Δv
Δt
Δt
当△t极小时,AB=AB=Δs
∴
=
=
=
v
AB
Δs
Δt
Δt
AB
Δt
∴
an
=
·
v
=
v
r
v2
r
Δ
θ
Δ
θ
推导过程:
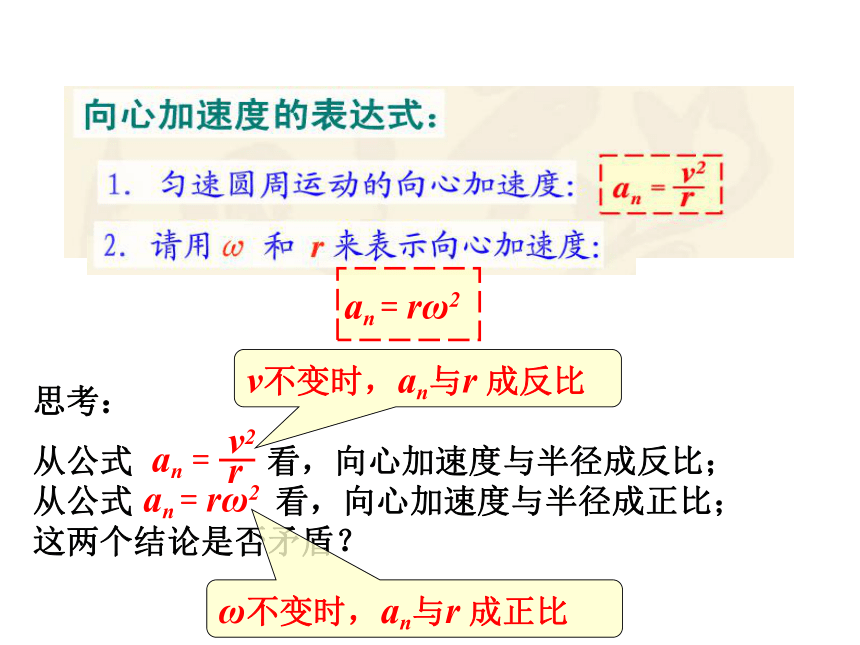
向心加速度的大小
an
=
rω2
思考:
从公式
看,向心加速度与半径成反比;从公式
看,向心加速度与半径成正比;这两个结论是否矛盾?
an
=
v2
r
an
=
rω2
v不变时,an与r
成反比
ω不变时,an与r
成正比
an
=
vω
an
=
r
4π2
T
2
an
=
4π2
f
2r
=4π2
n2r
1、定义:
做匀速圆周运动的物体,
加速度始终
指向圆心,这个瞬时加速度就叫向心加速度。
3、物理意义:描述线速度的方向变化的快慢;
只改变线速度方向,不改变其大小
4、方向:
总是指向圆心,时刻变化,
是一个变加速度;
5、匀速圆周运动性质:变加速曲线运动;
四、匀速圆周运动的向心加速度
2、大小:
an
=
rω2
an
=
v2
r
谢谢!
五、变速圆周运动的加速度
竖直平面内的圆周运动一般是变速圆周运动(如重物在细绳/轻杆的作用下做圆周运动),运动的速度大小和方向在不断发生变化,运动过程复杂,合外力不仅要改变运动方向,还要改变速度大小。
练习1
如图所示,半径为R的圆盘绕过圆心的竖直轴OO′匀速转动,在距轴为r处有一竖直杆,杆上用长为L的细线悬挂一小球.当圆盘以角速度ω匀速转动时,小球也以同样的角速度做匀速圆周运动,这时细线与竖直方向的夹角为θ,则小球的向心加速度大小为(
)
A.
B.
C.
D.
D
如图所示,一个皮带传动减速装置,轮A和轮B共轴固定在一起组成一个塔形轮.各轮半径之比RA∶RB∶RC∶RD=2∶1∶1∶2,则运转过程中,轮C边缘上一点和轮D边缘上一点的线速度之比为__________,角速度之比为__________向心加速度之比为__________.
练习2
答案:
2∶1
4∶1
8∶1
如图所示,细绳的一端固定,另一端系一小球,让小球在竖直面内做圆周运动,关于小球运动到P点时的加速度方向,下列图中可能的是( )
D
练习3
结论
做匀速圆周运动的物体,其加速度的方向时刻指向圆心,这个加速度叫向心加速度
思考:是不是由此可以得出结论:“任何做匀速圆周运动的物体的加速度都指向圆心”?
暂时不能,因为上面只研究了有限的实例.还难以得出一般性的结论,需要数学上的论证来支持这一观点。
然而,这样的研究十分有益,因为它强烈地向我们提示了
问题的答案,给我们指出了方向.
思考
加速度的定义式是什么?
a
=
Δt
Δv
a
的方向与ΔV的方向相同
关键是如何确定ΔV
的方向?
速度的变化量ΔV
二、理论探究向心加速度的方向
结论:当△t→0时,△v与VA垂直(与半径平行),指向圆心,即做匀速圆周运动的物体,其瞬时加速度的方向指向圆心.
说明:并不是圆周运动的物体加速度都一定指向圆心,做变速圆周运动的物体(如洗衣机开机时和关机时洗衣筒的运动、电扇开和关时的运动),其合加速度不指向圆心,但有向心加速度这一分量,到后面我们会详细讨论。
?
直线运动的速度的变化量:
·
v1
v2
Δv
·
v1
v2
Δv
知识复习
作法:从同一点作出物体在一段时间的始末两个速度矢量v1和v2,从初速度v1的末端指向末速度v2的末端所作的矢量就是速度的变化量△v
。
?任意曲线运动中的速度的变化量:
v2
v1
v2
v1
Δv
v1
v2
Δv
由减数的末端指向
被减数的末端
首尾相连,由首指向尾
换个角度看这个等式
ΔV
=
V2-V1
ΔV
+
V1=V2
?
O
A
B
vA
vB
v
Δt
ΔV∕Δt表示平均加速度
当Δt→0时,此时ΔV∕Δt
表示
瞬时加速度
vA
r
(5)△V与圆的半径平行吗?
在什么条件下,△V的方向与圆的半径平行?
(1)在A、B两点画速度矢量vA和vB时,
要注意速度的方向与半径垂直。
(2)将VA的起点移到B点时要注意是平移
(3)如何画出质点由A点运动到B点时速度
的变化量△V?
(4)△v/△t表示的意义是什么?
ΔV
=
VB-VA
?匀速圆周运动的速度变化量
设质点做半径为r的匀速圆周运动,经过Δt从A运动到B
A
B
O
Δv
O
A
B
?匀速圆周运动的速度变化量
VA
VA
VB
VA
VB
Δv
Δv
思考:当Δt→0时,这个ΔV的方向是怎样的呢?
5
向心加速度
回顾:牛顿第一定律
牛顿第二定律
做圆周运动的物体是否一定受力?
那么做匀速圆周运动的物体所受合外力方向有什么特点?
如果物体不受力
做匀速直线运动或静止
做圆周运动的物体
变速曲线运动
根据牛顿第二定律(同样适用于曲线运动),即合外力一定不为零。
一定存在加速度
速度方向一定改变
地球受到什么力的作用?
这个力可能沿什么方向?
讨论
应该受到指向太阳的引力作用
因此,根据牛二(力与加速度具有同向性),地球的加速度的方向指向太阳
感知加速度的方向
V
F
F
F
V
V
结论:做匀速圆周运动的卫星,合外力方向
指向圆心(地心),与速度V垂直
卫星绕地球(行星)的运动
小球受到几个力的作用?
这几个力的合力沿什么方向?
小球受到重力、支持力和绳子的拉力三个力的作用,其合力即为绳子的拉力,其方向指向圆心
G
N
F拉
因此,小球的加速度的方向指向圆心
结论
做匀速圆周运动的物体,其加速度的方向时刻指向圆心,这个加速度叫向心加速度
O
B
A
vA
vB
vA
Δv
vA、vB、△v
组成的矢量三角形与ΔABO相似
∴
=
AB
Δv
v
r
∴
Δv
=
AB
v
r
∴
an
=
=
·
AB
v
r
Δv
Δt
Δt
当△t极小时,AB=AB=Δs
∴
=
=
=
v
AB
Δs
Δt
Δt
AB
Δt
∴
an
=
·
v
=
v
r
v2
r
Δ
θ
Δ
θ
推导过程:
向心加速度的大小
an
=
rω2
思考:
从公式
看,向心加速度与半径成反比;从公式
看,向心加速度与半径成正比;这两个结论是否矛盾?
an
=
v2
r
an
=
rω2
v不变时,an与r
成反比
ω不变时,an与r
成正比
an
=
vω
an
=
r
4π2
T
2
an
=
4π2
f
2r
=4π2
n2r
1、定义:
做匀速圆周运动的物体,
加速度始终
指向圆心,这个瞬时加速度就叫向心加速度。
3、物理意义:描述线速度的方向变化的快慢;
只改变线速度方向,不改变其大小
4、方向:
总是指向圆心,时刻变化,
是一个变加速度;
5、匀速圆周运动性质:变加速曲线运动;
四、匀速圆周运动的向心加速度
2、大小:
an
=
rω2
an
=
v2
r
谢谢!
五、变速圆周运动的加速度
竖直平面内的圆周运动一般是变速圆周运动(如重物在细绳/轻杆的作用下做圆周运动),运动的速度大小和方向在不断发生变化,运动过程复杂,合外力不仅要改变运动方向,还要改变速度大小。
练习1
如图所示,半径为R的圆盘绕过圆心的竖直轴OO′匀速转动,在距轴为r处有一竖直杆,杆上用长为L的细线悬挂一小球.当圆盘以角速度ω匀速转动时,小球也以同样的角速度做匀速圆周运动,这时细线与竖直方向的夹角为θ,则小球的向心加速度大小为(
)
A.
B.
C.
D.
D
如图所示,一个皮带传动减速装置,轮A和轮B共轴固定在一起组成一个塔形轮.各轮半径之比RA∶RB∶RC∶RD=2∶1∶1∶2,则运转过程中,轮C边缘上一点和轮D边缘上一点的线速度之比为__________,角速度之比为__________向心加速度之比为__________.
练习2
答案:
2∶1
4∶1
8∶1
如图所示,细绳的一端固定,另一端系一小球,让小球在竖直面内做圆周运动,关于小球运动到P点时的加速度方向,下列图中可能的是( )
D
练习3
结论
做匀速圆周运动的物体,其加速度的方向时刻指向圆心,这个加速度叫向心加速度
思考:是不是由此可以得出结论:“任何做匀速圆周运动的物体的加速度都指向圆心”?
暂时不能,因为上面只研究了有限的实例.还难以得出一般性的结论,需要数学上的论证来支持这一观点。
然而,这样的研究十分有益,因为它强烈地向我们提示了
问题的答案,给我们指出了方向.
思考
加速度的定义式是什么?
a
=
Δt
Δv
a
的方向与ΔV的方向相同
关键是如何确定ΔV
的方向?
速度的变化量ΔV
二、理论探究向心加速度的方向
结论:当△t→0时,△v与VA垂直(与半径平行),指向圆心,即做匀速圆周运动的物体,其瞬时加速度的方向指向圆心.
说明:并不是圆周运动的物体加速度都一定指向圆心,做变速圆周运动的物体(如洗衣机开机时和关机时洗衣筒的运动、电扇开和关时的运动),其合加速度不指向圆心,但有向心加速度这一分量,到后面我们会详细讨论。
?
直线运动的速度的变化量:
·
v1
v2
Δv
·
v1
v2
Δv
知识复习
作法:从同一点作出物体在一段时间的始末两个速度矢量v1和v2,从初速度v1的末端指向末速度v2的末端所作的矢量就是速度的变化量△v
。
?任意曲线运动中的速度的变化量:
v2
v1
v2
v1
Δv
v1
v2
Δv
由减数的末端指向
被减数的末端
首尾相连,由首指向尾
换个角度看这个等式
ΔV
=
V2-V1
ΔV
+
V1=V2
?
O
A
B
vA
vB
v
Δt
ΔV∕Δt表示平均加速度
当Δt→0时,此时ΔV∕Δt
表示
瞬时加速度
vA
r
(5)△V与圆的半径平行吗?
在什么条件下,△V的方向与圆的半径平行?
(1)在A、B两点画速度矢量vA和vB时,
要注意速度的方向与半径垂直。
(2)将VA的起点移到B点时要注意是平移
(3)如何画出质点由A点运动到B点时速度
的变化量△V?
(4)△v/△t表示的意义是什么?
ΔV
=
VB-VA
?匀速圆周运动的速度变化量
设质点做半径为r的匀速圆周运动,经过Δt从A运动到B
A
B
O
Δv
O
A
B
?匀速圆周运动的速度变化量
VA
VA
VB
VA
VB
Δv
Δv
思考:当Δt→0时,这个ΔV的方向是怎样的呢?
