探索勾股定理1.1

(共16张PPT)
北京欢迎您！
观看动画
请大家观察右图，我国科学家曾向太空发射如右图所示的图形试图与外星人沟通。2002年在北京召开的国际数学家大会上也采用此图作为会标。它为什么有如此大的魅力呢？它蕴含着怎样迷人的奥妙呢？这节课我们大家一起来探索这个问题。
探索勾股定理
学习目标（1分钟）
1.掌握直角三角形三边之间的关系：勾股定理，并会用字母表示
2.会采用数格子和割补的方法探索勾股定理
3.会运用勾股定理解决简单的计算问题
自学指导1：（2分钟）
1、自学课本P2－P4做一做完，完成下列问题：
2、解决做一做中的三个问题。
3、在做一做的（2）中，你是如何求每一个正 方形的面积的？与同学交流？。
学生自学，教师巡视（5分钟）
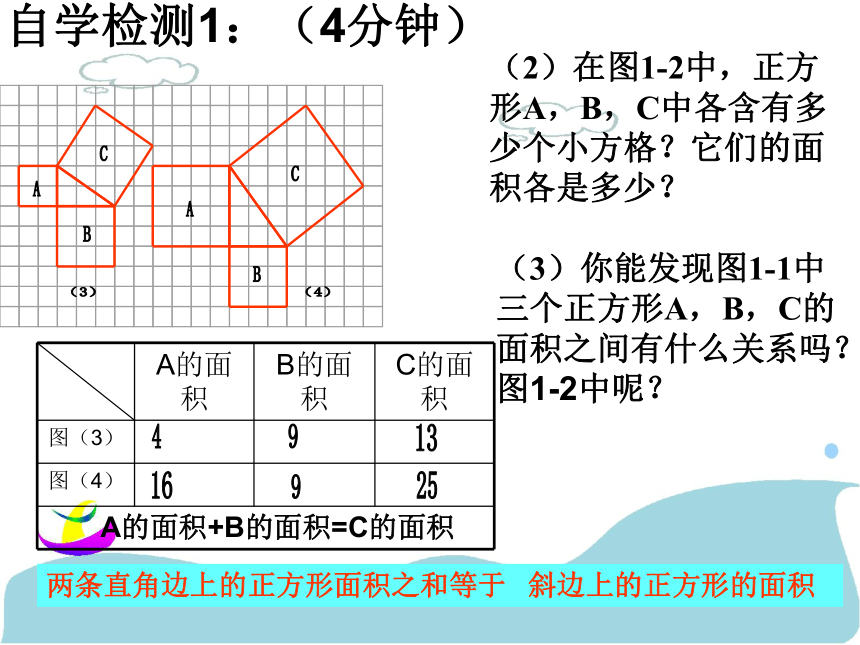
（2）在图1-2中，正方形A，B，C中各含有多少个小方格？它们的面积各是多少？
（3）你能发现图1-1中三个正方形A，B，C的面积之间有什么关系吗？图1-2中呢？
两条直角边上的正方形面积之和等于 斜边上的正方形的面积
















































































































































































































































A的面积 B的面积 C的面积
图（3）
图（4）
自学检测1：（4分钟）
A的面积+B的面积=C的面积
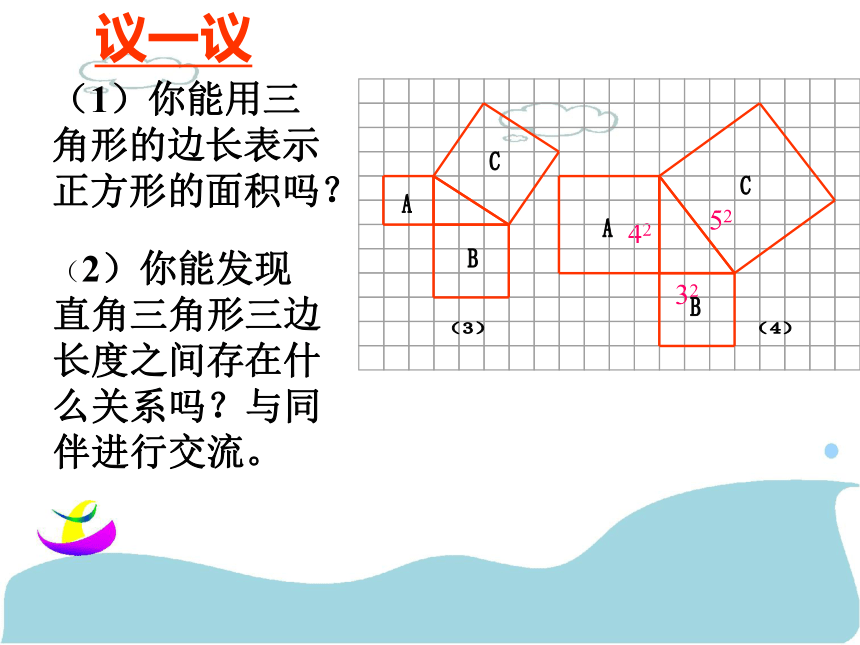
（1）你能用三角形的边长表示正方形的面积吗？
（2）你能发现直角三角形三边长度之间存在什么关系吗？与同伴进行交流。
议一议
42
c2
















































































































































































































































52
32
自学指导2（４分钟）
1.P4勾股定理是怎么叙述的，字母表
达式是如何表示的？
2.完成P4的想一想
3 ．Ｐ５的Ｔ１，Ｔ２　
１．勾股定理是怎么叙述的？
如果直角三角形两直角边分别为a、b,斜边为c，那么
直角三角形两直角边的平方和等于斜边的平方。
a
b
c
自学检测2（4分钟）
２．Ｐ４的想一想
３．Ｐ４的想一想 　　Ｐ５１．２题
　　　
　找同学到黑板演示或者放在投影仪展示
学生讨论，更正，教师点拨（５分钟）
当堂训练
3．Ｐ７的１，２,３,４题
1、在RtΔABC中，∠C＝90°，则三边之间满足_______________。
2、在ΔABC中，∠A＝90°，三边　　　　分别为a、b、c，且b＝3，c＝4，则a＝______。
变式题：
1.已知直角三角形的两条直角边为6cm和8cm, 则斜边上的高是　　　　。
2..求斜边长17厘米、一条直角边长15厘米的直角三角形的面积.
3.一高为18米的电线杆被大风吹断，已知落地点和电线杆的底部距离为12米，求折断点到电线杆的底部距离。（仿照想一想完成本题）
1。(1)某养殖厂有一个长2米、宽1.5米的矩形栅栏，现
在要在相对角的顶点间加固一条木板，则木板的长 应取——米.
(2)有两艘渔船同时离开某港口去捕鱼，其中一艘以 16海里/时的速度向东南方向航行，另一艘以12海里/ 时的速度向东北方向航行，它们离开港口一个半小时后相距——海里.
(3)如图1：隔湖有两点A、B，为了测得A、B两点间的距离，从与AB方向成直角的BC方向上任取一点C，若测得CA=50 m,CB=40 m，那么A、B两点间的距离是_________.
图1
思考题
2.已知一个等腰三角形的底边和腰的长分别为12 cm和10 cm，求这个三角形的面积.
3.在△ABC中，∠C=90°,AC=2.1 cm,BC=2.8 cm
（1）求这个三角形的斜边AB的长和斜边上的高CD的长.
（2）求斜边被分成的两部分AD和BD的长.
4.如图3，已知长方形ABCD中AB=8 cm,BC=10 cm,在边CD上取一点E，将△ADE折叠使点D恰好落在BC边上的点F，求CE的长.
课堂小结：
1、你能准确理解勾股定理吗？
在R t △ABC中，若∠C＝90°，三边分别为a、b、c，则___________。
2、能正确运用勾股定理进行直角三角形的有关边的计算吗？
作业
准备4张全等的直角三角形纸片
预习验证勾股定理的方法
a
b
c