人教版九年级上册数学 24.2.2 直线和圆的位置关系 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版九年级上册数学 24.2.2 直线和圆的位置关系 同步练习(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 230.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-13 22:04:08 | ||
图片预览


文档简介
24.2.2
直线和圆的位置关系
同步练习
一.选择题
1.如图,AB是⊙O的切线,A为切点,连接OA,OB,若∠B=20°,则∠AOB的度数为( )
A.40°
B.50°
C.60°
D.70°
2.如图,△ABC内接于圆,∠ACB=90°,过点C的切线交AB的延长线于点P,∠P=28°.则∠CAB=( )
A.62°
B.31°
C.28°
D.56°
3.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O的位置关系是( )
A.相离
B.相交
C.相切
D.不确定
4.《九章算术》中有一题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是( )
A.6步
B.7步
C.8步
D.9步
5.已知三角形的周长为12,面积为6,则该三角形内切圆的半径为( )
A.4
B.3
C.2
D.1
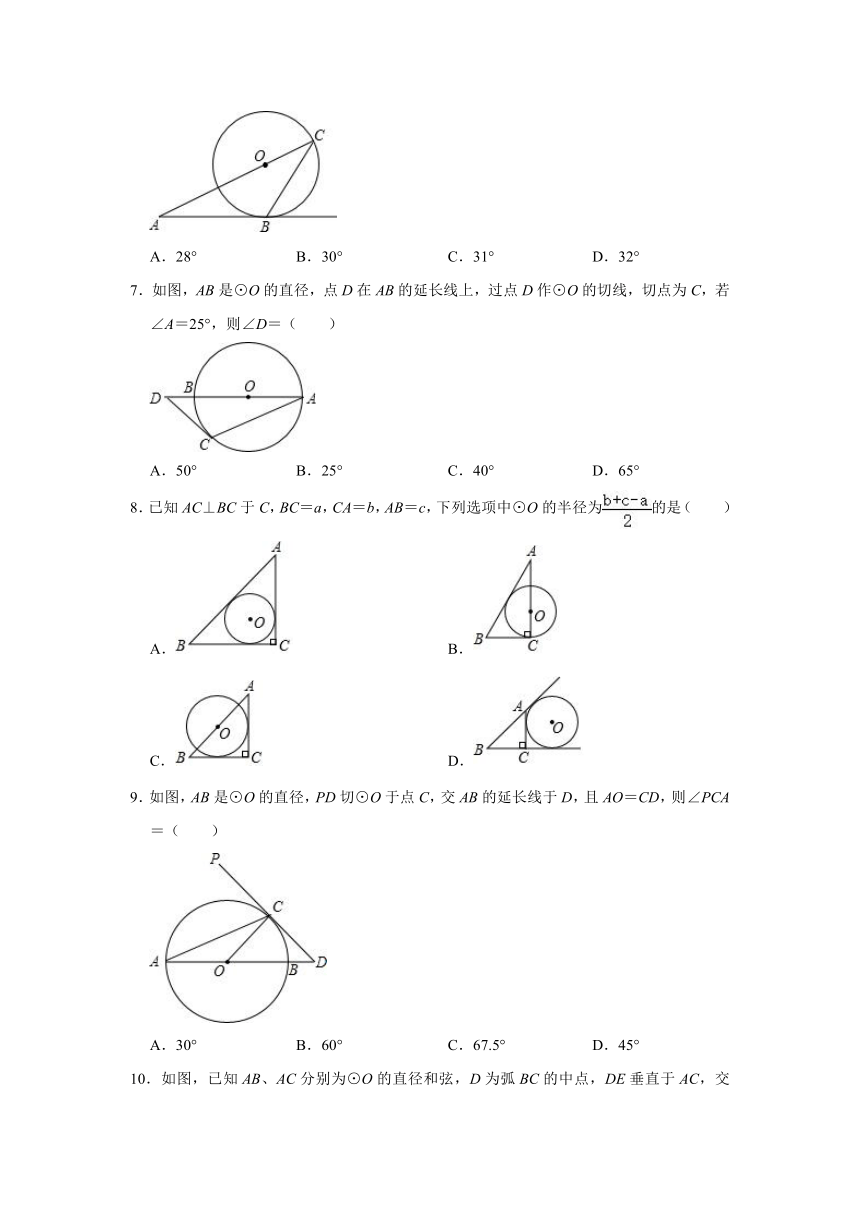
6.如图,从⊙O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=28°,则∠ACB的度数是( )
A.28°
B.30°
C.31°
D.32°
7.如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D=( )
A.50°
B.25°
C.40°
D.65°
8.已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为的是( )
A.
B.
C.
D.
9.如图,AB是⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且AO=CD,则∠PCA=( )
A.30°
B.60°
C.67.5°
D.45°
10.如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论正确的是( )
①DE是⊙O的切线;②直径AB长为20cm;③弦AC长为15cm;④C为弧AD的中点.
A.①②④
B.①③④
C.①②
D.②③
二.填空题
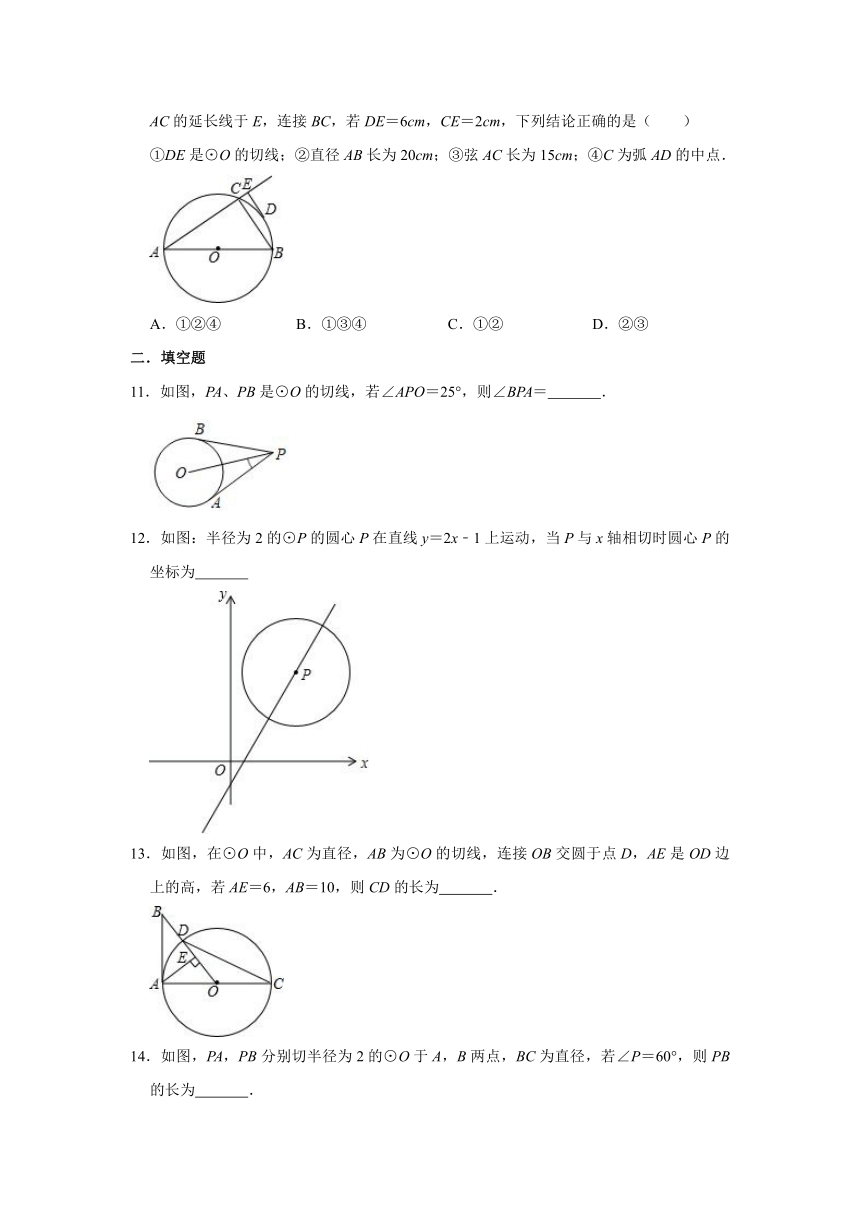
11.如图,PA、PB是⊙O的切线,若∠APO=25°,则∠BPA=
.
12.如图:半径为2的⊙P的圆心P在直线y=2x﹣1上运动,当P与x轴相切时圆心P的坐标为
13.如图,在⊙O中,AC为直径,AB为⊙O的切线,连接OB交圆于点D,AE是OD边上的高,若AE=6,AB=10,则CD的长为
.
14.如图,PA,PB分别切半径为2的⊙O于A,B两点,BC为直径,若∠P=60°,则PB的长为
.
15.如图,AB是⊙O的直径,CD与⊙O相切于点C,∠BCD=25°,∠ABC=
°.
三.解答题
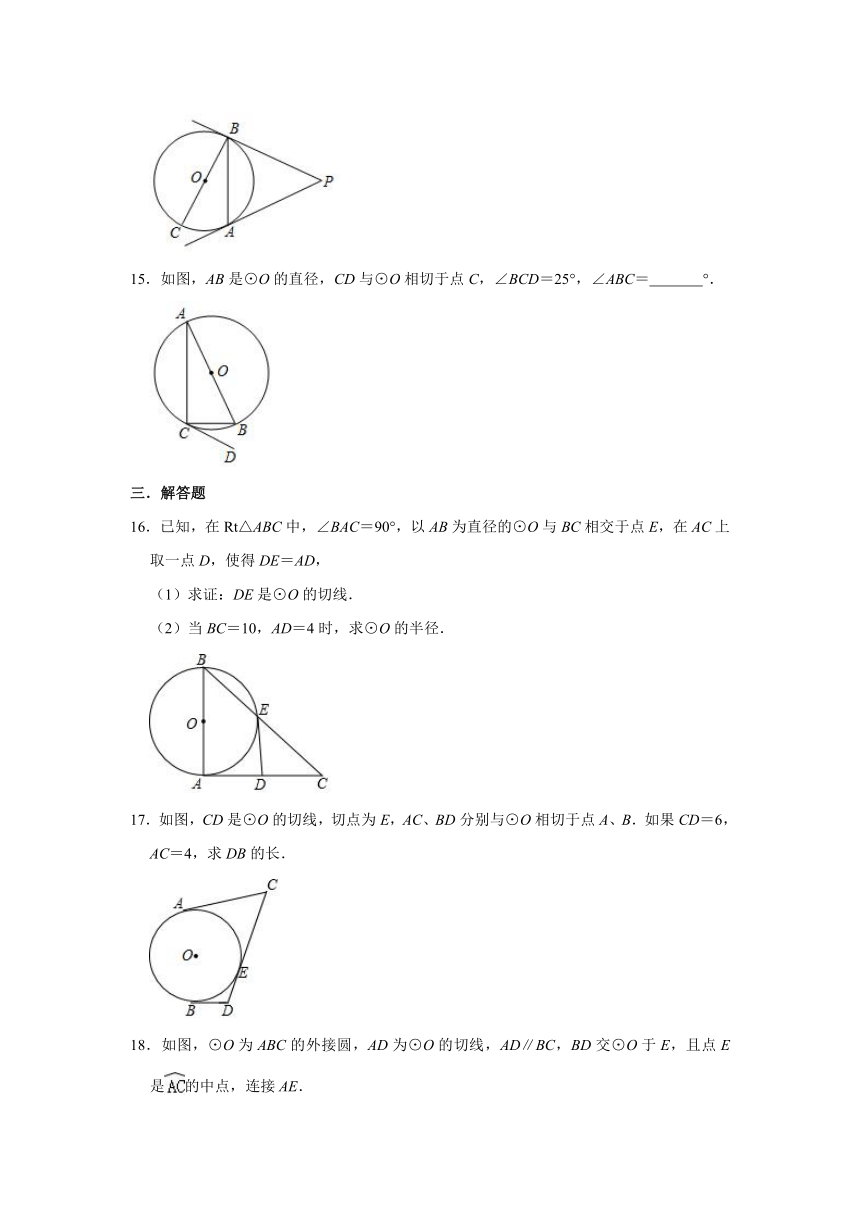
16.已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,
(1)求证:DE是⊙O的切线.
(2)当BC=10,AD=4时,求⊙O的半径.
17.如图,CD是⊙O的切线,切点为E,AC、BD分别与⊙O相切于点A、B.如果CD=6,AC=4,求DB的长.
18.如图,⊙O为ABC的外接圆,AD为⊙O的切线,AD∥BC,BD交⊙O于E,且点E是的中点,连接AE.
(1)求证:AE平分∠DAC;
(2)若AD=40,BC=48,求⊙O的半径长及AE的长.
参考答案
1.解:∵AB是⊙O的切线,A为切点,
∴∠A=90°,
∵∠B=20°,
∴∠AOB=90°﹣20°=70°,
故选:D.
2.解:连接OC,如图,
∵PC为切线,
∴OC⊥PC,
∴∠PCO=90°,
∴∠POC=90°﹣∠P=90°﹣28°=62°,
∵OA=OC,
∴∠A=∠OCA,
而∠POC=∠A+∠OCA,
∴∠A=×62°=31°.
故选:B.
3.解:∵d=3<半径=4,
∴直线与圆相交,
故选:B.
4.解:根据勾股定理得:斜边为,
则该直角三角形能容纳的圆形(内切圆)半径r==3,
即直径为6步,
故选:A.
5.解:设这个三角形的内切圆半径是r,
∵三角形周长为12,面积为6,
∴×12r=6,
解得r=1.
故选:D.
6.解:连接OB,如图,
∵AB为切线,
∴OB⊥AB,
∴∠ABO=90°,
∴∠AOB=90°﹣∠A=90°﹣28°=62°,
∴∠ACB=∠AOB=31°.
故选:C.
7.解:如图:连接OC
∵OA=OC,
∴∠A=∠OCA=25°,
∴∠DOC=2∠A=50°,
∵过点D作⊙O的切线,切点为C,
∴∠OCD=90°,
∴∠D=40°.
故选:C.
8.解:A、设圆的半径是x,圆切AC于E,切BC于D,切AB于F,如图(1),
同样得到正方形OECD,AE=AF,BD=BF,则a﹣x+b﹣x=c,
∴x=,
故本选项错误;
B、设圆切AB于F,圆的半径是y,连接OF,如图(2),
则△BCA∽△OFA,,
,
,
故本选项错误;
C、连接OE、OD,
∵AC、BC分别切圆O于E、D,
∴∠OEC=∠ODC=∠C=90°,
∵OE=OD,
∴四边形OECD是正方形,
∴OE=EC=CD=OD,
设圆O的半径是r,
∵OE∥BC,
∴∠AOE=∠B,
∵∠AEO=∠ODB,
∴△ODB∽△AEO,
,
,
解得:r=,
故本选项错误;
D、从上至下三个切点依次为D,E,F;并设圆的半径为x;
∵BD=BF,
∴AD=BD﹣BA=BF﹣BA=a+x﹣c;
又∵b﹣x=AE=AD=a+x﹣c;
所以x=,
故本选项正确.
故选:D.
9.解:∵PD切⊙O于点C,
∴∠OCD=90°,
∵AO=CD,
∴OC=DC,
∴∠COD=∠D=45°,
∵AO=CO,
∴∠A=∠ACO=22.5°,
∴∠PCA=90°﹣22.5°=67.5°.
故选:C.
10.解:如图,连接OD,交BC于点F,连接OC,
∵D为弧BC的中点,
∴OD⊥BC,且CF=BF,
又∵AB为⊙O的直径,DE⊥AE,
∴∠BCE=∠DEC=∠CFD=90°,
∴四边形CEDF为矩形,
∴OD⊥DE,
∴DE为⊙O的切线,
故①正确;
∴DF=CE=2cm,CF=DE=6cm,
∴BC=2CF=12cm,
设半径为rcm,则OF=(r﹣2)cm,
在Rt△OCF中,由勾股定理可得OC2=OF2+CF2,即r2=(r﹣2)2+62,解得r=10cm,
∴AB=20cm,
故②正确;
在Rt△ABC中,BC=12cm,AB=20cm,
∴AC===16(cm),
故③不正确;
若C为弧AD的中点,则AC=CD,
在Rt△CDE中,CE=2cm,DE=6cm,由勾股定理可求得CD=2cm≠AC,
故④不正确;
综上可知正确的为①②,
故选:C.
11.解:∵PA、PB是⊙O的切线,
∴∠BPO=∠APO=25°,
∴∠BPA=50°,
故答案为:50°.
12.解:设P点坐标为(t,2t﹣1),
∵⊙P与x轴相切,
∴|2t﹣1|=2,解得t=或t=﹣,
∴点P的坐标为(﹣,﹣2)或(,2).
故答案为:(﹣,﹣2)或(,2).
13.解:连结AD,如图,
∵AE是OD边上的高,
∴∠AEB=90°,
在Rt△ABE中,∵AB=10,AE=6,
∴BE==8,
∵AB为⊙O的切线,
∴OA⊥AB,
∵∠ABE=∠OBA,
∴Rt△BAE∽Rt△BOA,
∴=,即=,解得OB=,
在Rt△ABO中,OA===,
在Rt△AOE中,OE==,
∴DE=OD﹣OE=﹣=3,
在Rt△ADE中,AD==3,
∵AC为直径,
∴∠ADC=90°,
在Rt△ADC中,CD===6.
故答案为6.
14.解:如图所示:连接AC,
∵PA,PB是切线,
∴PA=PB.
又∵∠P=60°,
∴AB=PB,∠ABP=60°,
又CB⊥PB,
∴∠ABC=30°.
∵BC是直径,BC=4,
∴∠BAC=90°.
∴AB=BC?cos30°=4×=2.
∴PB=2;
故答案为:2.
15.解:连接OC,如图,
∵CD切⊙O于点C,
∴OC⊥CD,
∴∠OCD=90°,
∴∠OCB=90°﹣∠BCD=90°﹣25°=65°,
∵OB=OC,
∴∠B=∠OCB=65°.
故答案为:65.
16.(1)证明:连接OE、OD,
在△AOD和△EOD中,
,
∴△AOD≌△EOD(SSS),
∴∠OED=∠BAC=90°,
∴DE是⊙O的切线;
(2)解:∵△AOD≌△EOD,
∴∠AOD=∠EOD,
∵OB=OE,
∴∠B=∠OEB,
∵∠AOE=∠B+∠OEB,
∴∠BEO=∠EOD,
∴OD∥BC,又AO=BO,
∴OD=BC=5,
由勾股定理得,AO==3,
则⊙O的半径为3.
17.解:∵CD切⊙O
点E,AC切切⊙O
点A.
∴CE=AC=4,
∴ED=CD﹣CE=2,
∵CD切⊙O
点E,BD切⊙O
点B.
∴BD=ED=2.
18.解:(1)∵点E是的中点,
∴∠ABE=∠CBE,
∵AD为⊙O的切线,
∴∠ABE=∠DAE,
∵∠EAC=∠CBE,
∴∠DAE=∠CAE,
∴AE平分∠DAC;
(2)如图,连接OA、OE,延长AO交BC于M.
∵AD是切线,
∴OA⊥AD,
∵AD∥BC,
∴AM⊥BC,
∴BM=CM=24,
∴AB=AC,
∵AB=40,
∴AM===32,设半径为r,
在Rt△COM中,∵OC2=OM2+CM2,
∴x2=(32﹣x)2+242,
∴x=25,
∴OA=25,
∵=,
∴EO⊥AC,
在Rt△AON中,∵OA=25,AN=20,
∴ON==15,EN=OE﹣ON=10,
在Rt△ANE中,
AE===10.
直线和圆的位置关系
同步练习
一.选择题
1.如图,AB是⊙O的切线,A为切点,连接OA,OB,若∠B=20°,则∠AOB的度数为( )
A.40°
B.50°
C.60°
D.70°
2.如图,△ABC内接于圆,∠ACB=90°,过点C的切线交AB的延长线于点P,∠P=28°.则∠CAB=( )
A.62°
B.31°
C.28°
D.56°
3.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O的位置关系是( )
A.相离
B.相交
C.相切
D.不确定
4.《九章算术》中有一题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是( )
A.6步
B.7步
C.8步
D.9步
5.已知三角形的周长为12,面积为6,则该三角形内切圆的半径为( )
A.4
B.3
C.2
D.1
6.如图,从⊙O外一点A引圆的切线AB,切点为B,连接AO并延长交圆于点C,连接BC.若∠A=28°,则∠ACB的度数是( )
A.28°
B.30°
C.31°
D.32°
7.如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,则∠D=( )
A.50°
B.25°
C.40°
D.65°
8.已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为的是( )
A.
B.
C.
D.
9.如图,AB是⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且AO=CD,则∠PCA=( )
A.30°
B.60°
C.67.5°
D.45°
10.如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论正确的是( )
①DE是⊙O的切线;②直径AB长为20cm;③弦AC长为15cm;④C为弧AD的中点.
A.①②④
B.①③④
C.①②
D.②③
二.填空题
11.如图,PA、PB是⊙O的切线,若∠APO=25°,则∠BPA=
.
12.如图:半径为2的⊙P的圆心P在直线y=2x﹣1上运动,当P与x轴相切时圆心P的坐标为
13.如图,在⊙O中,AC为直径,AB为⊙O的切线,连接OB交圆于点D,AE是OD边上的高,若AE=6,AB=10,则CD的长为
.
14.如图,PA,PB分别切半径为2的⊙O于A,B两点,BC为直径,若∠P=60°,则PB的长为
.
15.如图,AB是⊙O的直径,CD与⊙O相切于点C,∠BCD=25°,∠ABC=
°.
三.解答题
16.已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,
(1)求证:DE是⊙O的切线.
(2)当BC=10,AD=4时,求⊙O的半径.
17.如图,CD是⊙O的切线,切点为E,AC、BD分别与⊙O相切于点A、B.如果CD=6,AC=4,求DB的长.
18.如图,⊙O为ABC的外接圆,AD为⊙O的切线,AD∥BC,BD交⊙O于E,且点E是的中点,连接AE.
(1)求证:AE平分∠DAC;
(2)若AD=40,BC=48,求⊙O的半径长及AE的长.
参考答案
1.解:∵AB是⊙O的切线,A为切点,
∴∠A=90°,
∵∠B=20°,
∴∠AOB=90°﹣20°=70°,
故选:D.
2.解:连接OC,如图,
∵PC为切线,
∴OC⊥PC,
∴∠PCO=90°,
∴∠POC=90°﹣∠P=90°﹣28°=62°,
∵OA=OC,
∴∠A=∠OCA,
而∠POC=∠A+∠OCA,
∴∠A=×62°=31°.
故选:B.
3.解:∵d=3<半径=4,
∴直线与圆相交,
故选:B.
4.解:根据勾股定理得:斜边为,
则该直角三角形能容纳的圆形(内切圆)半径r==3,
即直径为6步,
故选:A.
5.解:设这个三角形的内切圆半径是r,
∵三角形周长为12,面积为6,
∴×12r=6,
解得r=1.
故选:D.
6.解:连接OB,如图,
∵AB为切线,
∴OB⊥AB,
∴∠ABO=90°,
∴∠AOB=90°﹣∠A=90°﹣28°=62°,
∴∠ACB=∠AOB=31°.
故选:C.
7.解:如图:连接OC
∵OA=OC,
∴∠A=∠OCA=25°,
∴∠DOC=2∠A=50°,
∵过点D作⊙O的切线,切点为C,
∴∠OCD=90°,
∴∠D=40°.
故选:C.
8.解:A、设圆的半径是x,圆切AC于E,切BC于D,切AB于F,如图(1),
同样得到正方形OECD,AE=AF,BD=BF,则a﹣x+b﹣x=c,
∴x=,
故本选项错误;
B、设圆切AB于F,圆的半径是y,连接OF,如图(2),
则△BCA∽△OFA,,
,
,
故本选项错误;
C、连接OE、OD,
∵AC、BC分别切圆O于E、D,
∴∠OEC=∠ODC=∠C=90°,
∵OE=OD,
∴四边形OECD是正方形,
∴OE=EC=CD=OD,
设圆O的半径是r,
∵OE∥BC,
∴∠AOE=∠B,
∵∠AEO=∠ODB,
∴△ODB∽△AEO,
,
,
解得:r=,
故本选项错误;
D、从上至下三个切点依次为D,E,F;并设圆的半径为x;
∵BD=BF,
∴AD=BD﹣BA=BF﹣BA=a+x﹣c;
又∵b﹣x=AE=AD=a+x﹣c;
所以x=,
故本选项正确.
故选:D.
9.解:∵PD切⊙O于点C,
∴∠OCD=90°,
∵AO=CD,
∴OC=DC,
∴∠COD=∠D=45°,
∵AO=CO,
∴∠A=∠ACO=22.5°,
∴∠PCA=90°﹣22.5°=67.5°.
故选:C.
10.解:如图,连接OD,交BC于点F,连接OC,
∵D为弧BC的中点,
∴OD⊥BC,且CF=BF,
又∵AB为⊙O的直径,DE⊥AE,
∴∠BCE=∠DEC=∠CFD=90°,
∴四边形CEDF为矩形,
∴OD⊥DE,
∴DE为⊙O的切线,
故①正确;
∴DF=CE=2cm,CF=DE=6cm,
∴BC=2CF=12cm,
设半径为rcm,则OF=(r﹣2)cm,
在Rt△OCF中,由勾股定理可得OC2=OF2+CF2,即r2=(r﹣2)2+62,解得r=10cm,
∴AB=20cm,
故②正确;
在Rt△ABC中,BC=12cm,AB=20cm,
∴AC===16(cm),
故③不正确;
若C为弧AD的中点,则AC=CD,
在Rt△CDE中,CE=2cm,DE=6cm,由勾股定理可求得CD=2cm≠AC,
故④不正确;
综上可知正确的为①②,
故选:C.
11.解:∵PA、PB是⊙O的切线,
∴∠BPO=∠APO=25°,
∴∠BPA=50°,
故答案为:50°.
12.解:设P点坐标为(t,2t﹣1),
∵⊙P与x轴相切,
∴|2t﹣1|=2,解得t=或t=﹣,
∴点P的坐标为(﹣,﹣2)或(,2).
故答案为:(﹣,﹣2)或(,2).
13.解:连结AD,如图,
∵AE是OD边上的高,
∴∠AEB=90°,
在Rt△ABE中,∵AB=10,AE=6,
∴BE==8,
∵AB为⊙O的切线,
∴OA⊥AB,
∵∠ABE=∠OBA,
∴Rt△BAE∽Rt△BOA,
∴=,即=,解得OB=,
在Rt△ABO中,OA===,
在Rt△AOE中,OE==,
∴DE=OD﹣OE=﹣=3,
在Rt△ADE中,AD==3,
∵AC为直径,
∴∠ADC=90°,
在Rt△ADC中,CD===6.
故答案为6.
14.解:如图所示:连接AC,
∵PA,PB是切线,
∴PA=PB.
又∵∠P=60°,
∴AB=PB,∠ABP=60°,
又CB⊥PB,
∴∠ABC=30°.
∵BC是直径,BC=4,
∴∠BAC=90°.
∴AB=BC?cos30°=4×=2.
∴PB=2;
故答案为:2.
15.解:连接OC,如图,
∵CD切⊙O于点C,
∴OC⊥CD,
∴∠OCD=90°,
∴∠OCB=90°﹣∠BCD=90°﹣25°=65°,
∵OB=OC,
∴∠B=∠OCB=65°.
故答案为:65.
16.(1)证明:连接OE、OD,
在△AOD和△EOD中,
,
∴△AOD≌△EOD(SSS),
∴∠OED=∠BAC=90°,
∴DE是⊙O的切线;
(2)解:∵△AOD≌△EOD,
∴∠AOD=∠EOD,
∵OB=OE,
∴∠B=∠OEB,
∵∠AOE=∠B+∠OEB,
∴∠BEO=∠EOD,
∴OD∥BC,又AO=BO,
∴OD=BC=5,
由勾股定理得,AO==3,
则⊙O的半径为3.
17.解:∵CD切⊙O
点E,AC切切⊙O
点A.
∴CE=AC=4,
∴ED=CD﹣CE=2,
∵CD切⊙O
点E,BD切⊙O
点B.
∴BD=ED=2.
18.解:(1)∵点E是的中点,
∴∠ABE=∠CBE,
∵AD为⊙O的切线,
∴∠ABE=∠DAE,
∵∠EAC=∠CBE,
∴∠DAE=∠CAE,
∴AE平分∠DAC;
(2)如图,连接OA、OE,延长AO交BC于M.
∵AD是切线,
∴OA⊥AD,
∵AD∥BC,
∴AM⊥BC,
∴BM=CM=24,
∴AB=AC,
∵AB=40,
∴AM===32,设半径为r,
在Rt△COM中,∵OC2=OM2+CM2,
∴x2=(32﹣x)2+242,
∴x=25,
∴OA=25,
∵=,
∴EO⊥AC,
在Rt△AON中,∵OA=25,AN=20,
∴ON==15,EN=OE﹣ON=10,
在Rt△ANE中,
AE===10.
同课章节目录
