华东师大版九年级数学上学期《第24章 解直角三角形》 单元同步卷(word版含答案)
文档属性
| 名称 | 华东师大版九年级数学上学期《第24章 解直角三角形》 单元同步卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 143.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-13 22:35:50 | ||
图片预览




文档简介
第24章
解直角三角形
一.选择题
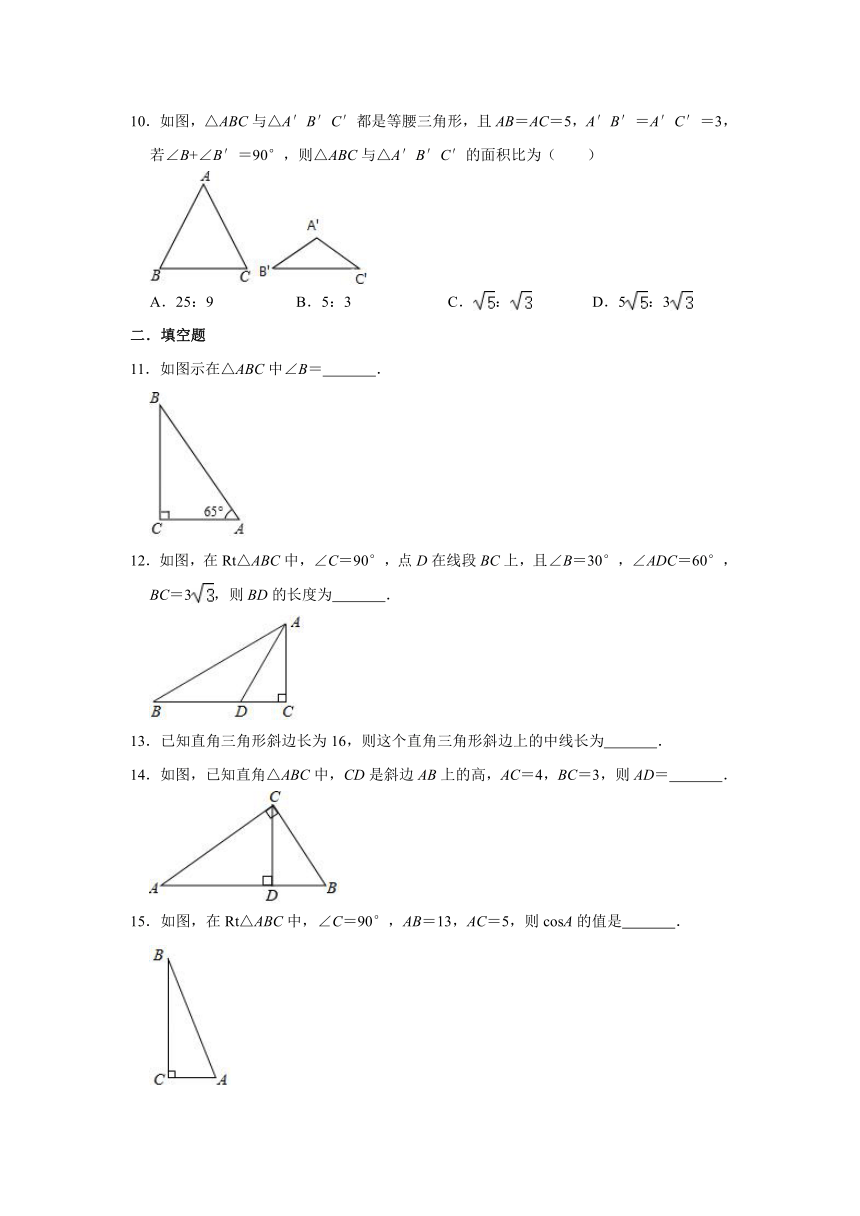
1.把Rt△ABC与Rt△CDE放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,若∠B=25°,∠D=58°,则∠BCE的度数是( )
A.83°
B.57°
C.54°
D.33°
2.在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是( )
A.BC=EC
B.EC=BE
C.BC=BE
D.AE=EC
3.如图,在平面直角坐标系中,Rt△OAB的斜边OA在第一象限,并与x轴的正半轴夹角为30°.C为OA的中点,BC=1,则点A的坐标为( )
A.(,)
B.(,1)
C.(2,1)
D.(2,)
4.△ABC中,AB=AC,∠BAC=120°,BC=2,D为BC的中点,AE=AB,则△EBD的面积为( )
A.
B.
C.
D.
5.如图,AB是⊙O的弦,点C是优弧AB上的动点(C不与A、B重合),CH⊥AB,垂足为H,点M是BC的中点.若⊙O的半径是3,则MH长的最大值是( )
A.3
B.4
C.5
D.6
6.在Rt△ABC中,AD是斜边BC上的高线,若BD=2,BC=6,则AB=( )
A.
B.
C.
D.
7.在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )
A.
B.
C.
D.
8.如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
A.不变
B.增大
C.减小
D.先变大再变小
9.规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,cos(x+y)=cosxcosy﹣sinxsiny,给出以下四个结论:
(1)sin(﹣30°)=﹣;
(2)cos2x=cos2x﹣sin2x;
(3)cos(x﹣y)=cosxcosy+sinxsiny;
(4)cos15°=.
其中正确的结论的个数为( )
A.1个
B.2个
C.3个
D.4个
10.如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为( )
A.25:9
B.5:3
C.:
D.5:3
二.填空题
11.如图示在△ABC中∠B=
.
12.如图,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=3,则BD的长度为
.
13.已知直角三角形斜边长为16,则这个直角三角形斜边上的中线长为
.
14.如图,已知直角△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD=
.
15.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是
.
三.解答题
16.如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
17.如图,在平行四边形ABCD中,AE是BC边上的高,点F是DE的中点,AB与AG关于AE对称,AE与AF关于AG对称.
(1)求证:△AEF是等边三角形;
(2)若AB=2,求△AFD的面积.
18.如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.
(1)求证:EF=AC.
(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.
19.如图,在△ABC中,∠C=150°,AC=4,tanB=.
(1)求BC的长;
(2)利用此图形求tan15°的值(精确到0.1,参考数据:=1.4,=1.7,=2.2)
20.已知α为锐角,且,求的值.
参考答案
一.选择题
1.
B.
2.
C.
3.B.
4.
B.
5.
A.
6.
C.
7.
D.
8.
C.
9.
C.
10.
A.
二.填空题
11.
25°.
12.
2.
13.
8.
14..
15.
.
三.解答题
16.(1)证明:∵直角△ABC中,∠C=90°﹣∠A=30°.
∵CD=4t,AE=2t,
又∵在直角△CDF中,∠C=30°,
∴DF=CD=2t,
∴DF=AE;
解:(2)∵DF∥AB,DF=AE,
∴四边形AEFD是平行四边形,
当AD=AE时,四边形AEFD是菱形,
即60﹣4t=2t,
解得:t=10,
即当t=10时,?AEFD是菱形;
(3)当t=时△DEF是直角三角形(∠EDF=90°);
当t=12时,△DEF是直角三角形(∠DEF=90°).理由如下:
当∠EDF=90°时,DE∥BC.
∴∠ADE=∠C=30°
∴AD=2AE
∵CD=4t,
∴DF=2t=AE,
∴AD=4t,
∴4t+4t=60,
∴t=时,∠EDF=90°.
当∠DEF=90°时,DE⊥EF,
∵四边形AEFD是平行四边形,
∴AD∥EF,
∴DE⊥AD,
∴△ADE是直角三角形,∠ADE=90°,
∵∠A=60°,
∴∠DEA=30°,
∴AD=AE,
AD=AC﹣CD=60﹣4t,AE=DF=CD=2t,
∴60﹣4t=t,
解得t=12.
综上所述,当t=时△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°).
17.解:(1)∵AE是BC边上的高,
∴AE⊥BC,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AE⊥AD,即∠DAE=90°,
∵点F是DE的中点,即AF是Rt△ADE的中线,
∴AF=EF=DF,
∵AE与AF关于AG对称,
∴AE=AF,
则AE=AF=EF,
∴△AEF是等边三角形;
(2)记AG、EF交点为H,
∵△AEF是等边三角形,且AE与AF关于AG对称,
∴∠EAG=30°,AG⊥EF,
∵AB与AG关于AE对称,
∴∠BAE=∠GAE=30°,∠AEB=90°,
∵AB=2,
∴BE=1、DF=AF=AE=,
则EH=AE=、AH=,
∴S△ADF=××=.
18.(1)证明:∵CD=CB,点E为BD的中点,
∴CE⊥BD,
∵点F为AC的中点,
∴EF=AC;
(2)解:∵∠BAC=45°,CE⊥BD,
∴△AEC是等腰直角三角形,
∵点F为AC的中点,
∴EF垂直平分AC,
∴AM=CM,
∵CD=CM+DM=AM+DM,CD=CB,
∴BC=AM+DM.
19.解:(1)过A作AD⊥BC,交BC的延长线于点D,如图1所示:
在Rt△ADC中,AC=4,
∵∠C=150°,
∴∠ACD=30°,
∴AD=AC=2,
CD=AC?cos30°=4×=2,
在Rt△ABD中,tanB===,
∴BD=16,
∴BC=BD﹣CD=16﹣2;
(2)在BC边上取一点M,使得CM=AC,连接AM,如图2所示:
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,
tan15°=tan∠AMD====2﹣≈0.27≈0.3.
20.解:如图,设∠α为直角三角形的一个锐角,
∵cosα=,
∴设α的邻边为1k,斜边为3k,
由勾股定理,得α的对边为=2k,
∴tanα=2,sinα=,
故=2+
=2+3﹣2=3.
解直角三角形
一.选择题
1.把Rt△ABC与Rt△CDE放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,若∠B=25°,∠D=58°,则∠BCE的度数是( )
A.83°
B.57°
C.54°
D.33°
2.在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是( )
A.BC=EC
B.EC=BE
C.BC=BE
D.AE=EC
3.如图,在平面直角坐标系中,Rt△OAB的斜边OA在第一象限,并与x轴的正半轴夹角为30°.C为OA的中点,BC=1,则点A的坐标为( )
A.(,)
B.(,1)
C.(2,1)
D.(2,)
4.△ABC中,AB=AC,∠BAC=120°,BC=2,D为BC的中点,AE=AB,则△EBD的面积为( )
A.
B.
C.
D.
5.如图,AB是⊙O的弦,点C是优弧AB上的动点(C不与A、B重合),CH⊥AB,垂足为H,点M是BC的中点.若⊙O的半径是3,则MH长的最大值是( )
A.3
B.4
C.5
D.6
6.在Rt△ABC中,AD是斜边BC上的高线,若BD=2,BC=6,则AB=( )
A.
B.
C.
D.
7.在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )
A.
B.
C.
D.
8.如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
A.不变
B.增大
C.减小
D.先变大再变小
9.规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,cos(x+y)=cosxcosy﹣sinxsiny,给出以下四个结论:
(1)sin(﹣30°)=﹣;
(2)cos2x=cos2x﹣sin2x;
(3)cos(x﹣y)=cosxcosy+sinxsiny;
(4)cos15°=.
其中正确的结论的个数为( )
A.1个
B.2个
C.3个
D.4个
10.如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为( )
A.25:9
B.5:3
C.:
D.5:3
二.填空题
11.如图示在△ABC中∠B=
.
12.如图,在Rt△ABC中,∠C=90°,点D在线段BC上,且∠B=30°,∠ADC=60°,BC=3,则BD的长度为
.
13.已知直角三角形斜边长为16,则这个直角三角形斜边上的中线长为
.
14.如图,已知直角△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD=
.
15.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是
.
三.解答题
16.如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
17.如图,在平行四边形ABCD中,AE是BC边上的高,点F是DE的中点,AB与AG关于AE对称,AE与AF关于AG对称.
(1)求证:△AEF是等边三角形;
(2)若AB=2,求△AFD的面积.
18.如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.
(1)求证:EF=AC.
(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.
19.如图,在△ABC中,∠C=150°,AC=4,tanB=.
(1)求BC的长;
(2)利用此图形求tan15°的值(精确到0.1,参考数据:=1.4,=1.7,=2.2)
20.已知α为锐角,且,求的值.
参考答案
一.选择题
1.
B.
2.
C.
3.B.
4.
B.
5.
A.
6.
C.
7.
D.
8.
C.
9.
C.
10.
A.
二.填空题
11.
25°.
12.
2.
13.
8.
14..
15.
.
三.解答题
16.(1)证明:∵直角△ABC中,∠C=90°﹣∠A=30°.
∵CD=4t,AE=2t,
又∵在直角△CDF中,∠C=30°,
∴DF=CD=2t,
∴DF=AE;
解:(2)∵DF∥AB,DF=AE,
∴四边形AEFD是平行四边形,
当AD=AE时,四边形AEFD是菱形,
即60﹣4t=2t,
解得:t=10,
即当t=10时,?AEFD是菱形;
(3)当t=时△DEF是直角三角形(∠EDF=90°);
当t=12时,△DEF是直角三角形(∠DEF=90°).理由如下:
当∠EDF=90°时,DE∥BC.
∴∠ADE=∠C=30°
∴AD=2AE
∵CD=4t,
∴DF=2t=AE,
∴AD=4t,
∴4t+4t=60,
∴t=时,∠EDF=90°.
当∠DEF=90°时,DE⊥EF,
∵四边形AEFD是平行四边形,
∴AD∥EF,
∴DE⊥AD,
∴△ADE是直角三角形,∠ADE=90°,
∵∠A=60°,
∴∠DEA=30°,
∴AD=AE,
AD=AC﹣CD=60﹣4t,AE=DF=CD=2t,
∴60﹣4t=t,
解得t=12.
综上所述,当t=时△DEF是直角三角形(∠EDF=90°);当t=12时,△DEF是直角三角形(∠DEF=90°).
17.解:(1)∵AE是BC边上的高,
∴AE⊥BC,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AE⊥AD,即∠DAE=90°,
∵点F是DE的中点,即AF是Rt△ADE的中线,
∴AF=EF=DF,
∵AE与AF关于AG对称,
∴AE=AF,
则AE=AF=EF,
∴△AEF是等边三角形;
(2)记AG、EF交点为H,
∵△AEF是等边三角形,且AE与AF关于AG对称,
∴∠EAG=30°,AG⊥EF,
∵AB与AG关于AE对称,
∴∠BAE=∠GAE=30°,∠AEB=90°,
∵AB=2,
∴BE=1、DF=AF=AE=,
则EH=AE=、AH=,
∴S△ADF=××=.
18.(1)证明:∵CD=CB,点E为BD的中点,
∴CE⊥BD,
∵点F为AC的中点,
∴EF=AC;
(2)解:∵∠BAC=45°,CE⊥BD,
∴△AEC是等腰直角三角形,
∵点F为AC的中点,
∴EF垂直平分AC,
∴AM=CM,
∵CD=CM+DM=AM+DM,CD=CB,
∴BC=AM+DM.
19.解:(1)过A作AD⊥BC,交BC的延长线于点D,如图1所示:
在Rt△ADC中,AC=4,
∵∠C=150°,
∴∠ACD=30°,
∴AD=AC=2,
CD=AC?cos30°=4×=2,
在Rt△ABD中,tanB===,
∴BD=16,
∴BC=BD﹣CD=16﹣2;
(2)在BC边上取一点M,使得CM=AC,连接AM,如图2所示:
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,
tan15°=tan∠AMD====2﹣≈0.27≈0.3.
20.解:如图,设∠α为直角三角形的一个锐角,
∵cosα=,
∴设α的邻边为1k,斜边为3k,
由勾股定理,得α的对边为=2k,
∴tanα=2,sinα=,
故=2+
=2+3﹣2=3.
