实际生活中的反比例函数
图片预览



文档简介
(共13张PPT)
湘教版九年级下
制作:谢彦文
设计:谢彦文
单位:桥头河镇株木中学
某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.
问题1: 你能解释他们这样做的道理吗
问题2:当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变化
主要是为减小压强而安全通过
由P=F/S可知,当压力一定时,随着木板面积的增大,人和木板对地面的压强减小
身临其境
如果人和木板对湿地地面的压力合计600 N,那么
(1)用含S的代数式表示p,p是S的反比例函数吗 为什么
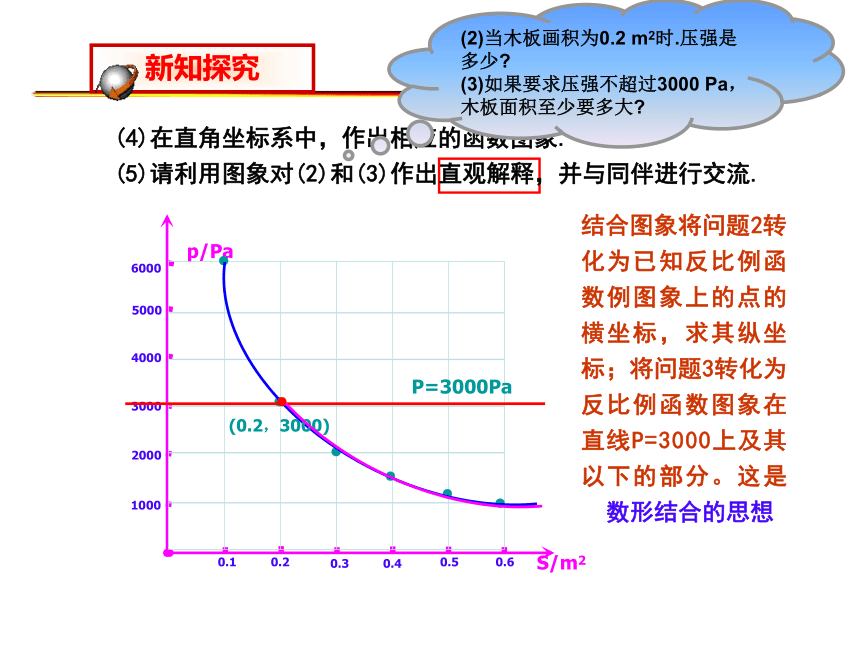
(2)当木板画积为0.2 m2时.压强是多少
(3)如果要求压强不超过3000 Pa,木板面积至少要多大
(3)当p=3000 Pa时,
S= =0.1(m2).
如果要求压强不超过3000 Pa,木板面积至少要0.2 m2.
(2)当S=0.2 m2时, p= =3000(Pa).
(1)由p= 得p= p是S的反比例函数。
新知探究
(4)在直角坐标系中,作出相应的函数图象.
S/m2
p/Pa
0.1
1000
4000
3000
5000
6000
0.2
0.3
0.4
0.5
0.6
2000
●
●
●
●
●
●
P=3000Pa
(0.2,3000)
结合图象将问题2转化为已知反比例函数例图象上的点的横坐标,求其纵坐标;将问题3转化为反比例函数图象在直线P=3000上及其以下的部分。这是
数形结合的思想
新知探究
(2)当木板画积为0.2 m2时.压强是多少
(3)如果要求压强不超过3000 Pa,木板面积至少要多大
(5)请利用图象对(2)和(3)作出直观解释,并与同伴进行交流.
●
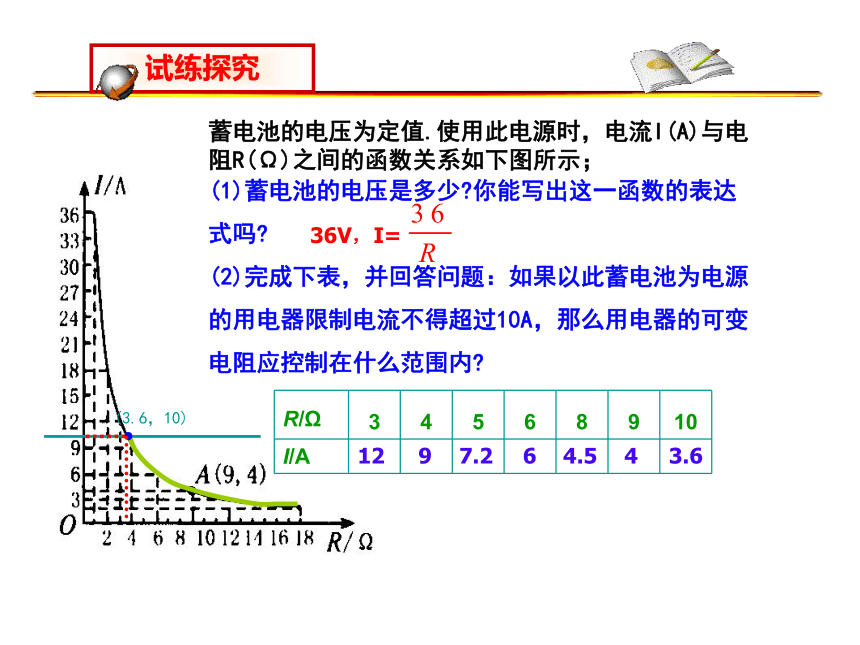
R/Ω 3 4 5 6 8 9 10
I/A
蓄电池的电压为定值.使用此电源时,电流I(A)与电
阻R(Ω)之间的函数关系如下图所示;
36V,I=
12
9
7.2
6
4.5
4
3.6
(3.6,10)
●
试练探究
(1)蓄电池的电压是多少 你能写出这一函数的表达式吗
(2)完成下表,并回答问题:如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内
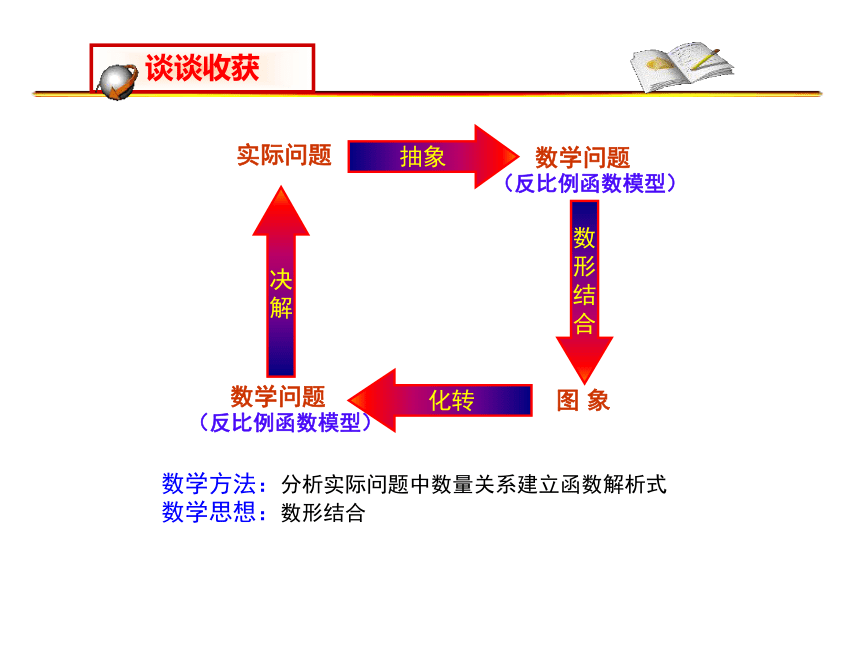
数学方法:分析实际问题中数量关系建立函数解析式
数学思想:数形结合
图 象
实际问题
数学问题
(反比例函数模型)
数学问题
(反比例函数模型)
谈谈收获
抽象
数
形
结
合
化转
决
解
某蓄水池的排水管每时排水8m3,6h可将满池水全部排空.
(1)蓄水池的容积是多少
解:蓄水池的容积为:8×6=48(m3).
(2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化
(3)写出t与Q之间的函数关系式;
解:t与Q之间的函数关系式为:
答:此时所需时间t(h)将减少.
试练反馈
某蓄水池的排水管每时排水8m3,6h可将满池水全部排空.
(4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少
解:当t=5h时,Q=48/5=9.6m3.所以每时的排水量至少为9.6m3.
(5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空
解:当Q=12(m3)时,t=48/12=4(h).所以最少需5h可将满池水全部排空.
(6)画出函数图象,根据图象请对问题(4)和(5)作出直观解释,并和同伴交流.
试练反馈
●
●
●
●
●
●
(5,9.6)
数形结合
4
12
8
16
t/h
Q/m3
4
12
8
16
20
24
20
如图,为了预防“非典”,某学校对教室采用药熏消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例,现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg。请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y与x的关系式为 ;
(2)药物燃烧完后,y与x的关系式为 ;
Y= x(0Y= (x≥8)
中考链接
(3)研究表明,当空气中每立方米的含药量低于1.6 mg时学生方可进入教室,那么从消毒开始,至少经过多少min后,学生才能回到教室;研究表明,当空气中每 立方米的含药量不低于3mg且持续时间不低于10 min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?请说明理由。
●
(30,1.6)
●
●
(4,3)
(16,3)
中考链接
1.某地上年度电价为0.8元,年用电量为1亿度,本年度
计划将电价调至0.55-0.75之间,经测算若电价调至X元,
则本年度新增用电量y(亿·度)与(X-0.4)元成反比例,
又当x=0.65时,y=0.8,求y与x之间的函数关系式。
2.水池内装有12m3的水,如果从排水管中每小时流出xm3的水,则经过y小时,就可以把水放完。
①求y与x的函数关系式。
②画出函数的图象。
③当x=6 m3/小时,求时间y的值
课后练习
湘教版九年级下
制作:谢彦文
设计:谢彦文
单位:桥头河镇株木中学
某科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全迅速通过这片湿地,他们沿着前进路线铺垫了若干木板,构筑了一条临时通道,从而顺利完成了任务.
问题1: 你能解释他们这样做的道理吗
问题2:当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强P(Pa)将如何变化
主要是为减小压强而安全通过
由P=F/S可知,当压力一定时,随着木板面积的增大,人和木板对地面的压强减小
身临其境
如果人和木板对湿地地面的压力合计600 N,那么
(1)用含S的代数式表示p,p是S的反比例函数吗 为什么
(2)当木板画积为0.2 m2时.压强是多少
(3)如果要求压强不超过3000 Pa,木板面积至少要多大
(3)当p=3000 Pa时,
S= =0.1(m2).
如果要求压强不超过3000 Pa,木板面积至少要0.2 m2.
(2)当S=0.2 m2时, p= =3000(Pa).
(1)由p= 得p= p是S的反比例函数。
新知探究
(4)在直角坐标系中,作出相应的函数图象.
S/m2
p/Pa
0.1
1000
4000
3000
5000
6000
0.2
0.3
0.4
0.5
0.6
2000
●
●
●
●
●
●
P=3000Pa
(0.2,3000)
结合图象将问题2转化为已知反比例函数例图象上的点的横坐标,求其纵坐标;将问题3转化为反比例函数图象在直线P=3000上及其以下的部分。这是
数形结合的思想
新知探究
(2)当木板画积为0.2 m2时.压强是多少
(3)如果要求压强不超过3000 Pa,木板面积至少要多大
(5)请利用图象对(2)和(3)作出直观解释,并与同伴进行交流.
●
R/Ω 3 4 5 6 8 9 10
I/A
蓄电池的电压为定值.使用此电源时,电流I(A)与电
阻R(Ω)之间的函数关系如下图所示;
36V,I=
12
9
7.2
6
4.5
4
3.6
(3.6,10)
●
试练探究
(1)蓄电池的电压是多少 你能写出这一函数的表达式吗
(2)完成下表,并回答问题:如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内
数学方法:分析实际问题中数量关系建立函数解析式
数学思想:数形结合
图 象
实际问题
数学问题
(反比例函数模型)
数学问题
(反比例函数模型)
谈谈收获
抽象
数
形
结
合
化转
决
解
某蓄水池的排水管每时排水8m3,6h可将满池水全部排空.
(1)蓄水池的容积是多少
解:蓄水池的容积为:8×6=48(m3).
(2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化
(3)写出t与Q之间的函数关系式;
解:t与Q之间的函数关系式为:
答:此时所需时间t(h)将减少.
试练反馈
某蓄水池的排水管每时排水8m3,6h可将满池水全部排空.
(4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少
解:当t=5h时,Q=48/5=9.6m3.所以每时的排水量至少为9.6m3.
(5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空
解:当Q=12(m3)时,t=48/12=4(h).所以最少需5h可将满池水全部排空.
(6)画出函数图象,根据图象请对问题(4)和(5)作出直观解释,并和同伴交流.
试练反馈
●
●
●
●
●
●
(5,9.6)
数形结合
4
12
8
16
t/h
Q/m3
4
12
8
16
20
24
20
如图,为了预防“非典”,某学校对教室采用药熏消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例,现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg。请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y与x的关系式为 ;
(2)药物燃烧完后,y与x的关系式为 ;
Y= x(0
中考链接
(3)研究表明,当空气中每立方米的含药量低于1.6 mg时学生方可进入教室,那么从消毒开始,至少经过多少min后,学生才能回到教室;研究表明,当空气中每 立方米的含药量不低于3mg且持续时间不低于10 min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?请说明理由。
●
(30,1.6)
●
●
(4,3)
(16,3)
中考链接
1.某地上年度电价为0.8元,年用电量为1亿度,本年度
计划将电价调至0.55-0.75之间,经测算若电价调至X元,
则本年度新增用电量y(亿·度)与(X-0.4)元成反比例,
又当x=0.65时,y=0.8,求y与x之间的函数关系式。
2.水池内装有12m3的水,如果从排水管中每小时流出xm3的水,则经过y小时,就可以把水放完。
①求y与x的函数关系式。
②画出函数的图象。
③当x=6 m3/小时,求时间y的值
课后练习
