人教版 九年级上册数学 24.3正多边形和圆 同步练习(Word版 含解析)
文档属性
| 名称 | 人教版 九年级上册数学 24.3正多边形和圆 同步练习(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 108.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-14 05:29:58 | ||
图片预览

文档简介
24.3正多边形和圆
同步练习
一.选择题
1.若一个圆内接正多边形的中心角是36°,则这个多边形是( )
A.正五边形
B.正八边形
C.正十边形
D.正十八边形
2.正六边形的周长为6,则它的外接圆半径为( )
A.1
B.2
C.3
D.6
3.若一个正六边形的半径为2,则它的边心距等于( )
A.2
B.1
C.
D.2
4.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CDB的度数是( )
A.90°
B.60°
C.45°
D.30°
5.如图,已知边长为2cm的正六边形ABCDEF,点A1,B1,C1,D1,E1,F1分别为所在各边的中点,则图中阴影部分的总面积是( )
A.
B.
C.
D.
6.若一个圆的内接正三角形、正方形、正六边形的边心距分别为r1,r2,r3,则r1:r2:r3等于( )
A.1:2:3
B.::1
C.1::
D.3:2:1
7.有一边长为的正三角形,则它的外接圆的面积为( )
A.
B.
C.4π
D.12π
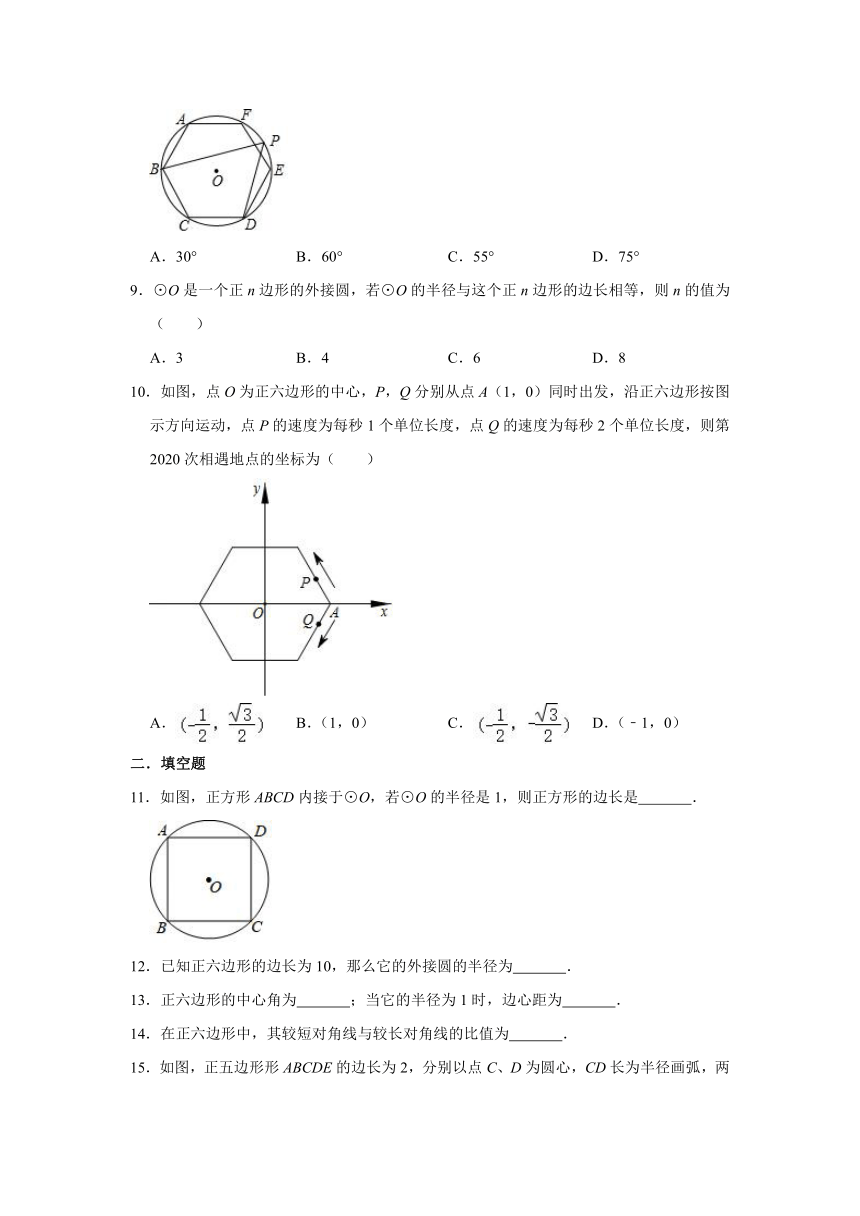
8.如图,⊙O是正六边形ABCDEF的外接圆,P是弧EF上一点,则∠BPD的度数是( )
A.30°
B.60°
C.55°
D.75°
9.⊙O是一个正n边形的外接圆,若⊙O的半径与这个正n边形的边长相等,则n的值为( )
A.3
B.4
C.6
D.8
10.如图,点O为正六边形的中心,P,Q分别从点A(1,0)同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2020次相遇地点的坐标为( )
A.
B.(1,0)
C.
D.(﹣1,0)
二.填空题
11.如图,正方形ABCD内接于⊙O,若⊙O的半径是1,则正方形的边长是
.
12.已知正六边形的边长为10,那么它的外接圆的半径为
.
13.正六边形的中心角为
;当它的半径为1时,边心距为
.
14.在正六边形中,其较短对角线与较长对角线的比值为
.
15.如图,正五边形形ABCDE的边长为2,分别以点C、D为圆心,CD长为半径画弧,两弧交于点F,则的长为
.(结果保留π)
三.解答题
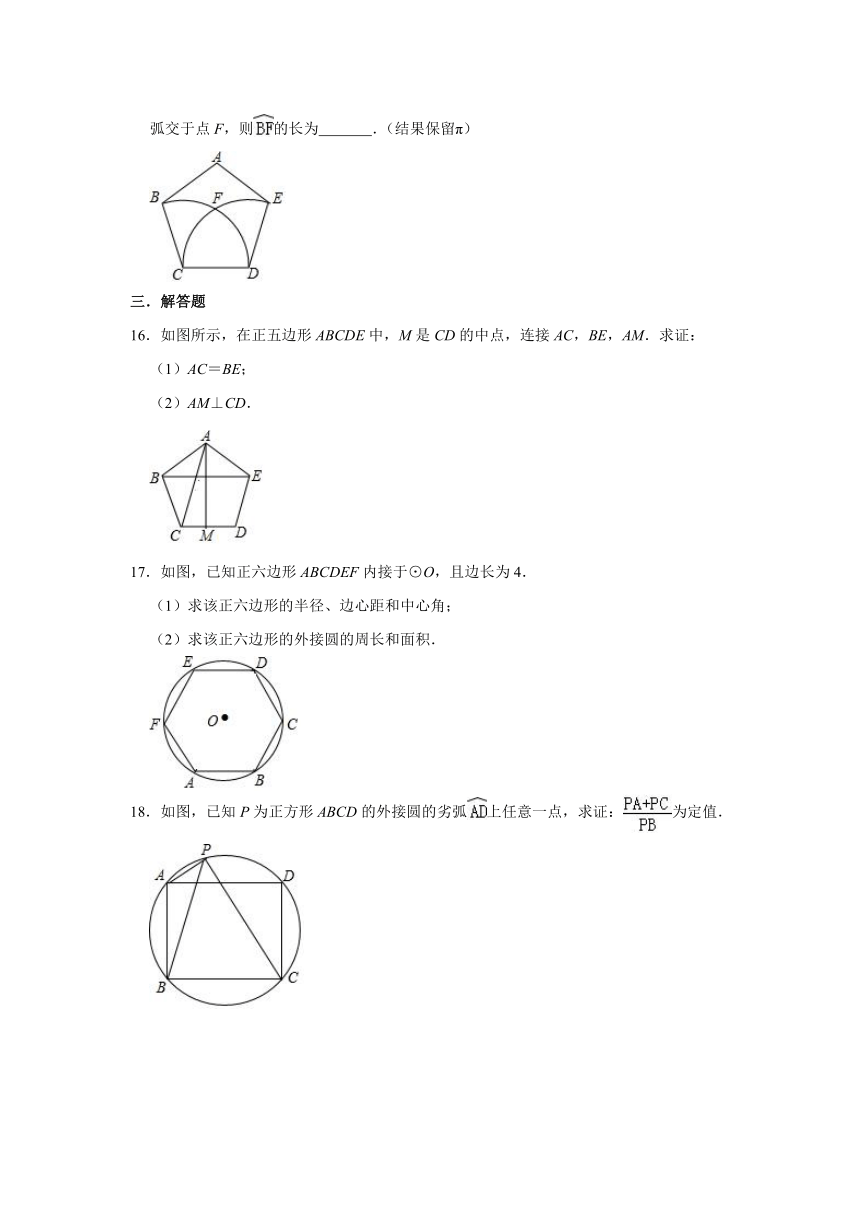
16.如图所示,在正五边形ABCDE中,M是CD的中点,连接AC,BE,AM.求证:
(1)AC=BE;
(2)AM⊥CD.
17.如图,已知正六边形ABCDEF内接于⊙O,且边长为4.
(1)求该正六边形的半径、边心距和中心角;
(2)求该正六边形的外接圆的周长和面积.
18.如图,已知P为正方形ABCD的外接圆的劣弧上任意一点,求证:为定值.
参考答案
1.C
2.A
3.C
4.D
5.A
6.C
7.C
8.B
9.C
10.A
11.
12.10
13.60°,
14.:2
15.π
16.证明:(1)∵五边形ABCDE是正五边形,
∴AB=BC=AE,∠ABC=∠BAE,
在△ABC和△EAB中,
,
∴△ABC≌△EAB,
∴AC=BE;
(2)连接AD,
由(1)的方法可以证明△ABC≌△AED,
∴AC=AD,又M是CD的中点,
∴AM⊥CD.
17.解:如图,AB为⊙0的内接正六边形的一边,连接OA、OB;
过点O作OM⊥AB于点M;
∵六边形ABCDEF为正六边形,
∴OA=OB,∠AOB==60°;
∴△OAB为等边三角形,
∴OA=AB=4;
∵OM⊥AB,
∴∠AOM=∠BOM=30°,AM=AB=2,
∴OM=AM=2;
(2)正六边形的外接圆的周长=2π×OA=8π;
外接圆的面积=π×42=16π.
18.解:延长PA到E,使AE=PC,连接BE,
∵∠BAE+∠BAP=180°,∠BAP+∠PCB=180°,
∴∠BAE=∠PCB,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
在△ABE和△CBP中,
,
∴△ABE≌△CBP(SAS),
∴∠ABE=∠CBP,BE=BP,
∴∠ABE+∠ABP=∠ABP+∠CBP=90°,
∴△BEP是等腰直角三角形,
∴PA+PC=PE=PB.
即:=,
∴为定值.
同步练习
一.选择题
1.若一个圆内接正多边形的中心角是36°,则这个多边形是( )
A.正五边形
B.正八边形
C.正十边形
D.正十八边形
2.正六边形的周长为6,则它的外接圆半径为( )
A.1
B.2
C.3
D.6
3.若一个正六边形的半径为2,则它的边心距等于( )
A.2
B.1
C.
D.2
4.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CDB的度数是( )
A.90°
B.60°
C.45°
D.30°
5.如图,已知边长为2cm的正六边形ABCDEF,点A1,B1,C1,D1,E1,F1分别为所在各边的中点,则图中阴影部分的总面积是( )
A.
B.
C.
D.
6.若一个圆的内接正三角形、正方形、正六边形的边心距分别为r1,r2,r3,则r1:r2:r3等于( )
A.1:2:3
B.::1
C.1::
D.3:2:1
7.有一边长为的正三角形,则它的外接圆的面积为( )
A.
B.
C.4π
D.12π
8.如图,⊙O是正六边形ABCDEF的外接圆,P是弧EF上一点,则∠BPD的度数是( )
A.30°
B.60°
C.55°
D.75°
9.⊙O是一个正n边形的外接圆,若⊙O的半径与这个正n边形的边长相等,则n的值为( )
A.3
B.4
C.6
D.8
10.如图,点O为正六边形的中心,P,Q分别从点A(1,0)同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2020次相遇地点的坐标为( )
A.
B.(1,0)
C.
D.(﹣1,0)
二.填空题
11.如图,正方形ABCD内接于⊙O,若⊙O的半径是1,则正方形的边长是
.
12.已知正六边形的边长为10,那么它的外接圆的半径为
.
13.正六边形的中心角为
;当它的半径为1时,边心距为
.
14.在正六边形中,其较短对角线与较长对角线的比值为
.
15.如图,正五边形形ABCDE的边长为2,分别以点C、D为圆心,CD长为半径画弧,两弧交于点F,则的长为
.(结果保留π)
三.解答题
16.如图所示,在正五边形ABCDE中,M是CD的中点,连接AC,BE,AM.求证:
(1)AC=BE;
(2)AM⊥CD.
17.如图,已知正六边形ABCDEF内接于⊙O,且边长为4.
(1)求该正六边形的半径、边心距和中心角;
(2)求该正六边形的外接圆的周长和面积.
18.如图,已知P为正方形ABCD的外接圆的劣弧上任意一点,求证:为定值.
参考答案
1.C
2.A
3.C
4.D
5.A
6.C
7.C
8.B
9.C
10.A
11.
12.10
13.60°,
14.:2
15.π
16.证明:(1)∵五边形ABCDE是正五边形,
∴AB=BC=AE,∠ABC=∠BAE,
在△ABC和△EAB中,
,
∴△ABC≌△EAB,
∴AC=BE;
(2)连接AD,
由(1)的方法可以证明△ABC≌△AED,
∴AC=AD,又M是CD的中点,
∴AM⊥CD.
17.解:如图,AB为⊙0的内接正六边形的一边,连接OA、OB;
过点O作OM⊥AB于点M;
∵六边形ABCDEF为正六边形,
∴OA=OB,∠AOB==60°;
∴△OAB为等边三角形,
∴OA=AB=4;
∵OM⊥AB,
∴∠AOM=∠BOM=30°,AM=AB=2,
∴OM=AM=2;
(2)正六边形的外接圆的周长=2π×OA=8π;
外接圆的面积=π×42=16π.
18.解:延长PA到E,使AE=PC,连接BE,
∵∠BAE+∠BAP=180°,∠BAP+∠PCB=180°,
∴∠BAE=∠PCB,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
在△ABE和△CBP中,
,
∴△ABE≌△CBP(SAS),
∴∠ABE=∠CBP,BE=BP,
∴∠ABE+∠ABP=∠ABP+∠CBP=90°,
∴△BEP是等腰直角三角形,
∴PA+PC=PE=PB.
即:=,
∴为定值.
同课章节目录
