高中物理人教版选修3.4 作业题 13.2 全反射 Word版含解析
文档属性
| 名称 | 高中物理人教版选修3.4 作业题 13.2 全反射 Word版含解析 |
|
|
| 格式 | DOC | ||
| 文件大小 | 331.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-14 13:27:26 | ||
图片预览



文档简介
全反射
一、选择题(1~6为单选,7~9为多选)
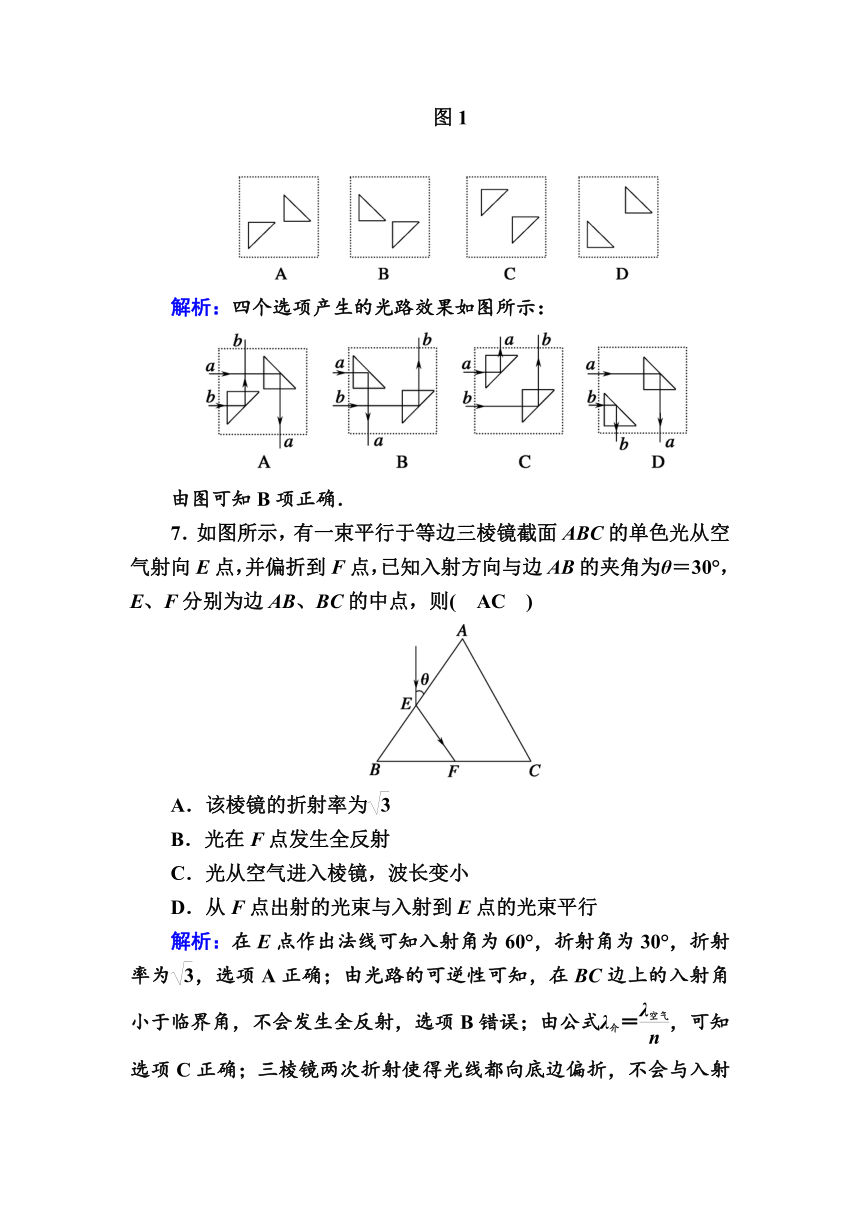
1.如图,一个三棱镜的截面为等腰直角△ABC,∠A为直角,此截面所在平面内的光线沿平行于BC边的方向射到AB边,进入棱镜后直接射到AC边上,并刚好能发生全反射.该棱镜材料的折射率为( A )
A. B.
C. D.
解析:光路图如图所示,设光在AB边上的折射角为γ,在AC边发生全反射的临界角为C,则C=90°-γ,由折射定律得,n=,sinC=,联立以上式子得,n=,A项正确.
2.自行车的尾灯采用了全反射棱镜的原理,它虽然本身不发光,但在夜间骑行时,从后面开来的汽车发出的强光照到尾灯后,会有较强的光被反射回去,使汽车司机注意到前面有自行车.尾灯的构造如图所示.下面说法正确的是( C )
A.汽车灯光应从左面射过来,在尾灯的左表面发生全反射
B.汽车灯光应从左面射过来,在尾灯的右表面发生全反射
C.汽车灯光应从右面射过来,在尾灯的左表面发生全反射
D.汽车灯光应从右面射过来,在尾灯的右表面发生全反射
解析:光从空气进入尾灯,不发生全反射,从尾灯射向空气时发生全反射.
3.高速公路上的标志牌常用“回归反光膜”制成,夜间行车时,它能将车灯照射过来的光逆向返回,标志牌上的字特别醒目.这种“回归反光膜”是用球体反射元件制成的.如图所示,反光膜内均匀分布着直径为10 μm的细玻璃珠,所用玻璃的折射率为,为使入射的车灯光线经玻璃珠的折射、反射、再折射后恰好和入射光线平行,那么第一次入射时的入射角是( A )
A.60° B.45°
C.30° D.15°
解析:设入射角为i,折射角为θ,作出光路图如图所示.因为出射光线恰好和入射光线平行,所以i=2θ,根据折射定律有==,所以θ=30°,i=2θ=60°.选项A正确.
4.夏天的海面上常会出现海市蜃楼奇观,这是由于光在大气中的折射和全反射使远处物体在空中形成的( A )
A.正立虚像 B.倒立虚像
C.正立实像 D.倒立实像
解析:海面的蜃景是正立虚像,沙漠中的蜃景是倒立虚像.
5.下图是一段因拉伸速度不均匀而形成的不合格光纤产品,呈圆台形.一单色光射到上边界O点并射出光纤,进入真空中时,入射角为30°,折射角为53°(sin53°=0.8),则( B )
A.此光纤的折射率为0.625
B.该单色光在光纤中的传播速度为1.875×108 m/s
C.减小单色光在O点的入射角可以提高光能传输效率
D.同一单色光在此光纤内的全反射临界角比在圆柱形光纤中大
解析:此光纤的折射率为n==1.6,选项A错误;该单色光在光纤中的传播速度为v==1.875×108 m/s,选项B正确;要提高光能传输效率,就要减小光的折射,故应增大单色光在O点的入射角,选项C错误;全反射的临界角由折射率和介质决定,入射光和光纤材料不变,只是光纤的形状发生改变时,全反射的临界角保持不变,选项D错误.
6.空气中两条光线a和b从方框左侧入射,分别从方框下方和上方射出,其框外光线如图1所示,方框内有两个折射率n=1.5的全反射玻璃棱镜,下列选项中给出了两棱镜四种放置方式的示意图.其中能产生如图所示效果的是( B )
图1
解析:四个选项产生的光路效果如图所示:
由图可知B项正确.
7.如图所示,有一束平行于等边三棱镜截面ABC的单色光从空气射向E点,并偏折到F点,已知入射方向与边AB的夹角为θ=30°,E、F分别为边AB、BC的中点,则( AC )
A.该棱镜的折射率为
B.光在F点发生全反射
C.光从空气进入棱镜,波长变小
D.从F点出射的光束与入射到E点的光束平行
解析:在E点作出法线可知入射角为60°,折射角为30°,折射率为,选项A正确;由光路的可逆性可知,在BC边上的入射角小于临界角,不会发生全反射,选项B错误;由公式λ介=,可知选项C正确;三棱镜两次折射使得光线都向底边偏折,不会与入射到E点的光束平行,故选项D错误.
8.如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=r.现有一束单色光垂直于水平端面A射入透明柱体,只经过两次全反射就垂直于水平端面B射出,设透明柱体的折射率为n,光在透明柱体内传播时间为t,若真空中的光速为c,则( AB )
A.n可能为 B.n可能为2
C.t可能为 D.t可能为
解析:根据题意可画出光路图如图所示,则两次全反射时的入射角为45°,所以全反射的临界角C≤45°,折射率n≥=,A、B项均正确;波在介质中的传播速度v=≤,所以传播时间t=≥,C、D两项均错误.
9.如图所示,半径为R的半圆形透明材料,折射率n=2.一束平行光从空气以垂直于其底面的方向射入,则下述正确的是( BD )
A.所有光线都能通过这种材料
B.只有距圆心O两侧范围内的光才能通过
C.射出的光束会形成发散光束
D.射出的光束会形成会聚光束
解析:平行光射到底面时,光线与界面垂直,方向不变,继续射到球面时,距圆心O两侧范围内的光线入射角小于临界角C=arcsin=30°,发生折射形成会聚光束,范围外的光线入射角大于等于临界角发生全反射.
二、非选择题
10.某同学用大头针、三角板、量角器等器材测半圆形玻璃砖的折射率.开始玻璃砖的位置如图中实线所示,使大头针P1、P2与圆心O在同一直线上,该直线垂直于玻璃砖的直径边,然后使玻璃砖绕圆心O缓慢转动,同时在玻璃砖的直径边一侧观察P1、P2的像,且使P2的像挡住P1的像.当玻璃砖转到图中虚线位置时,上述现象恰好消失.此时只须测量出玻璃砖直径边绕O点转过的角度θ,即可计算出玻璃砖的折射率.请用你的测量量表示出折射率n=.
解析:若半圆形玻璃砖转过θ角时在半圆形玻璃砖直径边一侧恰好看不到P1、P2的像,那么此时恰好发生了全反射.如图所示,过P1、P2的光线在玻璃砖内的入射角为θ,在空气中折射角为90°,根据折射定律得n==,只要测出θ,就可求出玻璃砖的折射率.
11.一足够深的水池内盛有某种透明液体,液体的深度为H,在水池的底部中央放一点光源,其中一条光线以30°入射角射到液体与空气的界面上,它的反射光线与折射光线的夹角为105°,如图所示.求:
(1)这种液体的折射率;
(2)液体表面亮斑的面积.
答案:(1) (2)πH2
解析:(1)由于反射光线与折射光线的夹角为105°,入射角i=30°,则折射角r=45°,故n==.
(2)sinC==,C=45°.
所以亮斑的半径R=H,光斑面积S=πR2=πH2.
12.如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线).已知玻璃的折射率为1.5.现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线).求:
(1)从球面射出的光线对应的入射光线与光轴距离的最大值;
(2)距光轴的入射光线经球面折射后与光轴的交点到O点的距离.
答案:
(1)R (2)2.74R
解析:(1)如图,从底面上A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角ic时,对应入射光线到光轴的距离最大,设最大距离为l.
i=ic①
设n是玻璃的折射率,由全反射临界角的定义有nsinic=1②
由几何关系有sini=③
联立①②③式并利用题给条件,得l=R④
(2)设与光轴相距的光线在球面B点发生折射时的入射角和折射角分别为i1和r1,由折射定律有nsini1=sinr1⑤
设折射光线与光轴的交点为C,在△OBC中,由正弦定理有
=⑥
由几何关系有∠C=r1-i1⑦
sini1=⑧
联立⑤⑥⑦⑧式及题给条件得OC=R≈2.74R⑨
一、选择题(1~6为单选,7~9为多选)
1.如图,一个三棱镜的截面为等腰直角△ABC,∠A为直角,此截面所在平面内的光线沿平行于BC边的方向射到AB边,进入棱镜后直接射到AC边上,并刚好能发生全反射.该棱镜材料的折射率为( A )
A. B.
C. D.
解析:光路图如图所示,设光在AB边上的折射角为γ,在AC边发生全反射的临界角为C,则C=90°-γ,由折射定律得,n=,sinC=,联立以上式子得,n=,A项正确.
2.自行车的尾灯采用了全反射棱镜的原理,它虽然本身不发光,但在夜间骑行时,从后面开来的汽车发出的强光照到尾灯后,会有较强的光被反射回去,使汽车司机注意到前面有自行车.尾灯的构造如图所示.下面说法正确的是( C )
A.汽车灯光应从左面射过来,在尾灯的左表面发生全反射
B.汽车灯光应从左面射过来,在尾灯的右表面发生全反射
C.汽车灯光应从右面射过来,在尾灯的左表面发生全反射
D.汽车灯光应从右面射过来,在尾灯的右表面发生全反射
解析:光从空气进入尾灯,不发生全反射,从尾灯射向空气时发生全反射.
3.高速公路上的标志牌常用“回归反光膜”制成,夜间行车时,它能将车灯照射过来的光逆向返回,标志牌上的字特别醒目.这种“回归反光膜”是用球体反射元件制成的.如图所示,反光膜内均匀分布着直径为10 μm的细玻璃珠,所用玻璃的折射率为,为使入射的车灯光线经玻璃珠的折射、反射、再折射后恰好和入射光线平行,那么第一次入射时的入射角是( A )
A.60° B.45°
C.30° D.15°
解析:设入射角为i,折射角为θ,作出光路图如图所示.因为出射光线恰好和入射光线平行,所以i=2θ,根据折射定律有==,所以θ=30°,i=2θ=60°.选项A正确.
4.夏天的海面上常会出现海市蜃楼奇观,这是由于光在大气中的折射和全反射使远处物体在空中形成的( A )
A.正立虚像 B.倒立虚像
C.正立实像 D.倒立实像
解析:海面的蜃景是正立虚像,沙漠中的蜃景是倒立虚像.
5.下图是一段因拉伸速度不均匀而形成的不合格光纤产品,呈圆台形.一单色光射到上边界O点并射出光纤,进入真空中时,入射角为30°,折射角为53°(sin53°=0.8),则( B )
A.此光纤的折射率为0.625
B.该单色光在光纤中的传播速度为1.875×108 m/s
C.减小单色光在O点的入射角可以提高光能传输效率
D.同一单色光在此光纤内的全反射临界角比在圆柱形光纤中大
解析:此光纤的折射率为n==1.6,选项A错误;该单色光在光纤中的传播速度为v==1.875×108 m/s,选项B正确;要提高光能传输效率,就要减小光的折射,故应增大单色光在O点的入射角,选项C错误;全反射的临界角由折射率和介质决定,入射光和光纤材料不变,只是光纤的形状发生改变时,全反射的临界角保持不变,选项D错误.
6.空气中两条光线a和b从方框左侧入射,分别从方框下方和上方射出,其框外光线如图1所示,方框内有两个折射率n=1.5的全反射玻璃棱镜,下列选项中给出了两棱镜四种放置方式的示意图.其中能产生如图所示效果的是( B )
图1
解析:四个选项产生的光路效果如图所示:
由图可知B项正确.
7.如图所示,有一束平行于等边三棱镜截面ABC的单色光从空气射向E点,并偏折到F点,已知入射方向与边AB的夹角为θ=30°,E、F分别为边AB、BC的中点,则( AC )
A.该棱镜的折射率为
B.光在F点发生全反射
C.光从空气进入棱镜,波长变小
D.从F点出射的光束与入射到E点的光束平行
解析:在E点作出法线可知入射角为60°,折射角为30°,折射率为,选项A正确;由光路的可逆性可知,在BC边上的入射角小于临界角,不会发生全反射,选项B错误;由公式λ介=,可知选项C正确;三棱镜两次折射使得光线都向底边偏折,不会与入射到E点的光束平行,故选项D错误.
8.如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=r.现有一束单色光垂直于水平端面A射入透明柱体,只经过两次全反射就垂直于水平端面B射出,设透明柱体的折射率为n,光在透明柱体内传播时间为t,若真空中的光速为c,则( AB )
A.n可能为 B.n可能为2
C.t可能为 D.t可能为
解析:根据题意可画出光路图如图所示,则两次全反射时的入射角为45°,所以全反射的临界角C≤45°,折射率n≥=,A、B项均正确;波在介质中的传播速度v=≤,所以传播时间t=≥,C、D两项均错误.
9.如图所示,半径为R的半圆形透明材料,折射率n=2.一束平行光从空气以垂直于其底面的方向射入,则下述正确的是( BD )
A.所有光线都能通过这种材料
B.只有距圆心O两侧范围内的光才能通过
C.射出的光束会形成发散光束
D.射出的光束会形成会聚光束
解析:平行光射到底面时,光线与界面垂直,方向不变,继续射到球面时,距圆心O两侧范围内的光线入射角小于临界角C=arcsin=30°,发生折射形成会聚光束,范围外的光线入射角大于等于临界角发生全反射.
二、非选择题
10.某同学用大头针、三角板、量角器等器材测半圆形玻璃砖的折射率.开始玻璃砖的位置如图中实线所示,使大头针P1、P2与圆心O在同一直线上,该直线垂直于玻璃砖的直径边,然后使玻璃砖绕圆心O缓慢转动,同时在玻璃砖的直径边一侧观察P1、P2的像,且使P2的像挡住P1的像.当玻璃砖转到图中虚线位置时,上述现象恰好消失.此时只须测量出玻璃砖直径边绕O点转过的角度θ,即可计算出玻璃砖的折射率.请用你的测量量表示出折射率n=.
解析:若半圆形玻璃砖转过θ角时在半圆形玻璃砖直径边一侧恰好看不到P1、P2的像,那么此时恰好发生了全反射.如图所示,过P1、P2的光线在玻璃砖内的入射角为θ,在空气中折射角为90°,根据折射定律得n==,只要测出θ,就可求出玻璃砖的折射率.
11.一足够深的水池内盛有某种透明液体,液体的深度为H,在水池的底部中央放一点光源,其中一条光线以30°入射角射到液体与空气的界面上,它的反射光线与折射光线的夹角为105°,如图所示.求:
(1)这种液体的折射率;
(2)液体表面亮斑的面积.
答案:(1) (2)πH2
解析:(1)由于反射光线与折射光线的夹角为105°,入射角i=30°,则折射角r=45°,故n==.
(2)sinC==,C=45°.
所以亮斑的半径R=H,光斑面积S=πR2=πH2.
12.如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线).已知玻璃的折射率为1.5.现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线).求:
(1)从球面射出的光线对应的入射光线与光轴距离的最大值;
(2)距光轴的入射光线经球面折射后与光轴的交点到O点的距离.
答案:
(1)R (2)2.74R
解析:(1)如图,从底面上A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角ic时,对应入射光线到光轴的距离最大,设最大距离为l.
i=ic①
设n是玻璃的折射率,由全反射临界角的定义有nsinic=1②
由几何关系有sini=③
联立①②③式并利用题给条件,得l=R④
(2)设与光轴相距的光线在球面B点发生折射时的入射角和折射角分别为i1和r1,由折射定律有nsini1=sinr1⑤
设折射光线与光轴的交点为C,在△OBC中,由正弦定理有
=⑥
由几何关系有∠C=r1-i1⑦
sini1=⑧
联立⑤⑥⑦⑧式及题给条件得OC=R≈2.74R⑨
