初中数学青岛版七年级上册第四章4.2简单随机抽样练习题-普通用卷(word版,含解析)
文档属性
| 名称 | 初中数学青岛版七年级上册第四章4.2简单随机抽样练习题-普通用卷(word版,含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 75.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-14 20:42:09 | ||
图片预览




文档简介
初中数学青岛版七年级上册第四章4.2简单随机抽样练习题
一、选择题
某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本是
A.
100
B.
被抽取的100名学生家长
C.
被抽取的100名学生家长的意见
D.
全校学生家长的意见
某地教育系统为了解本地区30000名初中生的体重情况,从中随机抽取了500名初中生的体重进行统计.以下说法正确的是
A.
30000名初中生是总体
B.
500名初中生是总体的一个样本
C.
500名初中生是样本容量
D.
每名初中生的体重是个体
为了解我区八年级2000名学生期中数学考试情况,从中抽取了400名学生的数学成绩进行统计,下列说法正确的是
A.
这种调查方式是普查
B.
每名学生的数学成绩是个体
C.
2000名学生是总体
D.
400名学生是总体的一个样本
为了解七年级4000名学生参加数学统测成绩的情况,从中随机抽取200名学生的数学成绩进行分析.下列说法正确的是
A.
样本容量是200名
B.
每名学生是个体
C.
200名学生的数学成绩是总体的一个样本
D.
4000名学生是总体
袋子中装有8个白球和若干个黑球,除颜色外其他都相同,小华从袋中任意摸出一球,记下颜色后又放回袋中,摇均后又摸出一球,再记下颜色,做了100次后,共有25次摸出白球,据此估计袋中黑球有
A.
24个
B.
20个
C.
16个
D.
30个
某区共有1万名学生参加数学考试,现从中抽取600名考的数学成绩进行统计分析,以下说法正确的是
A.
1万名考生是总体
B.
每名考生的数学成绩是个体
C.
600名考生是总体的一个样本
D.
这是一次成绩普查
为了调查2020年全国115万名艺体生报名情况,随机抽取了3万名考生的报名情况进行调查,在这个问题中样本容量是
A.
115
B.
115万
C.
3万
D.
3
如果整个地区的观众中青少年、成年人、老年人的人数比为3:4:3,要抽取容量为1000的样本,则成年人抽取合适.
A.
300
B.
400
C.
500
D.
1000
我国疫情防控形势积极向好,为做好复学复课前的准备工作,我县某学校为了解全校1500名学生复课后的上学方式,随机抽取了300名学生进行调查,其中有150人乘车上学,50人步行,剩下的选择其他上学方式,该调査中的样本容量是
A.
1500
B.
300
C.
150
D.
50
某校为了了解全校1500名学生家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本的容量是
A.
1500
B.
受调查的全校1500名学生家长的意见
C.
被抽取的100名学生家长的意见
D.
100
二、填空题
某校征集校运会会徽,遴选出甲、乙、丙三种图案.为了解何种图案更受欢迎,随机调查了该校100名学生,其中68名同学喜欢甲图案,若该校共有2000人,根据所学的统计知识可以估计该校喜欢甲图案的学生有______人.
质检部门为了检测某品牌电器的质量,从同一批次共10000件产品中随机柚取100件进行检测,检测出次品5件,由此估计这一批产品中的次品件数是______.
由于新型冠状病毒的影响,我市没有如期开学,但是停课不停学,大石桥市所有初中生进行网课学习,为了调查全市3万余名中学生网课的学习情况,从全市中学随机抽取1500名学生进行问卷调查,则样本容量是______.
为了测算一块600亩试验田里新培育的杂交水稻的产量,随机对其中的50亩杂交水稻的产量进行了检测,在这个问题中,数字50是______.
为了解今年本科毕业生的就业情况,一家网站对签约情况进行了网络调查.到5月底,参加网络调查的13500人中,已有7300人与用人单位签约.在这个问题中,样本容量是______.
三、解答题
由中宣部建设的“学习强国”学习平台正式上线,这是推动习近平新时代中国特色社会主义思想,推进马克思主义学习型政党和学习型社会建设的创新举措.某校党组织随机抽取了部分党员教师某天的学习成绩进行了整理,分成5个小组表示成绩,单位:分,且,根据学习积分绘制出部分频数分布表和部分频数分布直方图,其中第2,第5两组测试成绩人数直方图的高度比为3:1,请结合下列图表中相关数据回答下列问题:
学习积分频数分布表
组别
成绩x分
频数
频率
1
5
2
b
3
15
4
10
5
a
填空:______,______;
补全频数分布直方图;
据统计,该校共有党员教师200人,请你估计每天学习成绩在40分以上的党员教师人数.
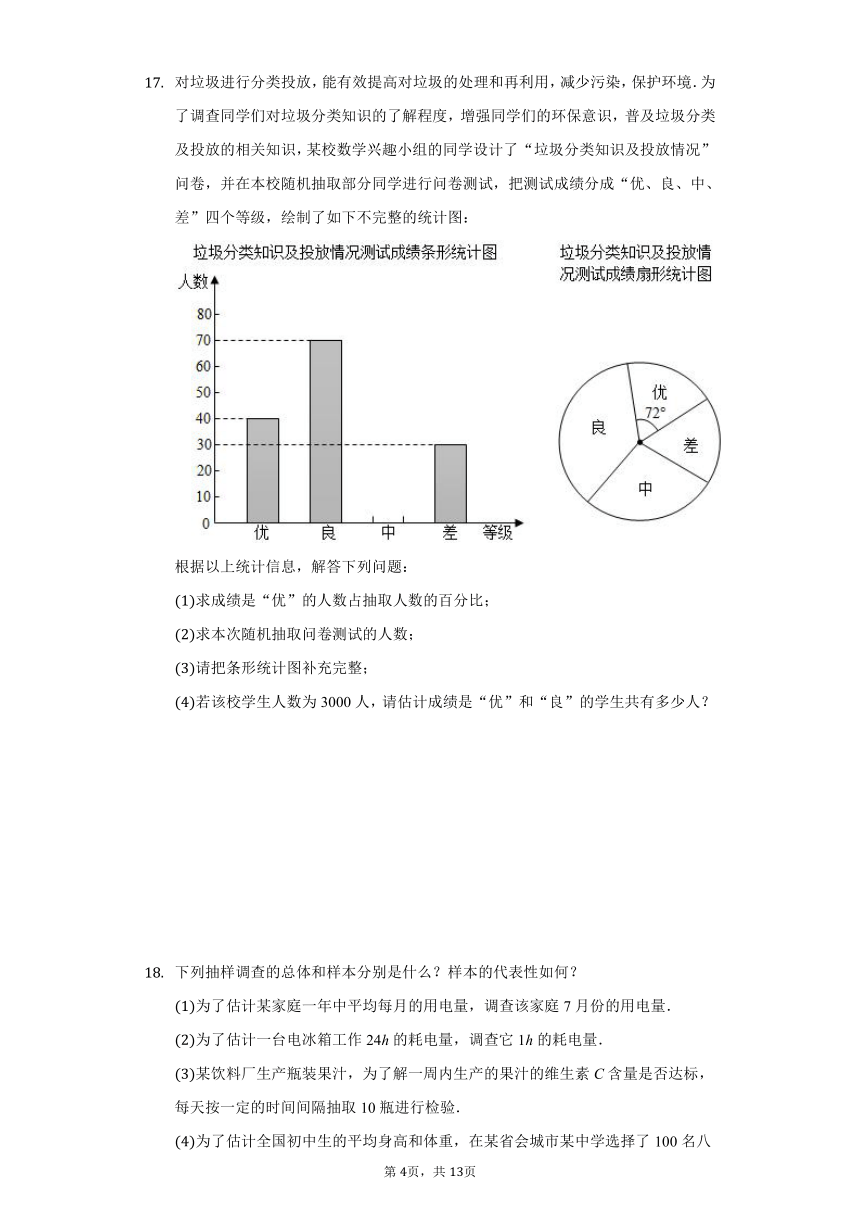
对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了如下不完整的统计图:
根据以上统计信息,解答下列问题:
求成绩是“优”的人数占抽取人数的百分比;
求本次随机抽取问卷测试的人数;
请把条形统计图补充完整;
若该校学生人数为3000人,请估计成绩是“优”和“良”的学生共有多少人?
下列抽样调查的总体和样本分别是什么?样本的代表性如何?
为了估计某家庭一年中平均每月的用电量,调查该家庭7月份的用电量.
为了估计一台电冰箱工作24h的耗电量,调查它1h的耗电量.
某饮料厂生产瓶装果汁,为了解一周内生产的果汁的维生素C含量是否达标,每天按一定的时间间隔抽取10瓶进行检验.
为了估计全国初中生的平均身高和体重,在某省会城市某中学选择了100名八年级的学生进行调查.
答案和解析
1.【答案】C
【解析】解:某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,
这一问题中样本是:被抽取的100名学生家长的意见.
故选:C.
总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
此题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
2.【答案】D
【解析】解:A、30000名初中生是总体,说法错误,应为30000名初中生的体重是总体,故此选项错误;
B、500名初中生是总体的一个样本,说法错误,应为500名初中生的体重是总体的一个样本,故此选项错误;
C、500名初中生是样本容量,说法错误,应为500是样本容量,故此选项错误;
D、每名初中生的体重是个体,说法正确,故此选项正确;
故选:D.
根据总体:我们把所要考察的对象的全体叫做总体;
个体:把组成总体的每一个考察对象叫做个体;
样本:从总体中取出的一部分个体叫做这个总体的一个样本;
样本容量:一个样本包括的个体数量叫做样本容量分别进行分析即可.
此题主要考查了总体、个体、样本、样本容量,关键是要注意考察对象要说明,样本容量只是个数字,没有单位.
3.【答案】B
【解析】解:这种调查方式是抽样调查,此选项错误;
B.每名学生的数学成绩是个体,此选项正确;
C.2000名学生的数学成绩是总体,此选项错误;
D.400名学生的数学成绩是总体的一个样本,此选项错误;
故选:B.
总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象,从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
本题考查了总体、个体、样本、样本容量的概念,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
4.【答案】C
【解析】解:样本容量是200,故本选项不合题意;
B.每名学生的数学成绩是个体,故本选项不合题意;
C.200名学生的数学成绩是总体的一个样本,故本选项符合题意;
D.4000名学生的数学成绩是总体,故本选项不合题意.
故选:C.
根据总体、个体、样本、样本容量的定义即可判断.
本题考查了总体、个体、样本、样本容量的定义,总体是我们把所要考察的对象的全体,个体是把组成总体的每一个考察对象,样本是从总体中取出的一部分个体叫做这个总体的一个样本;样本容量是一个样本包括的个体数量,样本容量没有单位.
5.【答案】A
【解析】解:由题意可得,
袋中有黑球:个.
故选:A.
根据题意可以计算出总的球数,从而可以得到黑球的数目.
本题考查用样本估计总体,解答本题的关键是明确题意,利用概率的知识解答.
6.【答案】B
【解析】解:A、1万名考生的数学成绩是总体,故说法错误;
B、每名考生的数学成绩是个体,故说法正确;
C、600名考生的数学成绩是总体的一个样本,故说法错误;
D、为了了解这1万名考生的数学成绩,从中抽取了600名考生的数学成绩进行统计分析,这种调查采用了抽样调查的方式,故说法错误,
故选:B.
总体是指考察的对象的全体,个体是总体中的每一个考察的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考察的对象.从而找出总体、个体.
本题考查的是确定总体、个体和样本.解此类题需要注意“考察对象实际应是表示事物某一特征的数据,而非考查的事物.”
7.【答案】C
【解析】解:为了调查2020年全国115万名艺体生报名情况,随机抽取了3万名考生的报名情况进行调查,在这个问题中样本容量是3万.
故选:C.
根据样本容量:一个样本包括的个体数量叫做样本容量可得答案.
此题主要考查了样本容量,关键是掌握样本容量只是个数字,没有单位.
8.【答案】B
【解析】解:因为样本容量为1000,某地区青少年、成年人、老年人的人数比约为3:4:3,
所以成年人的人数所占总人数的,
故成年人应抽取人,
故选:B.
根据青少年、成年人、老年人的人数比约为3:4:3,所以成年人的人数所占总人数的,则根据这个条件就可以求出成年人的人数.
此题主要考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
9.【答案】B
【解析】解:为了解某校1500名学生的上学方式,随机抽取了300名学生进行调查,该调查中的样本容量是:300.
故选:B.
样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.
此题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,样本容量是样本中包含的个体的数目,不能带单位.
10.【答案】D
【解析】解:某校为了了解全校1500名学生家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本的容量是100.
故选:D.
样本容量是指样本中个体的数目,据此即可求解.
本题考查了样本容量的定义,样本容量是样本中包含的个体的数目,不能带单位.
11.【答案】1360
【解析】解:估计该校喜欢甲图案的学生有人,
故答案为:1360.
用总人数乘以样本中喜欢甲图案的人数所占比例即可得.
本题主要考查用样本估计总体,从一个总体得到一个包含大量数据的样本,我们很难从一个个数字中直接看出样本所包含的信息.这时,我们用频率分布直方图来表示相应样本的频率分布,从而去估计总体的分布情况.
12.【答案】500
【解析】解:随机抽取100件进行检测,检测出次品5件,
次品所占的百分比是:,
这一批次产品中的次品件数是:件,
故答案为:500
先求出次品所占的百分比,再根据生产这种零件10000件,直接相乘得出答案即可.
此题主要考查了用样本估计总体,根据出现次品的数量求出次品所占的百分比是解题关键.
13.【答案】1500
【解析】解:样本容量是1500,
故答案为:1500.
总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
14.【答案】样本容量
【解析】解:为了测算一块600亩试验田里新培育的杂交水稻的产量,随机对其中的50亩杂交水稻的产量进行了检测,在这个问题中,数字50是样本容量.
故答案为:样本容量.
根据总体:我们把所要考察的对象的全体叫做总体;样本:从总体中取出的一部分个体叫做这个总体的一个样本;样本容量:一个样本包括的个体数量叫做样本容量可得答案.
此题主要考查了总体、个体、样本、样本容量,关键是掌握定义.注意:样本容量不带单位.
15.【答案】13500
【解析】解:为了解今年本科毕业生的就业情况,一家网站对签约情况进行了网络调查.到5月底,参加网络调查的13500人中,已有7300人与用人单位签约.在这个问题中,样本容量是13500.
故答案为:13500.
根据样本容量:一个样本包括的个体数量叫做样本容量可得答案.
此题主要考查了样本容量,关键是注意样本容量只是个数字,没有单位.
16.【答案】5
?
【解析】解:本次抽取的人数为:,
第2,第5两组测试成绩人数直方图的高度比为3:1,
,,
故答案为:5,;
由知,,则第二组的频数为15,
补全的频数分布直方图如右图所示;
人,
答:每天学习成绩在40分以上的党员教师有120人.
根据第三组的频数和所占的百分比可以求得本次调查的人数,从而可以求得a和b的值;
根据中的结果可以得到第二组和第五组的频数,从而可以将频数分布直方图补充完整;
根据直方图中的数据可以计算出每天学习成绩在40分以上的党员教师人数.
本题考查频数分布直方图、频数分布表、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
17.【答案】解:成绩是“优”的人数占抽取人数的百分比是;
本次随机抽取问卷测试的人数是人;
成绩是“中”的人数是人.
条形统计图补充如下:
人.
答:成绩是“优”和“良”的学生共有6050人.
【解析】用成绩是“优”所在扇形圆心角的度数除以即可;
用成绩是“优”的人数除以所占的百分比即可;
利用总人数减去其它组的人数即可求得成绩是“中”的人数,从而补全条形图;
利用总人数3000乘以成绩是“优”和“良”的学生所占的百分比即可.
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了利用样本估计总体.
18.【答案】解:总体:该家庭一年中平均每月的用电量;
样本:该家庭7月份的用电量.
该样本不具有代表性,
因为7月份气温较高,家庭用电量除了其他月份必须的普通照明,电视之类的,
额外增加了空调等防暑降温的用电器,这样7月份用电量随之增加.
所以根据它了解该家庭一年中平均每月的用电量不准确;
总体:一台电冰箱工作24h的耗电量;
样本:该电冰箱工作1h的耗电量.
该样本具有代表性;
总体:一周内生产的果汁的维生素C含量是否达标;
样本:10瓶果汁的维生素C含量.
该样本具有代表性;
总体:全国初中生的平均身高和体重;
样本:100名八年级的学生的身高和体重.
该样本不具有代表性,因为初中生包括七、八、九年级的学生,
各个年级的学生年龄不同,身高和体重也有所差异,
另外某一城市的学生身高体重不能代表全国,
地域不同,身高体重有所差异.
【解析】根据题意分别进行说明抽样调查的总体和样本、样本的代表性即可.
本题考查了调查收集数据的过程与方法、抽样调查的可靠性,解决本题的关键是掌握总体、样本,解题要分清具体问题中的总体与样本,要明确考查的对象.总体与样本的考查对象是相同的,所不同的是范围的大小.
第2页,共13页
第1页,共13页
一、选择题
某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本是
A.
100
B.
被抽取的100名学生家长
C.
被抽取的100名学生家长的意见
D.
全校学生家长的意见
某地教育系统为了解本地区30000名初中生的体重情况,从中随机抽取了500名初中生的体重进行统计.以下说法正确的是
A.
30000名初中生是总体
B.
500名初中生是总体的一个样本
C.
500名初中生是样本容量
D.
每名初中生的体重是个体
为了解我区八年级2000名学生期中数学考试情况,从中抽取了400名学生的数学成绩进行统计,下列说法正确的是
A.
这种调查方式是普查
B.
每名学生的数学成绩是个体
C.
2000名学生是总体
D.
400名学生是总体的一个样本
为了解七年级4000名学生参加数学统测成绩的情况,从中随机抽取200名学生的数学成绩进行分析.下列说法正确的是
A.
样本容量是200名
B.
每名学生是个体
C.
200名学生的数学成绩是总体的一个样本
D.
4000名学生是总体
袋子中装有8个白球和若干个黑球,除颜色外其他都相同,小华从袋中任意摸出一球,记下颜色后又放回袋中,摇均后又摸出一球,再记下颜色,做了100次后,共有25次摸出白球,据此估计袋中黑球有
A.
24个
B.
20个
C.
16个
D.
30个
某区共有1万名学生参加数学考试,现从中抽取600名考的数学成绩进行统计分析,以下说法正确的是
A.
1万名考生是总体
B.
每名考生的数学成绩是个体
C.
600名考生是总体的一个样本
D.
这是一次成绩普查
为了调查2020年全国115万名艺体生报名情况,随机抽取了3万名考生的报名情况进行调查,在这个问题中样本容量是
A.
115
B.
115万
C.
3万
D.
3
如果整个地区的观众中青少年、成年人、老年人的人数比为3:4:3,要抽取容量为1000的样本,则成年人抽取合适.
A.
300
B.
400
C.
500
D.
1000
我国疫情防控形势积极向好,为做好复学复课前的准备工作,我县某学校为了解全校1500名学生复课后的上学方式,随机抽取了300名学生进行调查,其中有150人乘车上学,50人步行,剩下的选择其他上学方式,该调査中的样本容量是
A.
1500
B.
300
C.
150
D.
50
某校为了了解全校1500名学生家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本的容量是
A.
1500
B.
受调查的全校1500名学生家长的意见
C.
被抽取的100名学生家长的意见
D.
100
二、填空题
某校征集校运会会徽,遴选出甲、乙、丙三种图案.为了解何种图案更受欢迎,随机调查了该校100名学生,其中68名同学喜欢甲图案,若该校共有2000人,根据所学的统计知识可以估计该校喜欢甲图案的学生有______人.
质检部门为了检测某品牌电器的质量,从同一批次共10000件产品中随机柚取100件进行检测,检测出次品5件,由此估计这一批产品中的次品件数是______.
由于新型冠状病毒的影响,我市没有如期开学,但是停课不停学,大石桥市所有初中生进行网课学习,为了调查全市3万余名中学生网课的学习情况,从全市中学随机抽取1500名学生进行问卷调查,则样本容量是______.
为了测算一块600亩试验田里新培育的杂交水稻的产量,随机对其中的50亩杂交水稻的产量进行了检测,在这个问题中,数字50是______.
为了解今年本科毕业生的就业情况,一家网站对签约情况进行了网络调查.到5月底,参加网络调查的13500人中,已有7300人与用人单位签约.在这个问题中,样本容量是______.
三、解答题
由中宣部建设的“学习强国”学习平台正式上线,这是推动习近平新时代中国特色社会主义思想,推进马克思主义学习型政党和学习型社会建设的创新举措.某校党组织随机抽取了部分党员教师某天的学习成绩进行了整理,分成5个小组表示成绩,单位:分,且,根据学习积分绘制出部分频数分布表和部分频数分布直方图,其中第2,第5两组测试成绩人数直方图的高度比为3:1,请结合下列图表中相关数据回答下列问题:
学习积分频数分布表
组别
成绩x分
频数
频率
1
5
2
b
3
15
4
10
5
a
填空:______,______;
补全频数分布直方图;
据统计,该校共有党员教师200人,请你估计每天学习成绩在40分以上的党员教师人数.
对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了如下不完整的统计图:
根据以上统计信息,解答下列问题:
求成绩是“优”的人数占抽取人数的百分比;
求本次随机抽取问卷测试的人数;
请把条形统计图补充完整;
若该校学生人数为3000人,请估计成绩是“优”和“良”的学生共有多少人?
下列抽样调查的总体和样本分别是什么?样本的代表性如何?
为了估计某家庭一年中平均每月的用电量,调查该家庭7月份的用电量.
为了估计一台电冰箱工作24h的耗电量,调查它1h的耗电量.
某饮料厂生产瓶装果汁,为了解一周内生产的果汁的维生素C含量是否达标,每天按一定的时间间隔抽取10瓶进行检验.
为了估计全国初中生的平均身高和体重,在某省会城市某中学选择了100名八年级的学生进行调查.
答案和解析
1.【答案】C
【解析】解:某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,
这一问题中样本是:被抽取的100名学生家长的意见.
故选:C.
总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
此题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
2.【答案】D
【解析】解:A、30000名初中生是总体,说法错误,应为30000名初中生的体重是总体,故此选项错误;
B、500名初中生是总体的一个样本,说法错误,应为500名初中生的体重是总体的一个样本,故此选项错误;
C、500名初中生是样本容量,说法错误,应为500是样本容量,故此选项错误;
D、每名初中生的体重是个体,说法正确,故此选项正确;
故选:D.
根据总体:我们把所要考察的对象的全体叫做总体;
个体:把组成总体的每一个考察对象叫做个体;
样本:从总体中取出的一部分个体叫做这个总体的一个样本;
样本容量:一个样本包括的个体数量叫做样本容量分别进行分析即可.
此题主要考查了总体、个体、样本、样本容量,关键是要注意考察对象要说明,样本容量只是个数字,没有单位.
3.【答案】B
【解析】解:这种调查方式是抽样调查,此选项错误;
B.每名学生的数学成绩是个体,此选项正确;
C.2000名学生的数学成绩是总体,此选项错误;
D.400名学生的数学成绩是总体的一个样本,此选项错误;
故选:B.
总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象,从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
本题考查了总体、个体、样本、样本容量的概念,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
4.【答案】C
【解析】解:样本容量是200,故本选项不合题意;
B.每名学生的数学成绩是个体,故本选项不合题意;
C.200名学生的数学成绩是总体的一个样本,故本选项符合题意;
D.4000名学生的数学成绩是总体,故本选项不合题意.
故选:C.
根据总体、个体、样本、样本容量的定义即可判断.
本题考查了总体、个体、样本、样本容量的定义,总体是我们把所要考察的对象的全体,个体是把组成总体的每一个考察对象,样本是从总体中取出的一部分个体叫做这个总体的一个样本;样本容量是一个样本包括的个体数量,样本容量没有单位.
5.【答案】A
【解析】解:由题意可得,
袋中有黑球:个.
故选:A.
根据题意可以计算出总的球数,从而可以得到黑球的数目.
本题考查用样本估计总体,解答本题的关键是明确题意,利用概率的知识解答.
6.【答案】B
【解析】解:A、1万名考生的数学成绩是总体,故说法错误;
B、每名考生的数学成绩是个体,故说法正确;
C、600名考生的数学成绩是总体的一个样本,故说法错误;
D、为了了解这1万名考生的数学成绩,从中抽取了600名考生的数学成绩进行统计分析,这种调查采用了抽样调查的方式,故说法错误,
故选:B.
总体是指考察的对象的全体,个体是总体中的每一个考察的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考察的对象.从而找出总体、个体.
本题考查的是确定总体、个体和样本.解此类题需要注意“考察对象实际应是表示事物某一特征的数据,而非考查的事物.”
7.【答案】C
【解析】解:为了调查2020年全国115万名艺体生报名情况,随机抽取了3万名考生的报名情况进行调查,在这个问题中样本容量是3万.
故选:C.
根据样本容量:一个样本包括的个体数量叫做样本容量可得答案.
此题主要考查了样本容量,关键是掌握样本容量只是个数字,没有单位.
8.【答案】B
【解析】解:因为样本容量为1000,某地区青少年、成年人、老年人的人数比约为3:4:3,
所以成年人的人数所占总人数的,
故成年人应抽取人,
故选:B.
根据青少年、成年人、老年人的人数比约为3:4:3,所以成年人的人数所占总人数的,则根据这个条件就可以求出成年人的人数.
此题主要考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
9.【答案】B
【解析】解:为了解某校1500名学生的上学方式,随机抽取了300名学生进行调查,该调查中的样本容量是:300.
故选:B.
样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.
此题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,样本容量是样本中包含的个体的数目,不能带单位.
10.【答案】D
【解析】解:某校为了了解全校1500名学生家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本的容量是100.
故选:D.
样本容量是指样本中个体的数目,据此即可求解.
本题考查了样本容量的定义,样本容量是样本中包含的个体的数目,不能带单位.
11.【答案】1360
【解析】解:估计该校喜欢甲图案的学生有人,
故答案为:1360.
用总人数乘以样本中喜欢甲图案的人数所占比例即可得.
本题主要考查用样本估计总体,从一个总体得到一个包含大量数据的样本,我们很难从一个个数字中直接看出样本所包含的信息.这时,我们用频率分布直方图来表示相应样本的频率分布,从而去估计总体的分布情况.
12.【答案】500
【解析】解:随机抽取100件进行检测,检测出次品5件,
次品所占的百分比是:,
这一批次产品中的次品件数是:件,
故答案为:500
先求出次品所占的百分比,再根据生产这种零件10000件,直接相乘得出答案即可.
此题主要考查了用样本估计总体,根据出现次品的数量求出次品所占的百分比是解题关键.
13.【答案】1500
【解析】解:样本容量是1500,
故答案为:1500.
总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
14.【答案】样本容量
【解析】解:为了测算一块600亩试验田里新培育的杂交水稻的产量,随机对其中的50亩杂交水稻的产量进行了检测,在这个问题中,数字50是样本容量.
故答案为:样本容量.
根据总体:我们把所要考察的对象的全体叫做总体;样本:从总体中取出的一部分个体叫做这个总体的一个样本;样本容量:一个样本包括的个体数量叫做样本容量可得答案.
此题主要考查了总体、个体、样本、样本容量,关键是掌握定义.注意:样本容量不带单位.
15.【答案】13500
【解析】解:为了解今年本科毕业生的就业情况,一家网站对签约情况进行了网络调查.到5月底,参加网络调查的13500人中,已有7300人与用人单位签约.在这个问题中,样本容量是13500.
故答案为:13500.
根据样本容量:一个样本包括的个体数量叫做样本容量可得答案.
此题主要考查了样本容量,关键是注意样本容量只是个数字,没有单位.
16.【答案】5
?
【解析】解:本次抽取的人数为:,
第2,第5两组测试成绩人数直方图的高度比为3:1,
,,
故答案为:5,;
由知,,则第二组的频数为15,
补全的频数分布直方图如右图所示;
人,
答:每天学习成绩在40分以上的党员教师有120人.
根据第三组的频数和所占的百分比可以求得本次调查的人数,从而可以求得a和b的值;
根据中的结果可以得到第二组和第五组的频数,从而可以将频数分布直方图补充完整;
根据直方图中的数据可以计算出每天学习成绩在40分以上的党员教师人数.
本题考查频数分布直方图、频数分布表、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
17.【答案】解:成绩是“优”的人数占抽取人数的百分比是;
本次随机抽取问卷测试的人数是人;
成绩是“中”的人数是人.
条形统计图补充如下:
人.
答:成绩是“优”和“良”的学生共有6050人.
【解析】用成绩是“优”所在扇形圆心角的度数除以即可;
用成绩是“优”的人数除以所占的百分比即可;
利用总人数减去其它组的人数即可求得成绩是“中”的人数,从而补全条形图;
利用总人数3000乘以成绩是“优”和“良”的学生所占的百分比即可.
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了利用样本估计总体.
18.【答案】解:总体:该家庭一年中平均每月的用电量;
样本:该家庭7月份的用电量.
该样本不具有代表性,
因为7月份气温较高,家庭用电量除了其他月份必须的普通照明,电视之类的,
额外增加了空调等防暑降温的用电器,这样7月份用电量随之增加.
所以根据它了解该家庭一年中平均每月的用电量不准确;
总体:一台电冰箱工作24h的耗电量;
样本:该电冰箱工作1h的耗电量.
该样本具有代表性;
总体:一周内生产的果汁的维生素C含量是否达标;
样本:10瓶果汁的维生素C含量.
该样本具有代表性;
总体:全国初中生的平均身高和体重;
样本:100名八年级的学生的身高和体重.
该样本不具有代表性,因为初中生包括七、八、九年级的学生,
各个年级的学生年龄不同,身高和体重也有所差异,
另外某一城市的学生身高体重不能代表全国,
地域不同,身高体重有所差异.
【解析】根据题意分别进行说明抽样调查的总体和样本、样本的代表性即可.
本题考查了调查收集数据的过程与方法、抽样调查的可靠性,解决本题的关键是掌握总体、样本,解题要分清具体问题中的总体与样本,要明确考查的对象.总体与样本的考查对象是相同的,所不同的是范围的大小.
第2页,共13页
第1页,共13页
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
