2.1用字母表示数
图片预览

文档简介
2.1《用字母表示数》教案
合肥市行知学校 周向荣
【教学目标】
1、能用字母表示学过的运算律和公式等,感知用字母表示数的优越性;
2、尝试用含字母的式子描述一些问题中的数量关系,培养学生探索问题和归纳问题的能力;
3、体会字母表示数的意义,形成初步的符号感;同时通过数学与生活实际的结合,体会数学给人类带来的美感.
【教学重点】用字母表示数的优越性;体会字母表示数的意义,形成初步的符号感.
【教学难点】用含字母的式子描述一些问题中的数量关系;符号感的形成.
【教学过程】
一.情境导入
练习12×(-),回顾乘法分配率。展现文字语言、符号语言、数字语言,感受其用字母表示数的优越性。顺势回顾其它运算律。
【注意:在说明a、b、c各代表什么时,追问能否都用a来表示、a、b能否表示同一个数;说明数学语言比文字语言更简洁;】
二.举几个用字母表示数的例子。【安排小组交流,代表汇报】
预设:除了运算律外,学生可能不能举出更多的例子,这时老师可以从图形的周长面积、用字母表示数量关系等角度引导;
三.哈利波特的魔法箱
1.k——2k;
2.解决问题2.
预设:可能学生会把k进行分类,讨论如何用含k的式子表示任意一个奇数,这时要肯定孩子的想法,并引导学生会用一个式子表示(抓住定义就行了)
四.日历问题
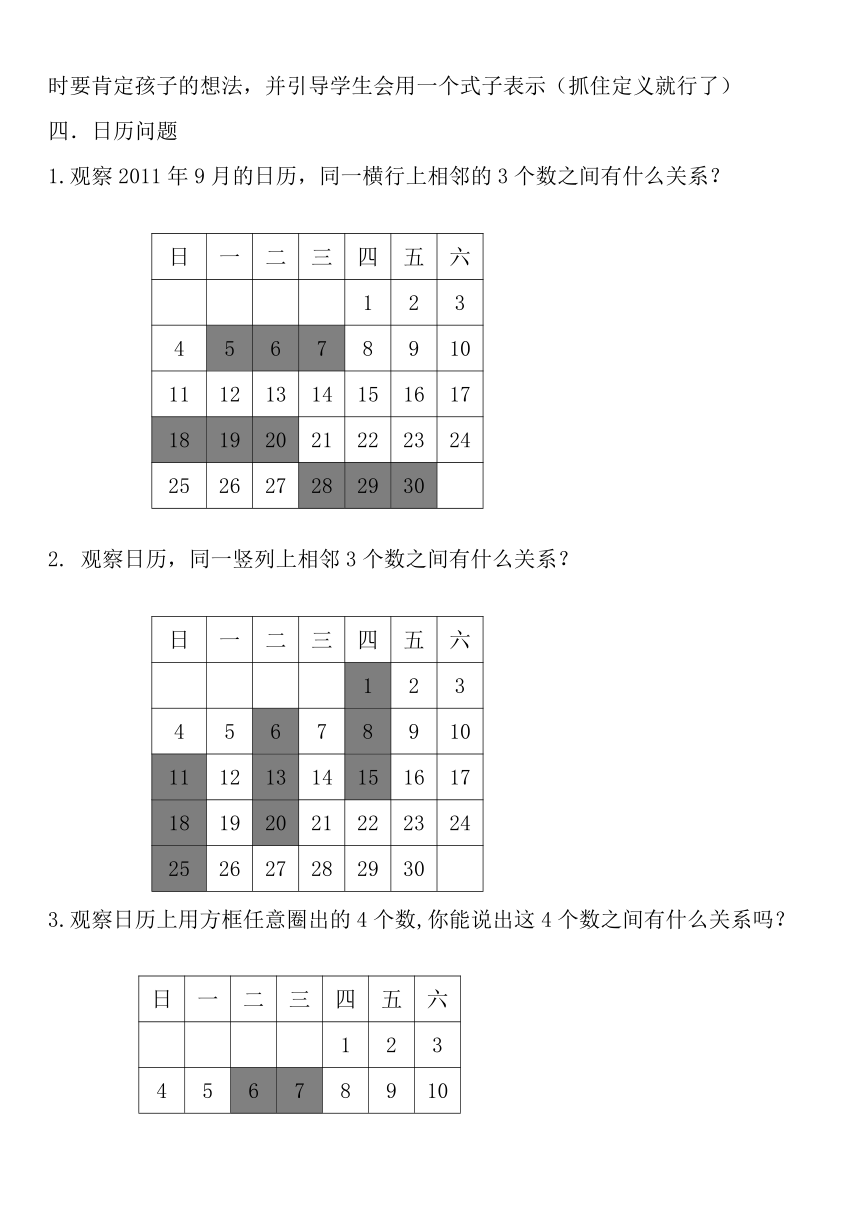
1.观察2011年9月的日历,同一横行上相邻的3个数之间有什么关系?
日 一 二 三 四 五 六
1 2 3
4 5 6 7 8 9 10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30
2. 观察日历,同一竖列上相邻3个数之间有什么关系?
日 一 二 三 四 五 六
1 2 3
4 5 6 7 8 9 10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30
3.观察日历上用方框任意圈出的4个数,你能说出这4个数之间有什么关系吗?
日 一 二 三 四 五 六
1 2 3
4 5 6 7 8 9 10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30
五.随堂练习
用字母表示数——随堂练习
姓名: 评价:共10个空正确的有_____个空
1.一位同学的第二次的测验评价比第一次的进步了10分,若他第二次的评价为a分,那么他第一次的评价为 ______分.
2.某学校的学生共有x人,其中男生占52%,则男生人数为_______,女生人数为______.
3.若a表示三角形的底边的长,h表示三角形的高,S表示这个三角形的面积,则这个三角形的面积公式为 ____ ___.
4.“减去一个数等于加上这个数的相反数”这句话用字母可以表示为:
____ ___.
5.用字母表示三个连续整数: 、 、 .
6.下面为某年某月的月历。观察下列表格,并回答问题:
日 一 二 三 四 五 六
a
b x c
d
请你把a,b,c,d分别用x表示出来:a=_ ___,b=__ __,c=__ __,d=___ __.
参考答案:
1.(a-10);2. 52%x,(1-52%)x或者48%x;3. ;4.a-b=a+(﹣b);
5.a-1、a、a+1;或者a、a+1、a+2;或者a-2、a-1、a;
6. x-7、x-1、x+1;x+7。
六.课堂小结.
1.课堂知识小结
2.布置作业:课本第59页习题2.1,阅读材料。
3.课外阅读材料
课外阅读材料——用字母表示数五注意
1.注意字母具有一般性
用字母可以表示我们已经学过的任意一个有理数,同时随着我们所学知识的深入与需要,数的范围将进一步扩大,字母可以表示今后我们所学到的任何一个数,初学用字母表示数时,同学们一定要深刻理解用字母表示数的这种一般性.比如,字母可以表示正数、负数、零,同学们不要见到就认为是正数,见到–就认为是负数,见到2就认为一定比大,这是对字母表示数的一种极为错误的认识,实际上,不一定就是正数,–不一定就是负数, 2不一定就比大,这要看字母具体代表什么数,当=-2时,-=2,2=-4,即是一个负数,–就是正数, 2反而比要小.
2.注意字母的确定性
它表现在两个方面:一方面是指在同一个问题中,同一个字母只能表示同一个量,不同数量要用不同的字母来表示.比如在同分母分数的加法法则中,虽然、、均表示任意数,但在此等式中,等式两边的、、必须是分别表示同一个数量,即表示相同的分母, 、分别表示两个同分母分数的分子,同样的道理,我们也不能把相同的分母和两个分子用同一个字母来表示;另一方面,在用字母表示数时,一旦式子中的字母的取值确定了,式子的值也就随之确定了,如在圆的周长公式中,如果,那么这个圆的周长就是了.
3.注意字母的不确定性
同一个式子可以表示多种实际问题中的数量关系,如:式子可以表示:“每斤苹果元,买3斤苹果共需3元”,也可以表示:“每枝铅笔元,买3枝铅笔共需3元”等.
4.注意字母的限制性
用字母表示实际问题中的某一个数量时,字母的取值必须使这个问题有意义且符合实际,如“若某型号计算机的单价为元/台,则买台共需元”,这里只能表示正数,只能表示0和正整数.
5.注意字母的抽象性
要逐步理解和接受有些问题的结果可能就是一个用字母表示的式子,如,我们已经习惯于计算“若每小时行30千米,则2小时就会行30×2=60千米”这样的具体结果,因为我们可以想象的到60千米大概有多远.如果换成“若每小时行30千米,则小时就会行30千米”,这样的抽象结果,初学时,有的同学很难接受,因为我们想象不到30千米大概有多远.其实,学习了用字母表示数以后,像30或等这些用字母表示的数,完全可以作为一个结果.
合肥市行知学校 周向荣
【教学目标】
1、能用字母表示学过的运算律和公式等,感知用字母表示数的优越性;
2、尝试用含字母的式子描述一些问题中的数量关系,培养学生探索问题和归纳问题的能力;
3、体会字母表示数的意义,形成初步的符号感;同时通过数学与生活实际的结合,体会数学给人类带来的美感.
【教学重点】用字母表示数的优越性;体会字母表示数的意义,形成初步的符号感.
【教学难点】用含字母的式子描述一些问题中的数量关系;符号感的形成.
【教学过程】
一.情境导入
练习12×(-),回顾乘法分配率。展现文字语言、符号语言、数字语言,感受其用字母表示数的优越性。顺势回顾其它运算律。
【注意:在说明a、b、c各代表什么时,追问能否都用a来表示、a、b能否表示同一个数;说明数学语言比文字语言更简洁;】
二.举几个用字母表示数的例子。【安排小组交流,代表汇报】
预设:除了运算律外,学生可能不能举出更多的例子,这时老师可以从图形的周长面积、用字母表示数量关系等角度引导;
三.哈利波特的魔法箱
1.k——2k;
2.解决问题2.
预设:可能学生会把k进行分类,讨论如何用含k的式子表示任意一个奇数,这时要肯定孩子的想法,并引导学生会用一个式子表示(抓住定义就行了)
四.日历问题
1.观察2011年9月的日历,同一横行上相邻的3个数之间有什么关系?
日 一 二 三 四 五 六
1 2 3
4 5 6 7 8 9 10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30
2. 观察日历,同一竖列上相邻3个数之间有什么关系?
日 一 二 三 四 五 六
1 2 3
4 5 6 7 8 9 10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30
3.观察日历上用方框任意圈出的4个数,你能说出这4个数之间有什么关系吗?
日 一 二 三 四 五 六
1 2 3
4 5 6 7 8 9 10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30
五.随堂练习
用字母表示数——随堂练习
姓名: 评价:共10个空正确的有_____个空
1.一位同学的第二次的测验评价比第一次的进步了10分,若他第二次的评价为a分,那么他第一次的评价为 ______分.
2.某学校的学生共有x人,其中男生占52%,则男生人数为_______,女生人数为______.
3.若a表示三角形的底边的长,h表示三角形的高,S表示这个三角形的面积,则这个三角形的面积公式为 ____ ___.
4.“减去一个数等于加上这个数的相反数”这句话用字母可以表示为:
____ ___.
5.用字母表示三个连续整数: 、 、 .
6.下面为某年某月的月历。观察下列表格,并回答问题:
日 一 二 三 四 五 六
a
b x c
d
请你把a,b,c,d分别用x表示出来:a=_ ___,b=__ __,c=__ __,d=___ __.
参考答案:
1.(a-10);2. 52%x,(1-52%)x或者48%x;3. ;4.a-b=a+(﹣b);
5.a-1、a、a+1;或者a、a+1、a+2;或者a-2、a-1、a;
6. x-7、x-1、x+1;x+7。
六.课堂小结.
1.课堂知识小结
2.布置作业:课本第59页习题2.1,阅读材料。
3.课外阅读材料
课外阅读材料——用字母表示数五注意
1.注意字母具有一般性
用字母可以表示我们已经学过的任意一个有理数,同时随着我们所学知识的深入与需要,数的范围将进一步扩大,字母可以表示今后我们所学到的任何一个数,初学用字母表示数时,同学们一定要深刻理解用字母表示数的这种一般性.比如,字母可以表示正数、负数、零,同学们不要见到就认为是正数,见到–就认为是负数,见到2就认为一定比大,这是对字母表示数的一种极为错误的认识,实际上,不一定就是正数,–不一定就是负数, 2不一定就比大,这要看字母具体代表什么数,当=-2时,-=2,2=-4,即是一个负数,–就是正数, 2反而比要小.
2.注意字母的确定性
它表现在两个方面:一方面是指在同一个问题中,同一个字母只能表示同一个量,不同数量要用不同的字母来表示.比如在同分母分数的加法法则中,虽然、、均表示任意数,但在此等式中,等式两边的、、必须是分别表示同一个数量,即表示相同的分母, 、分别表示两个同分母分数的分子,同样的道理,我们也不能把相同的分母和两个分子用同一个字母来表示;另一方面,在用字母表示数时,一旦式子中的字母的取值确定了,式子的值也就随之确定了,如在圆的周长公式中,如果,那么这个圆的周长就是了.
3.注意字母的不确定性
同一个式子可以表示多种实际问题中的数量关系,如:式子可以表示:“每斤苹果元,买3斤苹果共需3元”,也可以表示:“每枝铅笔元,买3枝铅笔共需3元”等.
4.注意字母的限制性
用字母表示实际问题中的某一个数量时,字母的取值必须使这个问题有意义且符合实际,如“若某型号计算机的单价为元/台,则买台共需元”,这里只能表示正数,只能表示0和正整数.
5.注意字母的抽象性
要逐步理解和接受有些问题的结果可能就是一个用字母表示的式子,如,我们已经习惯于计算“若每小时行30千米,则2小时就会行30×2=60千米”这样的具体结果,因为我们可以想象的到60千米大概有多远.如果换成“若每小时行30千米,则小时就会行30千米”,这样的抽象结果,初学时,有的同学很难接受,因为我们想象不到30千米大概有多远.其实,学习了用字母表示数以后,像30或等这些用字母表示的数,完全可以作为一个结果.
同课章节目录
