反比例函数的图象与性质
图片预览






文档简介
(共24张PPT)
设计:谢彦文
制作:谢彦文
单位:桥头河镇株木中学
1. 反比例函数的定义:
3. 反比例函数的确定:
4.它的三种常见的表达形式:
2. 反比例函数的特征:
的函数,叫做反比例函数.
形如
k ≠0, x ≠0. x是-1次
待定系数法.
xy = k(k ≠ 0)
y=kx-1(k≠0)
说一说
(1)y = 3x-1
(2)y = 2x2
2.已知△ABC的面积为12,则△ABC的高h与它的底边a的函数关系式为
说一说
1.下列函数中哪些是反比例函数?
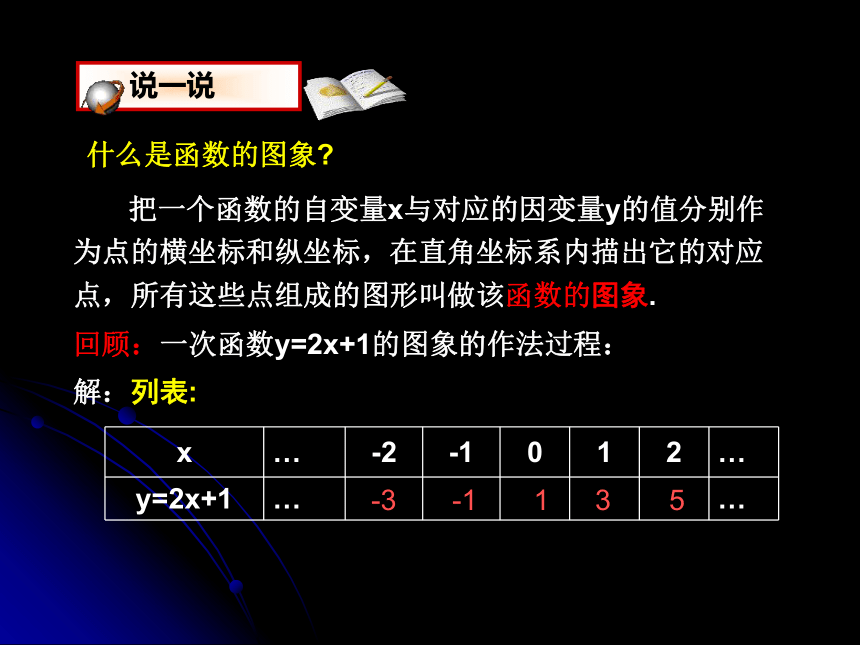
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象.
回顾:一次函数y=2x+1的图象的作法过程:
解:列表:
x … -2 -1 0 1 2 …
y=2x+1 … …
-3
-1
1
3
5
说一说
什么是函数的图象
y
x
3
0
2
1
-1
-2
-3
-1
-2
-3
1
2
3
4
5
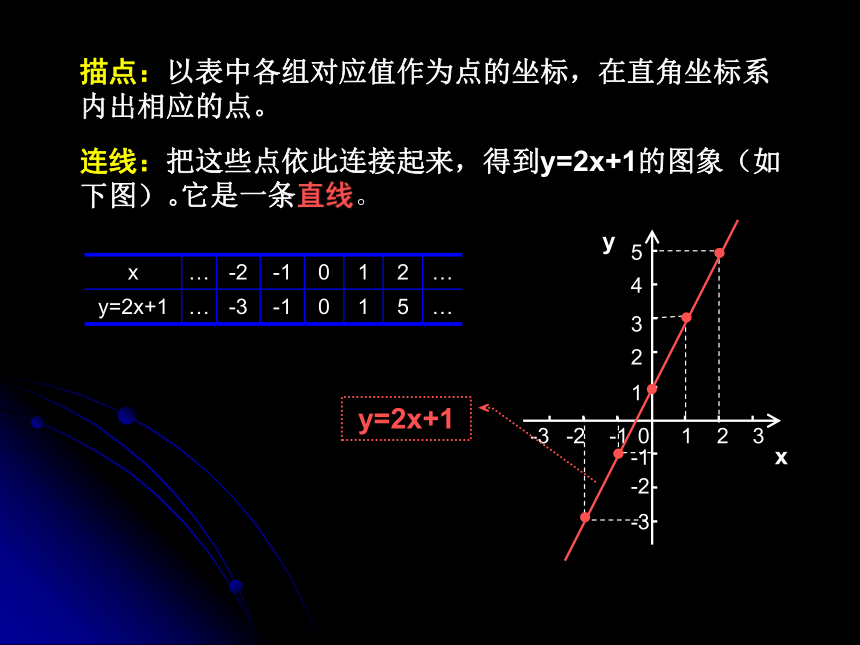
描点:以表中各组对应值作为点的坐标,在直角坐标系内出相应的点。
连线:把这些点依此连接起来,得到y=2x+1的图象(如下图)。
y=2x+1
它是一条直线。
x … -2 -1 0 1 2 …
y=2x+1 … -3 -1 0 1 5 …
函数图象画法
列
表
描
点
连
线
描点法
作函数图象的一般步骤是怎样的呢
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).
说一说
“心动”不如行动
动手体验
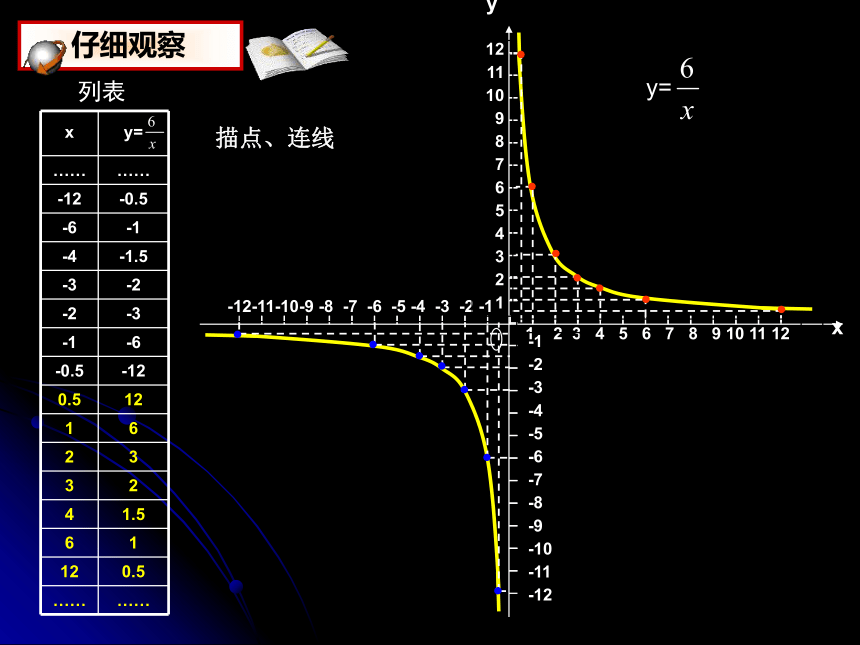
在直角坐标系中画出反比例函数 y= 的图象
x y=
…… ……
-12 -0.5
-6 -1
-4 -1.5
-3 -2
-2 -3
-1 -6
-0.5 -12
0.5 12
1 6
2 3
3 2
4 1.5
6 1
12 0.5
…… ……
列表
描点、连线
1 2 3 4 5 6 7 8 9 10 11 12
-12-11-10-9 -8 -7 -6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
-11
-12
12
11
10
9
8
7
6
5
4
3
2
1
x
y
y=
仔细观察
反比例函数的图象是由两个分支组成的,因此称反比例函数的图象为双曲线。
理解概念
从画反比例函数图象看,描点法还应注意什么
反比例函数图象画法步骤
列
表
描
点
连
线
描点法
注意:①列 x与y的对应值表时,X的值不能为零,但仍可以零为基数,左右均匀、对称地取值。
注意:②描点时自左住右用光滑曲线顺次连结,切忌用折线。
注意: ③两个分支合起来才是反比例函数图象。
注意: ④在列表时,自变量的值可以选取绝对值相等而符号相反的一对一对的数值,这样既可简化计算,又便于描点;列表、描点时,要尽量多取一些点,这样方便连线;描点时一定要养成按自变量从小到大的顺序依次画线, 从中体会函数的增减性;连线时必须用光滑的曲线连接各点; 曲线的发展趋势只能靠近坐标轴,而不能和坐标轴相交.
“心动”不如行动
函数图象画法
列
表
描
点
连
线
描点法
在同一直角坐标系内画出反比例函数 和 的函数图象。
动手操作
2. 反比例函数 的图象在哪两个象限?由
什么确定?
3. 反比例函数 具有怎样的对称性?
4. 反比例函数 的图象的变化趋势是怎样的,
它和两条坐标轴的位置关系是怎样的?
反比例函数 和 的图象在哪两个
象限?它们相同吗?
x
y
0
x
y
0
议一议
1.当k>0时,图象的两个分支分别在第一、三象限内;
2.当k<0时,图象的两个分支分别在第二、四象限内。
y =
x
6
x
y
0
y
x
y
x
6
y =
0
3.图象的两个分支关于直角坐标系的原点成中心对称。
x
0
如果知道双曲线的一支,利用对称性,如何画另一支?
4.双曲线无限接近于x、y轴,但永远不会与坐标轴相交
函数的性质
1、下列函数图像中,属于反比例函数图像的是( )
随堂练习
D
2、函数y=mxm的图象是双曲线,则m的值是( ) A -1 B 0 C 1 D 2
A
3、如果反比例函数y= 的图象在第一、三象限,
那么m的取值范围是___
随堂练习
m>
1
2
4、若反比例函数y= 的图象在第二、四象限,则直
线y=kx-3不经过第__ 象限
一
D
思维训练1
若 ,则函数 与 在同一平面直角坐标系中的图象大致是( )
思维训练2
B
思考题1
若点(-2,y1)、(-1,y2)(1,y3)都在反比例函数
y= 的图象上,则下列结论正确的是( )
A y1>y2>y3 B y2>y1>y3
C y3>y1>y2 D y3>y2>y1
B
思考题2
若点(-2,y1)、(-1,y2)(1,y3)都在反比例函数y= (m>0)的图象上,则下列结论正确的是( )
A y1>y2>y3 B y2>y1>y3
C y3>y1>y2 D y3>y2>y1
C
课后作业
在同一直角坐标系内画出反比例函数 和 的函数图象。
函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.
结束寄语
设计:谢彦文
制作:谢彦文
单位:桥头河镇株木中学
1. 反比例函数的定义:
3. 反比例函数的确定:
4.它的三种常见的表达形式:
2. 反比例函数的特征:
的函数,叫做反比例函数.
形如
k ≠0, x ≠0. x是-1次
待定系数法.
xy = k(k ≠ 0)
y=kx-1(k≠0)
说一说
(1)y = 3x-1
(2)y = 2x2
2.已知△ABC的面积为12,则△ABC的高h与它的底边a的函数关系式为
说一说
1.下列函数中哪些是反比例函数?
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象.
回顾:一次函数y=2x+1的图象的作法过程:
解:列表:
x … -2 -1 0 1 2 …
y=2x+1 … …
-3
-1
1
3
5
说一说
什么是函数的图象
y
x
3
0
2
1
-1
-2
-3
-1
-2
-3
1
2
3
4
5
描点:以表中各组对应值作为点的坐标,在直角坐标系内出相应的点。
连线:把这些点依此连接起来,得到y=2x+1的图象(如下图)。
y=2x+1
它是一条直线。
x … -2 -1 0 1 2 …
y=2x+1 … -3 -1 0 1 5 …
函数图象画法
列
表
描
点
连
线
描点法
作函数图象的一般步骤是怎样的呢
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).
说一说
“心动”不如行动
动手体验
在直角坐标系中画出反比例函数 y= 的图象
x y=
…… ……
-12 -0.5
-6 -1
-4 -1.5
-3 -2
-2 -3
-1 -6
-0.5 -12
0.5 12
1 6
2 3
3 2
4 1.5
6 1
12 0.5
…… ……
列表
描点、连线
1 2 3 4 5 6 7 8 9 10 11 12
-12-11-10-9 -8 -7 -6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
-11
-12
12
11
10
9
8
7
6
5
4
3
2
1
x
y
y=
仔细观察
反比例函数的图象是由两个分支组成的,因此称反比例函数的图象为双曲线。
理解概念
从画反比例函数图象看,描点法还应注意什么
反比例函数图象画法步骤
列
表
描
点
连
线
描点法
注意:①列 x与y的对应值表时,X的值不能为零,但仍可以零为基数,左右均匀、对称地取值。
注意:②描点时自左住右用光滑曲线顺次连结,切忌用折线。
注意: ③两个分支合起来才是反比例函数图象。
注意: ④在列表时,自变量的值可以选取绝对值相等而符号相反的一对一对的数值,这样既可简化计算,又便于描点;列表、描点时,要尽量多取一些点,这样方便连线;描点时一定要养成按自变量从小到大的顺序依次画线, 从中体会函数的增减性;连线时必须用光滑的曲线连接各点; 曲线的发展趋势只能靠近坐标轴,而不能和坐标轴相交.
“心动”不如行动
函数图象画法
列
表
描
点
连
线
描点法
在同一直角坐标系内画出反比例函数 和 的函数图象。
动手操作
2. 反比例函数 的图象在哪两个象限?由
什么确定?
3. 反比例函数 具有怎样的对称性?
4. 反比例函数 的图象的变化趋势是怎样的,
它和两条坐标轴的位置关系是怎样的?
反比例函数 和 的图象在哪两个
象限?它们相同吗?
x
y
0
x
y
0
议一议
1.当k>0时,图象的两个分支分别在第一、三象限内;
2.当k<0时,图象的两个分支分别在第二、四象限内。
y =
x
6
x
y
0
y
x
y
x
6
y =
0
3.图象的两个分支关于直角坐标系的原点成中心对称。
x
0
如果知道双曲线的一支,利用对称性,如何画另一支?
4.双曲线无限接近于x、y轴,但永远不会与坐标轴相交
函数的性质
1、下列函数图像中,属于反比例函数图像的是( )
随堂练习
D
2、函数y=mxm的图象是双曲线,则m的值是( ) A -1 B 0 C 1 D 2
A
3、如果反比例函数y= 的图象在第一、三象限,
那么m的取值范围是___
随堂练习
m>
1
2
4、若反比例函数y= 的图象在第二、四象限,则直
线y=kx-3不经过第__ 象限
一
D
思维训练1
若 ,则函数 与 在同一平面直角坐标系中的图象大致是( )
思维训练2
B
思考题1
若点(-2,y1)、(-1,y2)(1,y3)都在反比例函数
y= 的图象上,则下列结论正确的是( )
A y1>y2>y3 B y2>y1>y3
C y3>y1>y2 D y3>y2>y1
B
思考题2
若点(-2,y1)、(-1,y2)(1,y3)都在反比例函数y= (m>0)的图象上,则下列结论正确的是( )
A y1>y2>y3 B y2>y1>y3
C y3>y1>y2 D y3>y2>y1
C
课后作业
在同一直角坐标系内画出反比例函数 和 的函数图象。
函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.
结束寄语
