人教版八年级数学上学期 同步练习: 13.2 画轴对称图形(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上学期 同步练习: 13.2 画轴对称图形(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 197.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-14 23:37:27 | ||
图片预览


文档简介
13.2 画轴对称图形
一.填空题
1.在平面直角坐标系中,点A(a,﹣3)向左平移3个单位得点A′,若点A和A′关于y轴对称,则a= .
2.已知点P(﹣1,2),那么点P关于直线x=1的对称点Q的坐标是 .
3.如图,在平面直角坐标系中,已知点A的坐标为(4,4),若△ABC是关于直线y=1的轴对称图形,则点B的坐标为 ;若△ABC是关于直线y=a的轴对称图形,则点B的坐标为 .
4.若P关于x轴的对称点为(3,a),关于y轴对称的点为(b,2),则P点的坐标为 .
5.已知点A(a,2),B(﹣3,b)关于y轴对称,则ab= .
6.若点P(3,﹣1)关于y轴的对称点Q的坐标是(a+b,1﹣b),则ab的值为 .
7.如果A(a﹣1,3),A′(4,b﹣2)关于x轴对称,则a= ,b= .
8.已知P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,则(a+b)2019的值为 .
9.如图,在平面直角坐标系中,一颗棋子从点P(0,﹣2)处开始依次关于点A(﹣1,﹣1),B(1,2),C(2,1)作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…,如此下去.则经过第2011次跳动之后,棋子落点的坐标为 .
10.已知P1点关于x轴的对称点P2(3﹣2a,2a﹣5)是第三象限内的整点(横、纵坐标都为整数的点,称为整点),则P1点的坐标是 .
二.解答题
11.在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)顶点A关于x轴对称的点的坐标A'( , ),顶点C先向右平移3个单位,再向下平移2个单位后的坐标C'( , );
(2)将△ABC的纵坐标保持不变,横坐标分别乘﹣1得△DEF,请你直接画出图形;
(3)在平面直角坐标系xOy中有一点P,使得△ABC与△PBC全等,这样的P点有 个.(A点除外)
12.在直角坐标系中,△ABC的顶点坐标如图所示,
(1)请你在图中先作出△ABC关于直线m(直线m上点的横坐标均为﹣1)对称图形△A1B1C1,再作出△A1B1C1关于直线n(直线n上点的纵坐标均为2)对称图形△A2B2C2;
(2)线段BC上有一点M(a,b),点M关于直线m的对称点为N,点N关于直线的n的对称点为E,求N、E的坐标(用含a,b的代数式表示).
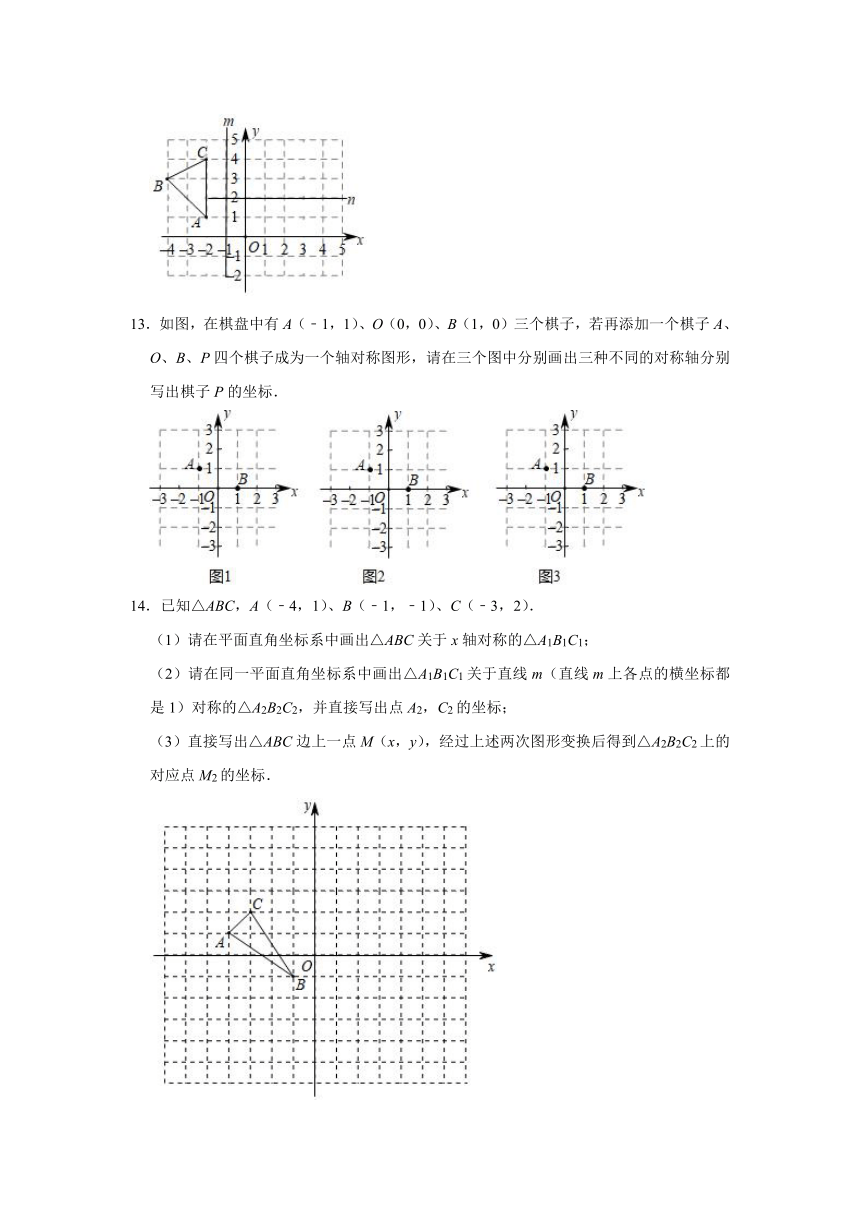
13.如图,在棋盘中有A(﹣1,1)、O(0,0)、B(1,0)三个棋子,若再添加一个棋子A、O、B、P四个棋子成为一个轴对称图形,请在三个图中分别画出三种不同的对称轴分别写出棋子P的坐标.
14.已知△ABC,A(﹣4,1)、B(﹣1,﹣1)、C(﹣3,2).
(1)请在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)请在同一平面直角坐标系中画出△A1B1C1关于直线m(直线m上各点的横坐标都是1)对称的△A2B2C2,并直接写出点A2,C2的坐标;
(3)直接写出△ABC边上一点M(x,y),经过上述两次图形变换后得到△A2B2C2上的对应点M2的坐标.
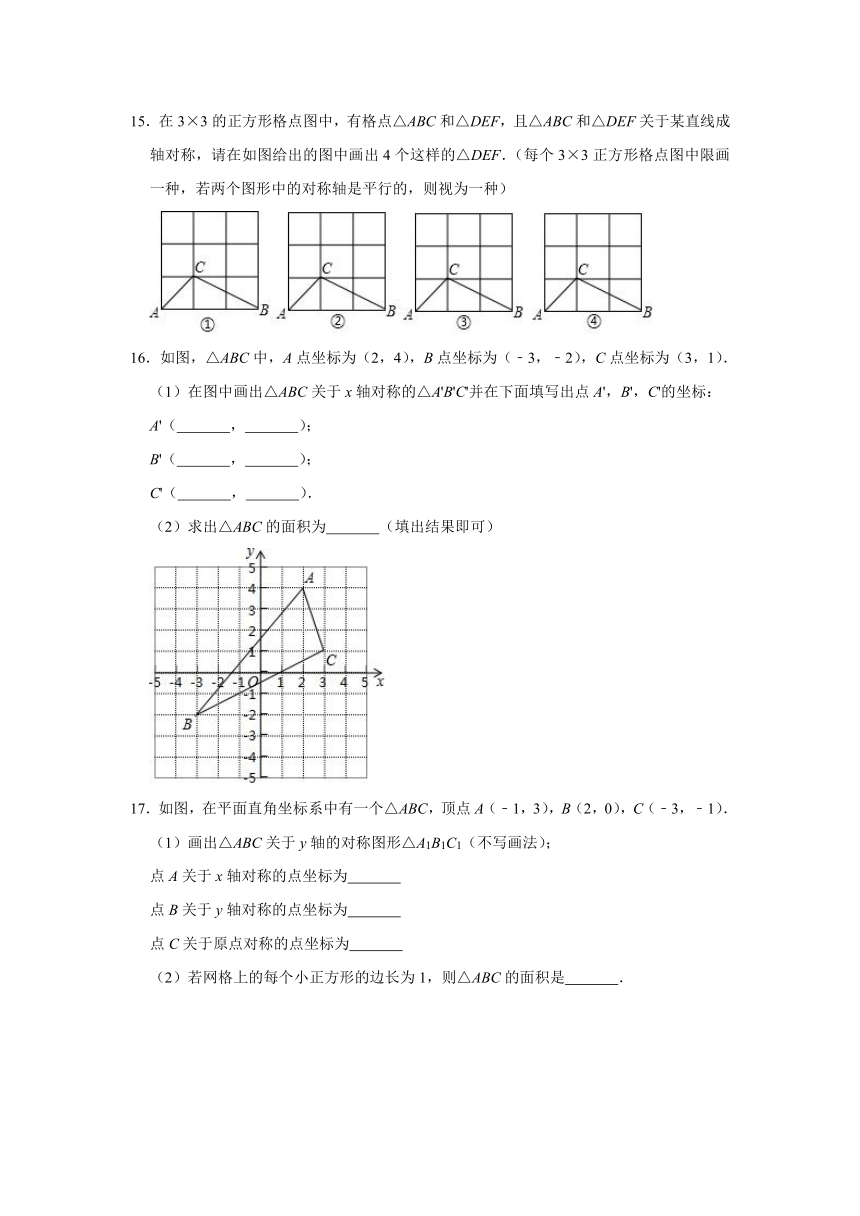
15.在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在如图给出的图中画出4个这样的△DEF.(每个3×3正方形格点图中限画一种,若两个图形中的对称轴是平行的,则视为一种)
16.如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).
(1)在图中画出△ABC关于x轴对称的△A'B'C'并在下面填写出点A',B',C'的坐标:
A'( , );
B'( , );
C'( , ).
(2)求出△ABC的面积为 (填出结果即可)
17.如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .
参考答案
一.填空题
1. 1.5.
2.(3,2).
3.(4,﹣2),(4,2a﹣4).
4.(3,2).
5.6.
6.﹣10.
7. a=5,b=﹣1.
8.﹣1.
9.(﹣2,0).
10.(﹣1,1).
二.解答题
11.解:(1)∵A(﹣4,3),C(﹣2,5),
∴A′(﹣4,﹣3),C'(1,3);
故答案为:﹣4,﹣3;1,3;
(2)如图所示:即为所求;
(3)△ABC与△PBC全等,这样的P点有3个.
故答案为:3.
12.解:(1)如图所示,△A1B1C1,△A2B2C2即为所求;
(2)设点N的坐标为(x,y),点E的坐标为(p,q),
∵点M与点N关于直线m对称,
∴=﹣1,y=b,
解得x=﹣2﹣a,y=b,
∴点N的坐标为(﹣2﹣a,b),
又∵点N与点E关于直线n对称,
∴p=﹣2﹣a,=2,
解得p=﹣2﹣a,q=4﹣b,
∴点E的坐标为(﹣2﹣a,4﹣b).
13.解:如图所示,棋子P的坐标分别为(﹣1,﹣1),(2,1),(0,﹣1),(﹣1,2).(答案不唯一)
14.解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求,点A2,C2的坐标分别为(6,﹣1)和(5,﹣2);
(3)点M(x,y)关于x轴对称的点M1的坐标为(x,﹣y),点M1关于直线m对称的点M2的坐标为(﹣x+2,﹣y).
∴经过上述两次图形变换后得到△A2B2C2上的对应点M2的坐标为(﹣x+2,﹣y).
15.解:如图,△DEF即为所求.(答案不唯一)
16.解:(1)如图所示,△A'B'C'即为所求:
由图可得:A'(2,﹣4);B'(﹣3,2);C'(3,﹣1).
故答案为:2,﹣4;﹣3,2;3,﹣1.
(2)△ABC的面积为:6×6﹣×1×3﹣×3×6﹣×5×6=36﹣﹣9﹣15=10.
故答案为:10.
17.解:(1)点A关于x轴对称的点坐标为 (﹣1,﹣3);
点B关于y轴对称的点坐标为:(﹣2,0);
点C关于原点对称的点坐标为:(3,1);
故答案为:(﹣1,﹣3),(﹣2,0),(3,1);
(2)△ABC的面积是:4×5﹣×2×4﹣×3×3﹣×1×5=9.
故答案为:9.
一.填空题
1.在平面直角坐标系中,点A(a,﹣3)向左平移3个单位得点A′,若点A和A′关于y轴对称,则a= .
2.已知点P(﹣1,2),那么点P关于直线x=1的对称点Q的坐标是 .
3.如图,在平面直角坐标系中,已知点A的坐标为(4,4),若△ABC是关于直线y=1的轴对称图形,则点B的坐标为 ;若△ABC是关于直线y=a的轴对称图形,则点B的坐标为 .
4.若P关于x轴的对称点为(3,a),关于y轴对称的点为(b,2),则P点的坐标为 .
5.已知点A(a,2),B(﹣3,b)关于y轴对称,则ab= .
6.若点P(3,﹣1)关于y轴的对称点Q的坐标是(a+b,1﹣b),则ab的值为 .
7.如果A(a﹣1,3),A′(4,b﹣2)关于x轴对称,则a= ,b= .
8.已知P1(a﹣1,5)和P2(2,b﹣1)关于x轴对称,则(a+b)2019的值为 .
9.如图,在平面直角坐标系中,一颗棋子从点P(0,﹣2)处开始依次关于点A(﹣1,﹣1),B(1,2),C(2,1)作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…,如此下去.则经过第2011次跳动之后,棋子落点的坐标为 .
10.已知P1点关于x轴的对称点P2(3﹣2a,2a﹣5)是第三象限内的整点(横、纵坐标都为整数的点,称为整点),则P1点的坐标是 .
二.解答题
11.在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)顶点A关于x轴对称的点的坐标A'( , ),顶点C先向右平移3个单位,再向下平移2个单位后的坐标C'( , );
(2)将△ABC的纵坐标保持不变,横坐标分别乘﹣1得△DEF,请你直接画出图形;
(3)在平面直角坐标系xOy中有一点P,使得△ABC与△PBC全等,这样的P点有 个.(A点除外)
12.在直角坐标系中,△ABC的顶点坐标如图所示,
(1)请你在图中先作出△ABC关于直线m(直线m上点的横坐标均为﹣1)对称图形△A1B1C1,再作出△A1B1C1关于直线n(直线n上点的纵坐标均为2)对称图形△A2B2C2;
(2)线段BC上有一点M(a,b),点M关于直线m的对称点为N,点N关于直线的n的对称点为E,求N、E的坐标(用含a,b的代数式表示).
13.如图,在棋盘中有A(﹣1,1)、O(0,0)、B(1,0)三个棋子,若再添加一个棋子A、O、B、P四个棋子成为一个轴对称图形,请在三个图中分别画出三种不同的对称轴分别写出棋子P的坐标.
14.已知△ABC,A(﹣4,1)、B(﹣1,﹣1)、C(﹣3,2).
(1)请在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)请在同一平面直角坐标系中画出△A1B1C1关于直线m(直线m上各点的横坐标都是1)对称的△A2B2C2,并直接写出点A2,C2的坐标;
(3)直接写出△ABC边上一点M(x,y),经过上述两次图形变换后得到△A2B2C2上的对应点M2的坐标.
15.在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在如图给出的图中画出4个这样的△DEF.(每个3×3正方形格点图中限画一种,若两个图形中的对称轴是平行的,则视为一种)
16.如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).
(1)在图中画出△ABC关于x轴对称的△A'B'C'并在下面填写出点A',B',C'的坐标:
A'( , );
B'( , );
C'( , ).
(2)求出△ABC的面积为 (填出结果即可)
17.如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .
参考答案
一.填空题
1. 1.5.
2.(3,2).
3.(4,﹣2),(4,2a﹣4).
4.(3,2).
5.6.
6.﹣10.
7. a=5,b=﹣1.
8.﹣1.
9.(﹣2,0).
10.(﹣1,1).
二.解答题
11.解:(1)∵A(﹣4,3),C(﹣2,5),
∴A′(﹣4,﹣3),C'(1,3);
故答案为:﹣4,﹣3;1,3;
(2)如图所示:即为所求;
(3)△ABC与△PBC全等,这样的P点有3个.
故答案为:3.
12.解:(1)如图所示,△A1B1C1,△A2B2C2即为所求;
(2)设点N的坐标为(x,y),点E的坐标为(p,q),
∵点M与点N关于直线m对称,
∴=﹣1,y=b,
解得x=﹣2﹣a,y=b,
∴点N的坐标为(﹣2﹣a,b),
又∵点N与点E关于直线n对称,
∴p=﹣2﹣a,=2,
解得p=﹣2﹣a,q=4﹣b,
∴点E的坐标为(﹣2﹣a,4﹣b).
13.解:如图所示,棋子P的坐标分别为(﹣1,﹣1),(2,1),(0,﹣1),(﹣1,2).(答案不唯一)
14.解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求,点A2,C2的坐标分别为(6,﹣1)和(5,﹣2);
(3)点M(x,y)关于x轴对称的点M1的坐标为(x,﹣y),点M1关于直线m对称的点M2的坐标为(﹣x+2,﹣y).
∴经过上述两次图形变换后得到△A2B2C2上的对应点M2的坐标为(﹣x+2,﹣y).
15.解:如图,△DEF即为所求.(答案不唯一)
16.解:(1)如图所示,△A'B'C'即为所求:
由图可得:A'(2,﹣4);B'(﹣3,2);C'(3,﹣1).
故答案为:2,﹣4;﹣3,2;3,﹣1.
(2)△ABC的面积为:6×6﹣×1×3﹣×3×6﹣×5×6=36﹣﹣9﹣15=10.
故答案为:10.
17.解:(1)点A关于x轴对称的点坐标为 (﹣1,﹣3);
点B关于y轴对称的点坐标为:(﹣2,0);
点C关于原点对称的点坐标为:(3,1);
故答案为:(﹣1,﹣3),(﹣2,0),(3,1);
(2)△ABC的面积是:4×5﹣×2×4﹣×3×3﹣×1×5=9.
故答案为:9.
