导数的应用
图片预览




文档简介
(共12张PPT)
导数的应用
一、学习目标
1.会用导数求函数的单调区间或者判断函数
的单调性.
2.会用导数求函数给定区间上的极值和最值.
二、诊断补偿
2.思考:利用导数可以解决哪些问题?
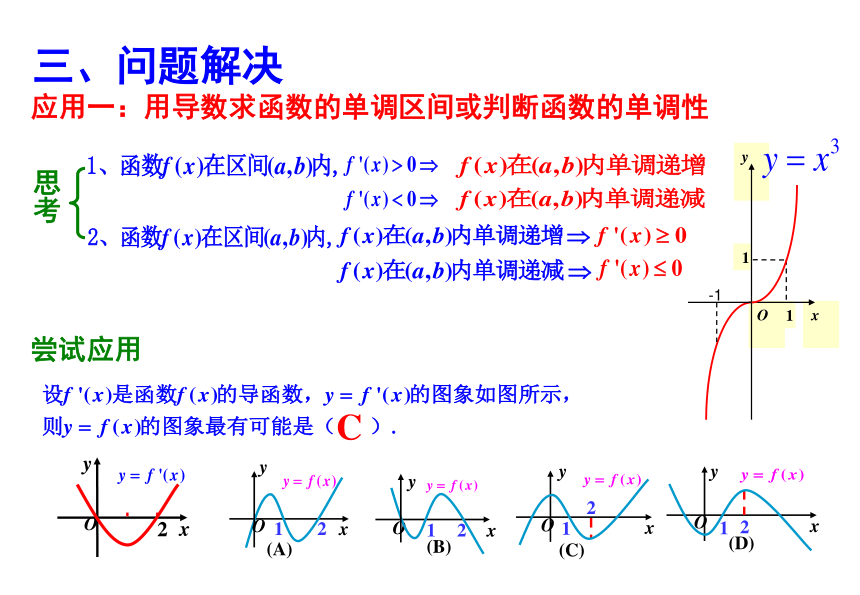
三、问题解决
应用一:用导数求函数的单调区间或判断函数的单调性
思考
尝试应用
x
y
O
2
y
x
1
2
(A)
O
x
y
O
1
2
(B)
x
y
O
1
2
(C)
x
y
O
1
2
(D)
C
O
x
1
1
y
-1
典例析与练
x
y
o
跟踪练习:
两个单调区间之间
要用“,”或“和”连接
易
错
点
B
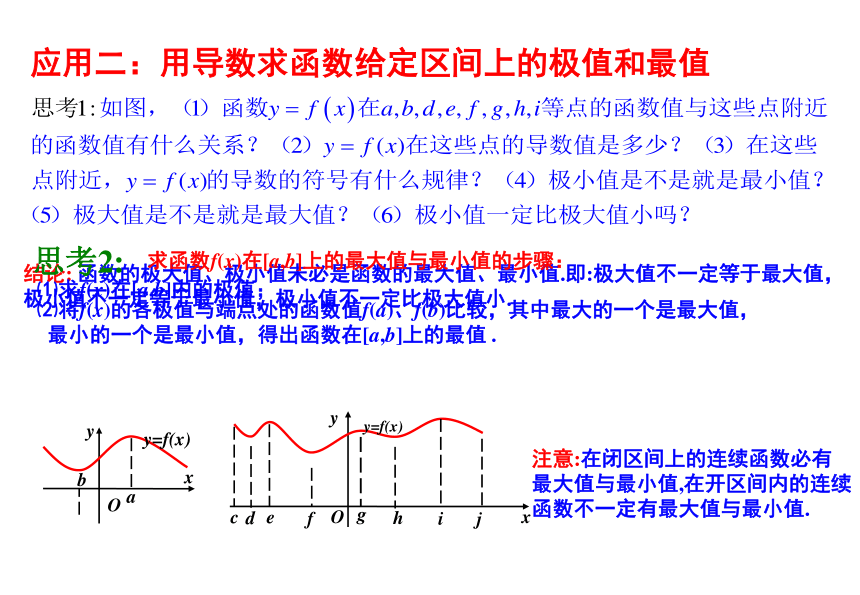
应用二:用导数求函数给定区间上的极值和最值
c
d
e
f
O
g
h
i
j
x
y
y=f(x)
b
a
y=f(x)
y
x
O
结论: 函数的极大值、极小值未必是函数的最大值、最小值.即:极大值不一定等于最大值,极小值不一定等于最小值,极小值不一定比极大值小.
⑵将f(x)的各极值与端点处的函数值f(a)、f(b)比较,其中最大的一个是最大值,
最小的一个是最小值,得出函数在[a,b]上的最值 .
思考2:
求函数f(x)在[a,b]上的最大值与最小值的步骤:
⑴求f(x)在[a,b]内的极值;
注意:在闭区间上的连续函数必有最大值与最小值,在开区间内的连续函数不一定有最大值与最小值.
典例析与练
x -3 (-3,-2) -2 ( ,1) 1
+ 0 - 0 +
y 8 单调递增 13 单调递减 单调递增 4
∴ y=f(x)在[-3,1]上的最大值为13,最小值为
跟踪练习:
①
四、能力提高
2.以下四图,都是同一坐标系中三次函数及其导函数的图象,其中一定不正确的序号是 ( )
A.①、② B.①、③ C.③、④ D.①、④
C
D
A
S(千米)
t(小时)
O
1
3
五、知识网络构建
导数
有导数的函数的极值的求法
有导数的函数的最值的求法
极值
端点值
实际问题
六、分层作业
(一)基础作业:
(二)能力作业:
导数的应用
一、学习目标
1.会用导数求函数的单调区间或者判断函数
的单调性.
2.会用导数求函数给定区间上的极值和最值.
二、诊断补偿
2.思考:利用导数可以解决哪些问题?
三、问题解决
应用一:用导数求函数的单调区间或判断函数的单调性
思考
尝试应用
x
y
O
2
y
x
1
2
(A)
O
x
y
O
1
2
(B)
x
y
O
1
2
(C)
x
y
O
1
2
(D)
C
O
x
1
1
y
-1
典例析与练
x
y
o
跟踪练习:
两个单调区间之间
要用“,”或“和”连接
易
错
点
B
应用二:用导数求函数给定区间上的极值和最值
c
d
e
f
O
g
h
i
j
x
y
y=f(x)
b
a
y=f(x)
y
x
O
结论: 函数的极大值、极小值未必是函数的最大值、最小值.即:极大值不一定等于最大值,极小值不一定等于最小值,极小值不一定比极大值小.
⑵将f(x)的各极值与端点处的函数值f(a)、f(b)比较,其中最大的一个是最大值,
最小的一个是最小值,得出函数在[a,b]上的最值 .
思考2:
求函数f(x)在[a,b]上的最大值与最小值的步骤:
⑴求f(x)在[a,b]内的极值;
注意:在闭区间上的连续函数必有最大值与最小值,在开区间内的连续函数不一定有最大值与最小值.
典例析与练
x -3 (-3,-2) -2 ( ,1) 1
+ 0 - 0 +
y 8 单调递增 13 单调递减 单调递增 4
∴ y=f(x)在[-3,1]上的最大值为13,最小值为
跟踪练习:
①
四、能力提高
2.以下四图,都是同一坐标系中三次函数及其导函数的图象,其中一定不正确的序号是 ( )
A.①、② B.①、③ C.③、④ D.①、④
C
D
A
S(千米)
t(小时)
O
1
3
五、知识网络构建
导数
有导数的函数的极值的求法
有导数的函数的最值的求法
极值
端点值
实际问题
六、分层作业
(一)基础作业:
(二)能力作业:
