2019-2020学年黑龙江省哈尔滨市南岗区萧红中学七年级下学期期中数学试卷(五四学制) (Word版 含解析)
文档属性
| 名称 | 2019-2020学年黑龙江省哈尔滨市南岗区萧红中学七年级下学期期中数学试卷(五四学制) (Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 950.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-15 05:42:20 | ||
图片预览




文档简介
2019-2020学年黑龙江省哈尔滨市南岗区萧红中学七年级第二学期期中数学试卷(五四学制)
一、选择题(共20小题).
1.(3分)下列方程中,属于二元一次方程的是( )
A.x+y﹣2=0 B.xy+1=﹣4 C.3x2+y=8 D.x﹣y﹣2z=10
2.(3分)已知a<b,则下列不等式中不正确的是( )
A.2a<2b B.﹣3a<﹣3b C.a+3<b+3 D.a﹣1<b﹣1
3.(3分)在数轴上表示不等式x≥﹣2的解集,正确的是( )
A. B.
C. D.
4.(3分)下列长度的三条线段能组成三角形的是( )
A.1,2,3 B.1,,3 C.3,4,8 D.4,5,6
5.(3分)下列图形不具有稳定性的是( )
A. B.
C. D.
6.(3分)一个多边形的外角和与它的内角和相等,则多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
7.(3分)如图,△ACE≌△DBF,若∠E=∠F,AD=8,BC=2,则AB等于( )
A.6 B.5 C.3 D.不能确定
8.(3分)如图,AD=AC,BD=BC,则△ABC≌△ABD的根据是( )
A.SSS B.ASA C.AAS D.SAS
9.(3分)一只笼子装有鸡和兔共有10个头,34只脚,每只鸡有两只脚,每只兔有四只脚.设鸡有x只,兔有y只,则可列二元一次方程组( )
A. B.
C. D.
10.(3分)下面命题:
(1)二元一次方程2x﹣3y=4的解有且只有一个;
(2)只有一条高在内部的三角形是钝角三角形;
(3)等腰三角形的周长是22,一边是10,那么另一边一定是6;
(4)有两边和一个角分别相等的两个三角形全等;
(5)x=6是x﹣7<0的解集.正确的个数有( )
A.0个 B.1个 C.2个 D.3个
11.(3分)已知4x﹣y=5,用x表示y,得y=( )
A.5﹣4x B.4x﹣5 C. D.
12.(3分)用不等式表示,x与5的差不大于x的2倍( )
A.x﹣5>2x B.x﹣5≥2x C.x﹣5≤2x D.x﹣5<2x
13.(3分)不等式组的整数解为( )
A.2<x≤5 B.5 C.3 D.3,4,5
14.(3分)已知方程组的解满足方程x+2y=k,则k=( )
A.4 B.﹣3 C.3 D.不能确定
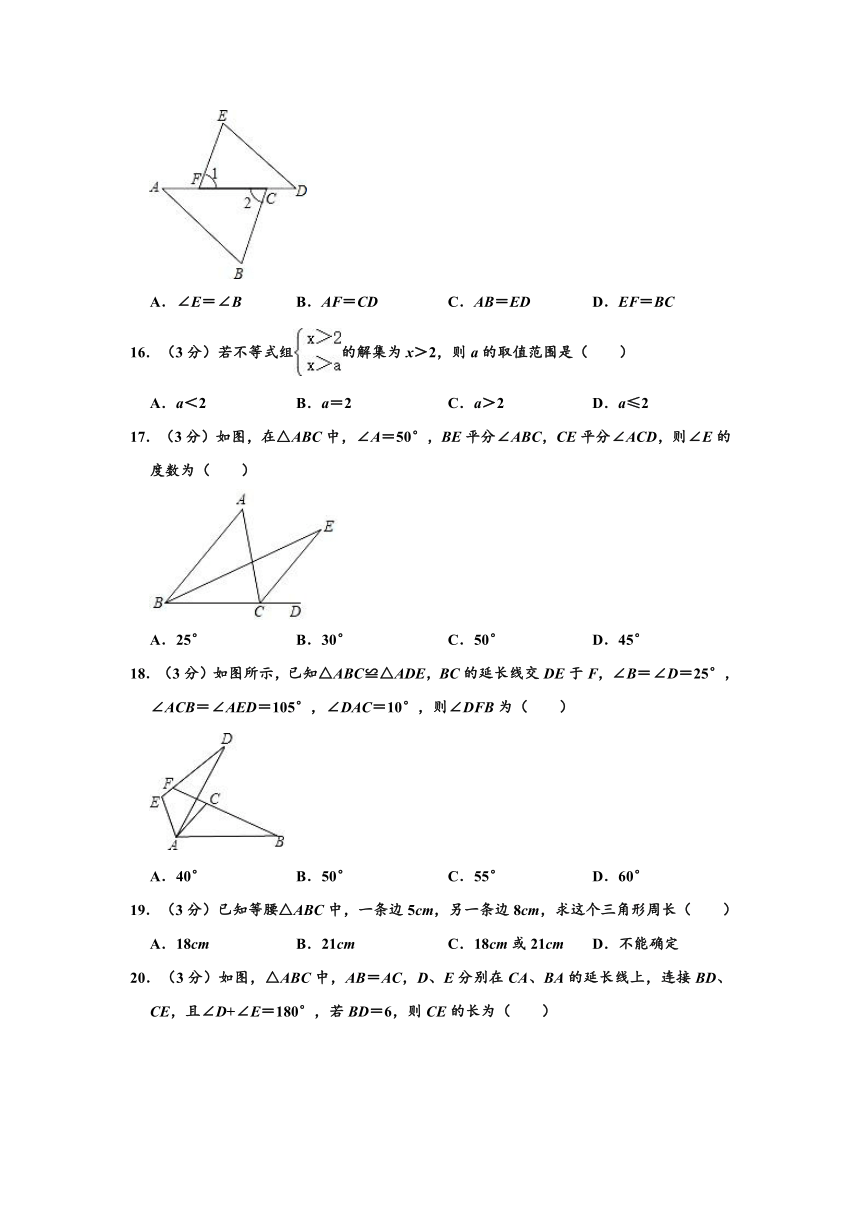
15.(3分)如图,∠A=∠D,∠1=∠2,则下面条件中添加后仍不能得到△ABC≌△DEF是( )
A.∠E=∠B B.AF=CD C.AB=ED D.EF=BC
16.(3分)若不等式组的解集为x>2,则a的取值范围是( )
A.a<2 B.a=2 C.a>2 D.a≤2
17.(3分)如图,在△ABC中,∠A=50°,BE平分∠ABC,CE平分∠ACD,则∠E的度数为( )
A.25° B.30° C.50° D.45°
18.(3分)如图所示,已知△ABC≌△ADE,BC的延长线交DE于F,∠B=∠D=25°,∠ACB=∠AED=105°,∠DAC=10°,则∠DFB为( )
A.40° B.50° C.55° D.60°
19.(3分)已知等腰△ABC中,一条边5cm,另一条边8cm,求这个三角形周长( )
A.18cm B.21cm C.18cm或21cm D.不能确定
20.(3分)如图,△ABC中,AB=AC,D、E分别在CA、BA的延长线上,连接BD、CE,且∠D+∠E=180°,若BD=6,则CE的长为( )
A.6 B.5 C.3 D.4.5
二、解答题(21,22,各8分,23题6分,24题8分,25,26,27各10分)
21.解方程组
(1);
(2).
22.解不等式
(1)5(x+2)≥1﹣2(x﹣1);
(2)解不等式组.
23.如图,方格纸中每个小正方形的边长均为1,线段AB的端点A,B均在小正方形的顶点上,请画出满足下面条件的图形,要求所画图形的各个顶点均在小正方形的顶点上.
(1)在图中画出面积为12的钝角△ABC,且满足∠A是钝角;
(2)请连接顶点,用一条线段将图中△ABC分成面积相等的两部分;
(3)请画出△ABC的高CD.
24.如图,AB=AC,BE=CD.
(1)求证:∠B=∠C;
(2)连接AO,若∠1=∠2,不添加任何辅助线,直接写出图中所有的全等三角形.
25.(10分)2020年是不寻常的一年,新冠肺炎充斥着我们的生活,病毒无情人有情,很多最美逆行者奔赴疫情的前线,不顾自己的安危令我们感动,哈市雷兵公司奔赴疫情前沿慰问医护人员,欲购进甲,乙两种呼吸机.若购进甲种2台,乙种3台,则共需要成本17000元;若购进甲种3台,乙种1台.则共需要成本15000元.
(1)求甲,乙两种呼吸机每台成本分别为多少元?
(2)该公司决定在成本不超过300000元的前提下购进甲、乙两种呼吸机.若购进乙种台数比甲种台数的3倍还多10台,求最多购进甲种呼吸机多少台?
26.(10分)已知:如图,四边形ABCD中,∠BAD=∠BCD,∠ABC+∠ADC=180°.
(1)如图1,求∠BCD的度数;
(2)如图2,若∠ACB=50°,∠BAE+∠DAC=∠DFC,求∠G的度数;
(3)如图3,在(2)的条件下,若AG=AC,S△ACD:S△ADG=3:7,2∠ADG+∠CDG=180°,DC=5,求DG的长.
27.(10分)如图.已知在平面直角坐标系中,△ABC的AB边经过原点O,AC交y轴于点D,且D是AC的中点,C(m,0),D(0,n),m.n满足.
(1)如图1,求OC和OD的长度;
(2)如图2,若E是线段CO上的一个动点,当S△AOE=S△AOD时,求E点的坐标;
(3)如图3,在(2)的条件下,若CO平分∠ACB,S△AOC=3S△BOC,求S△BDE.
参考答案
一、选择题(共20小题,每小题3分,满分60分)
1.(3分)下列方程中,属于二元一次方程的是( )
A.x+y﹣2=0 B.xy+1=﹣4 C.3x2+y=8 D.x﹣y﹣2z=10
解:A.x+y﹣2=0是含有两个未知数,且含未知数项的最高次数为一次的整式方程,是二元一次方程;
B.xy+1=﹣4中xy的次数为2,不是二元一次方程;
C.3x2+y=8中3x2的次数为2,不是二元一次方程;
D.x﹣y﹣2z=10中含有3个未知数,不是二元一次方程;
故选:A.
2.(3分)已知a<b,则下列不等式中不正确的是( )
A.2a<2b B.﹣3a<﹣3b C.a+3<b+3 D.a﹣1<b﹣1
解:由a<b得
A. 2a<2b,故选项正确;
B.﹣3a>﹣3b,故选项不正确;
C. a+3<b+3,故选项正确;
D. a﹣1<b﹣1,故选项正确;
故选:B.
3.(3分)在数轴上表示不等式x≥﹣2的解集,正确的是( )
A. B.
C. D.
解:∵不等式x≥﹣2中包含等于号,
∴必须用实心圆点,
∴可排除A、B,
∵不等式x≥﹣2中是大于等于,
∴折线应向右折,
∴可排除D.
故选:C.
4.(3分)下列长度的三条线段能组成三角形的是( )
A.1,2,3 B.1,,3 C.3,4,8 D.4,5,6
解:A、1+2=3,不能组成三角形,故本选项错误;
B、1+<3,不能组成三角形,故本选项错误;
C、3+4<8,不能组成三角形,故本选项错误;
D、4+5>6,能组成三角形,故本选项正确.
故选:D.
5.(3分)下列图形不具有稳定性的是( )
A. B.
C. D.
解:根据三角形的稳定性可得,B、C、D都具有稳定性.不具有稳定性的是A选项.
故选:A.
6.(3分)一个多边形的外角和与它的内角和相等,则多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
解:设多边形的边数为n.
根据题意得:(n﹣2)×180°=360°,
解得:n=4.
故选:B.
7.(3分)如图,△ACE≌△DBF,若∠E=∠F,AD=8,BC=2,则AB等于( )
A.6 B.5 C.3 D.不能确定
解:∵△ACE≌△DBF,∠E=∠F,AD=8,BC=2
∴AC=BD,即AB+BC=CD+BC
∴AB=CD
∴AB=(AD﹣BC)÷2=(8﹣2)÷2=3
故选:C.
8.(3分)如图,AD=AC,BD=BC,则△ABC≌△ABD的根据是( )
A.SSS B.ASA C.AAS D.SAS
解:在△ABC和ABD中,,
∴△ABC≌△ABD(SSS),
故选:A.
9.(3分)一只笼子装有鸡和兔共有10个头,34只脚,每只鸡有两只脚,每只兔有四只脚.设鸡有x只,兔有y只,则可列二元一次方程组( )
A. B.
C. D.
解:设鸡有x只,兔有y只,
依题意得.
故选:A.
10.(3分)下面命题:
(1)二元一次方程2x﹣3y=4的解有且只有一个;
(2)只有一条高在内部的三角形是钝角三角形;
(3)等腰三角形的周长是22,一边是10,那么另一边一定是6;
(4)有两边和一个角分别相等的两个三角形全等;
(5)x=6是x﹣7<0的解集.正确的个数有( )
A.0个 B.1个 C.2个 D.3个
解:(1)二元一次方程2x﹣3y=4的解有无数个,原命题是假命题;
(2)只有一条高在内部的三角形是直角三角形或钝角三角形,是假命题;
(3)等腰三角形的周长是22,一边是10,那么另一边是6或2,是假命题;
(4)有两边和其夹角分别相等的两个三角形全等,原命题是假命题;
(5)x=6是x﹣7<0的解,原命题是假命题;
故选:A.
11.(3分)已知4x﹣y=5,用x表示y,得y=( )
A.5﹣4x B.4x﹣5 C. D.
解:方程4x﹣y=5,
移项得:﹣y=5﹣4x,
解得:y=4x﹣5.
故选:B.
12.(3分)用不等式表示,x与5的差不大于x的2倍( )
A.x﹣5>2x B.x﹣5≥2x C.x﹣5≤2x D.x﹣5<2x
解:由题意得:x﹣5≤2x;
故选:C.
13.(3分)不等式组的整数解为( )
A.2<x≤5 B.5 C.3 D.3,4,5
解:,
由①得:x>2,
由②得:x≤5,
∴不等式组的解集是2<x≤5,
∴不等式组的整数解是3,4,5.
故选:D.
14.(3分)已知方程组的解满足方程x+2y=k,则k=( )
A.4 B.﹣3 C.3 D.不能确定
解:,
①+②得:3x=9,
解得:x=3,
把x=3代入②得;y=﹣3,
则k=x+2y=3﹣6=﹣3.
故选:B.
15.(3分)如图,∠A=∠D,∠1=∠2,则下面条件中添加后仍不能得到△ABC≌△DEF是( )
A.∠E=∠B B.AF=CD C.AB=ED D.EF=BC
解:A、根据∠A=∠D,∠1=∠2和∠E=∠B不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项符合题意;
B、∵AF=CD,
∴AF+FC=CD+FC,
即AC=DF,
在△ABC和△DEF中
∴△ABC≌△DEF(ASA),故本选项不符合题意;
C、在△ABC和△DEF中
∴△ABC≌△DEF(AAS),故本选项不符合题意;
D、在△ABC和△DEF中
∴△ABC≌△DEF(AAS),故本选项不符合题意;
故选:A.
16.(3分)若不等式组的解集为x>2,则a的取值范围是( )
A.a<2 B.a=2 C.a>2 D.a≤2
解:因为不等式组的解集为x>2,根据同大取大的原则可知2≥a,故选D.
17.(3分)如图,在△ABC中,∠A=50°,BE平分∠ABC,CE平分∠ACD,则∠E的度数为( )
A.25° B.30° C.50° D.45°
解:∵∠ACD是△ABC的一个外角,
∴∠ACD=∠ABC+∠A,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠E=∠ECD﹣∠EBC=∠ACD﹣∠ABC=∠A=25°.
故选:A.
18.(3分)如图所示,已知△ABC≌△ADE,BC的延长线交DE于F,∠B=∠D=25°,∠ACB=∠AED=105°,∠DAC=10°,则∠DFB为( )
A.40° B.50° C.55° D.60°
解:设AD与BF交于点M,
∵∠ACB=105,
∴∠ACM=180°﹣105°=75°,
∠AMC=180°﹣∠ACM﹣∠DAC=180°﹣75°﹣10°=95°,
∴∠FMD=∠AMC=95°,
∴∠DFB=180°﹣∠D﹣∠FMD=180°﹣95°﹣25°=60°.
故选:D.
19.(3分)已知等腰△ABC中,一条边5cm,另一条边8cm,求这个三角形周长( )
A.18cm B.21cm C.18cm或21cm D.不能确定
解:当腰长为5cm时,三角形的三边分别为5cm,5cm,8cm,5+5>8,能组成三角形,
∴此三角形的周长为5+5+8=18cm.
当腰长为8cm时,三角形的三边分别为8cm,8cm,5cm,5+8>8,能组成三角形,
∴此三角形的周长为8+8+5=21cm.
故三角形的周长为:18cm或21cm.
故选:C.
20.(3分)如图,△ABC中,AB=AC,D、E分别在CA、BA的延长线上,连接BD、CE,且∠D+∠E=180°,若BD=6,则CE的长为( )
A.6 B.5 C.3 D.4.5
解:如图,延长BE使AF=AD,连接CF,
在△ADB和△ACF中,
,
∴△ADB≌△ACF(SAS),
∴∠F=∠D,BD=CF=6,
∵∠D+∠BEC=180°,∠BEC+∠FEC=180°,
∴∠D=∠FEC,
∴∠F=∠FEC,
∴CF=CE=6,
故选:A.
二、解答题(21,22,各8分,23题6分,24题8分,25,26,27各10分)
21.解方程组
(1);
(2).
解:(1),
①×3+②得:17x=34,
解得:x=2,
把x=2代入①得:y=4,
则方程组的解为;
(2)方程组整理得:,
把①代入②得:2x﹣=9,
去分母得:12x﹣x﹣1=54,
解得:x=5,
把x=5代入①得:y=1,
则方程组的解为.
22.解不等式
(1)5(x+2)≥1﹣2(x﹣1);
(2)解不等式组.
解:(1)去括号得,5x+10≥1﹣2x+2,
移项得,5x+2x≥1+2﹣10,
合并同类项得,7x≥﹣7,
系数化为1得,x≥﹣1;
(2),
由①得,x<6,
由②得,x≥1,
故此不等式组的解集为:1≤x<6.
23.如图,方格纸中每个小正方形的边长均为1,线段AB的端点A,B均在小正方形的顶点上,请画出满足下面条件的图形,要求所画图形的各个顶点均在小正方形的顶点上.
(1)在图中画出面积为12的钝角△ABC,且满足∠A是钝角;
(2)请连接顶点,用一条线段将图中△ABC分成面积相等的两部分;
(3)请画出△ABC的高CD.
解:如图,
(1)钝角△ABC即为所求;
(2)线段CE即为所求;
(3)高CD即为所求.
24.如图,AB=AC,BE=CD.
(1)求证:∠B=∠C;
(2)连接AO,若∠1=∠2,不添加任何辅助线,直接写出图中所有的全等三角形.
【解答】(1)证明:∵AB=AC,BE=CD,
∴AB﹣BE=AC﹣CD,
即AE=AD,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠C;
(2)解:图中的全等三角形有△ABD≌△ACE,△AEO≌△ADO,△BEO≌△CDO,△ABO≌△ACO,
理由是:∵在△ABO和△ACO中,
,
∴△ABO≌△ACO(AAS);
由(1)知:△ABD≌△ACE;
∵在△AEO和△ADO中,
,
∴△AEO≌△ADO(SAS);
∵在△BEO和△CDO中,
,
∴△BEO≌△CDO(AAS).
25.(10分)2020年是不寻常的一年,新冠肺炎充斥着我们的生活,病毒无情人有情,很多最美逆行者奔赴疫情的前线,不顾自己的安危令我们感动,哈市雷兵公司奔赴疫情前沿慰问医护人员,欲购进甲,乙两种呼吸机.若购进甲种2台,乙种3台,则共需要成本17000元;若购进甲种3台,乙种1台.则共需要成本15000元.
(1)求甲,乙两种呼吸机每台成本分别为多少元?
(2)该公司决定在成本不超过300000元的前提下购进甲、乙两种呼吸机.若购进乙种台数比甲种台数的3倍还多10台,求最多购进甲种呼吸机多少台?
解:(1)设甲种呼吸机每台成本为x元,乙种呼吸机每台成本为y元,根据题意得:
,解得,
答:甲种呼吸机每台成本为4000元,乙种呼吸机每台成本为3000元.
(2)设购进甲种呼吸机a台,则购进乙种呼吸机(3a+10)台,依题意有
4000a+3000(3a+10)≤300000,
解得a≤.
∵a为整数,
∴a最大为20.
故最多购进甲种呼吸机20台.
26.(10分)已知:如图,四边形ABCD中,∠BAD=∠BCD,∠ABC+∠ADC=180°.
(1)如图1,求∠BCD的度数;
(2)如图2,若∠ACB=50°,∠BAE+∠DAC=∠DFC,求∠G的度数;
(3)如图3,在(2)的条件下,若AG=AC,S△ACD:S△ADG=3:7,2∠ADG+∠CDG=180°,DC=5,求DG的长.
解:(1)∵∠BAD=∠BCD,∠ABC+∠ADC=180°,∠BAD+∠BCD+∠ABC+∠ADC=360°,
∴2∠BCD+180°=360°,
∴∠BCD=90°;
(2)由(1)知:∠BAD=∠BCD=90°,
∵∠BAE+∠DAC=∠DFC,∠DFC=∠EFG,
∴∠EFG=∠BAE+∠DAC,
∵∠GEF=∠EAH+∠ACB,
∴∠GEF+∠EFG=∠EAH+∠ACB+∠BAE+∠DAC=∠BAD+∠ACB=90°+50°=140°,
∴∠G=180°﹣140°=40°;
(3)过点A作AM⊥CD,交CD延长线于M,作AN⊥DG于N,如图3所示:
∵2∠ADG+∠CDG=180°,∠ADG+∠ADM+∠CDG=180°,
∴∠ADG=∠ADM,
∴AM=AN,
∵S△ACD=CD?AM,S△ADG=DG?AN,
∴==,
∵S△ACD:S△ADG=3:7,DC=5,
∴=,
∴DG=.
27.(10分)如图.已知在平面直角坐标系中,△ABC的AB边经过原点O,AC交y轴于点D,且D是AC的中点,C(m,0),D(0,n),m.n满足.
(1)如图1,求OC和OD的长度;
(2)如图2,若E是线段CO上的一个动点,当S△AOE=S△AOD时,求E点的坐标;
(3)如图3,在(2)的条件下,若CO平分∠ACB,S△AOC=3S△BOC,求S△BDE.
解:(1)∵m.n满足.
解得,,
∴m=4,n=2,
∴C(4,0),D(0,2),
∴OC=4,OD=2.
(2)如图1,作OM⊥x轴于M,作OH⊥AC于H,
∵D是AC的中点,
∴AD=AC,
∵S△AOD=AD?OH,S△AOC=AC?OH,
∴S△AOD=,
∴S△AOE=S△AOD,
∵S△AOE=EO?AM,S△AOC=OC?AM,
∴OE=OC=×4=2,
∴E(2,0).
(3)如图2,作BQ⊥x轴于Q,作BP⊥y轴于P,延长CB交x轴于点R,
∵CO平分∠ACB,
∴∠DCO=∠BCO,OC=OC,
∵DO⊥OC,
∴∠COD=∠COR=90°,
∴△COD≌△COR(ASA),
∴S△COR=S△COD,OR=OD=2,
由(2)知S△AOD=,即S△COD=S△AOC,
∵S△AOC=3S△BOC,
∴2S△COD=3S△BOC,
∴2S△COD=2×OD?OC=2×4=8,3S△BOC=3×OC?BQ=6BQ,
∴6BQ=8,
∴BQ=,
∴S△BOR=OR?BP=×2PB=PBS△COR﹣S△BOC=4﹣,
∴S△BDE=(S△DOE+S△BOE)﹣S△BOD=()﹣=2.
一、选择题(共20小题).
1.(3分)下列方程中,属于二元一次方程的是( )
A.x+y﹣2=0 B.xy+1=﹣4 C.3x2+y=8 D.x﹣y﹣2z=10
2.(3分)已知a<b,则下列不等式中不正确的是( )
A.2a<2b B.﹣3a<﹣3b C.a+3<b+3 D.a﹣1<b﹣1
3.(3分)在数轴上表示不等式x≥﹣2的解集,正确的是( )
A. B.
C. D.
4.(3分)下列长度的三条线段能组成三角形的是( )
A.1,2,3 B.1,,3 C.3,4,8 D.4,5,6
5.(3分)下列图形不具有稳定性的是( )
A. B.
C. D.
6.(3分)一个多边形的外角和与它的内角和相等,则多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
7.(3分)如图,△ACE≌△DBF,若∠E=∠F,AD=8,BC=2,则AB等于( )
A.6 B.5 C.3 D.不能确定
8.(3分)如图,AD=AC,BD=BC,则△ABC≌△ABD的根据是( )
A.SSS B.ASA C.AAS D.SAS
9.(3分)一只笼子装有鸡和兔共有10个头,34只脚,每只鸡有两只脚,每只兔有四只脚.设鸡有x只,兔有y只,则可列二元一次方程组( )
A. B.
C. D.
10.(3分)下面命题:
(1)二元一次方程2x﹣3y=4的解有且只有一个;
(2)只有一条高在内部的三角形是钝角三角形;
(3)等腰三角形的周长是22,一边是10,那么另一边一定是6;
(4)有两边和一个角分别相等的两个三角形全等;
(5)x=6是x﹣7<0的解集.正确的个数有( )
A.0个 B.1个 C.2个 D.3个
11.(3分)已知4x﹣y=5,用x表示y,得y=( )
A.5﹣4x B.4x﹣5 C. D.
12.(3分)用不等式表示,x与5的差不大于x的2倍( )
A.x﹣5>2x B.x﹣5≥2x C.x﹣5≤2x D.x﹣5<2x
13.(3分)不等式组的整数解为( )
A.2<x≤5 B.5 C.3 D.3,4,5
14.(3分)已知方程组的解满足方程x+2y=k,则k=( )
A.4 B.﹣3 C.3 D.不能确定
15.(3分)如图,∠A=∠D,∠1=∠2,则下面条件中添加后仍不能得到△ABC≌△DEF是( )
A.∠E=∠B B.AF=CD C.AB=ED D.EF=BC
16.(3分)若不等式组的解集为x>2,则a的取值范围是( )
A.a<2 B.a=2 C.a>2 D.a≤2
17.(3分)如图,在△ABC中,∠A=50°,BE平分∠ABC,CE平分∠ACD,则∠E的度数为( )
A.25° B.30° C.50° D.45°
18.(3分)如图所示,已知△ABC≌△ADE,BC的延长线交DE于F,∠B=∠D=25°,∠ACB=∠AED=105°,∠DAC=10°,则∠DFB为( )
A.40° B.50° C.55° D.60°
19.(3分)已知等腰△ABC中,一条边5cm,另一条边8cm,求这个三角形周长( )
A.18cm B.21cm C.18cm或21cm D.不能确定
20.(3分)如图,△ABC中,AB=AC,D、E分别在CA、BA的延长线上,连接BD、CE,且∠D+∠E=180°,若BD=6,则CE的长为( )
A.6 B.5 C.3 D.4.5
二、解答题(21,22,各8分,23题6分,24题8分,25,26,27各10分)
21.解方程组
(1);
(2).
22.解不等式
(1)5(x+2)≥1﹣2(x﹣1);
(2)解不等式组.
23.如图,方格纸中每个小正方形的边长均为1,线段AB的端点A,B均在小正方形的顶点上,请画出满足下面条件的图形,要求所画图形的各个顶点均在小正方形的顶点上.
(1)在图中画出面积为12的钝角△ABC,且满足∠A是钝角;
(2)请连接顶点,用一条线段将图中△ABC分成面积相等的两部分;
(3)请画出△ABC的高CD.
24.如图,AB=AC,BE=CD.
(1)求证:∠B=∠C;
(2)连接AO,若∠1=∠2,不添加任何辅助线,直接写出图中所有的全等三角形.
25.(10分)2020年是不寻常的一年,新冠肺炎充斥着我们的生活,病毒无情人有情,很多最美逆行者奔赴疫情的前线,不顾自己的安危令我们感动,哈市雷兵公司奔赴疫情前沿慰问医护人员,欲购进甲,乙两种呼吸机.若购进甲种2台,乙种3台,则共需要成本17000元;若购进甲种3台,乙种1台.则共需要成本15000元.
(1)求甲,乙两种呼吸机每台成本分别为多少元?
(2)该公司决定在成本不超过300000元的前提下购进甲、乙两种呼吸机.若购进乙种台数比甲种台数的3倍还多10台,求最多购进甲种呼吸机多少台?
26.(10分)已知:如图,四边形ABCD中,∠BAD=∠BCD,∠ABC+∠ADC=180°.
(1)如图1,求∠BCD的度数;
(2)如图2,若∠ACB=50°,∠BAE+∠DAC=∠DFC,求∠G的度数;
(3)如图3,在(2)的条件下,若AG=AC,S△ACD:S△ADG=3:7,2∠ADG+∠CDG=180°,DC=5,求DG的长.
27.(10分)如图.已知在平面直角坐标系中,△ABC的AB边经过原点O,AC交y轴于点D,且D是AC的中点,C(m,0),D(0,n),m.n满足.
(1)如图1,求OC和OD的长度;
(2)如图2,若E是线段CO上的一个动点,当S△AOE=S△AOD时,求E点的坐标;
(3)如图3,在(2)的条件下,若CO平分∠ACB,S△AOC=3S△BOC,求S△BDE.
参考答案
一、选择题(共20小题,每小题3分,满分60分)
1.(3分)下列方程中,属于二元一次方程的是( )
A.x+y﹣2=0 B.xy+1=﹣4 C.3x2+y=8 D.x﹣y﹣2z=10
解:A.x+y﹣2=0是含有两个未知数,且含未知数项的最高次数为一次的整式方程,是二元一次方程;
B.xy+1=﹣4中xy的次数为2,不是二元一次方程;
C.3x2+y=8中3x2的次数为2,不是二元一次方程;
D.x﹣y﹣2z=10中含有3个未知数,不是二元一次方程;
故选:A.
2.(3分)已知a<b,则下列不等式中不正确的是( )
A.2a<2b B.﹣3a<﹣3b C.a+3<b+3 D.a﹣1<b﹣1
解:由a<b得
A. 2a<2b,故选项正确;
B.﹣3a>﹣3b,故选项不正确;
C. a+3<b+3,故选项正确;
D. a﹣1<b﹣1,故选项正确;
故选:B.
3.(3分)在数轴上表示不等式x≥﹣2的解集,正确的是( )
A. B.
C. D.
解:∵不等式x≥﹣2中包含等于号,
∴必须用实心圆点,
∴可排除A、B,
∵不等式x≥﹣2中是大于等于,
∴折线应向右折,
∴可排除D.
故选:C.
4.(3分)下列长度的三条线段能组成三角形的是( )
A.1,2,3 B.1,,3 C.3,4,8 D.4,5,6
解:A、1+2=3,不能组成三角形,故本选项错误;
B、1+<3,不能组成三角形,故本选项错误;
C、3+4<8,不能组成三角形,故本选项错误;
D、4+5>6,能组成三角形,故本选项正确.
故选:D.
5.(3分)下列图形不具有稳定性的是( )
A. B.
C. D.
解:根据三角形的稳定性可得,B、C、D都具有稳定性.不具有稳定性的是A选项.
故选:A.
6.(3分)一个多边形的外角和与它的内角和相等,则多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
解:设多边形的边数为n.
根据题意得:(n﹣2)×180°=360°,
解得:n=4.
故选:B.
7.(3分)如图,△ACE≌△DBF,若∠E=∠F,AD=8,BC=2,则AB等于( )
A.6 B.5 C.3 D.不能确定
解:∵△ACE≌△DBF,∠E=∠F,AD=8,BC=2
∴AC=BD,即AB+BC=CD+BC
∴AB=CD
∴AB=(AD﹣BC)÷2=(8﹣2)÷2=3
故选:C.
8.(3分)如图,AD=AC,BD=BC,则△ABC≌△ABD的根据是( )
A.SSS B.ASA C.AAS D.SAS
解:在△ABC和ABD中,,
∴△ABC≌△ABD(SSS),
故选:A.
9.(3分)一只笼子装有鸡和兔共有10个头,34只脚,每只鸡有两只脚,每只兔有四只脚.设鸡有x只,兔有y只,则可列二元一次方程组( )
A. B.
C. D.
解:设鸡有x只,兔有y只,
依题意得.
故选:A.
10.(3分)下面命题:
(1)二元一次方程2x﹣3y=4的解有且只有一个;
(2)只有一条高在内部的三角形是钝角三角形;
(3)等腰三角形的周长是22,一边是10,那么另一边一定是6;
(4)有两边和一个角分别相等的两个三角形全等;
(5)x=6是x﹣7<0的解集.正确的个数有( )
A.0个 B.1个 C.2个 D.3个
解:(1)二元一次方程2x﹣3y=4的解有无数个,原命题是假命题;
(2)只有一条高在内部的三角形是直角三角形或钝角三角形,是假命题;
(3)等腰三角形的周长是22,一边是10,那么另一边是6或2,是假命题;
(4)有两边和其夹角分别相等的两个三角形全等,原命题是假命题;
(5)x=6是x﹣7<0的解,原命题是假命题;
故选:A.
11.(3分)已知4x﹣y=5,用x表示y,得y=( )
A.5﹣4x B.4x﹣5 C. D.
解:方程4x﹣y=5,
移项得:﹣y=5﹣4x,
解得:y=4x﹣5.
故选:B.
12.(3分)用不等式表示,x与5的差不大于x的2倍( )
A.x﹣5>2x B.x﹣5≥2x C.x﹣5≤2x D.x﹣5<2x
解:由题意得:x﹣5≤2x;
故选:C.
13.(3分)不等式组的整数解为( )
A.2<x≤5 B.5 C.3 D.3,4,5
解:,
由①得:x>2,
由②得:x≤5,
∴不等式组的解集是2<x≤5,
∴不等式组的整数解是3,4,5.
故选:D.
14.(3分)已知方程组的解满足方程x+2y=k,则k=( )
A.4 B.﹣3 C.3 D.不能确定
解:,
①+②得:3x=9,
解得:x=3,
把x=3代入②得;y=﹣3,
则k=x+2y=3﹣6=﹣3.
故选:B.
15.(3分)如图,∠A=∠D,∠1=∠2,则下面条件中添加后仍不能得到△ABC≌△DEF是( )
A.∠E=∠B B.AF=CD C.AB=ED D.EF=BC
解:A、根据∠A=∠D,∠1=∠2和∠E=∠B不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项符合题意;
B、∵AF=CD,
∴AF+FC=CD+FC,
即AC=DF,
在△ABC和△DEF中
∴△ABC≌△DEF(ASA),故本选项不符合题意;
C、在△ABC和△DEF中
∴△ABC≌△DEF(AAS),故本选项不符合题意;
D、在△ABC和△DEF中
∴△ABC≌△DEF(AAS),故本选项不符合题意;
故选:A.
16.(3分)若不等式组的解集为x>2,则a的取值范围是( )
A.a<2 B.a=2 C.a>2 D.a≤2
解:因为不等式组的解集为x>2,根据同大取大的原则可知2≥a,故选D.
17.(3分)如图,在△ABC中,∠A=50°,BE平分∠ABC,CE平分∠ACD,则∠E的度数为( )
A.25° B.30° C.50° D.45°
解:∵∠ACD是△ABC的一个外角,
∴∠ACD=∠ABC+∠A,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠E=∠ECD﹣∠EBC=∠ACD﹣∠ABC=∠A=25°.
故选:A.
18.(3分)如图所示,已知△ABC≌△ADE,BC的延长线交DE于F,∠B=∠D=25°,∠ACB=∠AED=105°,∠DAC=10°,则∠DFB为( )
A.40° B.50° C.55° D.60°
解:设AD与BF交于点M,
∵∠ACB=105,
∴∠ACM=180°﹣105°=75°,
∠AMC=180°﹣∠ACM﹣∠DAC=180°﹣75°﹣10°=95°,
∴∠FMD=∠AMC=95°,
∴∠DFB=180°﹣∠D﹣∠FMD=180°﹣95°﹣25°=60°.
故选:D.
19.(3分)已知等腰△ABC中,一条边5cm,另一条边8cm,求这个三角形周长( )
A.18cm B.21cm C.18cm或21cm D.不能确定
解:当腰长为5cm时,三角形的三边分别为5cm,5cm,8cm,5+5>8,能组成三角形,
∴此三角形的周长为5+5+8=18cm.
当腰长为8cm时,三角形的三边分别为8cm,8cm,5cm,5+8>8,能组成三角形,
∴此三角形的周长为8+8+5=21cm.
故三角形的周长为:18cm或21cm.
故选:C.
20.(3分)如图,△ABC中,AB=AC,D、E分别在CA、BA的延长线上,连接BD、CE,且∠D+∠E=180°,若BD=6,则CE的长为( )
A.6 B.5 C.3 D.4.5
解:如图,延长BE使AF=AD,连接CF,
在△ADB和△ACF中,
,
∴△ADB≌△ACF(SAS),
∴∠F=∠D,BD=CF=6,
∵∠D+∠BEC=180°,∠BEC+∠FEC=180°,
∴∠D=∠FEC,
∴∠F=∠FEC,
∴CF=CE=6,
故选:A.
二、解答题(21,22,各8分,23题6分,24题8分,25,26,27各10分)
21.解方程组
(1);
(2).
解:(1),
①×3+②得:17x=34,
解得:x=2,
把x=2代入①得:y=4,
则方程组的解为;
(2)方程组整理得:,
把①代入②得:2x﹣=9,
去分母得:12x﹣x﹣1=54,
解得:x=5,
把x=5代入①得:y=1,
则方程组的解为.
22.解不等式
(1)5(x+2)≥1﹣2(x﹣1);
(2)解不等式组.
解:(1)去括号得,5x+10≥1﹣2x+2,
移项得,5x+2x≥1+2﹣10,
合并同类项得,7x≥﹣7,
系数化为1得,x≥﹣1;
(2),
由①得,x<6,
由②得,x≥1,
故此不等式组的解集为:1≤x<6.
23.如图,方格纸中每个小正方形的边长均为1,线段AB的端点A,B均在小正方形的顶点上,请画出满足下面条件的图形,要求所画图形的各个顶点均在小正方形的顶点上.
(1)在图中画出面积为12的钝角△ABC,且满足∠A是钝角;
(2)请连接顶点,用一条线段将图中△ABC分成面积相等的两部分;
(3)请画出△ABC的高CD.
解:如图,
(1)钝角△ABC即为所求;
(2)线段CE即为所求;
(3)高CD即为所求.
24.如图,AB=AC,BE=CD.
(1)求证:∠B=∠C;
(2)连接AO,若∠1=∠2,不添加任何辅助线,直接写出图中所有的全等三角形.
【解答】(1)证明:∵AB=AC,BE=CD,
∴AB﹣BE=AC﹣CD,
即AE=AD,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠C;
(2)解:图中的全等三角形有△ABD≌△ACE,△AEO≌△ADO,△BEO≌△CDO,△ABO≌△ACO,
理由是:∵在△ABO和△ACO中,
,
∴△ABO≌△ACO(AAS);
由(1)知:△ABD≌△ACE;
∵在△AEO和△ADO中,
,
∴△AEO≌△ADO(SAS);
∵在△BEO和△CDO中,
,
∴△BEO≌△CDO(AAS).
25.(10分)2020年是不寻常的一年,新冠肺炎充斥着我们的生活,病毒无情人有情,很多最美逆行者奔赴疫情的前线,不顾自己的安危令我们感动,哈市雷兵公司奔赴疫情前沿慰问医护人员,欲购进甲,乙两种呼吸机.若购进甲种2台,乙种3台,则共需要成本17000元;若购进甲种3台,乙种1台.则共需要成本15000元.
(1)求甲,乙两种呼吸机每台成本分别为多少元?
(2)该公司决定在成本不超过300000元的前提下购进甲、乙两种呼吸机.若购进乙种台数比甲种台数的3倍还多10台,求最多购进甲种呼吸机多少台?
解:(1)设甲种呼吸机每台成本为x元,乙种呼吸机每台成本为y元,根据题意得:
,解得,
答:甲种呼吸机每台成本为4000元,乙种呼吸机每台成本为3000元.
(2)设购进甲种呼吸机a台,则购进乙种呼吸机(3a+10)台,依题意有
4000a+3000(3a+10)≤300000,
解得a≤.
∵a为整数,
∴a最大为20.
故最多购进甲种呼吸机20台.
26.(10分)已知:如图,四边形ABCD中,∠BAD=∠BCD,∠ABC+∠ADC=180°.
(1)如图1,求∠BCD的度数;
(2)如图2,若∠ACB=50°,∠BAE+∠DAC=∠DFC,求∠G的度数;
(3)如图3,在(2)的条件下,若AG=AC,S△ACD:S△ADG=3:7,2∠ADG+∠CDG=180°,DC=5,求DG的长.
解:(1)∵∠BAD=∠BCD,∠ABC+∠ADC=180°,∠BAD+∠BCD+∠ABC+∠ADC=360°,
∴2∠BCD+180°=360°,
∴∠BCD=90°;
(2)由(1)知:∠BAD=∠BCD=90°,
∵∠BAE+∠DAC=∠DFC,∠DFC=∠EFG,
∴∠EFG=∠BAE+∠DAC,
∵∠GEF=∠EAH+∠ACB,
∴∠GEF+∠EFG=∠EAH+∠ACB+∠BAE+∠DAC=∠BAD+∠ACB=90°+50°=140°,
∴∠G=180°﹣140°=40°;
(3)过点A作AM⊥CD,交CD延长线于M,作AN⊥DG于N,如图3所示:
∵2∠ADG+∠CDG=180°,∠ADG+∠ADM+∠CDG=180°,
∴∠ADG=∠ADM,
∴AM=AN,
∵S△ACD=CD?AM,S△ADG=DG?AN,
∴==,
∵S△ACD:S△ADG=3:7,DC=5,
∴=,
∴DG=.
27.(10分)如图.已知在平面直角坐标系中,△ABC的AB边经过原点O,AC交y轴于点D,且D是AC的中点,C(m,0),D(0,n),m.n满足.
(1)如图1,求OC和OD的长度;
(2)如图2,若E是线段CO上的一个动点,当S△AOE=S△AOD时,求E点的坐标;
(3)如图3,在(2)的条件下,若CO平分∠ACB,S△AOC=3S△BOC,求S△BDE.
解:(1)∵m.n满足.
解得,,
∴m=4,n=2,
∴C(4,0),D(0,2),
∴OC=4,OD=2.
(2)如图1,作OM⊥x轴于M,作OH⊥AC于H,
∵D是AC的中点,
∴AD=AC,
∵S△AOD=AD?OH,S△AOC=AC?OH,
∴S△AOD=,
∴S△AOE=S△AOD,
∵S△AOE=EO?AM,S△AOC=OC?AM,
∴OE=OC=×4=2,
∴E(2,0).
(3)如图2,作BQ⊥x轴于Q,作BP⊥y轴于P,延长CB交x轴于点R,
∵CO平分∠ACB,
∴∠DCO=∠BCO,OC=OC,
∵DO⊥OC,
∴∠COD=∠COR=90°,
∴△COD≌△COR(ASA),
∴S△COR=S△COD,OR=OD=2,
由(2)知S△AOD=,即S△COD=S△AOC,
∵S△AOC=3S△BOC,
∴2S△COD=3S△BOC,
∴2S△COD=2×OD?OC=2×4=8,3S△BOC=3×OC?BQ=6BQ,
∴6BQ=8,
∴BQ=,
∴S△BOR=OR?BP=×2PB=PBS△COR﹣S△BOC=4﹣,
∴S△BDE=(S△DOE+S△BOE)﹣S△BOD=()﹣=2.
同课章节目录
